机器学习 线性回归 python 和 matlab 版本
线性回归
线性回归是回归问题中最简单的形式,线性回归假设目标值(datay)与特征(datax)之间线性相关,即满足一个多元一次方程(因为影响目标值的特征往往有多个,所以称为多元,此时也称之为多元线性回归)。
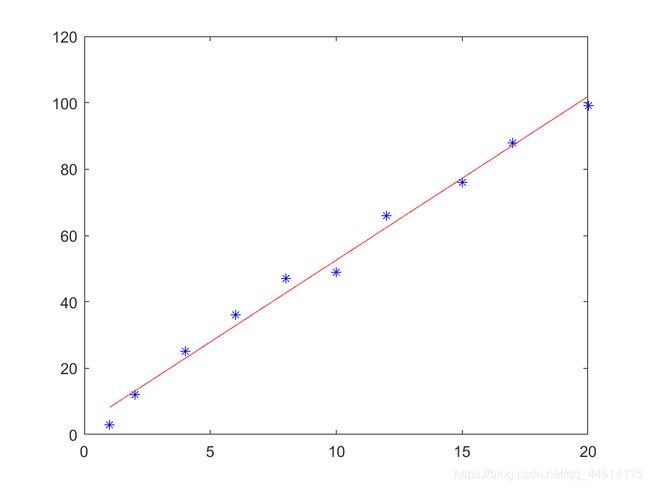
我们可以认为目标值与特征值之间存在以下关系(y 与 x 均可为向量形式),如下图所示,这便是一个比较简单的线性回归,这里y是连续数值型变量
y ^ = w x ^ + b \hat{y} = w\hat{x}+b y^=wx^+b
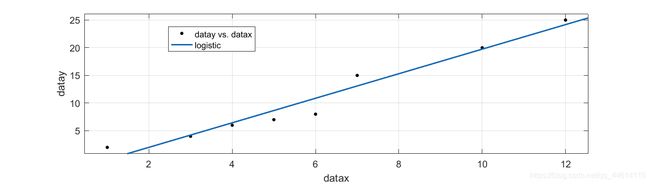
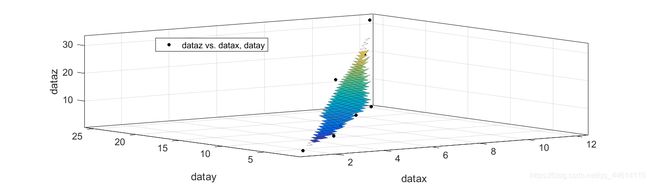
如果是有两个特征值那么x 便是一个二维向量,上图中的直线也会变成一个平面
模型的求解便是对w以及b的求解,只有这两个参数越精确,模型才会越好。表征模型的好坏便是模型的预测值与真实值之间的差距大小。为此,我们定义了损失函数,在回归中我们常称之为残差平方和
1 n ∑ i = 1 n ( y ^ i − y i ) 2 \frac{1}{n}\sum_{i=1}^{n}(\hat{y}_{i} - y_{i})^2 n1i=1∑n(y^i−yi)2
也就是预测值与真实值之间距离平方的平均值
求解模型的过程也就是将损失函数最小化的过程,最终得到w和b
线性回归求解方法
最小二乘法
我们将上述的两个公式结合得到残差平方和与w和b之间的联系
L ( w , b ) = 1 n ∑ i = 1 n ( w x i + b − y i ) 2 L(w,b) = \frac{1}{n} \sum_{i=1}^{n}(w x_{i} + b -y_{i})^2 L(w,b)=n1i=1∑n(wxi+b−yi)2
我们接着进行求导,结合我们高数的知识,最终得到 w 和 b
梯度下降
大致思路为根据每个自变量对损失函数的偏导来更新参数,这里不深探讨
代码实现
matlab
[b,bint,r,rint,stats] = regress(y,X)
| 参数 | 描述 |
|---|---|
| b | 向量 y 中的响应对矩阵 X 中的预测变量的多元线性回归的系数估计值 |
| bint | 返回系数估计值的 95% 置信区间的矩阵 |
| r | 返回由残差组成的向量 |
| rint | 包含可用于诊断离群值的区间 |
| stats | 包含 R2 统计量、F 统计量及其 p 值,以及误差方差的估计值。矩阵 X 必须包含一个由 1 组成的列,以便软件正确计算模型统计量 |
在调用函数的时候需要在矩阵 X 中包含一个由 1 构成的列
x=[1 2 4 6 8 10 12 15 17 20]';
X=[ones(10,1),x];
Y=[3 12 25 36 47 49 66 76 88 99]';
[b,bint,r,rint,stats]=regress(Y,X)
X_Test = linspace(1,20,100);
Y_predict = b(2) * X_Test + b(1);
plot(x,Y, 'b*');
hold on
plot(X_Test,Y_predict,'r-');
python
sklearn包内部自动实现了线性模型的预测,下面实现了简单的线性回归
# 回归分析
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import linear_model
import numpy as np
x = np.array([1, 2, 4, 6, 8, 10, 12, 15, 17, 20])
Y = np.array([3, 12, 25, 36, 47, 49, 66, 76, 88, 99])
# 选取训练集
dataX_train = x
dataY_train = Y
x_test = np.array(np.linspace(1, 20, 100))
print(x_test)
print('实例化模型:')
model_reg = linear_model.LinearRegression()
print("训练模型:")
model_reg.fit(dataX_train.reshape((-1, 1)), dataY_train)
print("模型预测:")
dataY_predict = model_reg.predict(x_test.reshape((-1, 1)))
plt.scatter(dataX_train, dataY_train)
plt.scatter(x_test, dataY_predict)
plt.show()