支持向量机算法
支持向量机算法
SVM算法和感知机,逻辑回归一样,都是经典的二分类算法。其中,支持向量机找到的分割超平面具有更好的鲁棒性,因而被广泛使用在了很多任务上。
一、常见的几何性质(欧氏空间)
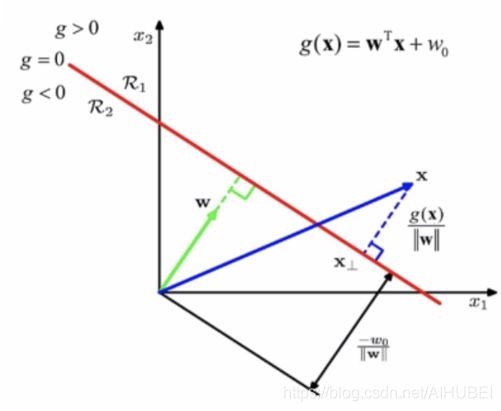
{ w T x 1 + b = 0 w T x 2 + b = 0 w 为 法 向 量 w T ( x 1 − x 2 ) = 0 (式1) \begin{cases} w^Tx_1+b=0\\ w^Tx_2+b=0{\qquad{w为法向量}}\\ w^T(x_1-x_2)=0 \end{cases}\tag{式1} ⎩⎪⎨⎪⎧wTx1+b=0wTx2+b=0w为法向量wT(x1−x2)=0(式1)
{ w T x 1 + b = 0 λ w T w ∣ ∣ w ∣ ∣ + b = 0 − b ∣ ∣ w ∣ ∣ 为 原 点 到 平 面 的 距 离 o f f s e t = − b ∣ ∣ w ∣ ∣ (式2) \begin{cases} w^Tx_1+b=0\\ \lambda{w^T}\cfrac{w}{\vert\vert{w}\vert\vert}+b=0{\qquad{\cfrac{-b}{\vert\vert{w}\vert\vert}}为原点到平面的距离}\\ offset\qquad=\cfrac{-b}{\vert\vert{w}\vert\vert} \end{cases}\tag{式2} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧wTx1+b=0λwT∣∣w∣∣w+b=0∣∣w∣∣−b为原点到平面的距离offset=∣∣w∣∣−b(式2)
r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r 为 点 到 平 面 的 距 离 (式3) r=\cfrac{\vert{w^Tx+b}\vert}{\vert\vert{w}\vert\vert}\qquad{r为点到平面的距离}\tag{式3} r=∣∣w∣∣∣wTx+b∣r为点到平面的距离(式3)
推导如下:
r = ∣ ∣ w T x ∣ ∣ w ∣ ∣ 2 w − − b ∣ ∣ w ∣ ∣ 2 w ∣ ∣ r=\vert\vert{\cfrac{w^Tx}{\vert\vert{w}\vert\vert^2}w-\cfrac{-b}{\vert\vert{w}\vert\vert^2}w}\vert\vert\\ r=∣∣∣∣w∣∣2wTxw−∣∣w∣∣2−bw∣∣
= ∣ ∣ w T x ∣ ∣ w ∣ ∣ 2 + − b ∣ ∣ w ∣ ∣ 2 ∣ ∣ ∣ ∣ w ∣ ∣ =\vert\vert{\cfrac{w^Tx}{\vert\vert{w}\vert\vert^2}+\cfrac{-b}{\vert\vert{w}\vert\vert^2}}\vert\vert\quad{\vert\vert{w}\vert\vert}\\ =∣∣∣∣w∣∣2wTx+∣∣w∣∣2−b∣∣∣∣w∣∣
= ∣ ∣ w T x + b ∣ ∣ ∣ ∣ w ∣ ∣ = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ (式4) =\cfrac{\vert\vert{w^Tx+b}\vert\vert}{\vert\vert{w}\vert\vert}=\cfrac{\vert{w^Tx+b}\vert}{\vert\vert{w}\vert\vert}\tag{式4} =∣∣w∣∣∣∣wTx+b∣∣=∣∣w∣∣∣wTx+b∣(式4)
2、SVM原始形式的导出(核心是最大化间隔)
如图所示:

给定一个二分类器数据集 D = { ( x ( n ) , y ( n ) ) } n = 1 N \mathcal{D}=\{(\boldsymbol{x}^{(n)},y^{(n)})\}_{n=1}^N D={ (x(n),y(n))}n=1N,其中, y n ∈ { + 1 , − 1 } y_n\in\{+1,-1\} yn∈{ +1,−1},如若两类样本线性可分,即存在一个超平面:
w T x + b = 0 (式5) \boldsymbol{w}^T\boldsymbol{x}+b=0\tag{式5} wTx+b=0(式5)
将两类样本分开,那么对于每个样本都有 y ( n ) ( w T x ( n ) + b ) > 0 y^{(n)}(\boldsymbol{w}^T\boldsymbol{x}^{(n)}+b)>0 y(n)(wTx(n)+b)>0.
数据集 D \mathcal{D} D中每个样本 x ( n ) \boldsymbol{x}^{(n)} x(n)到分割超平面的距离为:
r ( n ) = ∣ ∣ w T x ( n ) + b ∣ ∣ ∣ ∣ w ∣ ∣ = y ( n ) ( w T x ( n ) + b ) ∣ ∣ w ∣ ∣ (式6) r^{(n)}=\cfrac{\vert\vert{\boldsymbol{w}^T\boldsymbol{x}^{(n)}+b}\vert\vert}{\vert\vert{\boldsymbol{w}}\vert\vert} =\cfrac{y^{(n)}(\boldsymbol{w}^T\boldsymbol{x}^{(n)}+b)}{\vert\vert\boldsymbol{w}\vert\vert}\tag{式6} r(n)=∣∣w∣∣∣∣wTx(n)+b∣∣=∣∣w∣∣y(n)(wTx(n)+b)(式6)
定义间隔 r r r为整个数据集 D \mathcal{D} D中所有样本到分割超平面的最短距离:
r = min n r ( n ) . (式7) r=\min\limits_{n}r^{(n)}.\tag{式7} r=nminr(n).(式7)
如若间隔 r r r越大,则分割超平面对两个数据集的划分越稳定,不容易受到噪声等因素的影响。支持向量机的目标为:找到一个超平面 ( w ∗ , b ∗ ) (\boldsymbol{w}^*,b^*) (w∗,b∗)使得 r r r最大,即:
max w , b r s . t . y ( n ) ( w T x ( n ) + b ) ∣ ∣ w ∣ ∣ ≥ r , ∀ n ∈ { 1 , ⋯ , N } (式8) \max\limits_{\boldsymbol{w},b}\qquad{r}\\ s.t.\qquad{\cfrac{y^{(n)}(\boldsymbol{w}^T\boldsymbol{x}^{(n)}+b)}{\vert\vert{\boldsymbol{w}}\vert\vert}}\ge{r},\forall_n\in\{1,\cdots,N\}\tag{式8} w,bmaxrs.t.∣∣w∣∣y(n)(wTx(n)+b)≥r,∀n∈{ 1,⋯,N}(式8)
因为间隔为 r = 1 ∣ ∣ w ∣ ∣ r=\cfrac{1}{\vert\vert{\boldsymbol{w}}\vert\vert} r=∣∣w∣∣1,令 ∣ ∣ w ∣ ∣ ⋅ r = 1 \vert\vert\boldsymbol{w}\vert\vert\cdot{r}=1 ∣∣w∣∣⋅r=1,则 ( 式 8 ) (式8) (式8)等价于:
max w , b 1 ∣ ∣ w ∣ ∣ 2 s . t . y ( n ) ( w T x ( n ) + b ) ≥ 1 , ∀ n ∈ { 1 , ⋯ , N } (式9) \max\limits_{\boldsymbol{w},b}\qquad{\cfrac{1}{\vert\vert{\boldsymbol{w}}\vert\vert^2}}\\ s.t.\qquad{ {y^{(n)}(\boldsymbol{w}^T\boldsymbol{x}^{(n)}+b)}}\ge{1},\forall_n\in\{1,\cdots,N\}\tag{式9} w,bmax∣∣w∣∣21s.t.y(n)(wTx(n)+b)≥1,∀n∈{ 1,⋯,N}(式9)
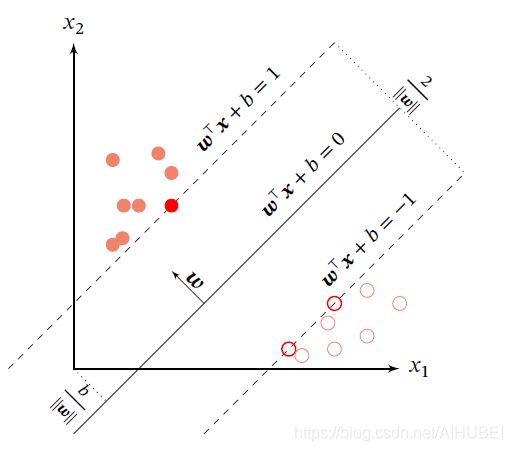
数据集中所有满足 y ( n ) ( w T x ( n ) + b ) = 1 { {y^{(n)}(\boldsymbol{w}^T\boldsymbol{x}^{(n)}+b)}}=1 y(n)(wTx(n)+b)=1的样本点都称之为支持向量。对于一个线性可分的数据集,其分割超平面有很多个,但是间隔最大的超平面是唯一的. 下图给定了支持向量机的最大间隔分割超平面的示例,其中红色样本点为支持向量.
三、SVM参数的学习
将 ( 式 9 ) (式9) (式9)写成凸优化问题,形式如下:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 (式10) \min\limits_{\boldsymbol{w},b} \qquad{\cfrac{1}{2}}{\vert\vert{\boldsymbol{w}}\vert\vert}^2\tag{式10} w,bmin21∣∣w∣∣2(式10)
s . t . 1 − y ( n ) ( w T x + b ) ≤ 0 , ∀ n ∈ { 1 , ⋯ , N } s.t.\qquad{1-y^{(n)}(\boldsymbol{w}^T\boldsymbol{x}+b)}\le0,\qquad{\forall_{n}\in\{1,\cdots,N\}} s.t.1−y(n)(wTx+b)≤0,∀n∈{ 1,⋯,N}
使用拉格朗日乘数法, ( 式 10 ) (式10) (式10)的拉格朗日函数为:
L ( w , b , λ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ n = 1 N λ n ( 1 − y ( n ) ( w T x ( n ) + b ) ) (式11) L(\boldsymbol{w},b,\lambda)=\cfrac{1}{2}{\vert\vert{\boldsymbol{w}}\vert\vert}^2+\sum_{n=1}^{N}\lambda_n(1-y^{(n)}(\boldsymbol{w}^T\boldsymbol{x}^{(n)}+b))\tag{式11} L(w,b,λ)=21∣∣w∣∣2+n=1∑Nλn(1−y(n)(wTx(n)+b))(式11)
其中,拉格朗日乘子 λ ≥ 0 \lambda\ge0 λ≥0,计算 L ( w , b , λ ) L(\boldsymbol{w},b,\lambda) L(w,b,λ)关于 w \boldsymbol{w} w和 b b b的导数,并分别令为零.得到:
w = ∑ n = 1 N λ n y ( n ) x ( n ) (式12) \boldsymbol{w}=\sum_{n=1}^{N}\lambda_ny^{(n)}\boldsymbol{x}^{(n)}\tag{式12} w=n=1∑Nλny(n)x(n)(式12)
0 = ∑ n = 1 N λ n y ( n ) (式13) 0=\sum_{n=1}^{N}\lambda_ny^{(n)}\tag{式13} 0=n=1∑Nλny(n)(式13)
将 ( 式 12 ) (式12) (式12)带入到 ( 式 11 ) (式11) (式11),同时根据 ( 式 13 ) (式13) (式13),得到拉格朗日对偶函数如下:
Γ ( λ ) = − 1 2 ∑ n = 1 N ∑ m = 1 N λ m λ n y ( m ) y ( n ) ( x ( m ) ) T x ( n ) + ∑ n = 1 N λ n (式14) \Gamma(\lambda)=-\cfrac{1}{2}\sum_{n=1}^{N}\sum_{m=1}^{N}\lambda_m\lambda_ny^{(m)}y^{(n)}(\boldsymbol{x}^{(m)})^T\boldsymbol{x}^{(n)}+\sum_{n=1}^{N}\lambda_n \tag{式14} Γ(λ)=−21n=1∑Nm=1∑Nλmλny(m)y(n)(x(m))Tx(n)+n=1∑Nλn(式14)
支持向量机的主优化问题为凸优化问题,满足强对偶性,即主优化问题可以
通过最大化对偶函数 m a x λ ≥ 0 Γ ( λ ) max_{\lambda\ge0}\Gamma(\lambda) maxλ≥0Γ(λ)来求解. 对偶函数 Γ ( λ ) \Gamma(\lambda) Γ(λ)是一个凹函数,因此最大化对偶函数是一个凸优化问题,可以通过多种凸优化方法来进行求解,得到拉格朗日乘数的最优值 λ ∗ \lambda^* λ∗. 但由于其约束条件的数量为训练样本数量,一般的优化方法代价比较高,因此在实践中通常采用比较高效的优化方法,比如序列最小优化.