机器学习——最简单的回归——一元线性回归（基于python3.9和sklearn）

最近学 聚类 学累了 ，学一学高中生都会的一元线性回归吧

高中的时候都学过，从一堆离散的点集提取出一个看起来很符合点分布的曲线。即研究输出关于输入的函数映射关系。回归问题的学习过程等价于拟合过程：选择一条曲线使得其能够较良好地拟合数据点的分布。
高中学的都是一元的，而且是线性的，也就是说得到的贴合的曲线是一条直线，今天就来温习一波

熟悉matlab的朋友可能知道自带的regress函数，而在python中需要用到sklearn库的linear_model.LinearRegression()函数

映射关系：

 一元线性回归最终的形式如下：$\hat{y}=\omega x+b$ ，其中$w$称为权重，$b$称为偏置，$\hat{y}$是$y$的估计值

由这个式子可以看出，$w$和$b$是这个是式子的核心，确定了直线的位置，由于$\hat{y}$是估计值，总是与真实值存在误差，所以引入一个误差函数$Loss$量化这个回归曲线的贴合程度的好坏

误差函数：

                $L=\frac{1}{n}{\sum }_{i=0}^n(\widehat{y_i}-y_i{)}^2$
 其中：$n$为样本总数，$\hat{y}$为模型预测标签， $y$为样本真实标签。上面这种损失函数称为均方损失函数或$L2$损失函数。

解析解：

这张图是我从概率论老师的ppt上扒下来的 QAQ
 图中的$a$对应于权重$w$，$b$对应于偏置$b$
     下面的求偏导的公式很重要，对于理解整个算法起到很重要的作用

（是不是觉得这几个式子很熟悉 QAQ)

梯度下降法：

 学长写的太详细了，不好意思直接扒QAQ，直接给出链接 我没有扒

其他知识点：

参考这篇文章 我是链接

代码：

 先看一波数据是啥样的（单纯的txt文件）txt什么时候才能站起来 QAQ

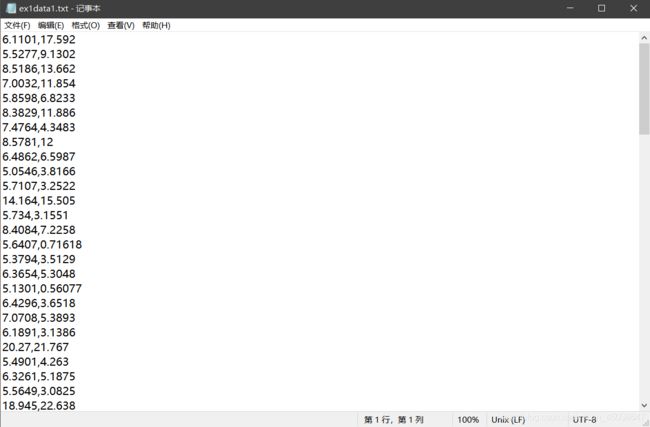
 下面分别是不使用sklearn和使用sklearn的代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score


def load_data(path):
    data = pd.read_csv(path, header=None, names=['population', 'profit'])
    return data, data.head(), data.describe()


def visualization_data(data):
    fig, ax = plt.subplots(figsize=(6, 6))
    ax.scatter(data['population'], data['profit'])
    ax.set_xlabel('population')
    ax.set_ylabel('profit')
    ax.set_title('population vs profit')
    plt.show()


# visualization_data()
def data_preprocessing(data):
    # data.insert(0, 'one', 1)  # 在第0列插入names为'ones' 值为1的列
    col = data.shape[1]  # 列数
    x = data.iloc[:, :col - 1]
    y = data.iloc[:, col - 1:]  # 最后一列 注意 这里变成了列向量
    return x, y


def costfunction(x, y, theta):
    h = x * theta[0, 0] + theta[0, 1]  # 矩阵相乘 x是:*1向量 theta是1*2向量
    temp = np.power((h - y), 2)  # x与theta相乘之后减去y 再做平方
    J = np.sum(temp) / (2 * len(x))  # 平滑操作 这里2是常数 可要可不要
    return J


# print(J)
def gradientdescend(x, y, theta, alpha, num_iter):
    theta_t = np.array(np.zeros(theta.shape))
    cost = np.zeros(num_iter)
    m = len(x)
    for i in range(num_iter):  # 迭代
        theta_t[0, 0] = theta[0, 0] - (alpha / m) * (theta_t[0, 0] * x.T @ x - (y - theta[0, 1]).T @ x)
        theta_t[0, 1] = theta[0, 1] - (alpha / m) * (m * theta[0, 1] - sum((y - theta[0, 0] * x)))
        theta = theta_t
        cost[i] = costfunction(x, y, theta)  # 记录cost值 便于画出每次迭代的cost值
    return theta, cost


def unuse_sklearn():
    data, data_head, data_describe = load_data('ex1data1.txt')
    x, y = data_preprocessing(data)

    x = np.array(x.values)  # first col
    y = np.array(y.values)  # second col
    theta = np.array([[0, 0]])  # 分别是 权重 偏置
    print('x:', x.shape, 'y:', y.shape, 'theta', theta.shape)

    alpha = 0.01  # 学习率
    iterations = 1000  # 迭代次数
    fin_theta, cost = gradientdescend(x, y, theta, alpha, iterations)  # 迭代开始
    fin_cost = costfunction(x, y, fin_theta)
    print('fin_cost', fin_cost)
    print('fin_theta:', fin_theta, "fin_theta's shape:", fin_theta.shape)

    J = costfunction(x, y, theta)

    x = np.linspace(data.population.min(), data.population.max(), 200)
    f = fin_theta[0, 1] + (fin_theta[0, 0] * x)
    fig, ax = plt.subplots(figsize=(8, 8))
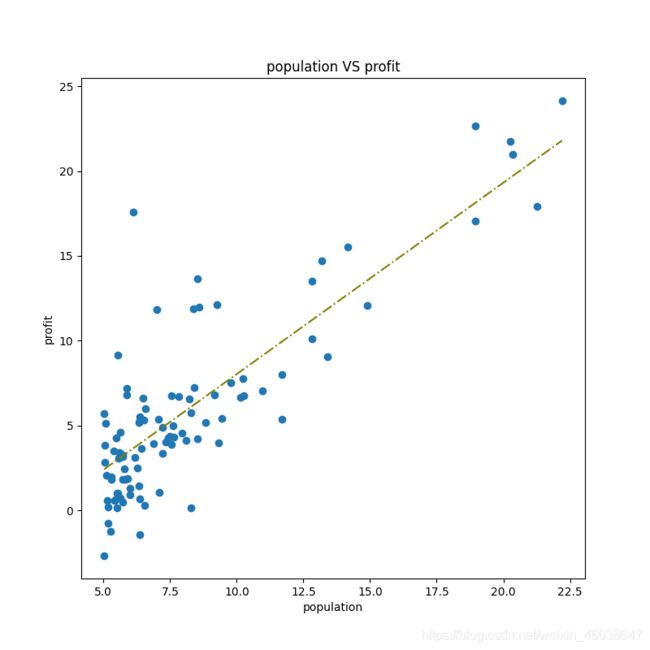
    ax.plot(x, f, 'olive', label='result of prediction', linestyle='-.')
    ax.scatter(data['population'], data['profit'])
    ax.set_xlabel('population')
    ax.set_ylabel('profit')
    ax.set_title('population VS profit')
    plt.show()

    fig, ax = plt.subplots(figsize=(6, 6))
    ax.plot(np.arange(iterations), cost, 'r')
    ax.set_xlabel('iterations')
    ax.set_ylabel('costfunction')
    ax.set_title('iterations VS costfunction')
    plt.show()


def use_sklearn():
    # Load the diabetes dataset
    diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)

    # Use only one feature
    diabetes_X = diabetes_X[:, np.newaxis, 2]

    # Split the data into training/testing sets
    diabetes_X_train = diabetes_X[:-20]
    diabetes_X_test = diabetes_X[-20:]

    # Split the targets into training/testing sets
    diabetes_y_train = diabetes_y[:-20]
    diabetes_y_test = diabetes_y[-20:]

    # Create linear regression object
    regr = linear_model.LinearRegression()

    # Train the model using the training sets
    regr.fit(diabetes_X_train, diabetes_y_train)

    # Make predictions using the testing set
    diabetes_y_pred = regr.predict(diabetes_X_test)

    # The coefficients
    print('Coefficients: \n', regr.coef_)
    # The mean squared error
    print('Mean squared error: %.2f'
          % mean_squared_error(diabetes_y_test, diabetes_y_pred))
    # The coefficient of determination: 1 is perfect prediction
    print('Coefficient of determination: %.2f'
          % r2_score(diabetes_y_test, diabetes_y_pred))

    # Plot outputs
    plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
    plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)

    plt.xticks(())
    plt.yticks(())

    plt.show()


unuse_sklearn()
use_sklearn()

运行结果：