本文是机器学习系列的第三篇,算上前置机器学习系列是第八篇。本文的概念相对简单,主要侧重于代码实践。
上一篇文章说到,我们可以用线性回归做预测,但显然现实生活中不止有预测的问题还有分类的问题。我们可以从预测值的类型上简单区分:连续变量的预测为回归,离散变量的预测为分类。
一、逻辑回归:二分类
1.1 理解逻辑回归
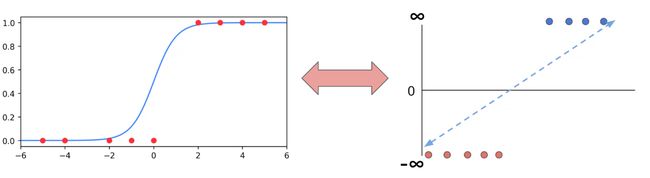
我们把连续的预测值进行人工定义,边界的一边定义为1,另一边定义为0。这样我们就把回归问题转换成了分类问题。
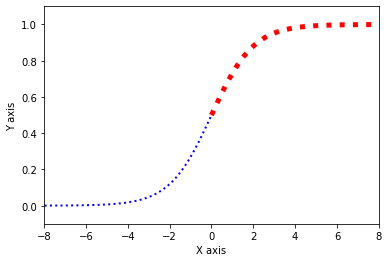
如上图,我们把连续的变量分布压制在0-1的范围内,并以0.5作为我们分类决策的边界,大于0.5的概率则判别为1,小于0.5的概率则判别为0。
我们无法使用无穷大和负无穷大进行算术运算,我们通过逻辑回归函数(Sigmoid函数/S型函数/Logistic函数)可以讲数值计算限定在0-1之间。
$$ \sigma(x) = \frac{1}{1+e^{-x}} $$
以上就是逻辑回归的简单解释。下面我们应用真实的数据案例来进行二分类代码实践。
1.2 代码实践 - 导入数据集
添加引用:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt导入数据集(大家不用在意这个域名):
df = pd.read_csv('https://blog.caiyongji.com/assets/hearing_test.csv')
df.head()| age | physical_score | test_result |
|---|---|---|
| 33 | 40.7 | 1 |
| 50 | 37.2 | 1 |
| 52 | 24.7 | 0 |
| 56 | 31 | 0 |
| 35 | 42.9 | 1 |
该数据集,对5000名参与者进行了一项实验,以研究年龄和身体健康对听力损失的影响,尤其是听高音的能力。此数据显示了研究结果对参与者进行了身体能力的评估和评分,然后必须进行音频测试(通过/不通过),以评估他们听到高频的能力。
- 特征:1. 年龄 2. 健康得分
- 标签:(1通过/0不通过)
1.3 观察数据
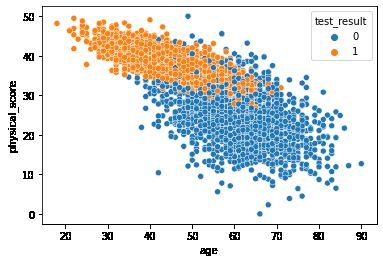
sns.scatterplot(x='age',y='physical_score',data=df,hue='test_result')我们用seaborn绘制年龄和健康得分特征对应测试结果的散点图。
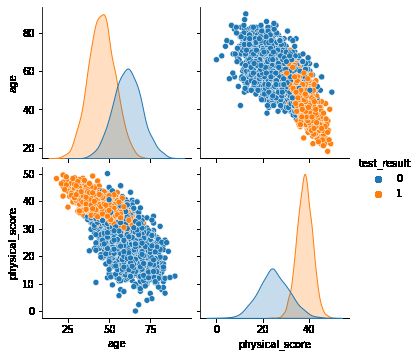
sns.pairplot(df,hue='test_result')我们通过pairplot方法绘制特征两两之间的对应关系。
我们可以大致做出判断,当年龄超过60很难通过测试,通过测试者普遍健康得分超过30。
1.4 训练模型
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score,classification_report,plot_confusion_matrix
#准备数据
X = df.drop('test_result',axis=1)
y = df['test_result']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=50)
scaler = StandardScaler()
scaled_X_train = scaler.fit_transform(X_train)
scaled_X_test = scaler.transform(X_test)
#定义模型
log_model = LogisticRegression()
#训练模型
log_model.fit(scaled_X_train,y_train)
#预测数据
y_pred = log_model.predict(scaled_X_test)
accuracy_score(y_test,y_pred)我们经过准备数据,定义模型为LogisticRegression逻辑回归模型,通过fit方法拟合训练数据,最后通过predict方法进行预测。
最终我们调用accuracy_score方法得到模型的准确率为92.2%。
二、模型性能评估:准确率、精确度、召回率
我们是如何得到准确率是92.2%的呢?我们调用plot_confusion_matrix方法绘制混淆矩阵。
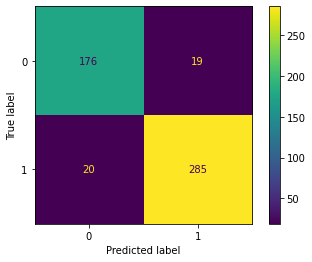
plot_confusion_matrix(log_model,scaled_X_test,y_test)我们观察500个测试实例,得到矩阵如下:
我们对以上矩阵进行定义如下:
- 真正类TP(True Positive) :预测为正,实际结果为正。如,上图右下角285。
- 真负类TN(True Negative) :预测为负,实际结果为负。如,上图左上角176。
- 假正类FP(False Positive) :预测为正,实际结果为负。如,上图左下角19。
- 假负类FN(False Negative) :预测为负,实际结果为正。如,上图右上角20。
准确率(Accuracy) 公式如下:
$$ Accuracy = \frac{TP+TN}{TP+TN+FP+FN} $$
带入本例得:
$$ Accuracy = \frac{285+176}{285+176+20+19} = 0.922 $$
精确度(Precision) 公式如下:
$$ Precision = \frac{TP}{TP+FP} $$
带入本例得:
$$ Precision = \frac{285}{285+19} = 0.9375 $$
召回率(Recall) 公式如下:
$$ Recall = \frac{TP}{TP+FN} $$
带入本例得:
$$ Recall = \frac{285}{285+20} = 0.934 $$
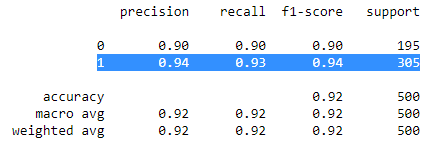
我们调用classification_report方法可验证结果。
print(classification_report(y_test,y_pred))三、Softmax:多分类
3.1 理解softmax多元逻辑回归
Logistic回归和Softmax回归都是基于线性回归的分类模型,两者无本质区别,都是从伯努利分结合最大对数似然估计。
最大似然估计:简单来说,最大似然估计就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值。
术语“概率”(probability)和“似然”(likelihood)在英语中经常互换使用,但是它们在统计学中的含义却大不相同。给定具有一些参数θ的统计模型,用“概率”一词描述未来的结果x的合理性(知道参数值θ),而用“似然”一词表示描述在知道结果x之后,一组特定的参数值θ的合理性。
Softmax回归模型首先计算出每个类的分数,然后对这些分数应用softmax函数,估计每个类的概率。我们预测具有最高估计概率的类,简单来说就是找得分最高的类。
3.2 代码实践 - 导入数据集
导入数据集(大家不用在意这个域名):
df = pd.read_csv('https://blog.caiyongji.com/assets/iris.csv')
df.head()| sepal_length | sepal_width | petal_length | petal_width | species |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 4.9 | 3 | 1.4 | 0.2 | setosa |
| 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 3.6 | 1.4 | 0.2 | setosa |
该数据集,包含150个鸢尾花样本数据,数据特征包含花瓣的长度和宽度和萼片的长度和宽度,包含三个属种的鸢尾花,分别是山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)。
- 特征:1. 花萼长度 2. 花萼宽度 3. 花瓣长度 4 花萼宽度
- 标签:种类:山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)
3.3 观察数据
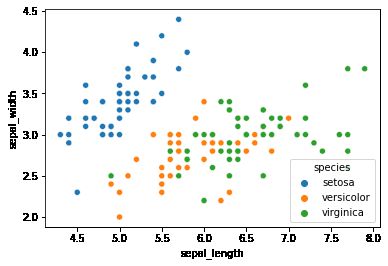
sns.scatterplot(x='sepal_length',y='sepal_width',data=df,hue='species')我们用seaborn绘制花萼长度和宽度特征对应鸢尾花种类的散点图。
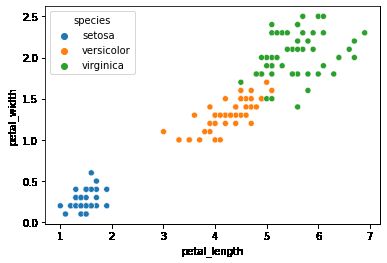
sns.scatterplot(x='petal_length',y='petal_width',data=df,hue='species')我们用seaborn绘制花瓣长度和宽度特征对应鸢尾花种类的散点图。
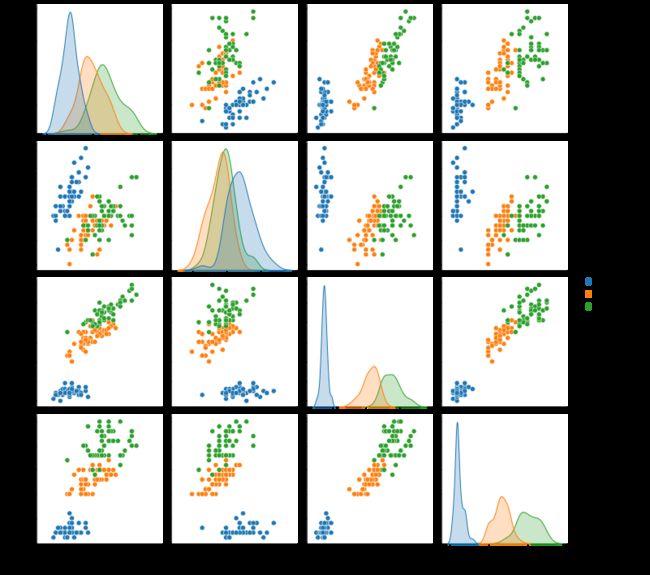
sns.pairplot(df,hue='species')我们通过pairplot方法绘制特征两两之间的对应关系。
我们可以大致做出判断,综合考虑花瓣和花萼尺寸最小的为山鸢尾花,中等尺寸的为变色鸢尾花,尺寸最大的为维吉尼亚鸢尾花。
3.4 训练模型
#准备数据
X = df.drop('species',axis=1)
y = df['species']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=50)
scaler = StandardScaler()
scaled_X_train = scaler.fit_transform(X_train)
scaled_X_test = scaler.transform(X_test)
#定义模型
softmax_model = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=50)
#训练模型
softmax_model.fit(scaled_X_train,y_train)
#预测数据
y_pred = softmax_model.predict(scaled_X_test)
accuracy_score(y_test,y_pred)我们经过准备数据,定义模型LogisticRegression的multi_class="multinomial"多元逻辑回归模型,设置求解器为lbfgs,通过fit方法拟合训练数据,最后通过predict方法进行预测。
最终我们调用accuracy_score方法得到模型的准确率为92.1%。
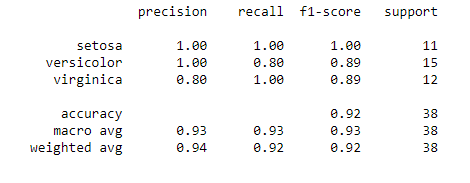
我们调用classification_report方法查看准确率、精确度、召回率。
print(classification_report(y_test,y_pred))3.5 拓展:绘制花瓣分类
我们仅提取花瓣长度和花瓣宽度的特征来绘制鸢尾花的分类图像。
#提取特征
X = df[['petal_length','petal_width']].to_numpy()
y = df["species"].factorize(['setosa', 'versicolor','virginica'])[0]
#定义模型
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=50)
#训练模型
softmax_reg.fit(X, y)
#随机测试数据
x0, x1 = np.meshgrid(
np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
#预测
y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)
#绘制图像
zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])
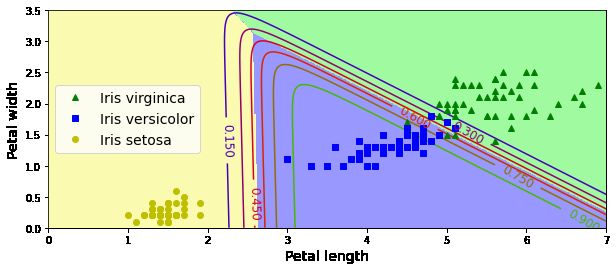
plt.show()得到鸢尾花根据花瓣分类的图像如下:
四、小结
相比于概念的理解,本文更侧重上手实践,通过动手编程你应该有“手热”的感觉了。截至到本文,你应该对机器学习的概念有了一定的掌握,我们简单梳理一下:
- 机器学习的分类
- 机器学习的工业化流程
- 特征、标签、实例、模型的概念
- 过拟合、欠拟合
- 损失函数、最小二乘法
- 梯度下降、学习率
7.线性回归、逻辑回归、多项式回归、逐步回归、岭回归、套索(Lasso)回归、弹性网络(ElasticNet)回归是最常用的回归技术
- Sigmoid函数、Softmax函数、最大似然估计
如果你还有不清楚的地方请参考: