基于C++的带权无向图的实现 (四)- Dijkstra最短路径算法
该系列文章是本人整理的有关带权无向图的数据结构和算法的分析与实现,如有问题或者建议欢迎各位指出。
目录
基于C++的带权无向图的实现 (一)- 数据结构
基于C++的带权无向图的实现 (二)- 遍历算法
基于C++的带权无向图的实现 (三)- Prim最小生成树算法
基于C++的带权无向图的实现 (四)- Dijkstra最短路径算法
最短路径
最短路径问题
在图论中,最短路径问题旨在寻找图中一个顶点到其他顶点的最短路径, 主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。对该问题最直观的理解就是地图导航寻找最短路线。假如我要从广州南站驾车前往广州塔,这里拿高德地图中给出的推荐线路举例:
可以知道,一共有三条路线,其中深绿色这条路线所走的路程最短,仅需要22公里。
对于最短路径问题,常用的算法有:
- 迪杰斯特拉算法(Dijkstra’s Algorithm)
- 弗洛伊德算法(Floyd’s Algorithm)
- SPFA算法 (Bellman-Ford’s Algorithm)
本节内容将对迪杰斯特拉算法进行详解。
Dijkstra算法步骤
给定图G,该图具有非负边权重和起始顶点start。
- 设置对顶点start的距离为0,对图中其他顶点的距离为正无穷。
- 对所有顶点标记为未访问状态。
- 将初始顶点start为u。
- 当图中任有未访问过的顶点时:
- 将当前顶点u设置为已访问状态。
- 对于当前顶点未访问过的邻居顶点v,依次将邻居顶点v到起始顶点start的距离 与(当前顶点u到起始到起始点start的距离 + 当前顶点u到该邻居顶点v的距离)进行比较,并以较小的一个为准。
- 选择具有最小暂定距离的未访问顶点,并将其设置为当前顶点。
此外,遍历顶点需要用到广度优先遍历算法,选择具有最小暂定距离的未访问顶点需要用到优先队列(priority_queue)。
Dijkstra算法图解
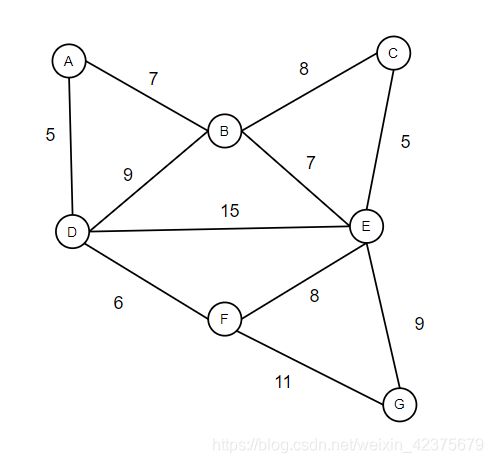
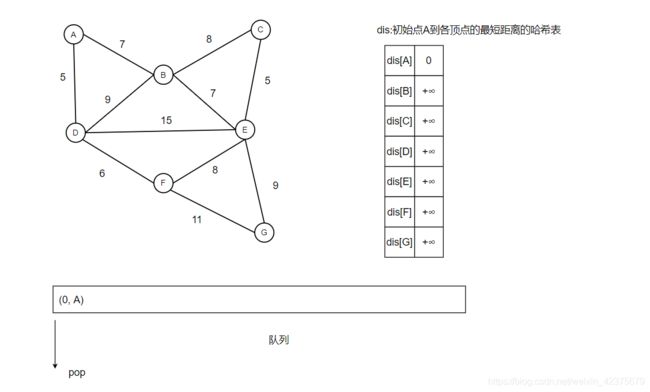
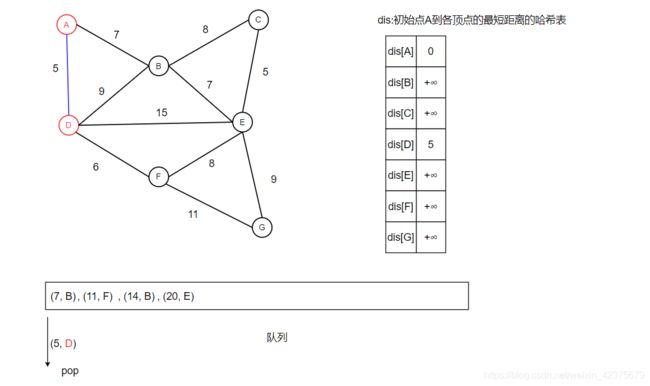
接下来的图中我会使用红色表示该顶点已访问,使用蓝色表示走过的路径,使用哈希表dis表示初始点到图中各个点的最短距离,假设我们从顶点A出发,求顶点A到图中各个顶点的距离,那么初始情况如下所示:
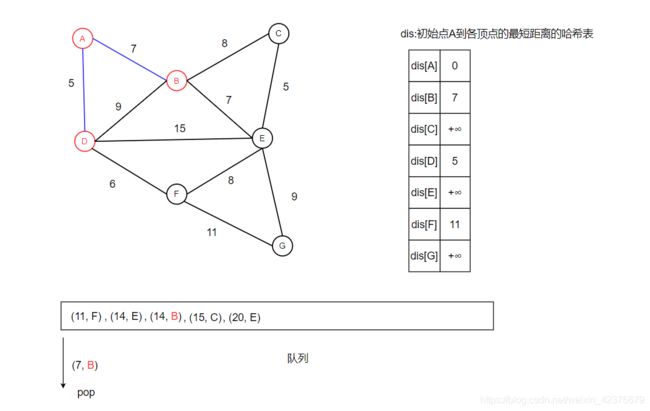
队列首元素出队,如下图所示。由于顶点A尚未访问,因此标记顶点A为已访问。然后遍历顶点A所有未访问过的邻居,将dis[A]加上A点到所有未访问过的邻居的距离依次放入队列中如下所示:
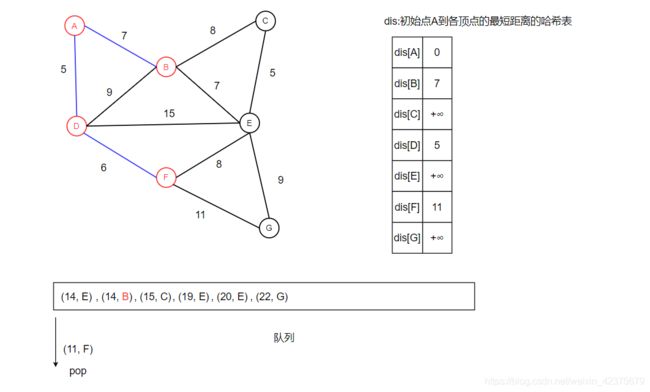
队列首元素出队,如下图所示。由于顶点D尚未访问,因此标记顶点D为已访问。然后遍历顶点D所有未访问过的邻居,将dis[D]加上D点到所有未访问过的邻居的距离依次放入队列后,发现队列中有出现了两个带有未访问顶点B的元素,其所走路径和长度分别为:
- d(A->B) = dis[A] + weight(A , B) = 0 + 7
- d(A->D->B) = dis[D] + weight(D , B) = 5 + 9 = 14
因此选择较小的距离,这里d(A->B)最短,长度为7,所以在队列中这该元素相对靠前。
首元素出队,如下图所示。标记顶点B为已访问,然后遍历顶点B所有未访问过的邻居,将dis[B]加上B点到所有未访问过的邻居的距离依次放入队列中如下所示:
首元素出队,如下图所示。由于顶点F尚未访问,因此标记顶点F为已访问。然后遍历顶点F所有未访问过的邻居,将dis[F]加上F点到所有未访问过的邻居的距离依次放入队列后,发现队列中有出现了三个带有未访问顶点E的元素,其所走路径和长度分别为:
- d(A->B->E) = dis[B] + weight(B , E) = 7 + 7 = 14
- d(A->D->E) = dis[D] + weight(D , E) = 5 + 15 = 20
- d(A->D->F->E) = dis[F] + weight(F , E) = 11 + 8 = 19
因此选择较小的距离,这里d(A->B->E)最短,长度为14,所以在队列中这该元素相对靠前。
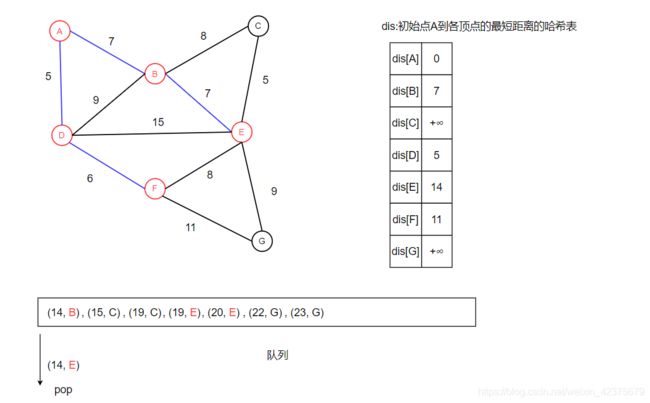
首元素出队,如下图所示。标记顶点E为已访问,然后遍历顶点E所有未访问过的邻居,将dis[E]加上E点到所有未访问过的邻居的距离依次放入队列后,发现队列中出现了两个带有未访问顶点C的元素,其所走路径和长度分别为:
- d(A->B->C) = dis[B] + weight(B , C) = 7+ 8 = 15
- d(A->D->E->C) = dis[E] + weight(E , C) = 14 + 5 = 19
因此选择较小的距离,这里d(A->B->C) 最短,长度为15,所以在队列中这该元素相对靠前。
除此之外,队列中出现了两个带有未访问顶点G的元素,其所走路径和长度分别为:
- d(A->B->E->G) = dis[E] + weight(E , G) = 14 + 9 = 23
- d(A->D->F->G) = dis[F] + weight(F , G) = 11 + 11 = 22
因此选择较小的距离,这里d(A->D->F->G) 最短,长度为22,所以在队列中这该元素相对靠前。
首元素出队,由于顶点B已经访问过,所以跳过,访问顶点C。由于顶点C未访问过,所以标记顶点C为已访问,然后遍历顶点C所有未访问过的邻居,由于顶点C所有邻居已经访问过,所以不会有元素入队,如下所示:
接下来,由于顶点C和E已经访问过,所以都跳过,直到(22,G)出队,如下所示:
代码实现
在Graph类中除了上节内容实现的功能外,额外添加了遍历算法,T为提前定义好的模板:
| 函数名 | 用途 |
|---|---|
| map |
Dijkstra最短路径算法 |
- 边的定义(edge.hpp):
template <typename T>
class Edge {
public:
T vertex;
int weight;
Edge(T neighbour_vertex) {
this->vertex = neighbour_vertex;
this->weight = 0;
}
Edge(T neighbour_vertex, int weight) {
this->vertex = neighbour_vertex;
this->weight = weight;
}
bool operator<(const Edge& obj) const {
return obj.vertex > vertex;
}
bool operator==(const Edge& obj) const {
return obj.vertex == vertex;
}
};
- 图的定义(graph.hpp)
#include由于图的函数声明除了最后一个函数其他的都在前两节中实现了,所以这里只放Dijkstra算法的实现代码(graph.hpp):
template <typename T> map<T,int> Graph<T>::dijkstra(T start) {
// 设置dis用来存放初始点到图中任何一个顶点的距离
map<T, int> dis;
// 设置带权重的队列,按每个pair的第一个元素进行从小到大的排列
priority_queue<pair<int, T>, vector<pair<int, T>>, greater<pair<int, T>>> q;
// 设置初始顶点到自己的距离为0
dis[start] = 0;
// 设置初始顶点到其他顶点的距离为无穷大,这里假定99999为无限大
int infinity = 99999;
for (auto neighbour: adj[start]) {
dis[neighbour.vertex] = infinity;
}
// 设置集合visited来存放已经访问过的顶点
set<T> visited;
// 入队:入队的元素是一个pair类型,第一个值是权重,第二个值是顶点
q.push(make_pair(0,start));
while (!q.empty()) {
// 队首元素出队
auto front = q.top();
q.pop();
// 获得当前顶点
T u = front.second;
// 如果该顶点已经访问过则跳过本此循环,否则存入到集合visited中表示已经访问过
if (visited.find(u) != visited.end()) continue;
else visited.insert(u);
// 获得到顶点u的最短路径"shortest_distance_to_u",将此路径存入到dis结果中
int shortest_distance_to_u = front.first;
dis[u] = shortest_distance_to_u;
// 依次访问顶点u尚未访问过的邻居
for (auto v : adj[u]) {
if (visited.find(v.vertex) == visited.end()) {
// 从顶点u到邻居v的路径记为“distance_to_v”
int distance_to_v = v.weight;
q.push(make_pair(shortest_distance_to_u + distance_to_v, v.vertex));
}
}
}
return dis;
}
测试
测试案例(graph_testing.cpp):
#include "graph.hpp"
void test04(Graph<char> g) {
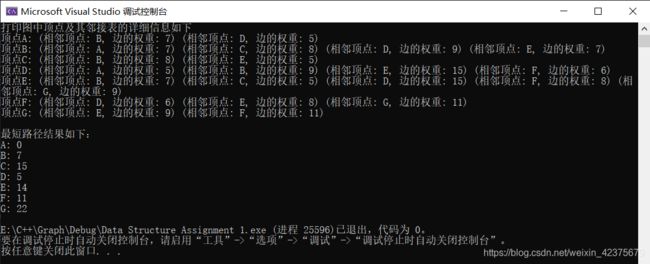
cout << "最短路径结果如下:" << endl;
auto dis = g.dijkstra('A');
vector<char> vertices = g.get_vertices();
for(auto vertex: vertices)
if (dis[vertex] >= 0)
cout << vertex<< ": " << dis[vertex] << endl;
}
int main()
{
Graph<char> g;
g.add_vertex('A');
g.add_vertex('B');
g.add_vertex('C');
g.add_vertex('D');
g.add_vertex('E');
g.add_vertex('F');
g.add_vertex('G');
g.add_edge('A', 'B', 7);
g.add_edge('A', 'D', 5);
g.add_edge('B', 'C', 8);
g.add_edge('B', 'D', 9);
g.add_edge('B', 'E', 7);
g.add_edge('C', 'E', 5);
g.add_edge('D', 'E', 15);
g.add_edge('D', 'F', 6);
g.add_edge('E', 'F', 8);
g.add_edge('E', 'G', 9);
g.add_edge('F', 'G', 11);
g.add_vertex('H');
g.add_edge('B', 'H', 9);
g.add_edge('A', 'H', 10);
g.add_edge('D', 'H', 11);
g.add_edge('A', 'H', 12);
g.remove_vertex('H');
cout << "打印图中顶点及其邻接表的详细信息如下" << endl;
g.show();
cout << endl;
test04(g);
return 0;
}