bigdecimal 保留两位小数_不要以为你用了BigDecimal后,计算结果就一定精确了
- bigdecimal
- 保留两位小数
- bigdecimal
- 保留小数
- bigdecimal
- 加减
- bigdecimal
- 加减乘除
- bigdecimal
- 四舍五入保留两位小数
- bigdecimal
- 科学计数转普通计数
异常再现
大家应该都已经知道,涉及到金钱的计算应该使用BigDecimal,没有使用BigDecimal的已经被开除。
但是使用了BigDecimal后计算结果就一定是精确的吗?未必。看下面测试
BigDecimal a = new BigDecimal(1.01); BigDecimal b = new BigDecimal(2.02); BigDecimal c = new BigDecimal("1.01"); BigDecimal d = new BigDecimal("2.02"); BigDecimal e = new BigDecimal(Double.toString(1.01)); BigDecimal f = new BigDecimal(Double.toString(2.02)); BigDecimal g = BigDecimal.valueOf(1.01); BigDecimal h = BigDecimal.valueOf(2.02); System.out.println(a.add(b)); System.out.println(c.add(d)); System.out.println(e.add(f)); System.out.println(g.add(h));输出结果为:
3.03000000000000002664535259100375697016716003417968753.033.033.03可以看到第一行输出是有问题的。
float和double精度问题
在java中,double是双精度,64位,浮点数,默认是0.0d。float是单精度,32位,浮点数,默认是0.0f;其中float的存储方式如下图所示:
而双精度的存储方式为:
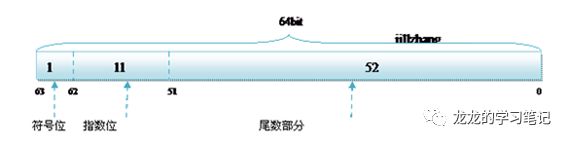 float和double的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的,其整数部分始终是一个隐含着的“1”,由于它是不变的,故不能对精度造成影响。
float和double的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的,其整数部分始终是一个隐含着的“1”,由于它是不变的,故不能对精度造成影响。
float:2^23 = 8388608,一共七位,这意味着最多能有7位有效数字,但绝对能保证的为6位,也即float的精度为6~7位有效数字;
double:2^52 = 4503599627370496,一共16位,同理,double的精度为15~16位。
为什么会精度丢失?
计算机在处理数据都涉及到数据的转换和各种复杂运算,比如,不同单位换算,不同进制(如二进制十进制)换算等,很多除法运算不能除尽,比如10÷3=3.3333.....无穷无尽,而精度是有限的,3.3333333x3并不等于10,经过复杂的处理后得到的十进制数据并不精确,精度越高越精确。float和double的精度是由尾数的位数来决定的,其整数部分始终是一个隐含着的“1”,由于它是不变的,故不能对精度造成影响。float:2^23 = 8388608,一共七位,由于最左为1的一位省略了,这意味着最多能表示8位数:28388608 = 16777216 。有8位有效数字,但绝对能保证的为7位,也即float的精度为78位有效数字;double:2^52 = 4503599627370496,一共16位,同理,double的精度为1617位。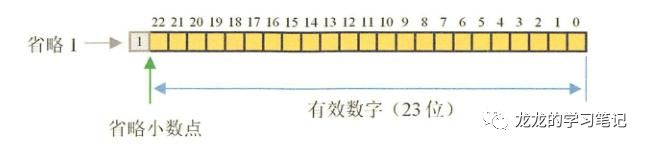
当到达一定值自动开始使用科学计数法,并保留相关精度的有效数字,所以结果是个近似数,并且指数为整数。在十进制中小数有些是无法完整用二进制表示的。所以只能用有限位来表示,从而在存储时可能就会有误差。对于十进制的小数转换成二进制采用乘2取整法进行计算,取掉整数部分后,剩下的小数继续乘以2,直到小数部分全为0。
BigDecimal分析
BigDecimal(double val)这个方法是无法保证精度的,源码注释中也已经写明:
/** * Translates a {@code double} into a {@code BigDecimal} which * is the exact decimal representation of the {@code double}'s * binary floating-point value. The scale of the returned * {@code BigDecimal} is the smallest value such that * (10scale × val) is an integer. * * Notes: * * * The results of this constructor can be somewhat unpredictable. * One might assume that writing {@code new BigDecimal(0.1)} in * Java creates a {@code BigDecimal} which is exactly equal to * 0.1 (an unscaled value of 1, with a scale of 1), but it is * actually equal to * 0.1000000000000000055511151231257827021181583404541015625. * This is because 0.1 cannot be represented exactly as a * {@code double} (or, for that matter, as a binary fraction of * any finite length). Thus, the value that is being passed * in to the constructor is not exactly equal to 0.1, * appearances notwithstanding. * * * The {@code String} constructor, on the other hand, is * perfectly predictable: writing {@code new BigDecimal("0.1")} * creates a {@code BigDecimal} which is exactly equal to * 0.1, as one would expect. Therefore, it is generally * recommended that the {@linkplain #BigDecimal(String) * String constructor} be used in preference to this one. * * * When a {@code double} must be used as a source for a * {@code BigDecimal}, note that this constructor provides an * exact conversion; it does not give the same result as * converting the {@code double} to a {@code String} using the * {@link Double#toString(double)} method and then using the * {@link #BigDecimal(String)} constructor. To get that result, * use the {@code static} {@link #valueOf(double)} method. * * * @param val {@code double} value to be converted to * {@code BigDecimal}. * @throws NumberFormatException if {@code val} is infinite or NaN. */ public BigDecimal(double val) { this(val,MathContext.UNLIMITED); }
并且告诉我们应该使用BigDecimal(String val):
public BigDecimal(String val) {
this(val.toCharArray(), 0, val.length()); }当然使用BigDecimal valueOf(double val)也是可以的,valueOf实际是先将double或flout的数据转为了string:
public static BigDecimal valueOf(double val) {
// Reminder: a zero double returns '0.0', so we cannot fastpath // to use the constant ZERO. This might be important enough to // justify a factory approach, a cache, or a few private // constants, later. return new BigDecimal(Double.toString(val)); }总结
(1)商业计算使用BigDecimal。
(2)使用参数类型为String的构造函数或valueOf()方法。
(3) BigDecimal都是不可变的(immutable)的,在进行每一步运算时,都会产生一个新的对象,所以在做加减乘除运算时千万要保存操作后的值。