基于信息增益的决策树特征选择算法（ID3算法）及python实现

基于信息增益的决策树算法（ID3算法）及python实现

决策树概述

不同于逻辑回归，决策树属于非线性模型，可以用于分类，也可用于回归。它是一种树形结构，可以认为是if-then规则的集合，是以实例为基础的归纳学习。基本思想是自顶向下，以信息增益（或信息增益比，基尼系数等）为度量构建一颗度量标准下降最快的树，每个内部节点代表一个属性的测试，直到叶子节点处只剩下同一类别的样本。它的决策流程如下所示：

决策树的学习包括三个重要的步骤，特征选择，决策树的生成以及决策树的剪枝。

• 特征选择：常用的特征选择有信息增益，信息增益比，基尼系数等。
• 生成过程：通过计算信息增益或其它指标，选择最佳特征。从根结点开始，递归地产生决策树，不断的选取局部最优的特征，将训练集分割成能够基本正确分类的子集。
• 剪枝过程：首先定义决策树的评价指标，对于所有的叶子结点，累加计算每个叶子结点中的（样本数）与其（叶子节点熵值）的乘积，以叶子数目作为正则项（它的系数为剪枝系数）。然后计算每个结点的剪枝系数，它的大概含义是删除该结点的子树，损失不变的前提下，正则项系数的值为多少，这个值越小说明该子树越没有存在的必要。依次选取剪枝系数最小的结点剪枝，得到决策树序列，通过交叉验证得到最优子树。

信息增益 (Information Gain)理论

提到信息增益必须先解释一下什么是“信息熵”，因为信息增益是基于信息熵而定义的。我们先给出信息熵的公式定义：

D：表示当前的数据集合。
k：表示当前数据集合中的第k类，也就是我们目标变量的类型。
最后，解释一下信息熵公式的由来：

信息论之父克劳德香农总结出信息熵的三条性质：

• 单调性，发生概率越高的事件，其所携带的信息熵越低。极端案例即是“太阳从东方升起”，因为是确定事件，所以不携带任何信息量。从信息论的角度，认为这句话没有消除任何不确定性。
• 非负性：信息熵不能为负，因为负的信息，在得知某个信息后，却增加了不确定性是不合理的。
• 累加性：多个随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和，即：
  事件X=A,Y=B同时发生，两个时间相互独立，
  
  则信息熵为：
  

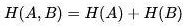
香浓从数学上，严格证明了满足上述三个条件的随机变量不确定性度量函数具有唯一形式：

其中的C为常数，将其归一化为C=1，即得到信息熵公式。
补充一下：如果两个事件不相互独立，则满足：
H（A,B）=H(A)+H(B)-I(A,B)，其中I(A,B)是互信息，代表一个随机变量包含另一个随机变量信息量的度量。
信息熵的取值范围为0到1，值越大，越不纯，值越小，集合纯度越高。如下图所示：

上面信息熵只能代表不纯度，并不能代表信息量。但既然我们有了不纯度，我们只要将分类前后的不纯度相减，那就可以得到一种 “纯度提升值” 的指标，我们把它叫做 “信息增益”，公式如下：

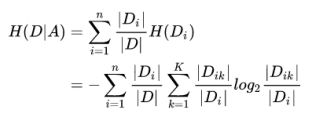
基于信息增益的决策树特征选择方法

• 基于特征A对数据集D的划分：
  H(D|A)：表示基于特征A（分类后）的信息熵，也称条件熵。
  Di：基于特征A对数据集D划分的子集。
  |Di|/|D|：考虑到特征分类子集的数据量不同，给每个子集赋予了权重。
  n：为特征A的分类总数，即有多少个Di。
• 基于目标分类对特征类别Di数据集的划分：
  Dik：每个特征分类子集Di中目标分类后的子集。
  K：为目标分类的类别总数，即有多少个Dik。
  |Dik|/|Di|：每个特征分类子集中，各目标分类子子集所占比例。

简单来说，先基于特征A进行划分，再基于目标变量进行划分，这是一个嵌套的过程。举一个例子说明，红色框内代表决策树中的其中一个分类过程，按照“是否理解内容”这个特征分成两类，树的父集和子集信息熵都已经标出，因此信息增益Gain就可以计算出来。

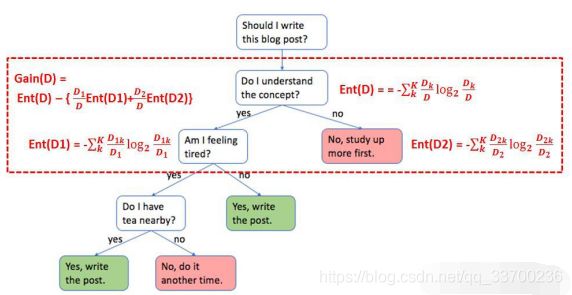
上面只是描述了针对一个特征的计算信息增益的过程。在实际决策过程中，我们需要将所有的特征分类后的信息增益都计算一遍，然后选择其中最大的一个最为本次的分类特征。因此也就达到了特征选择的目的。ID3算法使用信息增益的方法来选择特征。
从这个过程，我们可以发现：最开始选择的特征肯定是提供信息量最大的，因为它是遍历所有特征后选择的结果。因此，按照决策过程中特征从上到下的顺序，我们也可以将特征的重要程度进行排序。这也就解释了为什么树模型有feature_importance这个参数了。

算法的python实现

# -*- coding: utf-8 -*-
"""
Created on Sat Mar 30 11:17:53 2019

@author: Auser
"""
from math import log
import operator


def cal_entropy(dataSet_train):#计算熵
 
    #numEntries为训练集样本数
    numEntries = len(dataSet_train)
    labelCounts = {
     }
    for featVec in dataSet_train:#遍历训练样本
        label = featVec[-1]#将每个训练样本的类别标签作为类别列表
        if label not in labelCounts.keys():#如果一个训练样本的类别不在类别列表字典中
            labelCounts[label] = 0#将该训练样本类别进行标记
        labelCounts[label] += 1#否则，给类别字典对应的类别+1
    entropy = 0.0#初始化香浓商
    for key in labelCounts.keys():#遍历类别字典的每个类别
        p_i = float(labelCounts[key]/numEntries)#计算每个类别的样本数占总的训练样本数的占比（即某一样本是类i的概率）
        entropy -= p_i * log(p_i,2)#log(x,10)表示以10 为底的对数，计算香浓熵
    return entropy

 
def split_data(dataSet_train,feature_index,value):#按照选出的最优的特征的特征值将训练集进行分裂，并将使用过的特征进行删除
    '''
    划分数据集
    feature_index：用于划分特征的列数，例如“年龄”
    value:划分后的属性值：例如“青少年”
    '''
    data_split=[]#划分后的数据集
    for feature in dataSet_train:#遍历训练集
        if feature[feature_index]==value:#如果训练集的特征索引的值等于划分后的属性值
            reFeature=feature[:feature_index]#删除使用过的特征
            reFeature=list(reFeature)
            reFeature.extend(feature[feature_index+1:])
            data_split.append(reFeature)
    return data_split

def choose_best_to_split(dataSet_train):#
    
    '''
    根据每个特征的信息增益率，选择最大的划分数据集的索引特征
    '''
    
    count_feature=len(dataSet_train[0])-1#特征个数4
    #print(count_feature)#4
    entropy=cal_entropy(dataSet_train)#原数据初始的信息熵
    #print(entropy)#0.9402859586706309
    
    max_info_gain=0.0#信息增益率最大
    split_fea_index=-1#信息增益率最大，对应的特征索引号
    #split_fea_value=0#信息增益率最大没对应的特征的特征值
 
    for i in range(count_feature):#遍历特征
        
        feature_list=[fe_index[i] for fe_index in dataSet_train]#分别获取每每个元组的第i个特征值
        #######################################
 
       # print(feature_list)
        unqval=set(feature_list)#去除每一个特征重复的特征值
        Pro_entropy=0.0#初始化条件熵
        for value in unqval:#遍历该特征下的所有属性的唯一值
            sub_data=split_data(dataSet_train,i,value)#将分裂后的数据作为子数据集，递归使用某一特征i的每个特征值来分裂训练集
            pro=len(sub_data)/float(len(dataSet_train))#某一训练样本是某一子集的概率，分裂后每一个子集占训练集总数的概率
            Pro_entropy+=pro*cal_entropy(sub_data)#在某一属性i下的条件熵
            #print(Pro_entropy)
            
        info_gain=entropy-Pro_entropy#一个训练样本在某一属性下的信息增益
       # print('第%d个特征的增益为%.3f'%(i,info_gain))
        if(info_gain>max_info_gain):#选择值最大的信息增益
            max_info_gain=info_gain
            split_fea_index=i
           # split_fea_value=value

    return split_fea_index#返回分裂特征值对应的特征索引
        
        
##################################################
def most_occur_label(classList):
    #sorted_label_count[0][0]  次数最多的类标签
    label_count={
     }#创建类别标签字典，key为类别，item为每个类别的样本数
    for label in classList:#遍历类列表
        if label not in label_count.keys():#如果类标签不在类别标签的字典中
            label_count[label]=0#将该类别标签置为零
        else:
            label_count[label]+=1#否则，给对应的类别标签+1
            #按照类别字典的值排序
    sorted_label_count = sorted(label_count.items(),key = operator.itemgetter(1),reverse = True)
    return sorted_label_count[0][0]#返回样本量最多的类别标签



def build_decesion_tree(dataSet_train,featnames):#建立决策树
    '''
    字典的键存放节点信息，分支及叶子节点存放值
    '''
    featname = featnames[:]              ################特证名
    classlist = [featvec[-1] for featvec in dataSet_train]  #此节点的分类情况
    if classlist.count(classlist[0]) == len(classlist):  #全部属于一类
        return classlist[0]
    if len(dataSet_train[0]) == 1:         #分完了,没有属性了
        return  most_occur_label(classlist)       #少数服从多数，返回训练样本数最多的类别作为叶节点
    # 选择一个最优特征的最优特征值进行划分
    bestFeat = choose_best_to_split(dataSet_train)
    bestFeatname = featname[bestFeat]
    del(featname[bestFeat])     #防止下标不准
    DecisionTree = {
     bestFeatname:{
     }}
    #print(DecisionTree)
    # 创建分支,先找出所有属性值,即分支数
    allvalue = [vec[bestFeat] for vec in dataSet_train]#将每个训练样本的最优特征值作为分裂时的特征值
    specvalue = sorted(list(set(allvalue)))  #对分支使有一定顺序
    for v in specvalue:#遍历选中的最优特征的每个特征取值
        copyfeatname = featname[:]#复制特证名，在下一轮建造子树时使用
        #print(copyfeatname)
        #递归建造决策树，split——data()对源数据集进行分裂，
        DecisionTree[bestFeatname][v] =  build_decesion_tree(split_data(dataSet_train,bestFeat,v),copyfeatname)
    return DecisionTree


 
def classify(Tree, featnames, X):#对测试集使用训练好的决策树进行分类
    #classLabel=' '
    global classLabel
    root = list(Tree.keys())[0]#构建树的根
    #print(root)
    firstDict = Tree[root]#树的根给第一个字典
    #print(firstDict)
    featindex = featnames.index(root)  #根节点的属性下标
    #print(featindex)
    #classLabel='0'
    for key in firstDict.keys():   #遍历每一个子树的关键字的特征值
        if X[featindex] == key:#如果测试样本指定特征索引的特征值等于关键字对应特征的特征值
            if type(firstDict[key]) == type({
     }):#当一个子树的关键字特征是字典，则说明该子树还有下一级
                #print(type(firstDict[key]))
                #print(type({}))
                classLabel = classify(firstDict[key],featnames,X)#使用递归对下一级进行分类
            else:#否则如果当一个子树的关键字特征不是字典则将该值赋给类别
                classLabel = firstDict[key]
    return classLabel#返回求得的类别


#计算叶结点数
def getNumLeafs(Tree):
    numLeafs = 0
    firstStr = list(Tree.keys())[0]
    secondDict = Tree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':# 测试结点的数据类型是否为字典
            numLeafs += getNumLeafs(secondDict[key])
        else:   numLeafs +=1
    return numLeafs


# 计算树的深度
def getTreeDepth(Tree):
    maxDepth = 0
    firstStr = list(Tree.keys())[0]
    secondDict = Tree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':# 测试结点的数据类型是否为字典
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:   thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth