logistic回归_R语言实现logistic回归
引言:前面我们已经掌握了logistic回归的知识点,今天就来看看如何用R语言实现logistic回归。今天用到的数据来源于机器学习仓库,基于患者的一些信息以判定该患者是否患有心脏病(heart disease, hd),链接如下:http://archive.ics.uci.edu/ml/datasets/Heart+Disease
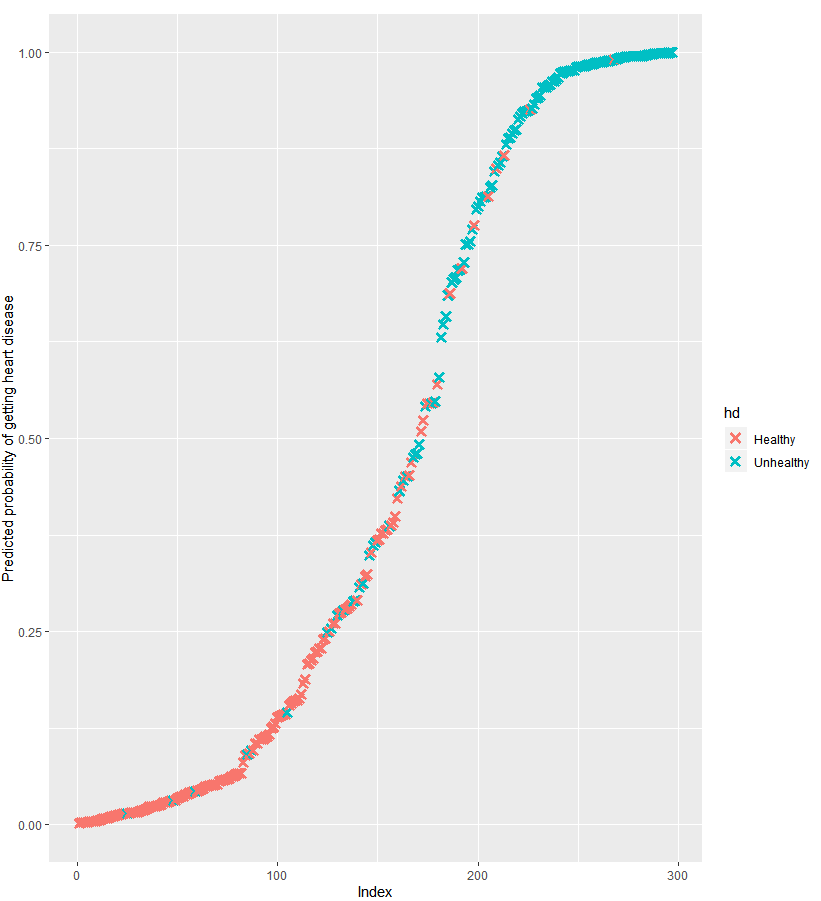 基于较复杂的模型,得出一个连续型的模型。总体而言,该模型能够将绝大部分的患者判定为患者,其对应的患病的p值>0.5;绝大部分的非患者被判定为非患者,其对应患病的p值<0.5。 参考视频:https://www.youtube.com/watch?v=C4N3_XJJ-jU
基于较复杂的模型,得出一个连续型的模型。总体而言,该模型能够将绝大部分的患者判定为患者,其对应的患病的p值>0.5;绝大部分的非患者被判定为非患者,其对应患病的p值<0.5。 参考视频:https://www.youtube.com/watch?v=C4N3_XJJ-jU
1. 数据读取
### 1 读取UCI机器学习中的数据
url "http://archive.ics.uci.edu/ml/machine-learning-databases/heart-disease/processed.cleveland.data"
data FALSE)
# 查看数据
head(data) # 该数据不含有列名,我们很难知道每列代表的意义
# V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14
# 1 63 1 1 145 233 1 2 150 0 2.3 3 0.0 6.0 0
# 2 67 1 4 160 286 0 2 108 1 1.5 2 3.0 3.0 2
# 3 67 1 4 120 229 0 2 129 1 2.6 2 2.0 7.0 1
# 4 37 1 3 130 250 0 0 187 0 3.5 3 0.0 3.0 0
# 5 41 0 2 130 204 0 2 172 0 1.4 1 0.0 3.0 0
# 6 56 1 2 120 236 0 0 178 0 0.8 1 0.0 3.0 0
# 根据机器学习仓库中的数据注释添加列名,便于解读数据的意义
colnames(data) "age",
"sex",# 0 = female, 1 = male
"cp", # chest pain
# 1 = typical angina,
# 2 = atypical angina,
# 3 = non-anginal pain,
# 4 = asymptomatic
"trestbps", # resting blood pressure (in mm Hg)
"chol", # serum cholestoral in mg/dl
"fbs", # fasting blood sugar if less than 120 mg/dl, 1 = TRUE, 0 = FALSE
"restecg", # resting electrocardiographic results
# 1 = normal
# 2 = having ST-T wave abnormality
# 3 = showing probable or definite left ventricular hypertrophy
"thalach", # maximum heart rate achieved
"exang", # exercise induced angina, 1 = yes, 0 = no
"oldpeak", # ST depression induced by exercise relative to rest
"slope", # the slope of the peak exercise ST segment
# 1 = upsloping
# 2 = flat
# 3 = downsloping
"ca", # number of major vessels (0-3) colored by fluoroscopy
"thal", # this is short of thalium heart scan
# 3 = normal (no cold spots)
# 6 = fixed defect (cold spots during rest and exercise)
# 7 = reversible defect (when cold spots only appear during exercise)
"hd" # (the predicted attribute) - diagnosis of heart disease 心脏病的诊断属性
# 0 if less than or equal to 50% diameter narrowing
# 1 if greater than 50% diameter narrowing
)
### 查看增加列名后的数据
head(data)
# age sex cp trestbps chol fbs restecg thalach exang oldpeak slope ca thal hd
# 1 63 1 1 145 233 1 2 150 0 2.3 3 0.0 6.0 0
# 2 67 1 4 160 286 0 2 108 1 1.5 2 3.0 3.0 2
# 3 67 1 4 120 229 0 2 129 1 2.6 2 2.0 7.0 1
### 查看数据的整体情况
# 'data.frame': 303 obs. of 14 variables:
# $ age : num 63 67 67 37 41 56 62 57 63 53 ... #年龄数值变量
# $ sex : num 1 1 1 1 0 1 0 0 1 1 ... #性别,数值型变量(应改为因子型变量)
# $ cp : num 1 4 4 3 2 2 4 4 4 4 ... #胸痛情况(应改为因子型变量)
# $ trestbps: num 145 160 120 130 130 120 140 120 130 140 ...
# $ chol : num 233 286 229 250 204 236 268 354 254 203 ...
# $ fbs : num 1 0 0 0 0 0 0 0 0 1 ... #空腹血糖是否满足小于120 mg/dl(应改为因子型变量)
# ......
# ......
2. 数据预处理(确保数据能够在程序中被正常识别)
数据类型的整理:将分类变量设置为factor,连续型变量为num保持不变,删除缺失值记录。
### 2 数据预处理
# str(data) 查看数据的整体情况,判断哪些变量需要进行类型转换
## "?"为字符型数据,将"?"转换为NA
data[data == "?"] NA
## 将分类变量设置为factor,连续型变量为num保持不变
# 这一步是确保数据能够在程序中被正确识别
data[data$sex == 0,]$sex "F"
data[data$sex == 1,]$sex "M"
data$sex
data$cp data$fbs data$restecg data$exang data$slope
data$ca #R将"?"认为是字符型,故需要修正为整数型
data$ca #将整数型改为因子型
data$thal # "thal"中也有"?",处理同ca
data$thal
## 将hd(heart disease)中的数字(0~4)改成"Healthy" 和"Unhealthy"
data$hd 0, yes="Healthy", no="Unhealthy")
data$hd str(data) #再次核验数据类型再次查看转换后的数据类型:所有的分类变量被转换成因子型(factor),所有的连续变量保持数值型(num)。
NA值的处理:如果NA较少,可以直接删除;如果NA较多,应该使用随机森林或其他方法替代NA。
## 查看NA个数
table(is.na(data))
# FALSE TRUE
# 4236 6
##展示含有NA的记录
data[!complete.cases(data),]
# age sex cp trestbps chol fbs restecg thalach exang oldpeak slope ca thal hd
# 88 53 F 3 128 216 0 2 115 0 0.0 1 2 Healthy
# 167 52 M 3 138 223 0 0 169 0 0.0 1 2 Healthy
# 193 43 M 4 132 247 1 2 143 1 0.1 2 4 Unhealthy
# 267 52 M 4 128 204 1 0 156 1 1.0 2 2 Unhealthy
# 288 58 M 2 125 220 0 0 144 0 0.4 2 4 Healthy
# 303 38 M 3 138 175 0 0 173 0 0.0 1 2 Healthy
##去除含NA的样本(6个样本),仅保留完整数据的样本(297个样本)
data nrow(data)
# [1] 2973. 数据质量控制
### 3 数据质量控制
# 确保因子型数据中的每一个类别都有患者和非患者
# 删除仅含有1-2个样本的类别。因为其对odds或log(odds)有较大的效应量
xtabs(~ hd + sex, data=data)
xtabs(~ hd + cp, data=data)
xtabs(~ hd + fbs, data=data)
xtabs(~ hd + exang, data=data)
xtabs(~ hd + slope, data=data)
xtabs(~ hd + ca, data=data)
xtabs(~ hd + thal, data=data)
xtabs(~ hd + restecg, data=data) ##restecg事件的类别1仅含有4个样本。暂时保留,观察其对结局判定的影响
# restecg
#hd 0 1 2
# Healthy 92 1 67
# Unhealthy 55 3 79
4. 简单logistic回归(基于单一变量性别预测是否患有心脏病)
# 4 简单logistic回归:基于单一变量(性别)预测患者是否患有心脏病(hd)
## 4.1 查看原始数据
xtabs(~ hd + sex, data=data)
# sex
# hd F M
# Healthy 71 89
# Unhealthy 25 112
## 大多数男性是患者,而大多数女性不是患者
## 男性是患者的优势比更大(112/89);女性是患者的优势比较小(25/71)
## 换句话说,男性增加心脏病发生的优势,男性更容易发生心脏病glm()执行logistic回归:
## 4.2 进行logistic回归
## glm()是执行广义线性模型(generalized linear models)的函数,
## “hd~sex”表示基于性别预测hd
## 指定binomial family产生广义线性模型,使glm()执行logistic回归而不是其他类型的广义线性模型
## glm()函数一步搞定logistic回归
logistic "binomial")
summary(logistic)查看logistic回归结果:
##查看logistic回归结果
summary(logistic)
# Call:# glm(formula = hd ~ sex, family = "binomial", data = data)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -1.2765 -1.2765 -0.7768 1.0815 1.6404
#
# Coefficients:# Estimate Std. Error z value Pr(>|z|) # (Intercept) -1.0438 0.2326 -4.488 7.18e-06 ***# sexM 1.2737 0.2725 4.674 2.95e-06 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# (Dispersion parameter for binomial family taken to be 1)
#
# Null deviance: 409.95 on 296 degrees of freedom
# Residual deviance: 386.12 on 295 degrees of freedom
# AIC: 390.12
#
# Number of Fisher Scoring iterations: 4
logistic回归结果解读:
第一个系数:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.0438 0.2326 -4.488 7.18e-06 ***
- 截距系数指的是女性患者发生心脏病的优势比的对数,即log(OR)。
- 因子水平:因为在设置因子时,R默认按照字母表顺序进行排序:female(0),male(1)。故female为基线水平,即截距水平。
- 该截距的计算结果与下面的结果相同:
- female.log.odds
第二个系数:
Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.0438 0.2326 -4.488 7.18e-06 ***
## sexM 1.2737 0.2725 4.674 2.95e-06 ***
结合两个系数,可得出对应的logistic回归曲线方程:
heart disease = -1.0438 + 1.2737 x the patient is male
如果该患者是女性:the patient is male对应数字0。
heart disease = -1.0438 + 1.2737 x 0
如果该患者是男性:the patient is male对应数字1。
heart disease = -1.0438 + 1.2737 x 1
- SexM系数表示如果该样本为男性,其发生心脏病的优势比的对数(log(OR))比女性增加1.27倍。
- SexM系数的计算结果与下面的结果相同:male.log.odds.ratio
- Std.Error和z value是基于Wald检验计算得出,最后一列是相应的p值。这里的p值均小于0.05,故认为logistic回归的系数是具有显著性的。
系数的指数化,增加系数的可读性
exp(logistic$coefficients[1])
# 0.3521127
# 表明女性发生心脏病的优势比为0.35
exp(logistic$coefficients[2])
# 3.573933
# 表明男性发生心脏病的优势比女性增加3.57倍计算伪R2和p值
## 参考: 饱和模型与偏差计算R方与p值## logistic回归中:查看logistic回归的预测结果(基于性别预测是否患病的结果)
predicted.data probability.of.hd=logistic$fitted.values,
sex=data$sex)
str(predicted.data)
# 'data.frame': 297 obs. of 2 variables:
# $ probability.of.hd: num 0.557 0.557 0.557 0.557 0.26 ...
# $ sex : Factor w/ 2 levels "F","M": 2 2 2 2 1 2 1 1 2 2 ...利用ggplot2 R 包将预测结果可视化:
library("ggplot2")
ggplot(data=predicted.data, aes(x=sex, y=probability.of.hd)) +
geom_point(aes(color=sex), size=5) +
xlab("Sex") +
ylab("Predicted probability of getting heart disease")
## 在预测结果中,仅有两个概率值(男性一个,女性一个)
## 故可使用交叉表进行汇总预测结果
xtabs(~ probability.of.hd + sex, data=predicted.data)
# sex
# probability.of.hd F M
# 0.260416666667241 96 0
# 0.55721393034826 0 201
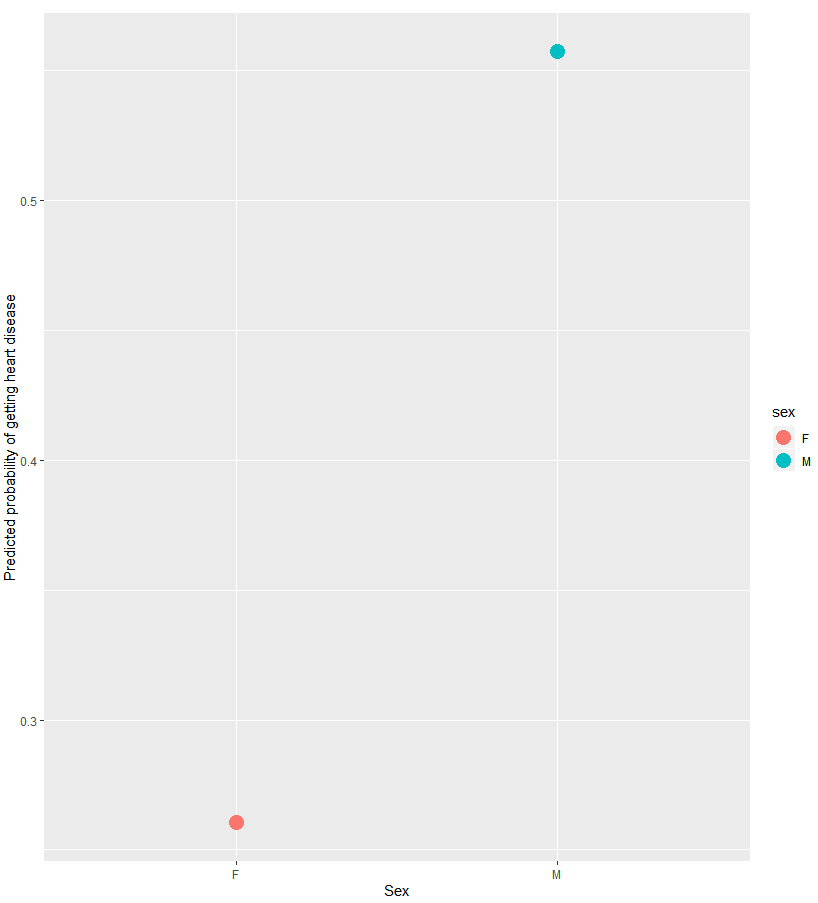 基于该模型,我们仅能根据性别判断出两个概率,女性发病的概率较低(p=0.26),而男性发病的概率较高(p=0.56)。
基于该模型,我们仅能根据性别判断出两个概率,女性发病的概率较低(p=0.26),而男性发病的概率较高(p=0.56)。
5. 较多变量的logistic回归
##"hd~."表示使用数据中所有变量
logistic "binomial")
summary(logistic)
# Call:
# glm(formula = hd ~ ., family = "binomial", data = data)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -3.0490 -0.4847 -0.1213 0.3039 2.9086
#
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -6.253978 2.960399 -2.113 0.034640 *
# age -0.023508 0.025122 -0.936 0.349402
# sexM 1.670152 0.552486 3.023 0.002503 **
# cp2 1.448396 0.809136 1.790 0.073446 .
# cp3 0.393353 0.700338 0.562 0.574347
# cp4 2.373287 0.709094 3.347 0.000817 ***
# trestbps 0.027720 0.011748 2.359 0.018300 *
# chol 0.004445 0.004091 1.087 0.277253
# fbs1 -0.574079 0.592539 -0.969 0.332622
# restecg1 1.000887 2.638393 0.379 0.704424
# restecg2 0.486408 0.396327 1.227 0.219713
# thalach -0.019695 0.011717 -1.681 0.092781 .
# exang1 0.653306 0.447445 1.460 0.144267
# oldpeak 0.390679 0.239173 1.633 0.102373
# slope2 1.302289 0.486197 2.679 0.007395 **
# slope3 0.606760 0.939324 0.646 0.518309
# ca3 2.237444 0.514770 4.346 1.38e-05 ***
# ca4 3.271852 0.785123 4.167 3.08e-05 ***
# ca5 2.188715 0.928644 2.357 0.018428 *
# thal3 -0.168439 0.810310 -0.208 0.835331
# thal4 1.433319 0.440567 3.253 0.001141 **
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# (Dispersion parameter for binomial family taken to be 1)
#
# Null deviance: 409.95 on 296 degrees of freedom
# Residual deviance: 183.10 on 276 degrees of freedom
# AIC: 225.1
#
# Number of Fisher Scoring iterations: 6
输出的结果较多,但是解释的方法同前。一些变量的系数具有显著性,一些变量的系数不具有显著性。
## 计算该模型的 "Pseudo R-squared"和 p-value
ll.null 2
ll.proposed 2## McFadden's Pseudo R^2 = [ LL(Null) - LL(Proposed) ] / LL(Null)
(ll.null - ll.proposed) / ll.null# [1] 0.5533531##R^2的P值1 - pchisq(2*(ll.proposed - ll.null), df=(length(logistic$coefficients)-1))# [1] 0# p值非常小,趋近0## 可视化该模型的预测结果
predicted.data
probability.of.hd=logistic$fitted.values,
hd=data$hd)
str(predicted.data)# 'data.frame': 297 obs. of 2 variables:# $ probability.of.hd: num 0.0621 0.9934 0.9979 0.1136 0.0263 ...# $ hd : Factor w/ 2 levels "Healthy","Unhealthy": 1 2 2 1 1 1 2 1 2 2 ..## 对预测结果进行排序:按照预测发生心脏病的概率大小predicted.data
order(predicted.data$probability.of.hd, decreasing=FALSE),]
predicted.data$rank 1:nrow(predicted.data)## 可视化预测结果:不同的颜色展示患病或不患病的真实分类ggplot(data=predicted.data, aes(x=rank, y=probability.of.hd)) +
geom_point(aes(color=hd), alpha=1, shape=4, stroke=2) +
xlab("Index") +
ylab("Predicted probability of getting heart disease")
ggsave("heart_disease_probabilities.pdf") 基于较复杂的模型,得出一个连续型的模型。总体而言,该模型能够将绝大部分的患者判定为患者,其对应的患病的p值>0.5;绝大部分的非患者被判定为非患者,其对应患病的p值<0.5。 参考视频:https://www.youtube.com/watch?v=C4N3_XJJ-jU
基于较复杂的模型,得出一个连续型的模型。总体而言,该模型能够将绝大部分的患者判定为患者,其对应的患病的p值>0.5;绝大部分的非患者被判定为非患者,其对应患病的p值<0.5。 参考视频:https://www.youtube.com/watch?v=C4N3_XJJ-jU
编辑:吕琼
校审:罗鹏
