MATLAB新手简明使用教程（十一）——三维中的数据可视化，使用matlab绘图——新手来看，保证看懂

今日目标

上一讲介绍了二维的画图以及一个函数 plot() 的详细介绍，今天看matlab中三维绘图。

今天我们会学会如何在matlab中绘制简单的三维图像，以及理解一些常用函数。

开始啦

三维中有plot()吗？

在三维画图中，有对应的 plot3() 函数用于画三维空间中的图像，但是，我们回忆一下plot是如何工作的：

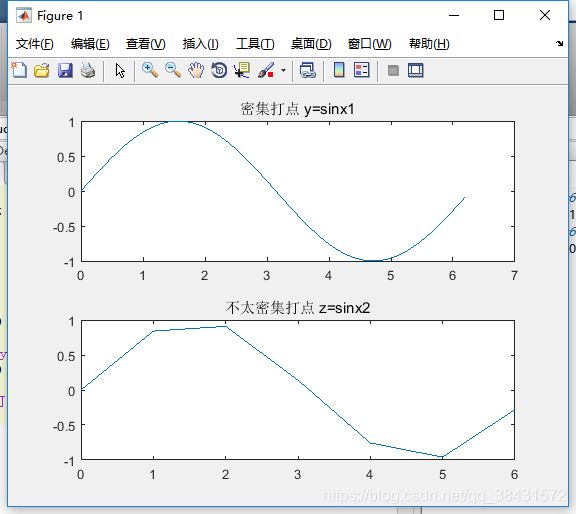
plot接收的参数是矩阵（或者说数组），然后根据传入的参数画点，使用直线把点连接起来，如果点足够密集，展示出来后，在我们眼睛看来，画出来就是一个曲线。

下面我们看一个对比图：

代码如下： 

%% plot对比
x1 = 0:0.1:2*pi;    % x1 每两个点的距离是0.1
y = sin(x1);
x2 = 0:1:2*pi;      % x2 每两个点的距离是1
z = sin(x2);
figure;
subplot(2, 1, 1);   % 分块画图
plot(x1, y);        % 画sinx1
title('密集打点 y=sinx1')
subplot(2, 1, 2);
plot(x2, z);        % 画sinx2
title('不太密集打点 z=sinx2');

 而 plot3() 同样，也是在传入的三个矩阵中找三维空间中的点，然后使用直线连接，所以可以很直观的理解到：plot3() 是画的空间曲线（直线）。我们下面看个例子：

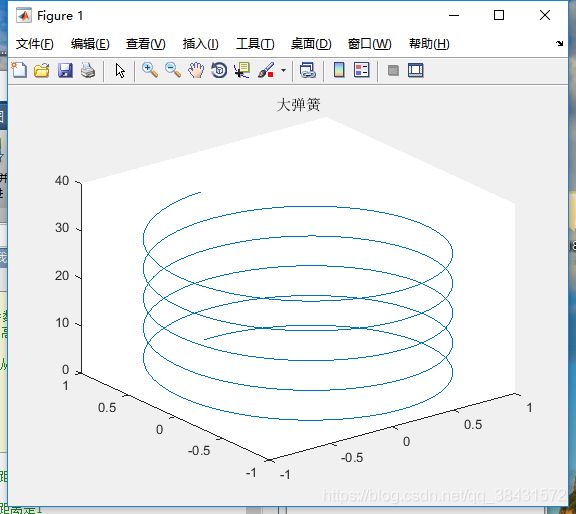
%% 使用plot3 画一个螺旋向上的线
t = 0:0.1:10*pi;    % 空间曲线使用参数方程比较容易表示出来
z = t;          % z轴随着t的增加而升高
x = sin(t);
y = cos(t);     % x^2+y^2 = 1，所以从上向下看是空间圆
figure;
plot3(x, y, z); % 画图
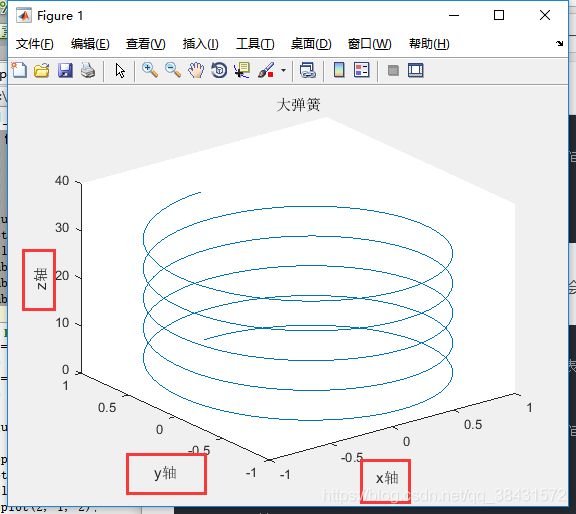
title('大弹簧');

其余的参数和二维中的plot 大同小异，相信大家都能会了，这里还有一个小知识点，补充一下：如果我们想给坐标轴命名，使用下面的代码：

%% 使用plot3 画一个螺旋向上的线
t = 0:0.1:10*pi;    % 空间曲线使用参数方程比较容易表示出来
z = t;          % z轴随着t的增加而升高
x = sin(t);
y = cos(t);     % x^2+y^2 = 1，所以从上向下看是空间圆
figure;
plot3(x, y, z); % 画图
title('大弹簧');
xlabel('x轴')
ylabel('y轴')
zlabel('z轴')

在二维中，不写zlabel即可，如图：

我想画曲面，怎么画？

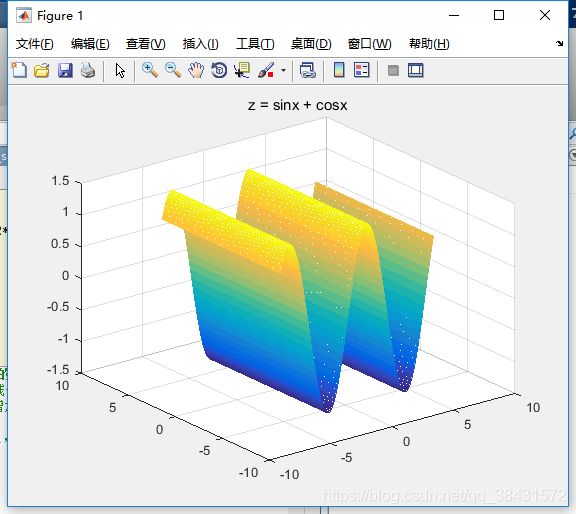
在第八讲中我们稍微提了一下meshgrid()和mesh()画出一个空间曲面，我们先来回顾一下这两个函数（假设我们画z = sinx + cosx吧，随便捏造的函数）：

代码如下：

%% meshgrid和mesh的使用
clear all;
[x, y] = meshgrid(-2*pi:0.1:2*pi, -2*pi:0.1:2*pi);
z = sin(x) + cos(x);
figure;
mesh(x, y, z);
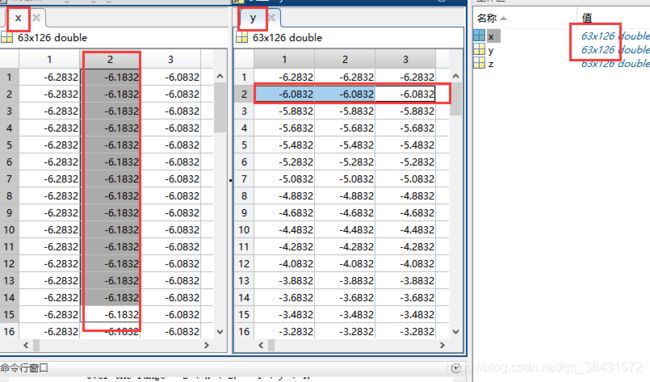
title('z = sinx + cosx');

[x, y] = meshgrid(a, b) 参数到底如何工作呢？我们看看这个结果的工作区：

我们发现，x和y是两个126行和126列的数组（严格来讲，应该叫126阶方阵），并且仔细观察，x的列和y的行一样，也就是说，x和y在这个meshgrid(-2*pi:0.1:2*pi, -2*pi:0.1:2*pi)下存在转置关系，那这个转置关系换了变量区间还存在吗？动手实验一下：

[x, y] = meshgrid(-2*pi:0.1:2*pi, -2*pi:0.2:2*pi);  % 这句话改为这个，第二个的分区更粗糙了一点

然后我们发现转置关系不存在了，甚至x和y都不是方阵了，结果的x和y如下（注意）：

可以看到，x和y都是63行和126列，而我们的区间是：

-2*pi:0.1:2*pi, -2*pi:0.2:2*pi

也就是说，前面的那一个分出了126个区间点（记为a），后面那一个分出了63个区间点（记为b），所以结果得到的两个矩阵都是 b 行 a 列的！ 小心，不要记反了，是 b 行 a 列。上面这个来讲，结果是63行，126列。

接下来我们看里面的值，x 中，每一列都是相同的元素，总共63行，126列，共126个不同元素。y 中，每一行都是相同的元素，总共63行，126列， 共63个不同元素。

而 a 中有126个区间点， b 中共有63个区间点，所以，很轻易得出 [x, y]meshgrid(a, b)  的工作模式如下

meshgrid接受两个参数，a 和 b ，每个参数（a 或者 b）都是一个一维数组（严格来讲，叫做向量），假设 a 中有126个元素（即126个区间点，记为na），b 中有63个元素（即63个区间点记为nb），那么，结果x 和 y 均是 nb 行 na  列的矩阵（二维数组），并且对于 x ，每一行均为 a 的复制，共nb行（即 x 中有63行 a），而对于 y，每一列均为 b （的转置）的复制，共na列（即 y 中有126列 b）。

为了证明这个结论，我们可以假设 a = [1, 2, 3]，b = [4, 5]，按照上面的结论，得出的 x 和 y应该分别是：

x = [1 2 3,                     y = [4 4 4,

       1 2 3 ]                           5 5 5]

即: a = [1, 2, 3], na = 3; b = [4, 5], nb = 2，所以 x 是 nb 行 a，y 是 na 列 b（的转置）；现在跑代码验证结论：

可见，我们的猜想是对的！！

meshgrid()参数形式

如果只传递一个参数，如[x, y] = meshgrid(a)，那么这个语句等同于 [x, y] = meshgrid(a, a)；

如果得到三维的：[x, y, z] = meshgrid(a, b, c)；这时，输出的尺寸是 na行 nb 列，总共 nc 层。大家可以测试分析这个的数据怎么分配的，很简单，就当作小任务了，可以用这套数据：

%% 深入理解 meshgrid。
clear all;
[x, y, z] = meshgrid([1 2 3 4], [3 4 5], [5 6]);

结果如下：

如果上面的大家理解了，相信这个大家几乎能直接看出来规律了，那么这个知识点就过去啦！！

surf 画曲面

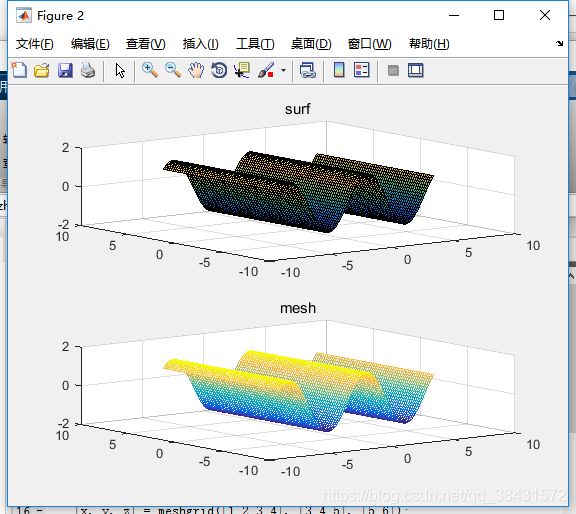
其实，mesh() 画出来的图形是一个个的方格，真正画曲面，还是要用其他的，比如 surf() ，使用方法和 mesh 几乎一模一样，我直接上代码和结果了：

%% meshgrid和surf的使用
clear all;
[x, y] = meshgrid(-2*pi:0.1:2*pi, -2*pi:0.2:2*pi);
z = sin(x) + cos(x);
figure;
subplot(2, 1, 1);
surf(x, y, z);      % surf画曲面
title('surf');
subplot(2, 1, 2);
mesh(x, y, z);      % mesh画方格
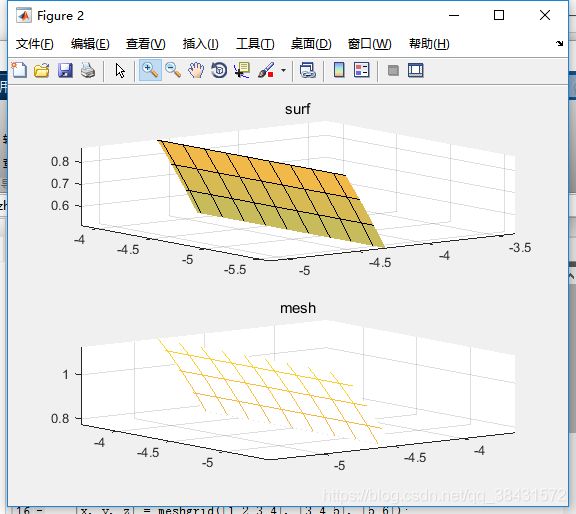
title('mesh');

其实这看不出来什么不同，我们可以使用这个工具放大：

现在，差距就非常明显了（其实这个无所谓的）

结束语

今天学习了如何再matlab中绘制三维的曲面和曲线，知识量看起来有点大，但是想一想，其实只有几个函数而已，加油！！！

如果觉得学习到了的话，点个赞吧。谢谢啦。