机器学习 聚类篇——DBSCAN的参数选择及其应用于离群值检测

摘要

DBSCAN（Density-Based Spatial Clustering of Applications with Noise） 为一种基于密度的聚类算法，本文主要介绍了DBSCAN算法的原理和参数选择方法，并实现了一个离群值检测案例，供读者参考。

1. DBSCAN算法原理

1.1 基本概念定义

DBSCAN算法主要有两个参数：
领域半径：Eps；
成为核心对象的在领域半径内的最少点数：MinPts。
以上两个参数都会在下面的概念介绍中提到。

• Eps领域(Eps-neighborhood of a point)
  点p的Eps邻域，记为N_Eps（p），定义为N_Eps（p）= {q∈D | dist(p,q)≤Eps}。

• 核心对象 (core points)
  如果给定对象Eps领域内的样本点数大于等于MinPts，则称该对象为核心对象。

• 直接密度可达(directly density-reachable)
  若：
  1） p∈ N_Eps(q)
  2）|N_Eps(q)| ≥ MinPts
  则称对象p从核心对象q是直接密度可达的。

• 密度可达（density-reachable)
  对于对象p₁,p₂, …, p_n；
  令p₁= q, p_n = p。
  若p_i+1是从p_i直接密度可达的，则称p是从q密度可达的。

• 密度相连(density-connected)
  对于点p和点q，若点p点q都是从点o密度可达的，则称点p和点q密度相连。

• 簇(cluster)
  对于数据集D，若C是其中一个簇，C中的点需要满足以下两个条件：
  1）∀ p, q，如果 p∈ C且q 是从p密度可达的，则 q∈ C。
  2）∀ p, q ∈ C，p和q是密度相连的。

• 噪音(noise)
  不属于任何簇的点为噪音数据。

1.2 算法流程

• 1）给定领域半径：Eps和成为核心对象的在领域半径内的最少点数：MinPts。
• 2）从任意点p开始，将其标记为”visited“，检查其是否为核心点（即p的Eps邻域至少有MinPts个对象），如果不是核心点，则将其标记为噪声点。否则为p创建一个新的簇C，并且把把p的Eps邻域中的所有对象都放到候选集合N中。
• -3）迭代地把N中不属于其它簇的对象添加至C中，在此过程中，对于N中标记为”unvisited"的对象p‘，把它标记为“visited”，并且检查它的Eps邻域，如果p’也为核心对象，则p’的Eps邻域中的对象都被添加至N中。继续添加对象至C中，直到C不能扩展，即直到N为空。此时，簇C完全生成。
• 4）从剩余的对象中随机选择下一个未访问对象，重复3）的过程，直到所有对象都被访问。

2. 参数选择

2.1 领域半径：Eps的选取方法（k-distance函数）

• 1）选取k值，建议取k为2*维度-1。（其中维度为特征数）
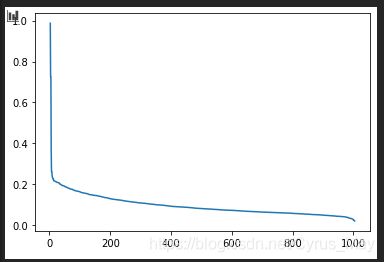
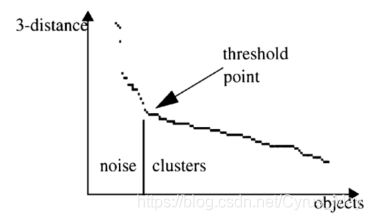
• 2） 计算并绘制k-distance图。（计算出每个点到距其第k近的点的距离，然后将这些距离从大到小排序后进行绘图。）
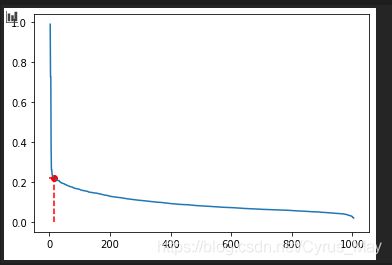
• 3）找到拐点位置的距离，即为Eps的值。
  如下图所示：
  

2.2 MinPts的选取方法

• MinPts的取值为上述k值加1，即：

$$MinPts=k+1$$

3. Python实现

链接: 参考我的另一篇博客.

4. 检测离群值的实例

4.1 导包及设置随机种子

import numpy as np
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN

np.random.seed(2021)

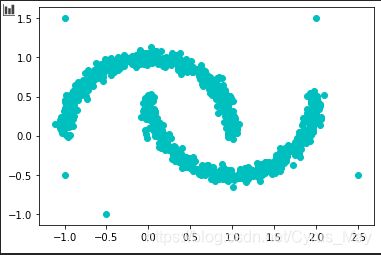
4.2 生成moon数据并绘图

data = np.ones([1005,2])
data[:1000] = make_moons(n_samples=1000,noise=0.05,random_state=2022)[0]
data[1000:] = [[-1,-0.5],
                [-0.5,-1],
                [-1,1.5],
                [2.5,-0.5],
                [2,1.5]]
print(data.shape)
plt.scatter(data[:,0],data[:,1],color="c")
plt.show()

4.3 选择参数

def select_MinPts(data,k):
    k_dist = []
    for i in range(data.shape[0]):
        dist = ((data[i] - data).sum(axis=1)**0.5)
        dist.sort()
        k_dist.append(dist[k])
    return np.array(k_dist)
k = 3  # 此处k取 2*2 -1 
k_dist = select_MinPts(data,k)
k_dist.sort()
plt.plot(np.arange(k_dist.shape[0]),k_dist[::-1])

有明显拐点

# 由拐点确定邻域半径
eps = k_dist[::-1][15]
plt.scatter(15,eps,color="r")
plt.plot([0,15],[eps,eps],linestyle="--",color = "r")
plt.plot([15,15],[0,eps],linestyle="--",color = "r")
plt.show()

4.4 建立聚类模型

dbscan_model = DBSCAN(eps=eps,min_samples=k+1)
label = dbscan_model.fit_predict(data)
print(label)

[ 0  0  0 ... -1 -1 -1]

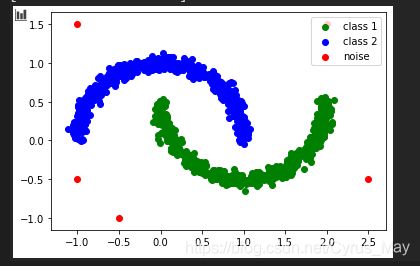
4.5 可视化展示

class_1 = []
class_2 = []
noise = []
for index,value in enumerate(label):
    if value == 0:
        class_1.append(index)
    elif value == 1:
        class_2.append(index)
    elif value == -1:
        noise.append(index)
plt.scatter(data[class_1,0],data[class_1,1],color="g",label="class 1")
plt.scatter(data[class_2,0],data[class_2,1],color="b",label = "class 2")
plt.scatter(data[noise,0],data[noise,1],color="r",label = "noise")
plt.legend()
plt.show()

by CyrusMay 2021 02 03

你和我背着空空的书包
逃出名为日常的监牢
忘了要长大
忘了要变老
忘了时间有脚
——————五月天（好好）——————