Nowcoder寒假算法基础集训营1
咕咕了好久，AC怪终于想起来WA补题了，log2r终于开始尝试写博客啦QAQ
（以下题目顺序为自己做题时体感难度排序 ）
F-对答案一时爽
Description
n n n道单选题，每题正确得 1 分，错误得0分。
已知两人每题的选项。求两人可能的最大得分和、最小得分和。
Solution
签到，最小得分为0，最大得分在所有题目两人中至少一人答案正确时取到。
#includeE-三棱锥之刻
Description
求一个球心在棱长为 a a a的正三棱锥中心，半径为 r r r的球与正三棱锥截交面的面积。
Solution
高中立体几何，所形成的四个截交面可能为空、圆、圆和正三角形截交、正三角形，分类讨论即可。
#includeB-括号
Description
构造非空括号字符串，恰好包含 k k k个不同合法括号对。
字符串长度 0 < l ≤ 1 e 5 , 0 ≤ k ≤ 1 e 9 0
Solution
1、 依次由 L L L个"(“和 R R R个”)“组成的字符串构成的不同合法括号对数目为 L × R L×R L×R。
2、 在上述序列中前 L L L个位置中第 m m m个位置插入一个”)"，构成的不同合法括号对数目为 L × R + m L×R+m L×R+m。
因此，只需找到 k = L × R + m ( m ≤ L , L + R + 1 ≤ 1 e 5 ) k=L×R+m(m≤L,L+R+1≤1e5) k=L×R+m(m≤L,L+R+1≤1e5)即可。
为使 L + R L+R L+R尽可能小，且 m ≤ L m≤L m≤L，可取：
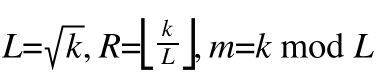
最后特判一下 k = 0 k=0 k=0的情况。
#includeI-限制不互素对的排列
Description
构造 1 ～ n 1～n 1～n的一种排列，使得恰好 k k k对相邻两数 g c d gcd gcd大于1。
2 ≤ n ≤ 1 e 5 ， 0 ≤ k ≤ n / 2 2≤n≤1e5，0≤k≤n/2 2≤n≤1e5，0≤k≤n/2。
Solution
1、 注意一下 k ≤ n / 2 k≤n/2 k≤n/2的条件，可以把 1 ～ n 1～n 1～n拆分成相邻偶数、相邻奇数和相邻整数。
2、 ( k + 1 ) (k+1) (k+1)个相邻偶数构成k个不互素对，而相邻奇数和相邻整数之间 g c d gcd gcd均为1。因此先放置(k+1)个偶数，再按顺序放置剩余的数即可。 k < n / 2 k
3、 若 k = n / 2 k=n/2 k=n/2，先按照 ( k − 1 ) (k-1) (k−1)的构造方式，然后取出排列中的6和3依次放到相邻偶数排列后，不互素对增加了1，构造完成。
4、 特判 n < 6 n<6 n<6的情况即可。
#includeA-串
Description
求长度不超过 n n n，由小写字母构成，删除或不删除部分字符后可得到"us"的字符串个数。
2 ≤ n ≤ 1 e 6 2≤n≤1e6 2≤n≤1e6，答案对 1 e 9 + 7 1e9+7 1e9+7取模。
Solution
递推， f [ i ] f[i] f[i]表示长度为 i i i且符合题意的字符串个数，考虑第 ( i + 1 ) (i+1) (i+1)位产生的方案数。
1、 当前i位符合题意时，第 ( i + 1 ) (i+1) (i+1)位随意填充，总方案数 26 × f [ i ] 26×f[i] 26×f[i]。
2、 考虑前i位不合题意，但前 ( i + 1 ) (i+1) (i+1)位符合题意。当且仅当前 i i i位含有’u’但不存在子序列"us"，且第 ( i + 1 ) (i+1) (i+1)位为’s’。前 i i i位含有"u"的字符串数目为 2 6 i − 2 5 i 26^i - 25^i 26i−25i，前 i i i位存在子序列的字符串数目为 f [ i ] f[i] f[i]。总方案数 2 6 i − 2 5 i − f [ i ] 26^i - 25^i-f[i] 26i−25i−f[i]。
因此，递推方程: f [ i + 1 ] = 25 × f [ i ] + 2 6 i − 2 5 i , f [ 2 ] = 1 f[i+1]=25×f[i]+26^i - 25^i,f[2]=1 f[i+1]=25×f[i]+26i−25i,f[2]=1
#includeJ-一群小青蛙呱蹦呱蹦呱
Description
长度为 n n n的格子里放无穷多青蛙，第 i i i只青蛙路线为以1为首项， p [ i ] p[i] p[i]为公比的等比数列，其中 p [ i ] p[i] p[i]为第 i i i大的素数，求 n n n个格子中所有未被占据格子编号的 l c m lcm lcm。
1 ≤ n ≤ 1.6 e 8 1≤n≤1.6e8 1≤n≤1.6e8，答案对 1 e 9 + 7 1e9+7 1e9+7取模。
Solution
对每个未被占据的格子进行质因数分解，考虑每个质因子对答案的贡献。
质因子对 l c m lcm lcm的贡献取决于质因子在未被占据的格子中最大次幂。
每个未被占据的格子均有至少两个质因子，因此，对于质因子2，其最大次幂为 l o g 2 [ n 3 ] log_2^{[\frac{n}{3}]} log2[3n]；对于其他质因子 p p p，其最大次幂为 l o g p [ n 2 ] log_p^{[\frac{n}{2}]} logp[2n]。
最终答案 2 l o g 2 [ n 3 ] ∏ i = 2 k ｜ p k ≤ n p i l o g p i [ n 2 ] 2^{log_{2}^{[\frac{n}{3}]}}\prod_{i=2}^{k｜p_k≤n} p_i^{log_{p_i}^{[\frac{n}{2}]}} 2log2[3n]∏i=2k｜pk≤npilogpi[2n]
（有被题目名称可爱到）
#includeC-红和蓝
Description
给定一颗树，对树的节点 1 ～ n 1～n 1～n染红色或蓝色，使得红色节点相邻节点有且仅有一个红色节点；蓝色节点相邻节点有且仅有一个蓝色节点。
1 ≤ n ≤ 1 e 5 1≤n≤1e5 1≤n≤1e5
Solution
1、 叶节点与其父节点为同色。
2、 叶节点的父节点与其父节点的父节点为异色。
3、 若将叶节点及其父节点删除，则其父节点的父节点成为新的叶节点，新叶节点必与新叶节点的父节点同色。
因此，对于任意一个节点，当且仅当节点数目为奇数的子树个数 ≤ 1 ≤1 ≤1时，该节点可以被染色。且该节点与其父节点颜色相反当且仅当该节点子树大小为奇数。
首先第一遍dfs预处理出以每个节点为根的子树大小，顺带判断无解的情况，然后第二遍dfs从根节点进行染色。
#includeD-点一成零
Description
给定 n × n n×n n×n的 0 − 1 0-1 0−1方阵，每次操作把一个元素均为"1"的连通块变为元素均为"0"， k k k次询问，每次询问把方阵中的某个元素变为"1"，求每次询问后把方阵变为0方阵的方案数。
n ≤ 500 ， k ≤ 1 e 5 n≤500，k≤1e5 n≤500，k≤1e5，强制在线。
Solution
并查集维护每个连通块大小。设连通块数目为 N N N，第 i i i个连通块大小为 s i z e i size_i sizei，则方案数为 N ! ∏ i = 1 N s i z e i N!\prod_{i=1}^{N} size_i N!∏i=1Nsizei，每次查询时更新连通块大小及数目。
#include 还剩下两道题，一道不会的数学和一道大模拟。好像挺心把的（但不影响2048好玩hhh），应该有时间也不会去写了，以上。
