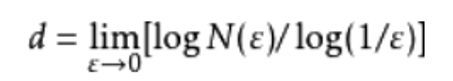直观理解图像的分形维数附matlab实现

纹理粗糙度是图像的重要视觉特征，对图像的分析、识别和解释有着重要的意义。人们在纹理分析方面作了大量的研究工作，提出了许多纹理粗糙度的测量和描述方法。分形理论指出大多数自然物体表面在空间上都是分形的[1]，而且这些表面的灰度图像也是分形的，这为分形模型在图像分析领域的应用提供了理论基础。而纹理粗糙度的描述大多采用分形维数法。分形维数是图像稳定性的表示量，可以用来描述图像表面的粗糙程度。关于分形其实是一个十分有趣的理论，分形绘制的图案都十分漂亮感兴趣的同学可以看看：传送门；下面通过一些例子直观理解图像的分形维数，不涉及太多深奥的理论。

1、图像灰度表面

function Show_GraySurface(filename)
%   把一幅图像看成三维空间的曲面，
%   像素的位置(x,y)构成xoy坐标面，
%   像素的灰度值看成z轴的值由此构成灰度曲面
    picture_dir = 'E:\image-processing\featuer_lesson\Differential_Box-counting\DBC_test_picture\';
    I = imread([picture_dir,filename]);
        if (length(size(I)) > 2)
            I = rgb2gray(I);
        end 
    M = size(I,1);
    Temp = diag([1:256])*ones(256,256);
    x = reshape(Temp.',1,M*M);
    y = reshape(Temp,1,M*M);
    z = reshape(I,1,M*M);
    tri = delaunay(x,y);
    trisurf(tri,x,y,z);
    shading interp
    view(3);grid on;colorbar
end

图（1） matlab画出图像的灰度曲面

 

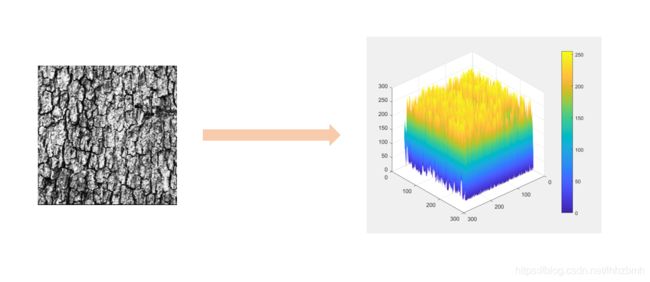
matlab运行上述代码就可以画出图像的灰度曲面，把一幅图像放置在xoy平面上，像素的灰度值作为z轴上的值，由此构成的曲面叫做图像的灰度曲面。把代码里面的picture_dir改成自己图片的目录，直接运行Show_GraySurface('filename')就可以看见结果。注意输入图片的大小是256x256的。

 2、计算图像分形维数——差分盒子维 DBC（diflerential box-counting）

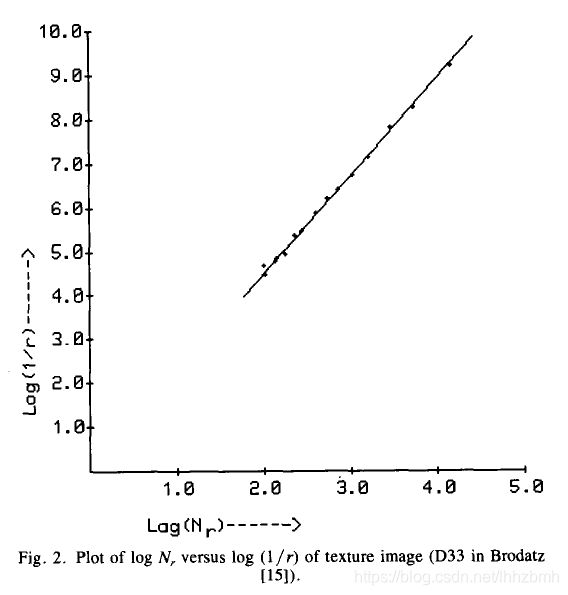
图（1）中的图片是Brodatz纹理集中的一张图片，人眼直观上看可以很容易知道这是一张树皮的照片，并根据自己的经验能给出这个树皮面很粗糙的评价，但是计算机如何评价一张图片的粗糙程度呢？本章介绍的分形维数就是评价图像粗糙程度的一个度量。Matlab程序描绘的灰度曲面中，蓝色向黄色变化的过程就是灰度值从小到大变化的过程，我们可以根据颜色判断灰度曲面上对应灰度值的大小。假如我们从灰度曲面的正上方俯视，看到的结果应该与原图一致，读者可以自己实验一下从不同角度观察这个平面，但是我们从侧面观察就能发现灰度曲面的复杂性，曲面上有很多黄色的“山峰”，也有很多蓝色的“谷底”纵横交错，看起来已经不像是一个曲面了，这里表现出一些分形的特征比如自相似性，分形维数度量图像的粗糙程度，就是度量图像灰度曲面的复杂程度，分形维数越高代表曲面越复杂，图像也就越粗糙。下面给出一个笔者自己实现的计算图像盒子维的代码，参考论文[2]，论文传送门。

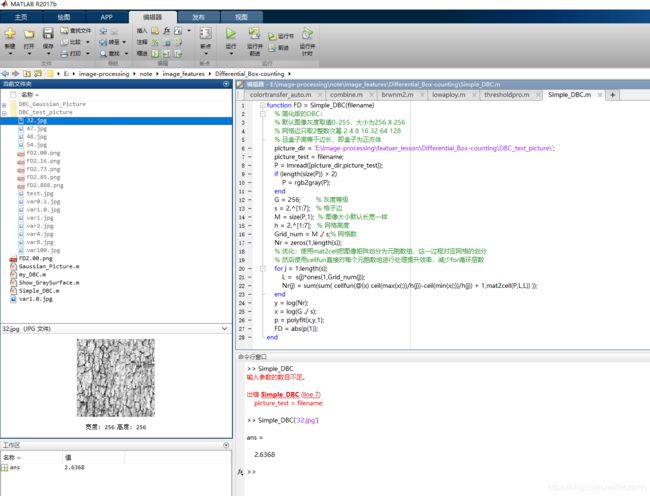
function FD = Simple_DBC(filename)
    % 简化版的DBC：
    % 默认图像灰度取值0-255，大小为256 X 256
    % 网格边只取2整数次幂 2 4 8 16 32 64 128 
    % 且盒子高等于边长，即盒子为正方体
    picture_dir = 'E:\image-processing\featuer_lesson\Differential_Box-counting\DBC_test_picture\';
    picture_test = filename;
    P = imread([picture_dir,picture_test]);
    if (length(size(P)) > 2)
        P = rgb2gray(P);
    end 
    G = 256;        % 灰度等级
    s = 2.^[1:7];   % 格子边
    M = size(P,1);  % 图像大小默认长宽一样
    h = 2.^[1:7];   % 网格高度
    Grid_num = M ./ s;% 网格数
    Nr = zeros(1,length(s));
    % 优化：使用mat2cell把图像矩阵划分为元胞数组，这一过程对应网格的划分
    % 然后使用cellfun直接对每个元胞数组进行处理提升效率，减少for循环层数
    for j = 1:length(s);
        L =  s(j)*ones(1,Grid_num(j));  
        Nr(j) = sum(sum( cellfun(@(x) ceil(max(x(:))/h(j))-ceil(min(x(:))/h(j)) + 1,mat2cell(P,L,L)) ));
    end
    y = log(Nr);
    x = log(G ./ s);
    p = polyfit(x,y,1);
    FD = abs(p(1));
end

为了理解上面的程序，需要简单介绍一下分形维数的性质；

计算公式

直接用公式求解很难计算，差分盒子维采用下面的思路进行计算。假设有一个边长为的立方体盒子，用这个盒子去度量我们的图形。 

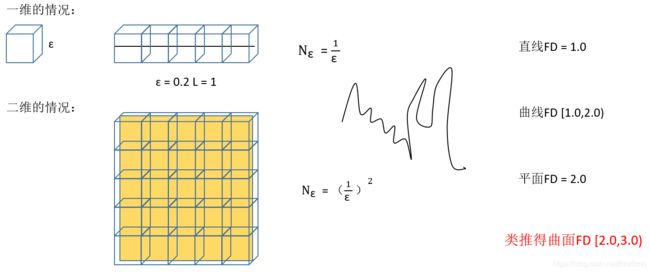
• 直线的时候，设直线长度L=1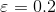，，那么需要5个盒子就可以覆盖整条直线，需要的盒子数（N）和的关系为：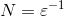
• 平面的时候，设边长a=1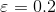，，那么需要25个盒子就可以覆盖整个正方形，需要的盒子数（N）和的关系为：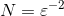
• 推论当维数d确定以后，需要的盒子数（N）和的关系为：

分形维数的性质

 

 由上面的图我们可以猜测，弯弯曲曲的曲线，相比直线需要更多的盒子才能覆盖，但是肯定少于覆盖平面所需的盒子，所以曲线的分形维数取值区间为[1.0,2.0)；类似得到曲面的分形维数取值区间为[2.0,3.0)。程序计算出来的分形维数必须落在这个区间内。受到上面思路的启发，可以用一个个盒子去度量图形灰度曲面的分形维数。

差分盒子维的计算（论文截图）

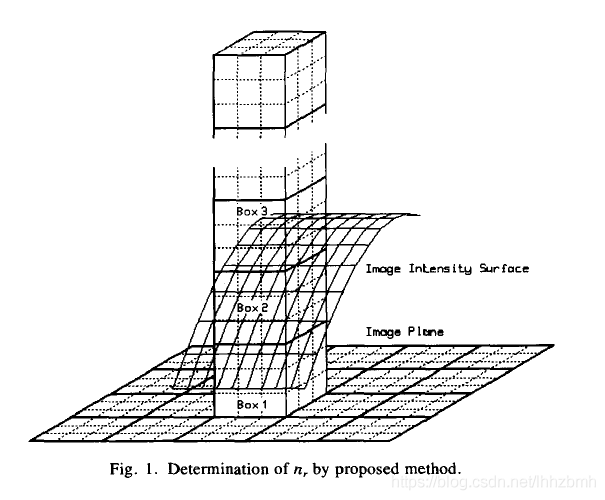
 把图像放置在平面（image plane）上，构成的灰度曲面（Image Instensity surface）如上图所示，然后把下面的平面用网格进行划分，然后用不同大小的盒子去“覆盖”图像的灰度平面。上图中盒子的边长为3，网格为3X3，在图示的网格内共需要三个盒子才能覆盖该区域内的灰度曲面记作，然后计算整个灰度曲面共需要多少个盒子才能覆盖这个曲面；然后再换不同大小的网格，重复上述过程。程序为了实现简单网格大小取了2的整数次幂，输入的图像大小256X256，也是为了便于计算。有兴趣的可以改进一下。

拟合直线斜率得到FD（论文截图）

 

 对公式两边取对数得到：，然后取不同的值，得到不同的N，然后用最小二乘法拟合，得到d。（论文的字母和这里的字母略有不同）

3、实验结果：

数值均在预期范围，和其他方法对比，其FD大小关系也是正确的，和人眼的感官一致（左边的图明显感觉纹理比右图粗糙）。

用到的测试图像：

小结

参考资料：

[1] B. B. Mandelbrot, Fractal Geometry of Nature. San Francisco: Freeman, 1982.

[2]N. Sarkar and B. B. Chaudhuri, "An efficient differential box-counting approach to compute fractal dimension of image," in IEEE Transactions on Systems, Man, and Cybernetics, vol. 24, no. 1, pp. 115-120, Jan. 1994.

-------------------------------------------------------------------分割线---------------------------------------------------------------------------------------------

有同学试着运行，但是不成功的，注意把图片目录的路径换一下，另外这个实现很简单，没有考虑图片的大小，只能处理256x256大小的图片，有能力的可以再优化一下，用于测试的图片在上面放出来了。