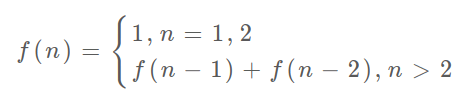文章首发于公众号 宫水三叶的刷题日记,转载请联系开白名单。
前言
在系统学习动态规划之前,一直搞不懂「动态规划」和「记忆化搜索」之间的区别。
总觉得动态规划只是单纯的难在于对“状态”的抽象定义和“状态转移方程”的推导,并无具体的规律可循。
本文将助你彻底搞懂动态规划。点击 这里 可以查看更多算法面试相关内容~
演变过程
暴力递归 -> 记忆化搜索 -> 动态规划
其实动态规划也就是这样演练过来的。
可以说几乎所有的「动态规划」都可以通过「暴力递归」转换而来,前提是该问题是一个“无后效性”问题。
无后效性
所谓的“无后效性”是指:当某阶段的状态一旦确定,此后的决策过程和最终结果将不受此前的各种状态所影响。可简单理解为当编写好一个递归函数之后,当可变参数确定之后,结果是唯一确定的。
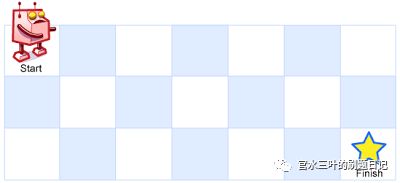
可能你还是对什么是“无后效性”问题感到难以理解。没关系,我们再举一个更具象的例子,这是 LeetCode 62. Unique Paths :给定一个 m x n 的矩阵,从左上角作为起点,到达右下角共有多少条路径(机器人只能往右或者往下进行移动)。
这是一道经典的「动态规划」入门题目,也是一个经典的“无后效性”问题。
它的“无后效性”体现在:当给定了某个状态(一个具体的 m x n 的矩阵和某个起点,如 (1,2)),那么从这个点到达右下角的路径数量就是完全确定的。
而与如何到达这个“状态”无关,与机器人是经过点 (0,2) 到达的 (1,2),还是经过 (1,1) 到达的 (1,2) 无关。
这就是所谓的“无后效性”问题。
当我们尝试使用「动态规划」解决问题的时候,首先要关注该问题是否为一个“无后效性”问题。
1:暴力递归
经常我们面对一个问题,即使我们明确知道了它是一个“无后效性”问题,它可以通过「动态规划」来解决。我们还是觉得难以入手。
这时候我的建议是,先写一个「暴力递归」的版本。
还是以刚刚说到的 LeetCode 62. Unique Paths 举例:
class Solution {
public int uniquePaths(int m, int n) {
return recursive(m, n, 0, 0);
}
private int recursive(int m, int n, int i, int j) {
if (i == m - 1 || j == n - 1) return 1;
return recursive(m, n, i + 1, j) + recursive(m, n, i, j + 1);
}
} 当我还不知道如何使用「动态规划」求解时,我会设计一个递归函数 recursive() 。
函数传入矩阵信息和机器人当前所在的位置,返回在这个矩阵里,从机器人所在的位置出发,到达右下角有多少条路径。
有了这个递归函数之后,那问题其实就是求解 recursive(m, n, 0, 0):求解从 (0,0) 到右下角的路径数量。
接下来,实现这个函数:
- Base case: 由于题目明确了机器人只能往下或者往右两个方向走,所以可以定下来递归方法的 base case 是当已经处于矩阵的最后一行或者最后一列,即只一条路可以走。
- 其余情况:机器人既可以往右走也可以往下走,所以对于某一个位置来说,到达右下角的路径数量等于它右边位置到达右下角的路径数量 + 它下方位置到达右下角的路径数量。即
recursive(m, n, i + 1, j) + recursive(m, n, i, j + 1),这两个位置都可以通过递归函数进行求解。
其实到这里,我们已经求解了这个问题了。
但这种做法还有个严重的性能问题。
2:记忆化搜索
如果将我们上述的代码提交到 LeetCode,会得到 timeout 的结果。
可见「暴力递归」的解决方案“很慢”。
我们知道所有递归函数的本质都是“压栈”和“弹栈”。
既然这个过程很慢,我们可以通过将递归版本暴力解法的改为非递归的暴力解法,来解决 timeout 的问题吗?
答案是不行,因为导致 timeout 的原因不在于使用“递归”手段所带来的成本。
而在于在计算过程,我们进行了多次的重复计算。
我们尝试展开递归过程第几步来看看:
不难发现,在递归展开过程会遇到很多的重复计算。
随着我们整个递归过程的展开,重复计算的次数会呈倍数增长。
这才是「暴力递归」解决方案“慢”的原因。
既然是重复计算导致的 timeout,我们自然会想到将计算结果进行“缓存”的方案:
class Solution {
private int[][] cache;
public int uniquePaths(int m, int n) {
cache = new int[m][n];
for (int i = 0; i < m; i++) {
int[] ints = new int[n];
Arrays.fill(ints, -1);
cache[i] = ints;
}
return recursive(m, n, 0, 0);
}
private int recursive(int m, int n, int i, int j) {
if (i == m - 1 || j == n - 1) return 1;
if (cache[i][j] == -1) {
if (cache[i + 1][j] == -1) {
cache[i + 1][j] = recursive(m, n, i + 1, j);
}
if (cache[i][j + 1] == -1) {
cache[i][j + 1] = recursive(m, n, i, j + 1);
}
cache[i][j] = cache[i + 1][j] + cache[i][j + 1];
}
return cache[i][j];
}
} 对「暴力递归」过程中的中间结果进行缓存,确保相同的情况只会被计算一次的做法,称为「记忆化搜索」。
做了这样的改进之后,提交 LeetCode 已经能 AC 并得到一个不错的评级了。
我们再细想一下就会发现,其实整个求解过程,对于每个情况(每个点)的访问次数并没有发生改变。
只是从「以前的每次访问都进行求解」改进为「只有第一次访问才真正求解」。
事实上,我们通过查看 recursive() 方法就可以发现:
当我们求解某一个点 (i, j) 的答案时,其实是依赖于 (i, j + 1) 和 (i + 1, j) 。
也就是每求解一个点的答案,都需要访问两个点的结果。
这种情况是由于我们采用的是“自顶向下”的解决思路所导致的。
我们无法直观确定哪个点的结果会在什么时候被访问,被访问多少次。
所以我们不得不使用一个与矩阵相同大小的数组,将所有中间结果“缓存”起来。
换句话说,「记忆化搜索」解决的是重复计算的问题,并没有解决结果访问时机和访问次数的不确定问题。
2.1:次优解版本的「记忆化搜索」
关于「记忆化搜索」最后再说一下。
网上有不少博客和资料在编写「记忆化搜索」解决方案时,会编写类似如下的代码:
class Solution {
private int[][] cache;
public int uniquePaths(int m, int n) {
cache = new int[m][n];
for (int i = 0; i < m; i++) {
int[] ints = new int[n];
Arrays.fill(ints, -1);
cache[i] = ints;
}
return recursive(m, n, 0, 0);
}
private int recursive(int m, int n, int i, int j) {
if (i == m - 1 || j == n - 1) return 1;
if (cache[i][j] == -1) {
cache[i][j] = recursive(m, n, i + 1, j) + recursive(m, n, i, j + 1);
}
return cache[i][j];
}
} 可以和我上面提供的解决方案作对比。主要区别在于 if (cache[i][j] == -1) 的判断里面。
在我提供解决方案中,会在计算 cache[i][j] 时,尝试从“缓存”中读取 cache[i + 1][j] 和 cache[i][j + 1],确保每次调用 recursive() 都是必须的,不重复的。
网上大多数的解决方案只会在外层读取“缓存”,在真正计算 cache[i][j] 的时候并不采取先检查再调用的方式,直接调用 recursive() 计算子问题 。
虽然两者相比与直接的「暴力递归」都大大减少了计算次数(recursive() 的访问次数),但后者的计算次数显然要比前者高上不少。
你可能会觉得反正都是“自顶向下”,两者应该没有区别吧?
为此我提供了以下实验代码来比较它们对 recursive() 的调用次数:
class Solution {
public static void main(String[] args) {
Solution solution = new Solution();
solution.uniquePaths(15, 15);
}
private int[][] cache;
private long count; _// 统计 递归函数 的调用次数_
public int uniquePaths(int m, int n) {
cache = new int[m][n];
for (int i = 0; i < m; i++) {
int[] ints = new int[n];
Arrays.fill(ints, -1);
cache[i] = ints;
}
_// int result = recursive(m, n, 0, 0); // count = 80233199_
_// int result = cacheRecursive(m, n, 0, 0); // count = 393_
int result = fullCacheRecursive(m, n, 0, 0); _// count = 224_
System.out.println(count);
return result;
}
_// 完全缓存_
private int fullCacheRecursive(int m, int n, int i, int j) {
count++;
if (i == m - 1 || j == n - 1) return 1;
if (cache[i][j] == -1) {
if (cache[i + 1][j] == -1) {
cache[i + 1][j] = fullCacheRecursive(m, n, i + 1, j);
}
if (cache[i][j + 1] == -1) {
cache[i][j + 1] = fullCacheRecursive(m, n, i, j + 1);
}
cache[i][j] = cache[i + 1][j] + cache[i][j + 1];
}
return cache[i][j];
}
_// 只有外层缓存_
private int cacheRecursive(int m, int n, int i, int j) {
count++;
if (i == m - 1 || j == n - 1) return 1;
if (cache[i][j] == -1) {
cache[i][j] = cacheRecursive(m, n, i + 1, j) + cacheRecursive(m, n, i, j + 1);
}
return cache[i][j];
}
_// 不使用缓存_
private int recursive(int m, int n, int i, int j) {
count++;
if (i == m - 1 || j == n - 1) return 1;
return recursive(m, n, i + 1, j) + recursive(m, n, i, j + 1);
}
} 因为我们使用 cache 数组的目的是减少 recursive() 函数的调用。
只有确保在每次调用 recursive() 之前先去 cache 数组检查,我们才可以将对 recursive() 函数的调用次数减到最少。
在数据为 15 的样本下,这是 O(393n) 和 O(224n) 的区别,但对于一些卡常数特别严重的 OJ,尤其重要。
所以我建议你在「记忆化搜索」的解决方案时,采取与我一样的策略:
确保在每次访问递归函数时先去“缓存”检查。尽管这有点“不美观”,但它能发挥「记忆化搜索」的最大作用。
3:从「自顶向下」到「自底向上」
你可能会想,为什么我们需要改进「记忆化搜索」,为什么需要明确中间结果的访问时机和访问次数?
因为一旦我们能明确中间结果的访问时机和访问次数,将为我们的算法带来巨大的提升空间。
前面说到,因为我们无法确定中间结果的访问时机和访问次数,所以我们不得不“缓存”全部中间结果。
但如果我们能明确中间结果的访问时机和访问次数,至少我们可以大大降低算法的空间复杂度。
这就涉及解决思路的转换:从「自顶向下」到「自底向上」 。
如何实现从「自顶向下」到「自底向上」的转变,还是通过具体的例子来理解。
这是 LeetCode 509. Fibonacci Number,著名的“斐波那契数列”问题。
如果不了解什么是“斐波那契数列”,可以查看对应的 维基百科。
由于斐波那契公式为:
天然适合使用递归:
public class Solution {
private int[] cache;
public int fib(int n) {
cache = new int[n + 1];
return recursive(n);
}
private int recursive(int n) {
if (n <= 1) return n;
if (n == 2) return 1;
if (cache[n] == 0) {
if (cache[n - 1] == 0) {
cache[n - 1] = recursive(n - 1);
}
if (cache[n - 2] == 0) {
cache[n - 2] = recursive(n - 2);
}
cache[n] = cache[n - 1] + cache[n - 2];
}
return cache[n];
}
} 但这仍然会有我们之前所说的问题,这些问题都是因为直接递归是“自顶向下”所导致的。
这样的解法的时空复杂度为 O(n) :每个值计算一次,使用了长度为 n + 1 的数组。
通过观察斐波那契公式,我们可以发现要计算某个 n ,只需要知道 n - 1 的解和 n - 2 的解。
同时 n = 1 和 n = 2 的解又是已知的(base case)。
所以我们大可以从 n = 3 出发,逐步往后迭代得出 n 的解。
由于计算某个值的解,只依赖该值的前一位的解和前两位的解,所以我们只需要使用几个变量缓存最近的中间结果即可:
class Solution {
public int fib(int n) {
if (n <= 1) return n;
if (n == 2) return 1;
int prev1 = 1, prev2 = 1;
int cur = prev1 + prev2;
for (int i = 3; i <= n; i++) {
cur = prev1 + prev2;
prev2 = prev1;
prev1 = cur;
}
return cur;
}
} 这样我们就把原本空间复杂度为 O(N) 的算法降低为 O(1) :只是用了几个有限的变量。
但不是所有的「动态规划」都像“斐波那契数列”那么简单就能实现从“自顶向下”到“自底向上”的转变。
当然也不是毫无规律可循,尤其是我们已经写出了「暴力递归」的解决方案。
让我们再次回到 LeetCode 62. Unique Paths 当中:
class Solution {
public int uniquePaths(int m, int n) {
_// 由于我们的「暴力递归」函数,真正的可变参数就是 i 和 j( 变化范围分别是 [0,m-1] 和 [0, n-1] )_
_// 所以建议一个二维的 dp 数组进行结果存储(相当于建一个表格)_
int[][] dp = new int[m][n];
_// 根据「暴力递归」函数中的 base case_
_// 我们可以直接得出 dp 中最后一行和最后一列的值(将表格的最后一行和最后一列填上)_
for (int i = 0; i < n; i++) dp[m - 1][i] = 1
for (int i = 0; i < m; i++) dp[i][n - 1] = 1;
_// 根据「暴力递归」函数中对其他情况的处理逻辑(依赖关系)编写循环_
_//(根据表格的最后一行和最后一列的值,得出表格的其他格子的值)_
for (int i = m - 2; i >= 0; i--) {
for (int j = n - 2; j >= 0; j--) {
dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
}
}
_// 最终我们要的是 dp[0][0](表格中左上角的位置,也就起点的值)_
return dp[0][0];
_// 原「暴力递归」调用_
_// return recursive(m, n, 0, 0);_
}
private int recursive(int m, int n, int i, int j) {
_// base case_
if (i == m - 1 || j == n - 1) return 1;
_// 其余情况_
return recursive(m, n, i + 1, j) + recursive(m, n, i, j + 1);
}
} 不难发现,我们甚至可以直接根据「暴力递归」来写出「动态规划」,而不需要关心原问题是什么。
简单的「动态规划」其实就是一个“打表格”的过程:
先根据 base case 定下来表格中的一些位置的值,再根据已得出值的位置去推算其他格子的信息。
推算所用到的依赖关系,也就是我们「暴力递归」中的“其余情况”处理逻辑。
动态规划的本质
动态规划的本质其实仍然是枚举:枚举所有的方案,并从中找出最优解。
但和「暴力递归」不同的是,「动态规划」少了很多的重复计算。
因为所依赖的这些历史结果,都被存起来了,因此节省了大量重复计算。
从这一点来说,「动态规划」和「记忆化搜索」都是类似的。
要把历史结果存起来,必然要使用数据结构,在 dp 中我们通常使用一维数组或者二维数据来存储,假设是 dp[]。
那么对应解 dp 问题我们有以下过程
状态定义: 确定 dp[] 中元素的含义,也就是说需要明确 dp[i] 是代表什么内容状态转移:确定 dp[] 元素之间的关系,dp[i] 这个格子是由哪些 dp 格子推算而来的。如斐波那契数列中就有 dp[i] = dp[i - 1] + dp[i - 2]起始值:base case,dp[] 中的哪些格子是可以直接得出结果的。如斐波那契数列中就有 dp[0] = 0 和 dp[1] = 1
-
- *
消除“后效性”
我们知道使用「动态规划」的前提是问题的“无后效性” 。
但是有些时候问题的“无后效性” 并不容易体现。
需要我们多引入一维来进行“消除”。
例如 LeetCode 上经典的「股票问题」,使用动态规划求解时往往需要多引入一维表示状态,有时候甚至需要再引入一维代表购买次数。
注意这里说的消除是带引号的,其实这样的做法更多的是作为一种“技巧”,它并没有真正改变问题“后效性” ,只是让问题看上去变得简单的。
由于本文篇幅已经很长了,这里就不再展开「股票问题」。
之后会使用专门章节来对「股票问题」进行讲解,以达到使用同一思路解决所有「股票问题」的目的,敬请期待。
总结
到这里我们已经可以回答「动态规划」和「记忆化搜索」的区别是什么了。
「记忆化搜索」本质是带“缓存”功能的「暴力递归」:
它只能解决重复计算的问题,而不能确定中间结果的访问时机和访问次数,本质是一种“自顶向下”的解决方式。
「动态规划」是一种“自底向上”的解决方案 :
能明确访问时机和访问次数,这为降低算法的空间复杂度带来巨大空间,我们可以根据依赖关系来决定保留哪些中间结果,而无须将全部中间结果进行“缓存”。