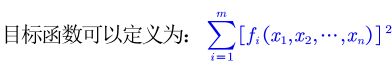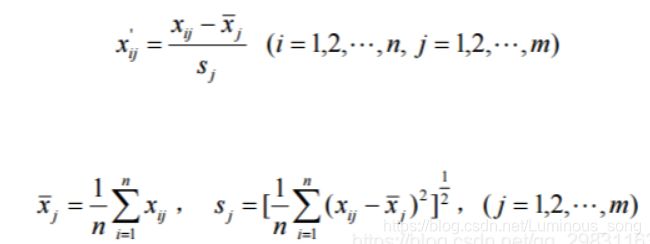数学建模算法体系分类

数据预处理模型

插值拟合

主要用于对数据的补全处理
其中样本点较少时（泛指样本点小于30个）采用插值方法，主要有拉格朗日插值算法、牛顿插值、双线性内插和双三次插值
样本点较多时（大于30个）则采用拟合函数

插值

拉格朗日插值法

龙格现象：在两端处波动极大，产生明显的震荡，不要轻易使用高次插值

分段线性插值

选取跟节点x最近的三个节点Xi-1，Xi，Xi+1进行二次插值

牛顿插值

埃尔米特（Hermite）插值

分段三次Hermite插值多项式

p = pchip(x,y,new_x);

三次样条插值

p = spline(x,y,new_x)

n维数据插值

p = interpn(x1,x2,…,xn,y,new_x1,new_x2,…,new_xn.method);
//x1，x2是已知样本点的横坐标
//y是已知样本点的纵坐标
//method：‘linear’，‘cubic’，‘spline’，‘nearest’

拟合

拟合得到的是一条曲线

最小二乘法

评价

评价拟合的好坏：
拟合优度R^2：只能在拟合函数是线性函数时作为参数 R² = SSR/SST,R²越接近1，说明拟合越好
总体平方和SST：SST = SSE+SSR
回归平方和SSE：当拟合函数是线性函数或其他函数时可以只看SSE
残差平方和SSR

拟合工具箱

cftool：最多是三维

主成分分析

主要用于多维数据的降维处理，减少数据冗余等
能将多个指标转换为少数几个主成分，这些主成分是原始变量的线性组合，且彼此之间互不相关，能反映出原始数据的大部分信息。
适用场景：问题涉及到多变量且变量之间存在很强的相关性时，可以考虑使用主成分分析的方法来对数据进行简化。


过程：

1. 首先对其进行标准化处理
   
2. 计算标准化样本的协方差矩阵（一般是相关系数矩阵）
   
3. 计算R的特征值和特征向量
4. 计算主成分贡献率和累计贡献率
   
5. 写出主成分：一般取累计贡献率超过80%的特征值所对应的第一、第二、…、第m个主成分
   
6. 根据系数分析主成分代表的意义：指标前面的系数越大，代表该指标对于该主成分的影响越大
7. 应用：主成分可用于聚类分析，可用于回归分析
   主成分分析要好好解释每个主成分的意义

clear;clc
%  load data1.mat   % 主成分聚类
 load data2.mat   % 主成分回归

% 注意，这里可以对数据先进行描述性统计
% 描述性统计的内容见第5讲.相关系数
[n,p] = size(x);  % n是样本个数，p是指标个数

%% 第一步：对数据x标准化为X
X=zscore(x);   % matlab内置的标准化函数（x-mean(x)）/std(x)

%% 第二步：计算样本协方差矩阵
R = cov(X);

%% 注意：以上两步可合并为下面一步：直接计算样本相关系数矩阵
R = corrcoef(x);
disp('样本相关系数矩阵为：')
disp(R)

%% 第三步：计算R的特征值和特征向量
% 注意：R是半正定矩阵，所以其特征值不为负数
% R同时是对称矩阵，Matlab计算对称矩阵时，会将特征值按照从小到大排列哦
% eig函数的详解见第一讲层次分析法的视频
[V,D] = eig(R);  % V 特征向量矩阵  D 特征值构成的对角矩阵


%% 第四步：计算主成分贡献率和累计贡献率
lambda = diag(D);  % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1);  % 因为lambda向量是从小大到排序的，我们将其调个头
contribution_rate = lambda / sum(lambda);  % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda);   % 计算累计贡献率  cumsum是求累加值的函数
disp('特征值为：')
disp(lambda')  % 转置为行向量，方便展示
disp('贡献率为：')
disp(contribution_rate')
disp('累计贡献率为：')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为：')
% 注意：这里的特征向量要和特征值一一对应，之前特征值相当于颠倒过来了，因此特征向量的各列需要颠倒过来
%  rot90函数可以使一个矩阵逆时针旋转90度，然后再转置，就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)


%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数:  ');
F = zeros(n,m);  %初始化保存主成分的矩阵（每一列是一个主成分）
for i = 1:m
    ai = V(:,i)';   % 将第i个特征向量取出，并转置为行向量
    Ai = repmat(ai,n,1);   % 将这个行向量重复n次，构成一个n*p的矩阵
    F(:, i) = sum(Ai .* X, 2);  % 注意，对标准化的数据求了权重后要计算每一行的和
end

%% (1)主成分聚类 ： 将主成分指标所在的F矩阵复制到Excel表格，然后再用Spss进行聚类
% 在Excel第一行输入指标名称（F1,F2, ..., Fm）
% 双击Matlab工作区的F,进入变量编辑中，然后复制里面的数据到Excel表格
% 导出数据之后，我们后续的分析就可以在Spss中进行。

%%（2）主成分回归：将x使用主成分得到主成分指标，并将y标准化，接着导出到Excel，然后再使用Stata回归
% Y = zscore(y);  % 一定要将y进行标准化哦~
% 在Excel第一行输入指标名称（Y,F1, F2, ..., Fm）
% 分别双击Matlab工作区的Y和F,进入变量编辑中，然后复制里面的数据到Excel表格
% 导出数据之后，我们后续的分析就可以在Stata中进行。

聚类分析

主要用于分析诊断数据异常值并进行剔除
适用于空间分布的大样本/小样本异常值监测

均值、方差分析、协方差分析等统计方法

主要用于数据的截取或特征选择等
spss中描述性分析

优化模型

三要素：

1. 决策变量
   通过变量的改变，获得更好的结果
   可以理解为控制变量，或者是一些决定性的参数
2. 目标函数
   所求：评价是都想着好的方向发展，用来评测的标准
3. 约束
   限定了决策变量的具体的设置范围一个定义域的限定

分类

• 单目标优化：评测目标只有一个，只需要根据具体的约束条件，求得最值
  适用场景：针对问题所建立的优化目标函数有且只有一个
• 多目标优化：多个评测函数的存在，而且使用不同的评测函数的解也是不同的。目标函数不唯一
  适用场景：基于问题所构建的优化目标函数不唯一，常出现在金融投资领域，往往要求风险更小，收益更大
• 线性规划：目标函数和约束条件都是线性的
• 非线性规划：在目标函数和约束条件中只要有一个是非线性函数都是非线性规划
• 整数规划：规划中的决策变量都是整数
• 二次规划：目标函数是二次的，约束条件是线性的
• 动态规划：基本思想是将待求问题问题分解为若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解
  适用场景：背包问题、运输问题、分割问题
• 图论模型：
  - 最短路模型：Dijkstra算法和Floyd算法（求解任意两个节点间的距离），用于求解两点间的最短距离。路径规划问题（修建道路，设定救援路线等）
  - 最大流模型：道路可承载的最大车流量。企业生产运输问题、交通拥堵优化问题
  - 最小生成树：包含所有顶点。道路规划、通讯网络规划、管道铺设、电线布设等
  - 排队论模型：商店购货、轮船进港、病人就诊等

目标规划

多目标规划

若一个规划问题中有多个目标，对多目标函数进行加权组合，使问题变为单目标规划，然后利用之前学的知识进行求解。
注意：

1. 要先将多个目标函数统一为最大化或最小化问题后才可以进行加权组合
2. 如果量纲不同，需要对其进行标准化后再进行加权（标准化的方法：用目标函数除以某一个常量，该常量是这个目标函数的某个值）
3. 对多目标函数进行加权求和时，权重需要由该问题领域的专家给定，无特殊说明，可令权重相同
4. 要对结果进行敏感性分析，通过逐一改变相关变量数值的方法来解释关键指标受这些因素变动影响大小的规律

线性规划

在matlab中默认求最小值，且不等式约束都是小于等于

线性规划

线性规划问题是在一组线性约束条件的限制下，求一线性目标函数最大或最小值的问题

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)
//f：目标函数（决策变量前面的系数对应的矩阵）
//A，b：对应线性不等式约束
//Aeq，beq：对应线性等式约束
//lb，ub分别对应决策向量的下界向量和上界向量
[k,fval] = fminsearch(@Obj_fun,k0);
//Nelder-Mead单纯形法求最小值，适用于解决不可导或求导复杂的函数优化问题
[k,fval] = fminunc(@Obj_fun,k0)
//拟牛顿法求解无约束最小值，适用于解决容易求导的函数优化问题

很多看其实不是线性规划的问题，也可以通过变换转化为线性规划的问题来解决
min |x1|+|x2|+…+|xn|
xi = ui-vi |xi| = ui+vi
ui = (xi+|xi|)/2 vi = (|xi|-xi)/2
min c^y,
s.t. [A,-A][u,v]’<=b
求得解为u，v
x = u-v

整数规划

数学规划中的变量限制为整数时，称为整数规划

[x,favl] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
//intcon可以指定哪些决策变量是整数

0-1规划

决策变量只能取0或1
一般用于相互排斥的约束条件，指派问题等

非线性规划

[x,favl] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)//求得局部最优解
//x0为初始值，可以使用蒙特卡洛法先找合适的初始值
//option:interior-point,sqp,active-set,trust-region-reflective,可以都使用来求解，体现稳健性
//@fun：要写成一个单独的m文件存储目标函数
//@nonlfun：表示非线性部分的约束，同样也要单独编写一个m文件
//function [c,ceq] = nonlfun(x)
//c = [非线性不等式约束1；...];
//ceq = [非线性等式约束1；...];

最大化最小模型

在最不利的条件下，寻求最有利的策略，如急救中心选址等

[x,fval] = fminimax(@Fun.x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)
//目标函数用一个函数向量表示

蒙特卡洛法（随机取样法）

是一种随机模拟方法，是使用随机数来解决很多计算问题的方法。由大数定律可知，当样本容量足够大时，事件发生的频率可以近似为其发生的概率。是计算机仿真的前期模型。
蒙特卡洛法更多的是一种想法，利用非常多次的随机数来模仿时间的发生，从而近似得到想要的结果，具体的算法根据不同的问题而决定。

应用

三门问题
排队论

图论

最短路径模型

迪杰斯特拉算法：可以用于有向图，但不能处理负权重

[p,d] = shortestpath(G,start,end,[,'Method',algorithm])
//G-输入图
//start 起始的节点，end目标节点
//[,'Method'] 计算最短路径的算法，一般不作具体设置
//P-最短路径经过的节点，d-最短距离

Method中可选的算法

d = distances(G,[,'Method',algorithm]) //返回距离矩阵
[nodeIDs,dist] = nearest(G,s,d,[,'Method',algorithm])
//找给定范围内所有的点，s是指定节点，d为指定距离
//nodeIDs是符合条件的节点，Dist是这些节点与s的距离

智能分析类模型

遗传算法

先po一个看过写的不错的文章
遗传算法
遗传算法在实际上和生物学上的遗传类似，都是通过群体搜索技术，根据适者生存的原则进行逐代进化，最终得到最优解（或准最优解）
主要操作：初始群体的产生、求每一个体的适应度（生物个体对于生存环境的适应程度，越适应那么其得以存活和繁衍的概率就越大）、根据适者生存的原则选择优良个体、被选出的优良个体两两配对，通过随机交叉其染色体的基因并随机变异某些染色体的基因生成下一代群体，按此方法使群体逐代进化，知道满足进化终止条件

实现方法

1. 根据具体问题确定可行解域，确定一种编码方法，能用数值串或字符串表示可行解域的每一解
2. 对每一解应有一个度量好坏的依据，用适应度函数表示，一般由目标函数构成
3. 确定进化参数群体规模M，交叉概率pc，变异概率pm，进化终止条件
   编码长度。编码长度取决于问题解的精度，精度越高，编码越长；
   种群规模。规模小，收敛快但降低了种群的多样性，N=20-200；
   交叉概率。较大的交叉概率容易破坏种群中已形成的优良结构，使搜索具有太大随机性；较小的交叉概率发现新个体的速度太慢，一般取值为P_c=0.4-0.99
   变异概率。变异概率太小，则变异操作产生新个体的能力和抑制早熟现象的能力会较差；变异概率过高随机性过大，一般建议取值范围为0.005～0.01
   终止进化代数。算法运行结束的条件之一，一般取100～1000；也可以选择将精度作为结束条件

生物遗传概念	遗传算法中的作用
适者生存	算法停止时，最优目标值的可行解有最大的可能性被留住（轮盘赌选择法）
个体	可行解
染色体	可行解的编码（一般采用二进制编码）
基因	可行解中每一分量的特征
适应性	适应度函数值
种群	根据适应度函数值选取的一组可行解
交配	通过交配原则产生一组新可行解的过程，它决定了遗传算法的全局搜索能力
变异	编码的某一分量发生变化的过程，它决定了遗传算法的局部搜索能力

推一个十分钟的小视频简单说明遗传算法

蚁群算法

起源：蚂蚁会找一条从巢穴到食物源之间的最短距离，当在这条路上放置一个障碍物后，一段时间后蚂蚁会再次重新走出一条最短距离。这个算法对于解决TSP问题取得了比较好的结果

本质：

• 选择机制：信息素越多的路径，被选择的概率越大。
• 更新机制：路径上面的信息素会随蚂蚁的经过而增长，而且同时也随时间的推移逐渐挥发消失。
• 协调机制：蚂蚁间实际上是通过分泌物来互相通信、协同工作的。

基本原理：
蚂蚁在路径上释放信息素。碰到还没走过的路口，就随机挑选一条路走。同时，释放与路径长度有关的信息素。信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高路径。最优路径上的信息素浓度越来越大。最终蚁群找到最优寻食路径。

算法的结果具有随机性，要多次运算

粒子群算法

这个算法是基于模拟鸟群捕食的行为提出的。它的核心思想是利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的可行解。

基本概念

• 粒子：优化问题的候选解
• 位置：候选解所在位置
• 速度：候选解移动的速度
• 适应度：评价粒子优劣的值，一般设置为目标函数值
• 个体最佳位置：单个粒子迄今为止找到的最佳位置
• 群体最佳位置：所有粒子迄今为止找到的最佳位置

具体算法

核心公式

一般情况下，个体学习因子和社会学习因子取2比较合适，惯性权重取0.9-1.2是比较合适的，一般取0.9即可


较大的惯性权重有利于进行全局搜索，而一个较小的权值则更有利于局部搜索。

模型拓展

1. 为了平衡全局搜索和局部搜索的能力，提出来线性递减惯性权重
   
2. 非线性递减惯性权重
   
3. 自适应惯性权重
   
   适应度越小，说明距离最优解越近，此时更需要局部搜索。
   最大值则相反
4. 随机惯性权重，可以避免在迭代前期局部搜索能力的不足；也可以避免在迭代后期全局搜索能力的不足。
   
5. 压缩（收缩）因子法
   个体学习因子和社会学习因子决定了粒子本身经验信息和其他粒子的经验信息对粒子运行轨迹的影响，反映了粒子群之间的信息交流。当C1的值较大，会使粒子过多的在自身全部范围内搜索，而C2值较大时，会使粒子过早收缩到局部最优值。
   
6. 非对称学习因子
   令C1线性递减，C2线性递增，从而加强了粒子向全局最优点的收敛能力
   
7. 自动退出迭代循环
   当粒子已经找到最佳位置后，再增加迭代次数就是浪费计算时间，因此我们可以设计一个策略，当到达一定条件后自动退出迭代。
   

matlab自带粒子群函数

particleswarm函数采用的是自适应的邻域模式

[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
% Obj_fun是单独存储的自适应函数，即目标函数
% narvs是自变量个数
% x_lb，x_ub分别是下界和上界

邻域模式：粒子群在搜索过程中只将其周围部分粒子视为邻域粒子，这种模式使得粒子群可以被分割成多个不同的子群体，有利于在多个区域进行搜索。
全局模式：是邻域模式的极端情况，它将所有其他粒子都视为领域粒子，这种模式具有较快的收敛速度，但容易陷入局部最优。
自适应体现在：如果适应度开始停滞，粒子群搜索会从邻域模式向全局模式转化，一旦适应度开始下降，则恢复为邻域模式，以免陷入局部最优。当适应度的停滞次数足够大时，惯性系数开始逐渐变小，从而利于局部搜索。
option中可以修改的参数

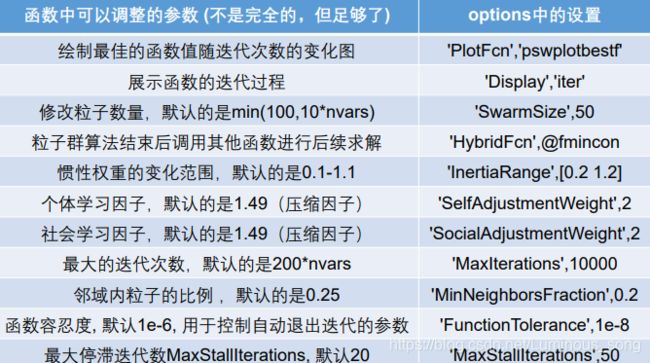
options = optimoptions('particleswarm','PlotFcn','pswplotbestf') 

粒子群算法进阶应用

求解方程组

1. vpasolve函数
2. fsolve函数
3. 粒子群算法
   利用最小二乘的思想
   找一组解使得目标函数尽量小，即可得到最优解

多元函数拟合

粒子群算法主要用于三元及以上函数的拟合

[k,fval] = lsqcurvefit(@fit_fun,k0,x,y,lb,ub)
//非线性最小二乘拟合函数

拟合微分方程

如果微分方程或微分方程组有解析解（dsolve可解），则转化为函数拟合问题。这个主要讨论ode45求出数值解的情况。
将残差平方和作为适应度函数，解出残差平方和最小时的参数数值。

模拟退火算法

参考资料：数学建模清风第二次直播：模拟退火算法

爬山法

1. 在解空间中随机生成一个初始解
2. 根据初始解的位置，我们在下一步有两种走法：向左邻域或向右邻域走一步（步长越小越好）
3. 比较不同走法下目标函数的大小，决定下一步往哪个方向走，如果向左目标函数比较大，就向左走（求最大值）
4. 不断重复这个过程，直到找到一个极大值点，则结束搜索
   这个方法容易陷入局部最优

从优化角度看模拟退火

温度一定时，△f越小，概率越大，即目标函数相差越小接受的可能性越大
△f一定时，温度越高，概率越大，即搜索前期温度较高时更有可能接受新解

预测模型

微分方程模型

无法直接找到原始数据之间的关系，但可以找到原始数据变化速度之间的关系，通过公式推导转化为原始数据之间的关系。
常用模型：传染病模型、人口模型（Malthus模型和Logistic模型）
适用场景：疾病的传播预测、人口数量或城市发展水平预测等

解

解析解：给出解的具体表达式

[x,y] = dsolve('y-Dy = 2*x','x')
% dsolve('方程1'，'方程2',....,'方程n','初始条件'，‘自变量’)

数值解：对求解区间进行剖分，然后把微分方程离散成在节点上的近似公式或近似方程，最后结合定解条件求出近似解

[x,y] = ode45('df1',[0,1],3) % 解决非刚性问题
% df1为具体的微分方程（组），写成单独的m文件
% ode45('微分方程m文件名'，‘自变量范围’，‘初始值’)
% ode15s 解决刚性问题

微分方程模型

1. 人口预测模型（Malthus模型）
   假定人口的增长率r为常数
   
2. 阻滞增长模型（Logistic模型）
   假设人口增长率为随人口数量变化的线性函数
   r(x) = r-sx x = xm时，r(xm) = 0 -> s = r/xm
   
3. 捕食者-猎物模型（Lotka-Volterra模型）
   食饵的增长
   
   捕食者的死亡
   
   在考虑人工捕获时，假设e表示捕获能力
   
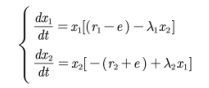
4. 种群相互竞争模型
   我们在阻滞增长模型的基础上进行建模
   
   由于甲乙两种群的食物相同，所以对对方的增长会造成影响
   
   其中σ1表示单位数量的乙种群消耗的供养甲的食物量为单位数量甲种群的σ1倍，如果σ1<1则乙的竞争力弱于甲
   一般情况下σ1和σ2是相互独立的，若甲乙两种群食物完全一样则σ1σ2 = 1
5. 种群相互依存模型
   
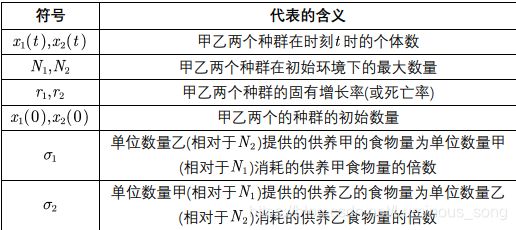
   相互依存分为三种情况：甲乙均可以单独生存、甲乙均不可以单独生存、甲可以单独生存而乙不可以（或反过来）
   情况一：甲可以单独生存而乙不可以
   
   
   情况二：甲乙均可以单独生存
   
   情况三：甲乙均不能独自生存，在这种情况下甲乙均会灭亡
   
6. 传染性模型

• 符号系统：易感者（S）、潜伏者（E）、感染者（I）、康复者（R）
• SI模型：
  
• SIS模型
  
  
• SIR模型
  
• SIRS模型：N =S+ I + R
  
• SEIR模型：潜伏者E不具有传染性
  

回归分析预测

在分析自变量和因变量之间相关关系的基础上，建立变量之间的回归方程，并将回归方程作为预测模型
适用场景：样本数量较少，自变量与因变量间的变化具有明显的逻辑关系，处理横截面数据（同一时间不同对象的数据）
主要有三个使命：识别重要变量、判断相关性的方向、确定权重（回归系数）

线性、非线性回归与拟合

一元线性回归

Logistic回归&Probit回归

因变量是分类变量

向量自回归（E、F题）

Pearson相关

Spearman等级相关系数

标准化回归

一个因变量对多个自变量之间的关系

偏最小二乘回归

多个变量和多个变量之间的关系

马尔科夫预测

对事件的全面预测，不仅要能够指出事件发生的各种可能结果，而且还必须给出每一种结果出现的可能性，说明被预测的视角在预测期内出现每一种结果的可能性程度。未来状态只和现在的状态有关
使用场景：市场占有率的预测和销售期望利润的预测以及其他商业领域的预测等。在各个期间或者状态是，变量面临的下一个期间或状态的转移概率都是一样的、不随时间变化的。

步骤

1、根据历史的数据推算出各类人员的转移概率，利用转移概率来计算出转移矩阵；
2、统计初始时刻点的各类人员的分布状况；
3、建立马尔科夫模型，预测未来各类人员的状况

神经网络预测

用非线性关系来预测问题
适合多指标预测
常用方法：利用前i年的数据预测第i+1年的数据

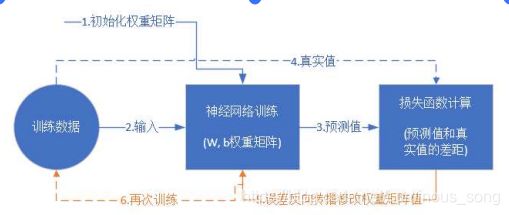
BP神经网络预测

• 训练集：用于模型拟合的数据样本
• 验证集：是模型训练过程中单独留出的样本集，主要用于调整模型的超参数和对模型的能力进行初步评估
• 测试集：用来评估最终模型的泛化能力
  一般先在matlab中导入数据，然后使用神经网络拟合工具箱

在训练过多数要考虑过拟合现象

时间序列预测

基本概念

同一对象按时间顺序排列的，随时间变化且相互关联的数据序列，是一种定理分析方法

常用模型：移动平均法、指数平滑法、自回归AR，移动平均MA，ARIMA模型等

适用场景：国民经济市场潜量预测，气象预测、生态平衡等等，数据量较大

时间序列分解

数值变化规律包括：

• 长期变动趋势（T）
  统计指标在相当长的一段时间内，收到长期趋势因素的影响，表现出持续上升或持续下降的趋势
• 季节趋势（S）
  由于季节的转变使得指标数值发生周期性变动，这里的季节可以是月、季、周为时间单位，不能以年为时间单位
• 循环变动（C）
  与季节变动不同，通常以若干年为周期，这种周期变动的特征是增加和减少交替出现，而不是严格规定的周期性连续变动
• 不规则变动（I）
  是某些随机因素导致的数值变化，这些因素不可预知而且没有规律可言（在回归中被称为扰动项）
  这些变动可能会同时出现在一个时间序列里面，这四种变动与指标数值的关系可能是叠加也可能是叠乘
• 注意

1. 数据具有年内的周期性时才能使用时间序列分解
2. 在具体的时间序列图上，如果随着时间的推移，序列的季节波动越来越大，则反映各种变动之间的关系发生变化，建议使用乘积模型，反之，使用叠加模型。如果不存在季节波动，则两种分解均可

几种模型

指数平滑模型

分为季节性和非季节性模型，季节性模型只有在为活动数据集定义周期数才可用

1. Simple模型
   使用条件：不含趋势和季节成分
   
   α为平滑系数，如果时间序列具有不规则的起伏变化，但长期趋势接近一个稳定常数，α一般较小；如果有迅速变化的倾向，α取较大值；如果变化缓慢，取较小的值
   只能预测一期
2. Holt线性趋势模型
   使用条件：线性趋势，不含季节成分
   
3. 阻尼趋势模型
   使用条件：线性趋势逐渐减弱且不含季节成分
   是在Holt模型的基础上缓解较高的线性趋势
   
4. 简单季节性
   使用条件：含有稳定的季节成分、不含趋势
   
5. 温特加法模型
   使用条件：含有线性趋势和稳定的季节成分
   
6. 温特乘法模型
   使用条件：含有线性趋势和不稳定的季节成分
   

AR§模型

也称为自回归模型，所谓自回归就是将自己的1至p阶滞后项视为自变量来进行回归，AR§模型一定是平稳的时间序列模型

只能用于预测与自身前期相关的经济现象，即受自身历史因素影响较大的经济线性

平稳序列

MA(q)模型

称为q阶移动平均模型

ARMA(p,q)模型

自回归移动平均模型

ACF自相关系数

使用前提，数据为平稳序列。

PACF偏自相关函数

反映的是两个自变量之间的之间线性相关程度

ARIMA(p,d,q)模型

称为差分自回归移动平均模型

SARIMA模型

步骤

1. SPSS处理时间序列中的缺失值，如果缺失值在开头或尾部可以直接删除，如果在中间使用SPSS中转换->替换缺失值->选择替换方法
   
2. 定义时间变量
3. 画出时间序列图，并对数据进行分析，看波动性和周期性来决定下一步操作和使用的模型
4. （如果由季节变动）进行季节性分解，如果周期是奇数在移动平均值选择所有点相等，并对结果进行说明
   
   如果是乘法模型，乘法季节因子的积为1，是全年的倍数
5. 画出分解后的时序图
6. 建立时间序列分析模型，使用SPSS自带的专家建模器

模糊预测

灰色预测（谨慎使用）

使用场景

使用背景：数据量较少，数据发展呈指数，数据分布位置
通过少量的、不完全的信息，建立数学模型并作出预测
适用场景：小样本情况下的发展预测问题

基本思想

灰色预测对原始数据进行生成处理来寻找系统变动的规律，并生成有较强规律性的数据序列，建立相应的微分方程，从而预测事物未来发展趋势情况

GM(1,1)

是使用原始的离散非负数据列，通过一次累加生成削弱随机性的较有规律的新的离散数据列，然后通过建立一阶微分方程模型，得到在离散点处的解经过累减生成的原始数据的近似估计值，从而预测原始数据的后续发展。

理论基础

数据具有准指数规律。

准指数规律

• 定义级比
  
  定义光滑比
  
  如果任意的级比都落在一个区间长度小0.5的区间内，则数据具有准指数规律，我们可以间接用光滑比来判断，随着k的增加，光滑比会逐渐接近0，我们只要计算出光滑比在（0,0.5）的占比即可，占比越高越好（重点关注后面的期数）

基本原理

1-AGO：对原始数据经过一次累加后的数据列
1-AGO的紧邻均值生成数列：z⁽¹⁾(m) = σx⁽¹⁾(m)+(1-σ)x⁽¹⁾(m-1)(m=2,3,…n) σ = 0.5
GM(1,1)模型的基本形式（灰色微分方程）：x⁽⁰⁾(k) + az⁽¹⁾(k) = b
b为灰作用量，-a表示发展系数，可以将x⁽⁰⁾看做因变量，z⁽¹⁾看做自变量
OLS（普通最小二乘法）：令所有观测值到回归直线的平方和最小
白化方程：dx⁽¹⁾(t)/dt = -ax⁽¹⁾(t) + b

评价

1. 残差检验：

• 相对残差
• 平均相对残差
  
  当平均相对残差小于20%，则认为GM(1,1)对原数据的拟合达到一般要求
  如果平均相对残差小于10%，则认为GM(1,1)对原数据的拟合效果非常好

2. 级比偏差检验
   
   再根据预测出来的发展系数计算出相应的级比偏差和平均级比偏差
   
   平均级比偏差小于0.2，则认为GM(1,1)对原数据的拟合达到一般要求；小于0.1，则认为对原数据的拟合非常好

拓展

• 新信息模型：设x⁽⁰⁾(n+1)为最新信息，将x⁽⁰⁾(n+1)置入X⁽⁰⁾，将新的模型称为新信息GM(1,1)
• 新陈代谢模型：再置入最新信息的同时，去掉最高的信息。这个模型是目前最理想的

聚类模型

K-means聚类

适用场景

与地理位置有关的分类情形，如地物类别划分、村落划分、语言分布位置划分等

算法流程

1. 指定需要划分的簇的个数（类的个数）
2. 随机地选择K个数据对象作为初始的聚类中心（不一定是样本点）
3. 计算其余的各个数据对象到这K个初始聚类中心的距离，把数据对象划分到距离它最近的那个中心所在的簇类中
4. 调整新类并且重新计算出新类的中心
5. 循环步骤三和四，看中心是否不变，如果不变或达到迭代次数则停止循环
6. 结束
   
   注意：在使用时数据的量纲要相同

K-means++算法

此算法只对K-means算法中选取初始聚类中心进行了优化
基本原则是：初始的聚类中心之间的相互距离要尽可能的远

步骤

1. 随机选择一个样本点作为第一个聚类中心
2. 计算每个样本与当前已有聚类中心的最短聚类，这个值越大，表示被选取作为聚类中心的概率越大；最后用轮盘法（根据概率大小来抽签）选出下一个聚类中心
3. 重复步骤二，直到选出K个聚类中心，然后就继续使用标准的K-means算法

层次聚类

也叫系统聚类法，是根据个体检距离将个体向上两两聚类，再将聚合的小群体两两聚合一直到聚为一个整体。计算所有个体之间的距离，最相近距离的个体合体，不断合体。

适用场景

行政区域的划分或分级处理等，如根据城市经济指标划分城市发展等级、根据各类综合指标进行文明城市建设评选等

算法流程

1. 将每个对象看做一类，计算两两之间的最小距离
2. 将距离最小的两个类合并成一个新类
3. 重新计算新类与所有类之间的聚类
4. 重复步骤二和三，直到所有类最后合并成一类
5. 生成聚类谱系图（树状图），结束

用图形估计聚类的数量

肘部法则：通过图形大致的估计出最优的聚类数量
各个类畸变程度之和：各个类的畸变程度等于该类重心与其内部成员位置距离的平方和


J为聚合系数
在excel中画出聚类系数折线图，取趋势最剧烈的类数

密度聚类（DBSCAN）

基本思想

聚类前不需要预先指定聚类的个数，生成的簇的个数与数据相关。
“谁和我挨得近，我就是谁的兄弟，兄弟的兄弟，也是我的兄弟”

基本概念

核心点：在规定的半径内有不少于MinPts数目的点
边界点：在半径内点的数量小于MinPts，但落在核心点的领域内
噪音点：即不是核心点也不是边界点

模糊聚类

基于目标函数的模糊聚类算法：该方法把聚类分析归结成一个带约束的非线性规划问题，通过优化求解获得数据集的最优模糊划分和聚类
没咋学会
po个博文

步骤

1. 获取原始数据
2. 数据标准化处理
   
3. 建立模糊相似矩阵
4. 聚类

神经网络聚类

采用竞争学习算法来指导网络的聚类过程，主要是无监督的学习

SOM神经网络模型

BP神经网络具有输入层、隐含层(一层或多层)和输出层，通过这三层的神经网络可以逼近任意非线性函数

适用场景

样本数量较多时的分类问题

基本思想

SOM神经网络[11]是由芬兰神经网络专家Kohonen教授提出的，该算法假设在输入对象中存在一些拓扑结构或顺序，可以实现从输入空间(n维)到输出平面(2维)的降维映射，其映射具有拓扑特征保持性质,与实际的大脑处理有很强的理论联系。
　SOM网络包含输入层和输出层。输入层对应一个高维的输入向量，输出层由一系列组织在2维网格上的有序节点构成，输入节点与输出节点通过权重向量连接。 学习过程中，找到与之距离最短的输出层单元，即获胜单元，对其更新。同时，将邻近区域的权值更新，使输出节点保持输入向量的拓扑特征。

算法流程

1. 网络初始化，对输出层每个节点权重赋初值；
2. 将输入样本中随机选取输入向量，找到与输入向量距离最小的权重向量；
3. 定义获胜单元，在获胜单元的邻近区域调整权重使其向输入向量靠拢；
4. 提供新样本、进行训练；
5. 收缩邻域半径、减小学习率、重复，直到小于允许值，输出聚类结果。

python代码实现

还没有完全懂先po个代码

import numpy as np
import pylab as pl
 
class SOM(object):
    def __init__(self, X, output, iteration, batch_size):
        """
        :param X:  形状是N*D， 输入样本有N个,每个D维
        :param output: (n,m)一个元组，为输出层的形状是一个n*m的二维矩阵
        :param iteration:迭代次数
        :param batch_size:每次迭代时的样本数量
        初始化一个权值矩阵，形状为D*(n*m)，即有n*m权值向量，每个D维
        """
        self.X = X
        self.output = output
        self.iteration = iteration
        self.batch_size = batch_size
        self.W = np.random.rand(X.shape[1], output[0] * output[1])
        print (self.W.shape)
 
    def GetN(self, t):
        """
        :param t:时间t, 这里用迭代次数来表示时间
        :return: 返回一个整数，表示拓扑距离，时间越大，拓扑邻域越小
        """
        a = min(self.output)
        return int(a-float(a)*t/self.iteration)
 
    def Geteta(self, t, n):
        """
        :param t: 时间t, 这里用迭代次数来表示时间
        :param n: 拓扑距离
        :return: 返回学习率，
        """
        return np.power(np.e, -n)/(t+2)
 
    def updata_W(self, X, t, winner):
        N = self.GetN(t)
        for x, i in enumerate(winner):
            to_update = self.getneighbor(i[0], N)
            for j in range(N+1):
                e = self.Geteta(t, j)
                for w in to_update[j]:
                    self.W[:, w] = np.add(self.W[:,w], e*(X[x,:] - self.W[:,w]))
 
    def getneighbor(self, index, N):
        """
        :param index:获胜神经元的下标
        :param N: 邻域半径
        :return ans: 返回一个集合列表，分别是不同邻域半径内需要更新的神经元坐标
        """
        a, b = self.output
        length = a*b
        def distence(index1, index2):
            i1_a, i1_b = index1 // a, index1 % b
            i2_a, i2_b = index2 // a, index2 % b
            return np.abs(i1_a - i2_a), np.abs(i1_b - i2_b)
 
        ans = [set() for i in range(N+1)]
        for i in range(length):
            dist_a, dist_b = distence(i, index)
            if dist_a <= N and dist_b <= N: ans[max(dist_a, dist_b)].add(i)
        return ans
 
 
    def train(self):
        """
        train_Y:训练样本与形状为batch_size*(n*m)
        winner:一个一维向量，batch_size个获胜神经元的下标
        :return:返回值是调整后的W
        """
        count = 0
        while self.iteration > count:
            train_X = self.X[np.random.choice(self.X.shape[0], self.batch_size)]
            normal_W(self.W)
            normal_X(train_X)
            train_Y = train_X.dot(self.W)
            winner = np.argmax(train_Y, axis=1).tolist()
            self.updata_W(train_X, count, winner)
            count += 1
        return self.W
 
    def train_result(self):
        normal_X(self.X)
        train_Y = self.X.dot(self.W)
        winner = np.argmax(train_Y, axis=1).tolist()
        print (winner)
        return winner
 
def normal_X(X):
    """
    :param X:二维矩阵，N*D，N个D维的数据
    :return: 将X归一化的结果
    """
    N, D = X.shape
    for i in range(N):
        temp = np.sum(np.multiply(X[i], X[i]))
        X[i] /= np.sqrt(temp)
    return X
def normal_W(W):
    """
    :param W:二维矩阵，D*(n*m)，D个n*m维的数据
    :return: 将W归一化的结果
    """
    for i in range(W.shape[1]):
        temp = np.sum(np.multiply(W[:,i], W[:,i]))
        W[:, i] /= np.sqrt(temp)
    return W
 
#画图
def draw(C):
    colValue = ['r', 'y', 'g', 'b', 'c', 'k', 'm']
    for i in range(len(C)):
        coo_X = []    #x坐标列表
        coo_Y = []    #y坐标列表
        for j in range(len(C[i])):
            coo_X.append(C[i][j][0])
            coo_Y.append(C[i][j][1])
        pl.scatter(coo_X, coo_Y, marker='x', color=colValue[i%len(colValue)], label=i)
 
    pl.legend(loc='upper right')
    pl.show()
 
#数据集：每三个是一组分别是西瓜的编号，密度，含糖量
data = """
1,0.697,0.46,2,0.774,0.376,3,0.634,0.264,4,0.608,0.318,5,0.556,0.215,
6,0.403,0.237,7,0.481,0.149,8,0.437,0.211,9,0.666,0.091,10,0.243,0.267,
11,0.245,0.057,12,0.343,0.099,13,0.639,0.161,14,0.657,0.198,15,0.36,0.37,
16,0.593,0.042,17,0.719,0.103,18,0.359,0.188,19,0.339,0.241,20,0.282,0.257,
21,0.748,0.232,22,0.714,0.346,23,0.483,0.312,24,0.478,0.437,25,0.525,0.369,
26,0.751,0.489,27,0.532,0.472,28,0.473,0.376,29,0.725,0.445,30,0.446,0.459"""
 
a = data.split(',')
dataset = np.mat([[float(a[i]), float(a[i+1])] for i in range(1, len(a)-1, 3)])
dataset_old = dataset.copy()
 
som = SOM(dataset, (5, 5), 1, 30)
som.train()
res = som.train_result()
classify = {
     }
for i, win in enumerate(res):
    if not classify.get(win[0]):
        classify.setdefault(win[0], [i])
    else:
        classify[win[0]].append(i)
C = []#未归一化的数据分类结果
D = []#归一化的数据分类结果
for i in classify.values():
    C.append(dataset_old[i].tolist())
    D.append(dataset[i].tolist())
draw(C)
draw(D)

来源
还可以使用matlab中的nctool工具箱

贝叶斯判别

是找到一个错判平均损失最小的判别准则

基本概念

1. 错判损失：指的是将属于某类的实体错判为其他类，在实际生活中会导致的损失。
   使用判别法D将第i类的样本错判为第j类，错判损失记作L ( j ∣ i ; D ) =L(j|i;D)=L(j∣i)

基本思路

直接为每个类别产生一个判别函数式。如果原始个案被分为K类，则直接产生K个函数式。对于待判定类别的个案，直接把该个案各属性的取值代入到每个判别函数式中，那个函数式的值最大，该个案就被划归到那个类别中。
一般用spss进行

支持向量机

SVM 即支持向量机（Support Vector Machine）， 是有监督学习算法的一种，用于解决数据挖掘或模式 识别领域中数据分类问题。
它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。由简至繁的模型包括：

• 当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机
• 当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机
• 当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机

代码实现

clc;
clear;
N=10;
%下面的数据是我们实际项目中的训练样例（样例中有8个属性）
correctData=[0,0.2,0.8,0,0,0,2,2];
errorData_ReversePharse=[1,0.8,0.2,1,0,0,2,2];
errorData_CountLoss=[0.2,0.4,0.6,0.2,0,0,1,1];
errorData_X=[0.5,0.5,0.5,1,1,0,0,0];
errorData_Lower=[0.2,0,1,0.2,0,0,0,0];
errorData_Local_X=[0.2,0.2,0.8,0.4,0.4,0,0,0];
errorData_Z=[0.53,0.55,0.45,1,0,1,0,0];
errorData_High=[0.8,1,0,0.8,0,0,0,0];
errorData_CountBefore=[0.4,0.2,0.8,0.4,0,0,2,2];
errorData_Local_X1=[0.3,0.3,0.7,0.4,0.2,0,1,0];
 sampleData=[correctData;errorData_ReversePharse;errorData_CountLoss;errorData_X;errorData_Lower;errorData_Local_X;errorData_Z;errorData_High;errorData_CountBefore;errorData_Local_X1];%训练样例

type1=1;%正确的波形的类别，即我们的第一组波形是正确的波形，类别号用 1 表示
type2=-ones(1,N-2);%不正确的波形的类别，即第2~10组波形都是有故障的波形，类别号用-1表示
groups=[type1 ,type2]';%训练所需的类别号
j=1;
%由于没有测试数据，因此我将错误的波形数据轮流从训练样例中取出作为测试样例
for i=2:10
   tempData=sampleData;
   tempData(i,:)=[];
    svmStruct = svmtrain(tempData,groups);
    species(j) = svmclassify(svmStruct,sampleData(i,:));
    j=j+1;
end
species

评价模型

模糊综合评价模型

把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价
适用场景：无具体的评价标准，通过统计问卷等形式进行的评价问题

基本原理

模糊综合评价的指标都是模糊性的，例如帅、高、白等
所以利用隶属函数来判断隶属度
三种表示方法：

1. Zadeh（扎德表示法）
   
2. 序偶表示法
   
3. 向量表示法
   
   集合分类：
   偏小型（年轻，小）、中间型（中年，暖）、偏大型（年老，大，热）
   

隶属函数的确定方法

1. 模糊统计法：找多个人对同一个模糊概念进行描述，用隶属频率去定义隶属度
2. 借助已有的客观尺度：一般使用经常使用的公式来定义
3. 指派法：根据问题的性质直接套用某些分布作为隶属函数
   

应用

1. 确定有三个集合：因素集（评价指标集）、评语集（评价的结果）、权重集（指标的权重），确定权重的方法有无数据：层次分析法，有数据：熵权法

2. 确定模糊综合判断矩阵
   

3. 综合评判：B = A · R
   

层次分析法（AHP）

将于决策总是有关的元素分解成目标、准则、方案等层次，通过两两比较的形式来进行综合评价，擅长于求权重
适用场景：表叫适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题，常用于计算指标的权重（和模糊综合评价共同使用）
要选好指标，确定权重表格，权重表格中的数据均按此表格填写判断矩阵

一致矩阵：各行（各列）之间成比例
一致性检验：在使用判断矩阵求权重之前，要先进行一致性检验，是检验判断矩阵与一致检验是否有太大区别

使用判断矩阵求权重：

1. 算术平均法求权重
   
2. 几何平均法求权重
   
3. 特征值法求权重
   

Topsis综合评价模型

根据有限个评价对象与理想化目标的接近程度进行排序的方法，是在现有的对象中进行相对优劣的评价，是多目标决策分析中一种常用的有效方法
适用场景：无具体的评价指标，大体系的综合评价，要有理想化指标数据，如环境质量评价、医疗质量综合评价等
步骤：

1. 将原始矩阵正向化
   
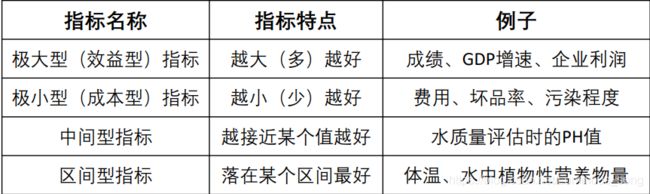
   所谓正向化就是将各种类型的指标都统一为极大型
   极小型——》极大型：max-x
   中间型——》极大型：
   
   区间型——》极大型：
   
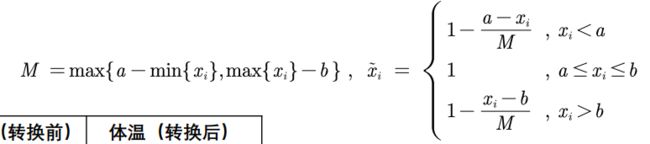
2. 正向化矩阵标准化：每一个元素/所在列各元素平方和开根
3. 计算得分并归一化
   

熵权法

是一种客观地赋权方法，利用数据本身来决定权重。指标的变异程度（波动程度）越小，所反映的信息量就越小，所占的权重也应该越小。

信息量

越有可能发生的事情，所含的信息量越小；越不可能发生的事情，所含的信息量就越大。这个可能性用概率来表示。
信息量用I(x)来表示 I(x) = -ln(p(x))
信息熵H(x)

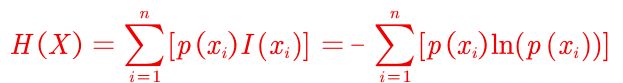
从这个公式可以看出来，信息熵是对信息量的期望，所以信息量越大，我们所能期望得到的信息量就越少，相应的权重就小。

步骤

1. 判断输入的矩阵是否存在负数，如果存在要重新标准化到非负区间
   一般是在Topsis得到的正向化，标准化后的矩阵上进行判断。重新标椎化的公式为：
   
2. 计算第j项指标下第i个样本所占的比重，并将其看做相对熵计算中用到的概率，得到概率矩阵P
   
3. 计算每个指标的信息熵，并计算信息效用值，并归一化得到每个指标的熵权
   
   信息效用值：dj = 1 - ej
   

我们也可以用指标的标准差来衡量变异程度，指标的标准差越大，信息熵越小

[n,m] = size(Z);
    D = zeros(1,m);  % 初始化保存信息效用值的行向量
    for i = 1:m
        x = Z(:,i);  % 取出第i列的指标
        p = x / sum(x);
        % 注意，p有可能为0，此时计算ln(p)*p时，Matlab会返回NaN，所以这里我们自己定义一个函数
        e = -sum(p .* mylog(p)) / log(n); % 计算信息熵
        D(i) = 1- e; % 计算信息效用值
    end
    W = D ./ sum(D);  % 将信息效用值归一化，得到权重 

主成分分析&因子分析

研究一堆自变量之间的重要性
由于在前面已经讲过了主成分分析，所以这一部分主要讲因子分析

因子分析

因子分析法通过研究变量间的相关系数矩阵，把这些变量间错综复杂的关系归结成少数几个综合隐私，这种方法比主成分分析更容易解释

因子分析需要构造一个因子模型，并伴随几个关键性的假定，可以有许多解

原理

满足的条件

数据包络分析模型（DEA）

根据多项投入指标和多项产出指标，利用线性规划的方法，对具有可比性的同类型单位进行相对有效性评价的一种数量分析方法
适用场景：评价效率的问题

基本思想

DEA以决策单位各输入/输出的权重为变量，从最有利于决策单元的角度进行评价，从而避免了确定各指标在优先意义下的权重；
假定每个输入都关联到一个或者多个输出，而且输入/输出之间确实存在某种关系，使用DEA方法则不必确定这种关系的显示表达式。

基本原理

数据包络分析是评价多输入指标和多输出指标的较为有效的方法，将投入与产出进行比较。它的结果包含的意思有：

①θ=1，DEA有效，表示投入与产出比达到最优

②θ<1，非DEA有效，表示投入与产出比没有达到最优，一般来说，θ越大说明效果越好。

数据包络分析是通过对投入的指标和产出的指标做了一个线性规划，并且进行变换后，然后根据其线性规划的对偶问题（线性规划对偶问题具有经济学意义），求解这个对偶问题的最值就是θ。

公式表示

一篇博文解释很清楚

代码实现

clc,clear
 
format long
 
load('data.txt');%把原始数据保存在纯文本文件data.txt中
 
X=data(:,[1:3]);%X为输入变量，3为输入变量的个数
 
X=X';
 
Y=data(:,[4:5]);%Y为输出变量，5（3+2），2为输出变量的个数
 
Y=Y';
n=size(X',1);m=size(X,1);s=size(Y,1);
 
A=[-X' Y'];
 
b=zeros(n,1);
 
LB=zeros(m+s,1);UB=[];
 
for i=1:n
   
    f=[zeros(1,m) -Y(:,i)'];
 
   Aeq=[X(:,i)',zeros(1,s)];beq=1;
 
   w(:,i)=linprog(f,A,b,Aeq,beq,LB,UB);
 
   E(i,i)=Y(:,i)'*w(m+1:m+s,i);
 
end
 
theta=diag(E)';
 
fprintf('用DEA方法对此的相对评价结果为：\n');
 
disp(theta);
 
omega=w(1:m,:)
 
mu=w(m+1:m+s,:)

灰色关联分析

应用范围

当样本个数比较大的时候用标准化回归，当样本数比较小时，才用灰色关联分析。
可以进行系统分析和综合评价

基本思想

根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的关联度越大，反之越小。

基本过程

1. 要选取能够反映系统行为特征的数据序列，称为找系统行为的映射量，用映射量来间接地表征系统行为。例如用国民平均接受教育的年数来反映教育发达程度。
2. 做出各个数据序列的图像，从直观上进行分析，在论文中要对图形中的各条曲线进行说明
3. 确定分析数列
   母序列：能反应系统行为特征的数据序列，类似于因变量Y，这里记为X0
   子序列：影响系统行为的因素组成的数据序列，类似于自变量X，记为（X1，X2，…，Xm）
4. 对变量进行预处理：去量纲，缩小变量范围便于计算，先正向化
   先求出每个指标的均值，再用该指标中的每个元素除以均值
5. 计算子序列中这个指标与母序列的关联系数
   
   
6. 计算灰色关联度
   
   当母序列有多个时，分别计算每个母序列与子序列的灰色关联度
   在进行综合评价时，要计算各个指标的权重，用各个指标的灰色关联度除以所有灰色关联度的和，每个评价对象的得分为标准化后的矩阵乘以各个指标的权重，再进行归一化即可

关联、因果与比较

格兰杰因果检验&协整检验

结构方程模型