Unity基础（四）--3D数学
文章目录
- 一、向量
-
- 基本属性
- 向量与标量的乘除
- 二、三角函数
-
- 角的度量方式
- 三角函数
- 点乘（Dot）
- 叉乘
- 三、欧拉角与四元数
-
- 欧拉角
- 四元数
-
- 基本运算
-
- 1、与向量相乘
- 2、与四元数相乘
- 四、三维向量API
-
- Vector3
- 四元数
-
- 练习
- 五、坐标系
-
- 坐标系转换
以下是本篇文章正文内容，下面案例可供参考
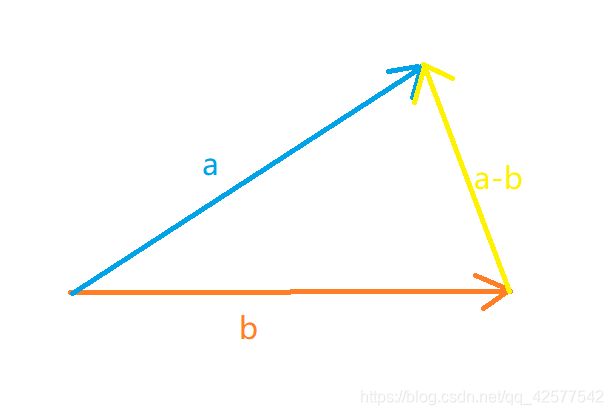
一、向量
一个数字列表，表示各个维度上有位移
基本属性
- 有大小方向的物理量
1、大小就是向量的模长
float dis=vector.magnitude;
2、方向描述空间中向量的指向
vector1.Normalize()；将vector1自身设置为单位向量 - 可以表示物体的位置
- 物体坐标向量，从世界（0，0，0）出发指向物体的一条线段
//求向量模长
private void Demo01()
{
Vector3 pos = this.transform.position;
//数学公式
float m01 = Mathf.Sqrt(Mathf.Pow(pos.x, 2) + Mathf.Pow(pos.y, 2) + Mathf.Pow(pos.z, 2));
//API：获取向量模长
float m02 = pos.magnitude;
//两点间距离
float m03 = Vector3.Distance(Vector3.zero, pos);
Debug.LogFormat("{0}--{1}--{2}", m01, m02, m03);
}
//获取向量方向也称“标准化向量”，“归一化向量”，即获取该向量的单位向量
private void Demo02()
{
Vector3 pos = this.transform.position;
Vector3 n01 = pos / pos.magnitude;
//API:获取向量的方向 标准化 归一化
Vector3 n02 = pos.normalized;
}
- 向量相减
(x1,y1,z1)-(x2,y2,z2)=((x1-x2),(y1-y2),(z1-z2))
private void Demo03()
{
//向量计算
Vector3 relativeDirction = t1.position - t2.position;
//方向：指向被减向量
//大小：两点间距
//t3沿着relativeDirction移动
//如果relativeDirction不标准化，t3的移动的距离会根据t1与t2之间的距离变化而改变
t3.Translate(relativeDirction.normalized);
t3.position = t3.position + relativeDirction.normalized;
}
向量与标量的乘除
- 乘法：k*（x，y，z）=（xk，yk，z*k）；
- 除法：（x，y，z）/k=（x/k，y/k，z/k）
- 几何意义：缩放向量长度
二、三角函数
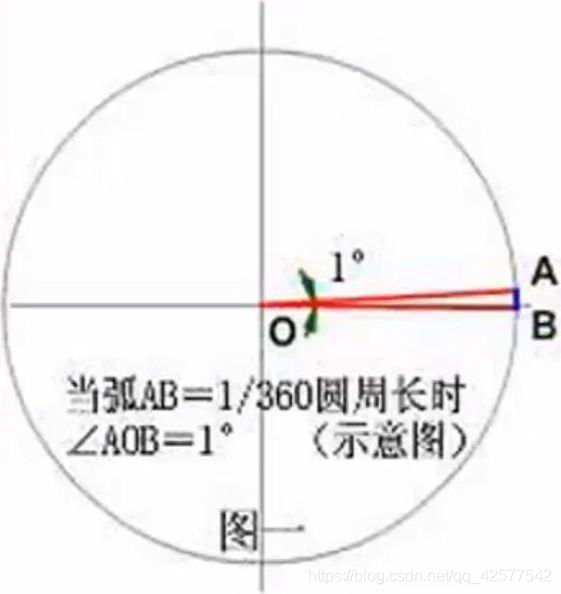
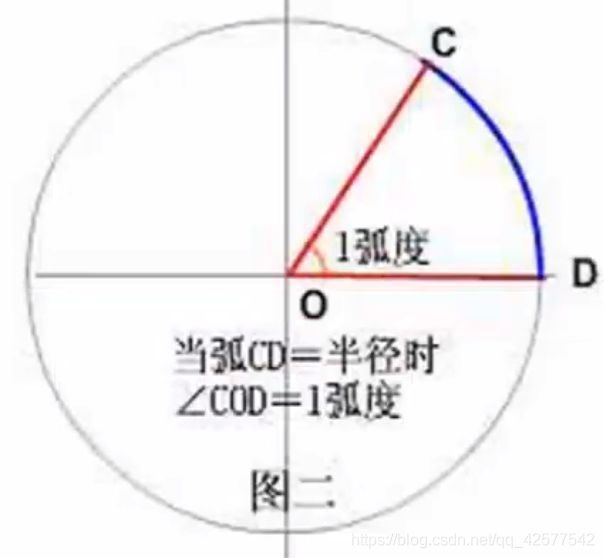
角的度量方式
-
角度Degree
当弧长等于圆周长的360分之一时，夹角为1度
-
弧度Radian
弧长等于半径时，夹角为1弧度
-
角度与弧度的换算；
PI=180度
1弧度=180度/PI
1角度=PI/180度
代码如下（示例）：
private void Demo04()
{
float d1=60;
//角度->弧度
float r1 = d1 * Mathf.PI / 180;
float r2 = d1 * Mathf.Deg2Rad;
//Mathf.Rad2Deg
}
三角函数
知道一个边和一个角用三角函数；知道两条边用反三角函数
API
注：radian为弧度（Mathf.Deg2Rad）
- Mathf.Sin(float radian)
- Mathf.Cos(float radian)
- Mathf.Tan(float radian)
- Mathf.Asin(float radian)
- Mathf.Acos(float radian)
- Mathf.Atan(float radian)
点乘（Dot）
又称“点积”或“内积”
- 几何意义：a*b=|a| * |b|*cos
- float dot=Vector3.Dot（va，vb）;
- 两个标准化向量点乘结果为cos值
- 计算的夹角是最小夹角，（0~180）
- 对于标准化后的向量，方向完全相同，结果为1；完全相反，结果为-1；垂直结果为0
private void Demo05()
{
//dot两个向量夹角cos值
float dot=Vector3.Dot(t1.position.normalized,t2.position.normalized);
//计算夹角
angle=Mathf.Acos(dot)*Mathf.Red2Deg;
//如果两个向量夹角大于60度的限定条件
//if(angle>60)
//直接判断cos的值
if(dot<0.5)
}
叉乘
又称“叉积”或“外积”、
- 几何意义：结果为两个向量所组成面的垂直向量，模长为两向量模长乘积再乘夹角的正弦值
- Vector vector=Vector.Cross(a,b);
- 应用：
1、创建垂直于平面的向量
2、判断两条向量相对位置
private void Demo06()
{
//计算叉乘
Vector3 cross=Vector3.Cross(t1.position,t2.position);
//计算一圈夹角
if(cross.y<0)
{
angle=360-angle;
}
//叉乘所得向量的模长与角度关系：0~90度角
Vector3 cross=Vector3.Cross(a.normalized,b.normalized);
float angle=Mathf.Asin(cross.magnitue)* Mathf.Rad2Deg;
}
练习：计算物体右前方30度，10m远
float x=Mathf.Sin(30*Mathf.Deg2Rad)*10;
float y=Mathf.Cos(30*Mathf.Deg2Rad)*10;
Vector3 worldPoint=transform.TransformPoint(x,0,z);
三、欧拉角与四元数
欧拉角
- 使用三个角度来保存方位
- 欧拉角的三维向量没有方向，没有大小的概念
- x与z沿自身坐标系旋转，y沿世界坐标系旋转
- API：Vector3 eulerAngle=this.transform.eulerAngle;
- Inspector中的Transform中Rotation属性值为欧拉角的值
- 优点：
1、仅使用三个数表达方位，占用空间小
2、沿坐标轴旋转的单位为角度，符合人的思考方式
3、任意三个数字都是合法的，不存在不合法的欧拉角 - 缺点：
1、对于一个方位，存在多个欧拉角描述，因此无法判断多个欧拉角代表的角位移是否相同
2、为了保证任意方位的独一无二，Unity引擎限制角度范围，即沿x轴旋转限制在-90 ~ 90之间，沿Y轴与Z轴旋转限制在0 ~ 360之间
3、万向节死锁：物体沿X轴旋转正/负90度，自身坐标系Z轴与世界坐标系Y轴将重合，此时再沿Y轴或Z轴旋转时，将失去一个自由度
在万向节死锁的情况下，规定沿Y轴完成绕竖直轴的全部旋转，即此时Z轴旋转为0
private void Demo07()
{
//沿x轴旋转
this.transform.eulerAngles+=new Vector3(1,0,0);
this.transform.eulerAngles+=Vector3.up;
}
四元数
- Quaternion在3D图形学中代表旋转，由一个三位向量（X/Y/Z）和一个标量（W）组成。
- 旋转轴为V，旋转弧度为θ，如果使用四元数表示，则四个分量为：
1、x=sin（θ/2）* V.x
2、y=sin（θ/2）*V.y
3、z=sin（θ/2）*V.z
4、w=cos（θ/2） - X、Y、Z、W的取值范围是-1到1
- API：Quaternion qt=this.transform.rotation;
- this.transform.Rotate(Vector3 eulerAngles)
- 优点：
1、避免万向节死锁 - 缺点
1、难于使用，不建议单独修改某个数值
2、存在不合法的四元数
四元数用法
private void Demo08()
{
//旋转轴
Vector3 axis=Vector3.up;
//旋转弧度
float rad=60*Mathf.Deg2Rad;
Qutaternion qt=new Quaternion();
qt.x=Mathf.Sin(rad/2)*axis.x;
qt.y=Mathf.Sin(rad/2)*axis.y;
qt.z=Mathf.Sin(rad/2)*axis.z;
qt.w=Mathf.Cos(rad/2);
this.transform.rotation=qt;
//欧拉角转换为四元数
this.transform.rotation=Quaternion.Euler(0,60,0);
}
基本运算
1、与向量相乘
四元数左乘向量，表示将该向量按照四元数表示的角度旋转。
例如：
Vector3 point=new Vector3(0,0,10);
Vector3 newPoint=Quaternion.Euler(0,30,0)*point;
2、与四元数相乘
两个四元数相乘可以组合旋转效果
例如：
Quaternion rotation01=Quaternion.Euler(0,30,0)*Quaternion.Euler(0,20,0);
Quaternion rotation02=Quaternion.Euler(0,50,0);
rotation01与rotation02相同
练习：右前方10m远
//(0,0,10)向量根据当前物体的旋转而旋转
Vector3 vect=this.transform.rotation*new Vector3(0,0,10);
//vect 向量沿y轴旋转30度
vect=Quaternion.Euler(0,30,0)*vect;
//vect向量移动到当前物体的位置
vect=this.transform.position+vect;
思路：
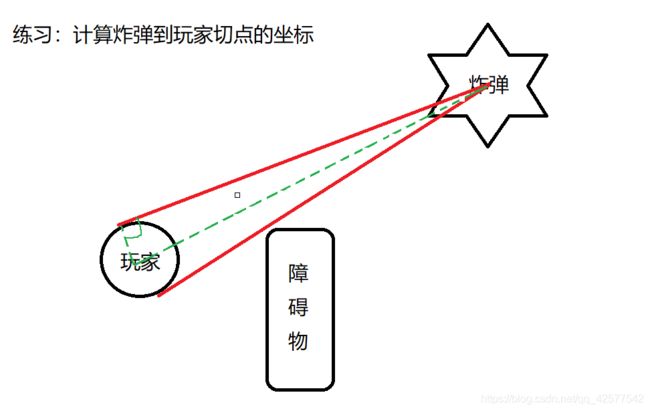
- 计算玩家到爆炸点的方向，半径长向量
- 根据夹角旋转向量
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class BoomDemo : MonoBehaviour {
public string playerTag = "Player";
private Transform playerTF;
private float radius;
private Vector3 leftTangent, rightTangent;
void Start()
{
GameObject playerGo = GameObject.FindGameObjectWithTag(playerTag);
playerTF = playerGo.transform;
radius = playerGo.GetComponent<CapsuleCollider>().radius;
}
//计算切点
private void CalculateTangent()
{
//爆炸点与玩家之间的距离
Vector3 PlayerToExplosion = this.transform.position - playerTF.position;
//爆炸点与玩家之间的半径长向量
Vector3 PlayerToExplosionDirection = PlayerToExplosion.normalized * radius;
//用反三角函数计算需要旋转的角度
float angle = Mathf.Acos(radius / PlayerToExplosion.magnitude) * Mathf.Rad2Deg;
//半径旋转至切点
//加上玩家的坐标，可以使切点跟随玩家移动
leftTangent = playerTF.position + Quaternion.Euler(0, -angle, 0) * PlayerToExplosionDirection;
rightTangent = playerTF.position + Quaternion.Euler(0, angle, 0) * PlayerToExplosionDirection;
}
void Update()
{
CalculateTangent();
Debug.DrawLine(this.transform.position, leftTangent);
Debug.DrawLine(this.transform.position, rightTangent);
}
}
世界坐标系下的图解
世界坐标系下的向量起点在世界坐标原点
- 爆炸点向量减去玩家向量，方向指向被减（图中蓝色虚线）
- 获取半径长的方向向量（图中紫色线）
- 旋转半径长向量（图中深蓝色线）
- 旋转后的向量加上玩家坐标，即可得到切点坐标（图中粉色线）
四、三维向量API
Vector3
重点静态方法
- Angle：由from和to两者返回一个角度。
float angle = Vector3.Angle(targetDir, forward); - ClampMagnitude ：返回向量的长度，最大不超过maxLength所指示的长度。
Vector3.ClampMagnitude(判断向量Vector3, 限制最大长度float); - Cross：两个向量的交叉乘积
- Distance：返回a和b之间的距离。
- Dot：两个向量的点乘积。
- Normalize：使向量的长度为1
Vector3.Normalize (new Vector3(6,3,2))；将自己设置为单位向量 - OrthoNormalize：使向量规范化并且彼此相互垂直。
Vector3.OrthoNormalize(ref basisA, ref basisB, ref basisC);
返回B,C向量与A垂直 - Project：投影一个向量到另一个向量。
static Vector3 Project(Vector3 vector, Vector3 onNormal); - Reflect：沿着法线反射向量。
返回的值是间接的相等的幅度，但其反射方向的向量 - MoveTowards：当前的地点移向目标。匀速移动到目标点
transform.position = Vector3.MoveTowards(transform.position起始点, target.position目标点, step移动速度); - Lerp：两个向量之间的线性插值。由快到慢，最终不能等于最终点
Vector3.Lerp(Vector3.zero起点位置, targetPos终点位置, curve.Evaluate(x)按照动画曲线移动);
四元数
静态变量
- identity 与世界坐标系统一
方法
- 欧拉角–>四元数
Quaternion.Euler(欧拉角) - 四元数–>欧拉角
Quaternion qt=this.transform.rotation;
Vector3 euler=qt.eulerAngles; - 轴/角旋转
this.transform.rotation=Quaternion.AngleAxis(50,Vector3.up); - z轴注视旋转，当前物体的位置不会改变
Vector3 dir=tf.position-this.transform.position;
this.transform.rotation=Quaternion.LookRotation(dir); - 差值旋转
this.transform.rotation=Quaternion.Lerp(this.transform.rotation,dir,0.1f); - 匀速旋转
this.transform.rotation=Quaternion.RotateTowards(this.transform.rotation,dir,0.1f); - 如果当前旋转角度接近目标旋转角度
if(Quaternion.Angle(this.transform.rotation,dir)<1)
{
this.transform.rotation=dir;
} - x轴注视旋转
this.transform.right=tf.position-this.transform.position;//一下子转过来
//从x轴正方向–>注视目标位置的方向
Quaternion dir=Quaternion.FromToRotation(Vector3.right,tf.position-this.transform.position);
this.transform.rotation=dir;
练习
根据用户输入的方向旋转角色，并向前移动
private void Update()
{
float hor=Input.GetAxis("Horizontal");
float ver=Input.GetAxis("Vertical");
if(hor!=0||ver!=0)
{
move(hor,ver);
}
}
private void move(float hor,float ver)
{
Quaternion dir=Quaternion.LookRotation(new Vector3(hor,0,ver));
this.transform.rotation=Quaternion.Lerp(this.transform.rotation,dir,Time.deltaTime*RotateSpeed);
this.transform.Translate(0,0,Time.deltaTime*MoveSpeed);
}
五、坐标系
1、World Space
- 世界坐标系：整个场景的固定坐标
- 作用：在游戏场景中表示每个游戏对象的位置和方向
2、 Local Space
- 物体坐标系：每个物体独立的坐标系，原点为模型轴心点，随物体移动而改变
- 作用：表示物体间相对位置与方向
3、 Screen Space
- 屏幕坐标系：以像素为单位，屏幕左下角为原点（0，0），右上角为屏幕宽、高，Z为到相机的距离
- 作用：表示物体在屏幕中的位置
4、 Viewport Space
- 视口坐标系：屏幕左下角为原点（0，0），右上角为（1，1），Z为到相机的距离
- 作用：表示物体在摄像机中的位置
坐标系转换
1、Local Space–>World Space
- transform.forward在世界坐标系中表示物体正前方
- transform.right在世界坐标系中表示物体正右方
- transform.up在世界坐标系中表示物体正上方
- transform.TransformPoint
转换点，受变换组件位置、旋转和缩放的影响 - transform.TransformDirection
转换方向，受变换组件旋转影响 - transform.TransformVector
转换向量，受变换组件旋转和缩放影响
2、World Space–>Local Space
- transform.InverseTransformPoint
转换点，受变换组件的位置、旋转、缩放的影响 - transform.InverseTransformDirection
转换方向，受变换组件旋转影响 - transform.InverseTransformVector
转换向量，受变换组件旋转和缩放影响
3、World Space<–>Screen Space
- Camera.main.WorldToScreenPoint
将点从世界坐标系转换到屏幕坐标系中 - Camera.main.ScreenToWorldPoint
将点从屏幕坐标系转换到世界坐标系中
4、World Space<–>Viewport Space
- Camera.main.WorldToViewportPoint
将点从世界坐标系转换到视口坐标系中 - Camera.main.ViewportToWorldPoint
将点从屏幕坐标系转换到世界坐标系中