数独小项目开篇:DFS解决数独难题
数独小项目开篇:DFS解决数独难题
- 前言
- DFS解决数独问题思路
- 代码实现细节
- 样例测试
- 总结
- Reference
前言
这周小刀是挺忙的,周末加班,哎,谁不是996呢?(打工魂燃烧吧~
这次我们来讲讲一个小项目——九宫格数独。
有很多关于这个问题的益智游戏,但是它的解法其实也可以用我们之前讲的 DFS 来解决。
不过我这次讲的是个小项目,那自然会较为完整一些。在DFS算法实现数独的基础上,利用图像处理来将一张数独题目的图片(可以从软件上截图获取)进行数据读取:即给我一张数独的图片,我就能给出这道数独题目的解法。
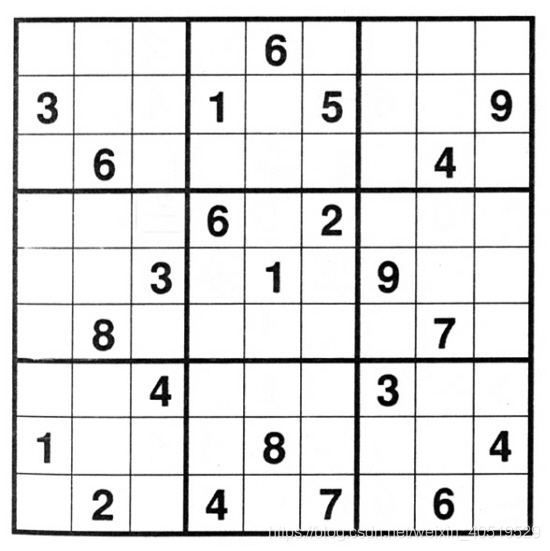
比如我们拿到上面的这张图,我们可以利用软件将它转化为数组,这样就可以运行既定的数独求解算法,得到解。
这其中涉及了图像处理,模板匹配等技术,当然我们的核心是数独求解,别给我整些花里胡哨的
这个项目的灵感来自于我去年在GITHUB上看到的一个项目,那个博主也完成了类似的工作,还写了UI界面,使得整个项目很完整,Nice
接下来我们也分部分来讲解这个小项目的完成过程吧
DFS解决数独问题思路
其实数独问题很适合来进行DFS的全局解空间搜索,只要有解,那我们就可以找得到,因为最直接的做法就是暴力求解,我尝试所有的可能数字组合,总会get到答案,会有那么一天!
首先我们来拆解问题:
给定一个数独题目,有些位置有数,有些位置没有数,没有数的位置需要我们填进数字。而九宫格数独的规则是:每行每列,每一个格子(包含九个数)内,都是数字1-9,且只出现一次。

按照我们之前讲的思路:我们DFS的起点肯定是第一个待填的格子,循环1-9,判断是否可以在这个位置填下,如果可以,假设我填了数字5,更新一些状态变量,然后递归到下一个待填的位置,继续循环数字,找合适的填下,算法结束的标志就是所有待填的格子都被我填完了。
这个问题其实核心操作很少,主要是一些数据读取的过程和状态变量的设置。
代码实现细节
首先我们需要一个存储待填格子行列坐标的数组:
point=[] # 待填入数字的格的坐标
然后我们有三个判断规则,即每行每列每个宫格都要没有重复,我们来创建状态变量:
M=9
row=[[False for _ in range(M)] for _ in range(M)]
col=[[False for _ in range(M)] for _ in range(M)]
Mat=[[[False for _ in range(M)]for _ in range(3)] for k in range(3)]
这里row,col都是M*M的数组(M只要大于9都可以),表示每行可能出现的各种数字标记,一共就9行,每行9个数字,所以是 9 * 9的数组,而宫格是9个,一共三行三列,每个宫格9个数字,所以是3 * 3 * 9的数组。
假设我们的输入格式是下面这样,即待填位置的数用0表示:
8 0 0 0 0 0 0 0 0
0 0 3 6 0 0 0 0 0
0 7 0 0 9 0 2 0 0
0 5 0 0 0 7 0 0 0
0 0 0 0 4 5 7 0 0
0 0 0 1 0 0 0 3 0
0 0 1 0 0 0 0 6 8
0 0 8 5 0 0 0 1 0
0 9 0 0 0 0 4 0 0
我们可以先读取数据然后初始化状态变量
Sudoku=[] # 保存数据
for i in range(9):
Sudoku.append(list(map(int,input().split())))
for i in range(9):
for j in range(9):
num=Sudoku[i][j]
if num!=0:
row[i][num]=True
col[j][num]=True
Mat[i//3][j//3][num]=True
else:
point.append((i,j))
这里i,j表示行列坐标,当位于i行j列的数不是0,即已经填入的数,我们更新其所在行列在当前数字下的状态变量,九宫格这里注意要整除3,得到所在九宫格的正确行列数。
如果是0,则保存其行列位置到point数组,以便后续使用
还记得上次在斐波那契数列讲到的DFS该注意的几点嘛?(小刀打开了之前的码稿……
大致三个点:
- 第一个是搜索策略,这是核心算法,自不用多说
- 第二个是循环的前后参量传递,即我走过的路我不走了,或者通过一条失败的路pass掉其他n条类似的路直接不走,节省时间空间。
- 第三个是退出条件,没有退出条件,就是无限循环,Happy Ending!
接下来便是DFS的核心函数了,大家可以按照上面讲过的思路比对代码的实现,就会容易理解很多。
def dfs(num):
"""
Function: DFS for Sudoku
Arg:
num(int):the number of boxes that need to be solved
"""
nonlocal Sudoku, row, col, Mat, flag, point
if flag:
return
# ending condition
if num == -1: # 填完全部
# 打印结果
flag = True
return
# recursion step
for c in range(1, 10):
x, y = point[num]
if (row[x][c] == False) and (col[y][c] == False) and (Mat[x//3][y//3][c] == False):
# set state
row[x][c] = col[y][c] = Mat[x//3][y//3][c] = True
Sudoku[x][y] = c
dfs(num-1)
# clear state
row[x][c] = col[y][c] = Mat[x//3][y//3][c] = False
Sudoku[x][y] = 0
这里递归的变量是待填格子的数量,当格子数量为-1时,即表示已经填完所有的格子,解答完毕。令flag标志为True,直接退出还在进行的其他递归状态。
再理一下思路:如果还没填完,则读取point里面保存的当前第num个格子的行列位置,遍历数字1-9,如果当前行,当前列,当前宫格都还没出现过该数字,则表示可以填下,令该位置数据为该数字,令num-1,继续递归。
记得退出该数字的递归时,要清除选定该数字所标记的状态变量和Sudoku数组数据,才不会影响到其他递归状态喔~
样例测试
我们来看刚才的那组数据的测试结果:
>>> Sudoku()
8 0 0 0 0 0 0 0 0
0 0 3 6 0 0 0 0 0
0 7 0 0 9 0 2 0 0
0 5 0 0 0 7 0 0 0
0 0 0 0 4 5 7 0 0
0 0 0 1 0 0 0 3 0
0 0 1 0 0 0 0 6 8
0 0 8 5 0 0 0 1 0
0 9 0 0 0 0 4 0 0
60 boxes to solve:
8 1 2 | 7 5 3 | 6 4 9
9 4 3 | 6 8 2 | 1 7 5
6 7 5 | 4 9 1 | 2 8 3
---------------------
1 5 4 | 2 3 7 | 8 9 6
3 6 9 | 8 4 5 | 7 2 1
2 8 7 | 1 6 9 | 5 3 4
---------------------
5 2 1 | 9 7 4 | 3 6 8
4 3 8 | 5 2 6 | 9 1 7
7 9 6 | 3 1 8 | 4 5 2
Used 0.29929 s
差不多用了0.3s,还是可以接受的。
再来看我们引言用到的图片的数独:
>>> Sudoku()
58 boxes to solve:
4 9 2 | 8 6 3 | 7 1 5
3 7 8 | 1 4 5 | 6 2 9
5 6 1 | 2 7 9 | 8 4 3
---------------------
7 1 5 | 6 9 2 | 4 3 8
2 4 3 | 7 1 8 | 9 5 6
9 8 6 | 3 5 4 | 1 7 2
---------------------
6 5 4 | 9 2 1 | 3 8 7
1 3 7 | 5 8 6 | 2 9 4
8 2 9 | 4 3 7 | 5 6 1
Used 0.06116 s
这道题看来对计算机来讲比较好做,只用了0.06s,反正我是做不出来(
总结
下回我们来看看怎么从图片里直接读取数据,就不用看着图一个数字一个数字敲了,一不小心中途按了Enter的话强迫症当场去世。
欲知后事如何,请听下回分解!
![]()
![]()
Reference
[1] 数独小项目开篇:DFS解决数独难题