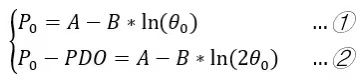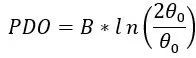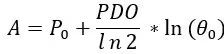让你彻底理解信用评分卡原理（Python实现评分卡代码）
逻辑回归已经在各大银行和公司都实际运用于业务，但是很多文章都讲得一知半解，所以本文力求阐述出清晰的评分卡原理文章。之前已经讲解了逻辑回归和sigmod函数的由来、逻辑回归(logistics regression)原理-让你彻底读懂逻辑回归，本文致力于让大家彻底弄懂评分卡的原理和实现。
一、评分卡原理
根据逻辑回归原理，客户违约的概率p有如下式子：
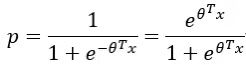
其中x为客户特征,θ为特征系数，上式整理得：
即
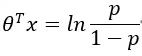
违约概率和正常概率的比值称为比率（Odds），即：
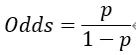
所以
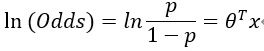
设评分卡的评分Score为：
或
其中A、B是正常数，在风控中一般分数越高信用越好风险越低。所以B前面取负号，让违约的概率越高分数越低。由中学知识可知，两个方程联立可求出两个未知数。为求出A、B的具体值，有如下两个假设：
1.假设比率为θ0时的基准分为P0。
2.假设比率翻倍（2θ0）时分数的变动值为PDO。
把θ0、P0、PDO代入评分公式得：
①-②得：
即
最终解得：
将③代入①得：
即
假设θ0=0.001时，P0=600，PDO=40。
则
即
或
则
其中x1、x2、xn等是出现在最终模型的入模变量。由于一些入模变量进行了WOE编码，可以将评分写成对应woe的形式。
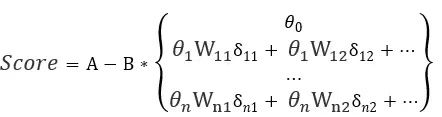
其中θi为第i个特征的系数，Wij为第i个特征第j个分箱的WOE值，是0、1逻辑变量，当客户对应特征的取值落在该分箱时为1否则为0。所以最终的评分卡形式如下：
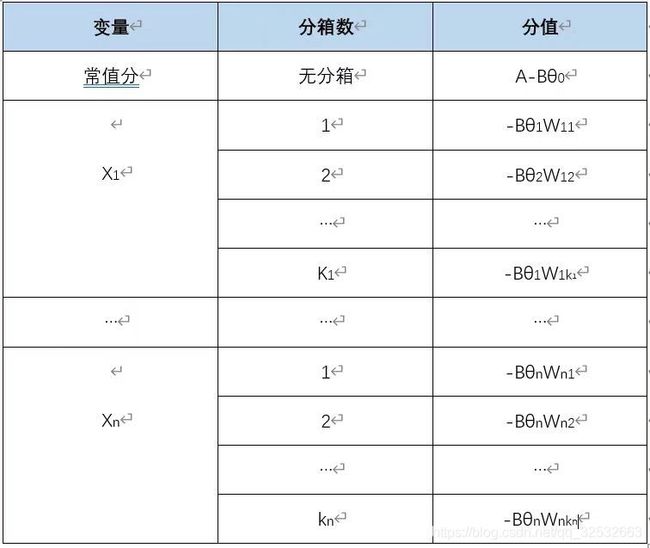
二、评分卡Python实现
从评分卡原理的分析中知，得到客户的最终得分有两个计算公式：
或
如果已经通过逻辑回归的训练得到客户的违约概率，且只想得到客户的最终得分。可把违约概率P代入第一个式子即可以得到客户得分。
1 根据客户违约概率计算客户得分
具体计算代码如下：
def Prob2Score(prob, A, PDO):
#将概率转化成分数且为正整数
y = np.log(prob/(1-prob))
return int(A-PDO/np.log(2)*(y))
A, PDO = 201.35,40
score['prob2score'] = score['predict'].apply(lambda x: Prob2Score(x, A, PDO))
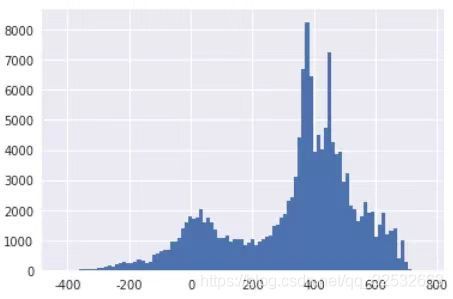
plt.hist(X_f_1['score'],bins=100)
plt.show()
其中Prob2Score是根据第一个公式写的函数，只要输入违约概率prob、A和PDO的值即可计算客户得分,得到所有样本的得分分布如下：
2 根据分箱WOE和特征系数计算客户得分
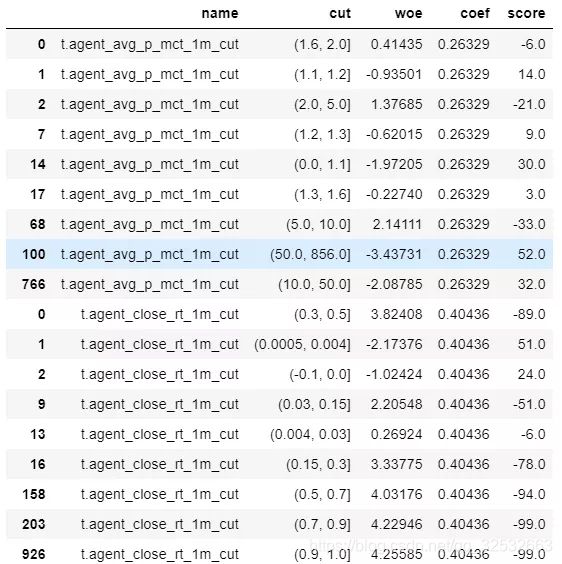
计算评分卡时先不考虑常值分A-Bθ0的值，只把每个特征对应分箱的分值算出。根据最终评分卡形式编写Python脚本如下，可得到标准评分卡。
def var_card(cut,woe,coef,B):
import warnings
warnings.filterwarnings('ignore')
w1 = pd.DataFrame({
'cut':cut,'woe':woe})
w2 = w1.drop_duplicates(subset=['cut','woe'],keep='first')
w2['name'] = cut.name
w2['coef'] = coef[woe.name][0]
w2['score'] = round(-w2['woe']*w2['coef']*B,0).astype('int64')
w3 = w2[['name','cut','woe','coef','score']]
return w3
def score_card(card_name,data,B,coef):
score_cards = pd.DataFrame({
'name':[0],'cut':[0],'woe':[0],'coef':[0]})
data = data
for i in range(card_name.shape[0]):
cut = data[card_name.iloc[i,0]]
woe = data[card_name.iloc[i,1]]
coef = coef
card = var_card(cut,woe,coef,B)
if card.shape[0]<20:
score_cards = score_cards.append(card)
score_cards_final = score_cards[['name','cut','woe','coef','score']]
score_cards_final = score_cards_final.iloc[1:,:]
return score_cards_final
card_name = pd.DataFrame({
'cut':columns_final_cut,'woe':columns_final_woe})
data = data
A, PDO, B = 201.35,40,40/np.log(2)
coef = coef_1
score_card_1 = score_card(card_name,data,B,coef)
其中card_name中存储每个特征对应分箱的woe值，data表示原始数据，B是公式中的常数，coef表示特征对应系数。该计算公式只是我为了熟悉原始计算公式编写，后续会进行代码优化，请悉知，得到结果如下：
如果想根据评分卡对应分段的值得到最终得分，可在Python中输入如下代码：
def all_score(score_card,data,A,B,θ0):
var_name = score_card[['name']].drop_duplicates(subset=['name'],keep='first')
names = ['a']
for i in range(var_name.shape[0]):
sub = score_card[score_card['name']==var_name.iloc[i,0]]
sub_1 = sub[['cut','score']]
sub_1.rename(columns={
'cut':sub['name'][0], 'score':sub['name'][0]+'_score'}, inplace = True)
data = data.merge(sub_1, on=sub['name'][0],how='left')
names.append(sub_1.columns[1])
names = names[1:]
score_model = data[names]
score_model['woe_score'] = score_model.apply(lambda x:x.sum(), axis = 1)
data['TOTALSCORE'] = score_model['woe_score']+A-B*θ0
return data
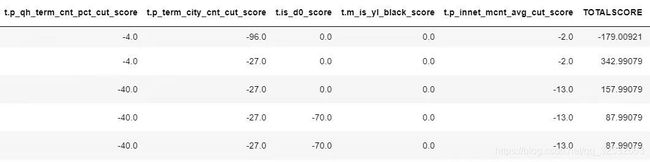
score_1 = all_score(score_card_1,data,201.35,40/np.log(2),θ0=0.001)
其中score_card_1表示标准评分卡，data表示原始数据，A、B、θ0详见上文中评分卡原理。得到结果如下：
至此，逻辑回归的原理和代码阐述完毕，感兴趣的同学可以自己根据公式，写出对应的Python代码。
你可能感兴趣:
用Python绘制皮卡丘
用Python绘制词云图
Python人脸识别—我的眼里只有你
Python画好看的星空图（唯美的背景）
用Python中的py2neo库操作neo4j，搭建关联图谱
Python浪漫表白源码合集（爱心、玫瑰花、照片墙、星空下的告白）
