牛客 每日一题 8 Shortest Path 题解（思维）

题目链接

题目大意

给你一棵 n 个节点的树（保证 n 是偶数），你需要将 n 个节点分为 n/2 个点对，使得每个点对的两个点的距离的和最小。

题目思路

这是一个打着图论题幌子的思维题。。。。

首先我们可以通过观察得到以下几点：

首先，在最短的距离和之中一条边一定不会被覆盖两次，如图，我们一定可以找到一种方法来交换配对，把重复的边去掉（其他的边是不会变的）。也就是说对于一条边来说，其实只有选和不选两种可能。

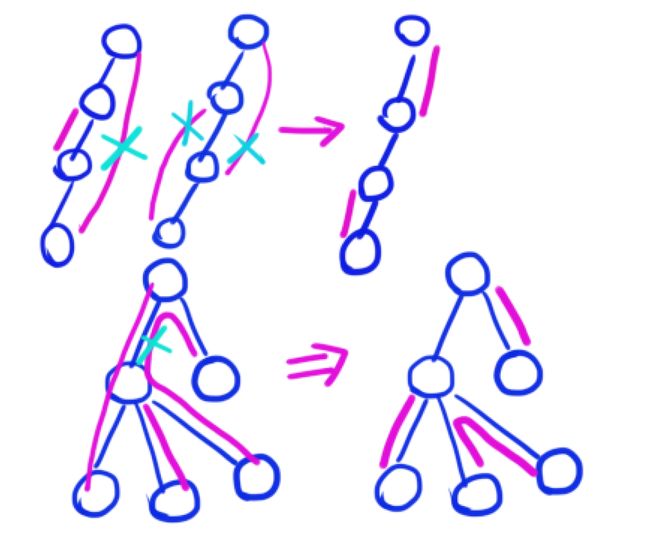
第二，对于一个点x，它子树中的点一定会尽量在子树中找到匹配的点内部消化掉（要么连父亲要么连兄弟），只有根是有可能会往上找一个点来匹配（不然又会出现重复覆盖一条边的情况）。

那么如果我们不去想点怎么两两配对而是来考虑每个边选不选——对于当前点 x，如果它的子树大小（包括它自己）有偶数个点，那么肯定在子树里面就互相连完了，它不需要向上连；如果是奇数个点，x 就需要去匹配上面的点了，所以 x 向它父亲连的边就要选。然后就没有然后啦！

这个题告诉我们，要善于对题目进行转换，题目让匹配点这个操作是比较困难的，所以我们可以选择通过选边来替代它，问题就简单了。

代码

#include
#include
using namespace std;
typedef long long ll;
const int maxn=1e4+5;
ll ans;
int t,n,cnt,head[maxn],tot[maxn],u,v,w;
struct node{
     
	int	to,next,w;
}e[maxn<<1];
void add(int u,int v,int w){
     
	e[++cnt].to=v;
	e[cnt].next=head[u];
	e[cnt].w=w;
	head[u]=cnt;
}
void init(){
     
	memset(head,0,sizeof(head));
	memset(e,0,sizeof(e));//其实这个不要清空 
	cnt=0,ans=0;
}
void dfs(int son,int fa,int len){
     
	tot[son]=1;
	for(int i=head[son];i;i=e[i].next){
     
		if(e[i].to!=fa){
     
			dfs(e[i].to,son,e[i].w);
			tot[son]+=tot[e[i].to];
		}
	}
	if(tot[son]%2){
     //子树（包括自己）为奇数个数 
		ans+=len;
	}
}
int main(){
     
	scanf("%d",&t);
	while(t--){
     
		init();
		scanf("%d",&n);
		for(int i=1;i<=n-1;i++){
     
			scanf("%d %d %d",&u,&v,&w);
			add(u,v,w),add(v,u,w);
		}
		dfs(1,0,0);
		printf("%lld\n",ans);
	}
	return 0;
}

参考链接 https://ac.nowcoder.com/discuss/398540