机器学习 —— KNN

**

机器学习 —— KNN

**
本文致力于将机器学习相关知识简单化的呈现给小白，文章内有错误的地方希望读者能指出。大家一起共同学习，共同进步！

目录

一、对KNN算法的理解

二、算法步骤

三、算法实战

四、补充内容

**

一、对KNN算法的理解

对KNN算法最简单的理解就是采用测量不同特征值之间的距离方法进行分类。
通俗理解，在一个平面上面有很多棋子，这些棋子有两种颜色，红色和绿色，红色的棋子和绿色的棋子位于平面上面不同的位置，这个时候，突然有个新来的棋子，不知道该棋子的颜色，可是怎么能确定该棋子的颜色呢，这是KNN算法要做的事情–预测。而该算法的方法–距离预测，通过计算未知棋子与已知平面的上的所有的棋子距离，选取离未知棋子近的k个棋子，分别计算这个k个棋子两种颜色出现的频率，频率出现最高的颜色作为预测结果。
当然，上面这个例子有个前提，棋子摆放是随机的，可以是空中随机落下，位置具有随机性，如果棋子被安排了，用KNN进行预测，结果可能就…
每一个棋子其实就是样本，颜色就是特征，红色和绿色就是标签，选取样本需要具有合理性，特征需要突出，与预测结果的关联度当然越高越好。

二、算法步骤

1.处理数据（很关键！！！）
2.计算未知点与所有已知点之间的距离（计算方法后面有）
3.将距离进行排序，选取与未知点距离最近的k个点
4.计算k个点中出现频率最高的类别
5.此类别作为预测结果

怎么计算距离？
常用欧式距离，公式如下：

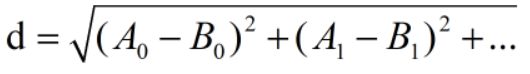
例：
A(0,0),B(2,3)，计算A、B之间距离如下：
$$d=\sqrt{(0-2{)}^2+(0-3{)}^2}.$$

三、算法实战

import numpy as  np
from sklearn.neighbors import KNeighborsClassifier

train_x = [[0,0],[2,3],[1,1],[2,2],[5,5],[6,7],[6,6],[4,5]]
train_y = ['A','A','A','A','B','B','B','B']
x = [[0,1],[2,0]]
k = 2

def knn(x,train_x,train_y,k):
    train_x = np.array(train_x)
    x = np.array(x)
    knn_clf = KNeighborsClassifier(n_neighbors=k)    #分类器
    knn_clf.fit(train_x, train_y)                    #进行拟合
    print("测试准确度：%f"%(knn_clf.score(train_x, train_y)))  #这里其实应该用测试的数据来计算准确度
    print("预测结果：%s"%(knn_clf.predict(x)))


if __name__== "__main__":
    knn(x,train_x,train_y,k)
'''
    测试准确度：1.000000
    预测结果：['A' 'A']
'''

以上是最简单的KNN代码，用以理解，可是看看这段代码，有一个疑问，这个k从哪来的，为什么等于2，等于3行不行？下面继续深入学习KNN。
k的选取是KNN算法中很关键的一步，这直接影响准确度，一般k不会超过20，至于怎么取一个好的k值，当然由计算机自己完成选择这个过程。

import numpy as  np
from sklearn.neighbors import KNeighborsClassifier

train_x = [[0,0],[2,3],[1,1],[2,2],[5,5],[6,7],[6,6],[4,5]]
train_y = ['A','A','A','A','B','B','B','B']
x = [[0,1],[2,0]]

def knn2(x,train_x,train_y):
    train_x = np.array(train_x)
    x = np.array(x)
    best_score = 0
    for method in ["uniform", "distance"]:
        for k in range(1, 3):
            for p in range(1, 6):
                knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method, p=p)
                knn_clf.fit(train_x, train_y)
                score = knn_clf.score(train_x, train_y)  #这里其实应该用测试的数据来计算准确度
                if score > best_score:
                    best_k = k
                    best_score = score
                    best_p = p
                    best_method = method                   #进行拟合
    print("最优k值%d"%(best_k))
    print("最优权重方法%s" % (best_method))
    print("最优p值%d" % (best_p))
    print("测试准确度：%f"%(best_score))
    print("预测结果：%s"%(knn_clf.predict(x)))

if __name__== "__main__":
    knn2(x,train_x,train_y)
'''
最优k值1
最优权重方法uniform
最优p值1
测试准确度：1.000000
预测结果：['A' 'A']
'''

下面介绍一下**knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method, p=p)**这个函数的用法
n_neighbors：输入参数为k值，一般不超过20
weights ：权重方法，uniform表示所有距离值的权重都一样，distance表示距离的导数作为权重，则距离越近，权重系数越大，影响越大
p：表示距离计算方法，欧氏距离公式和曼哈顿距离。这个参数默认为2，默认使用欧式距离公式进行距离度量。设置为1，使用曼哈顿距离公式进行距离度量。

四、补充内容

在这里主要讲一下数据处理中归一化数值的重要性，由欧式距离公式可以看出，任何一个特征量如果值特别大，那么预测结果几乎仅有这个特征决定，万一这个特征对于实际结果的影响不大，那么准确度将会特别低，为了防止这种情况的出现，数据处理部分我们一般会归一化处理，把数值都统一为0-1或者-1-1之间。

    for i in range(len(train_x[0])): #归一化
        if np.max(train_x[i]) - np.min(train_x[i]) == 0:
            train_x[i] = 0
        else :
            train_x[i] = (train_x[i] - np.min(train_x[i])) / (np.max(train_x[i]) - np.min(train_x[i]))

通常在进行训练的时候，会加上归一化的代码