五次多项式换道曲线模拟小车换道算法的Matlab实现

声明：本项目来自于B站：https://www.bilibili.com/video/BV1dv411W77J
刚跟着学习不久，跟着将代码打了出来，放在这里一是自己做个笔记，二是看到优秀的学习内容，帮忙推广一下了，up主在B站的视频还在持续更新中，我们大家一起搬着小板凳去学习啊。
matlab绘制效果如下：

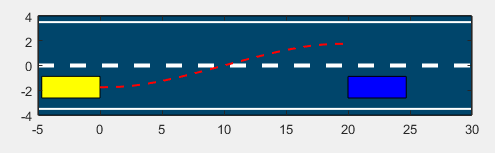
（黄色、蓝色代表两辆小车，红色虚线代表着黄色车辆的换道轨迹(基于五次多项式曲线)）。
一、函数介绍
多项式优化曲线有三次、五次、七次多项式曲线，能够满足我们绝大多数的车辆运动解析；
构建五次多项式曲线，可以解析物体的位移、速度、加速度三种状态值：
五次多项式形式如下：

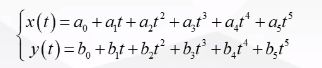
x、y代表小车位移是关于时间t的五次多项式，对其一阶二阶求导便得到速度、加速度状态曲线：

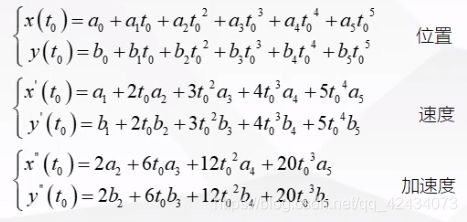
状态曲线是随时域变化的，我们设t0为小车的初始时刻，t1为终点时刻，解算位置、速度、加速度状态方程，并构建成矩阵形式（X、Y分别代表了纵向与横向的运动）：

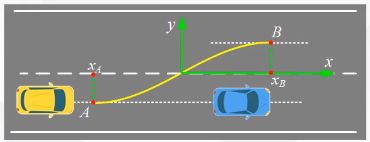
其实是很容易理解的，我们可以参考下图增加我们的理解，初始时刻t0，位置点为A，终点时刻t1，位置点为B，我们知道A点的车辆位置、速度、加速度，然后我们要规划一条路线到达B点，我们对于B点有期望的速度、加速度，这样我们就能根据期望值解算出状态变换的曲线：

二、下面附上代码做出解释：

clc
clear
close all
%% 场景定义
%换道场景路段与车辆相关参数的定义
d=3.5; %车道标准宽度
len_line=30; %直线段长度
W=1.75; %车宽
L=4.7; %车长
x1=20; %1号车x坐标

%车辆换到初始状态与终点期望状态：
t0=0;
t1=3;
state_t0=[0,-d/2;5,0;0,0]; %x,y; vx,vy; ax,ay;
state_t1=[20,d/2;5,0;0,0];
x2=state_t0(1); %在旁边放着一辆参考车辆

%% 画场景的示意图
figure(1)
% 画灰色路面图
GreyZone=[-5,-d-0.5;-5,d+0.5;len_line,d+0.5;len_line,-d-0.5];
fill(GreyZone(:,1),GreyZone(:,2),[0/255 69/255 107/255]);
hold on

%画小车
fill([x1,x1,x1+L,x1+L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],‘b’) %1号小车
fill([x2,x2,x2-L,x2-L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],‘y’)

%画分界线
plot([-5,len_line],[0,0],‘w–’,‘linewidth’,3); %分道线
plot([-5,len_line],[d,d],‘w’,‘linewidth’,1.5); %左边界
plot([-5,len_line],[-d,-d],‘w’,‘linewidth’,1.5); %右边界

% 设置坐标轴范围
axis equal
set(gca,‘Xlim’,[-5 len_line]);
set(gca,‘Ylim’,[-4,4]);

%% 五次多项式轨迹

%计算A和B两个系数矩阵
X=[state_t0(:,1);state_t1(:,1)];
Y=[state_t0(:,2);state_t1(:,2)];
T=[t0^5 t0^4 t0^3 t0^2 t0 1;
5t0^4 4t0^3 3t0^2 2t0 1 0;
20t0^3 12t0^2 6t0 2 0 0;
t1^5 t1^4 t1^3 t1^2 t1 1;
5t1^4 4t1^3 3t1^2 2t1 1 0;
20t1^3 12t1^2 6t1 2 0 0];
A=T\X;
B=T\Y;

% 将时间从t0到t1离散化，获得离散时刻的轨迹坐标
t=(t0:0.1:t1);
path=zeros(length(t),4);%1-4列分别存放x,yvx,vy
for i=1:length(t)
%纵向位置坐标
path(i,1)=[t(i)^5, t(i)^4, t(i)^3, t(i)^2, t(i), 1] * A;
%横向位置坐标
path(i,2)=[t(i)^5, t(i)^4, t(i)^3, t(i)^2, t(i), 1] * B;
%纵向速度
path(i,3)=[5t(i)^4, 4t(i)^3, 3t(i)^2, 2t(i), 1, 0] * A;
%横向速度
path(i,4)=[5t(i)^4, 4t(i)^3, 3t(i)^2, 2t(i), 1, 0] * B;
end

% 画换道轨迹
plot(path(:,1),path(:,2),‘r–’,‘linewidth’,1.5);

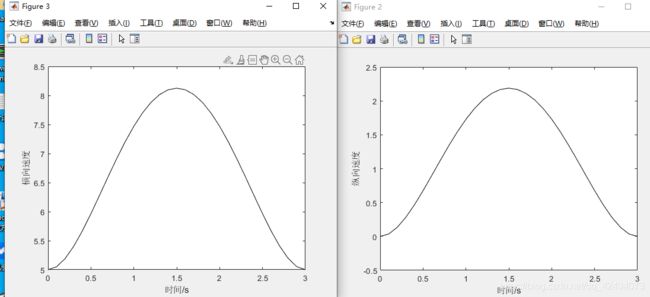
%% 分析速度
figure
plot(t,path(:,4),‘k’);
xlabel(‘时间/s’);
ylabel(‘纵向速度’);
figure
plot(t,path(:,3),‘k’);
xlabel(‘时间/s’);
ylabel(‘横向速度’);

运行后可以画出文章开头的效果，并且打印出了横向、纵向速度变化：