Radon变换入门matlab CT原理
http://hi.baidu.com/hi9394/blog/item/0d492b8bfd714700c8fc7aa9.html
简介
图像投影,就是说将图像在某一方向上做线性积分(或理解为累加求和)。如果将图像看成二维函数f(x, y),则其投影就是在特定方向上的线性积分,比如f(x, y)在垂直方向上的线性积分就是其在x轴上的投影;f(x, y)在水平方向上的线积分就是其在y轴上的投影。通过这些投影,可以获取图像在指定方向上的突出特性,这在图像模式识别等处理中可能会用到。
Radon变换(拉东变换),就是将数字图像矩阵在某一指定角度射线方向上做投影变换。这就是说可以沿着任意角度theta来做Radon变换。
实例
% By lyqmath
% Dalian University of Technology
% School of Mathematical Sciences
clc; clear all; close all;
I = zeros(256, 256);
[r, c] = size(I);
I(floor(1/5*r:4/5*r), floor(3/5*c:4/5*c)) = 1;
figure;
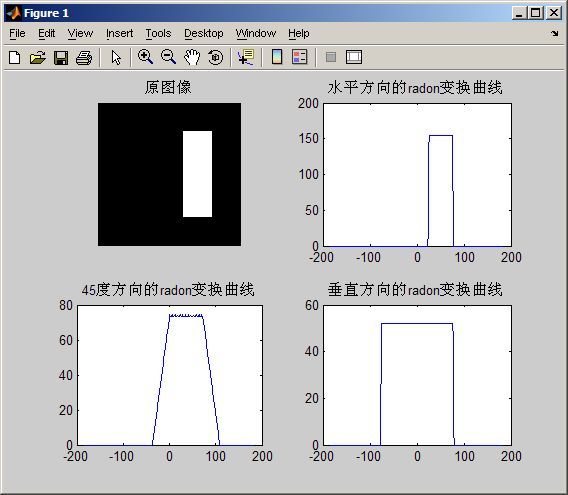
subplot(2, 2, 1); imshow(I); title('原图像');
[R, xt] = radon(I, [0 45 90]); % 在0、45、90度方向做radon变换
subplot(2, 2, 2);
plot(xt, R(:, 1));
title('水平方向的radon变换曲线');
subplot(2, 2, 3);
plot(xt, R(:, 2));
title('45度方向的radon变换曲线');
subplot(2, 2, 4);
plot(xt, R(:, 3));
title('垂直方向的radon变换曲线');
结果
总结
由于radon变换将图像变换到按角度投影区域,和有名的hough类似,可以应用与检测直线。个人认为,通过将图像矩阵在多角度做积分投影,再对得到的数据做统计分析,可以确定出图像的一些基本性质。
==================附======================
I = zeros(100,100);
I(25:75, 25:75) = 1;
imshow(I)
[R,xp] = radon(I,[0 45]);
figure; plot(xp,R(:,1)); title('R_{0^o} (x\prime)')
theta = 0:180;
[R,xp] = radon(I,theta);
imagesc(theta,xp,R);
title('R_{\theta} (X\prime)');
xlabel('\theta (degrees)');
ylabel('X\prime');
set(gca,'XTick',0:20:180);
colormap(hot);
colorbar
结果:
变换后
=====================逆变换=====================
I = zeros(100,100);
I(25:75, 25:75) = 1;
P=I;
imshow(P)
theta1=0:10:170;[R1,xp]=radon(P,theta1); %存在18个角度投影
theta2=0:5:175;[R2,xp]=radon(P,theta2); %存在36个角度投影
theta3=0:2:178;[R3,xp]=radon(P,theta3); %存在90个角度投影
figure,imagesc(theta3,xp,R3);colormap(hot);colorbar;
xlabel('\theta');ylabel('x\prime'); % 定义坐标轴
I1=iradon(R1,10);
I2=iradon(R2,5);
I3=iradon(R3,2);
figure,imshow(I1),title('I1');
figure,imshow(I2),title('I2');
figure,imshow(I3),title('I3');
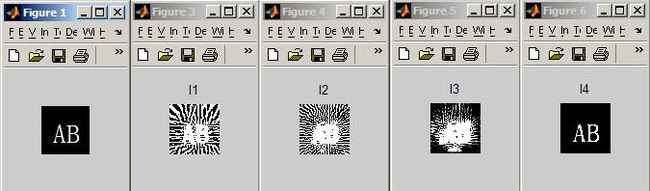
I1、I2、I3结果
==========================反变换====================
I = imread('mm.JPG');
I = rgb2gray(I);
P=I;
imshow(P)
theta1=0:10:170;[R1,xp]=radon(P,theta1); %存在18个角度投影
theta2=0:5:175;[R2,xp]=radon(P,theta2); %存在36个角度投影
theta3=0:1:179;[R3,xp]=radon(P,theta3); %存在90个角度投影
figure,imagesc(theta3,xp,R3);colormap(hot);colorbar;
xlabel('\theta');ylabel('x\prime'); % 定义坐标轴
I1=iradon(R1,10); % 开始反变换,还原图像
I2=iradon(R2,5);
I3=iradon(R3,1);
figure,imshow(I1),title('I1');
figure,imshow(I2),title('I2');
figure,imshow(I3),title('I3');
k=input('Your Thresh(0,1):')
thres1=max(I3(:))*k %maybe 0.5 is perfect
figure,imshow(I3>thres1),title('I4');
结果:
原图、I1、i2、i3、i4(0.5threshold)
==================这也是螺旋CT成像原理了 by hi9394===============
关键词:CT原理