机器学习 ——logistic回归

机器学习 ——logistic回归

**
本文致力于将机器学习相关知识简单化的呈现给小白，文章内有错误的地方希望读者能指出。大家一起共同学习，共同进步！
**

目录

一、一些基本概念的理解

二、算法介绍以及理解

三、几种优化方法的介绍和代码

**

一、一些基本概念的理解

在讲述算法前，先介绍一下几个基本概念，感觉这些概念比较关键，不管在机器学习还是在深度学习，对于理解算法和优化代码都是很关键的内容，废话不多说，开干！（读者若是感觉还缺少些重要概念，希望能在评论区给出，后面再来完善）
1.训练集：用来训练的样本集，通过这些样本的训练不断找到最优参数。
2.测试集：用来测试当前学习网络的准确度。这一步相当于负反馈环节，机器在学习的过程中，如何判断这一轮的学习方向是否正确，以及下一步方向如何，是用此时的网络对测试集进行测试，得出准确度和损失，对损失进行优化，进行下一轮的训练。
3.验证集：最后用来验证网络准确度的样本集。为什么会出现验证集？要知道机器是模仿人在学习，举一个人在学习过程中的例子，如果你将要的考一门课，而这门课是有一个考题库，平时可以通过题库来训练，相信你经过题库训练一定能得出好成绩，但是如果出的题目是题库外的，那就不一定了。我们进行机器学习和深度学习目的不是为了学习好这些样本，更关键是用来预测未来新的样本的标签，所以真正来评价机器学习的好坏程度，应该用没有经过训练的数据——验证集。
4.学习率：学习程度。同样也是类比人的学习，接触一个新的事物，刚开始学习可以比较快，到后面深入学习的时候学习就需要慢慢学习。机器也是如此，刚开始进行参数优化的时候，步子可以迈大一点，一下子啃一大块，即将逼近最优参数的时候也是快胜利的时候，就需要慢一点，慢慢逼近，这个时候如果一大步，可能就会出现迈过，会一直徘徊在终点两边。
5.损失函数：简单理解就是失误率。损失函数有很多种，常用的是交叉熵损失函数（这些后面单独进行介绍）
6.重要函数：Sigmiod函数。
这个函数主要是用来预测输出的，输出预测的分类。公式如下：
$$\sigma (z)=1/(1+e^{-z})$$

可以看出，这个函数类似单位阶跃函数，但是它上升和下降的并没有那么陡，这让我们更好处理。我们可以以Z=0作为分界线，Z>0那么输出值>0.5，我们可以将这分为一类；Z<0那么输出值<0.5，这可以划为另一类。Logistic回归分类主要用的输出函数就是sigmoid函数。

二、算法介绍以及理解

logistic回归就是用来分类的一种算法，简单理解就是，类似下棋，刚开始红黑双方各占据一边，logistic的目的就是作为楚汉分界线，把两方兵力分开，这条线要最优，不能乱来，混入间谍，算法就是想要找到最优的这条线，把不同的事物分开。
先看下面公式：
$$z=w(0)x(0)+w(1)x(1)+...+w(n)x(n)$$
$$predict=sigmoid(z)$$
x是输入特征向量，w是权重，学习的内容就是w权重的调整，算法就是为了寻求最好的权重，优化要做的是如何去找最优参数和如何最快去寻求。

三、几种优化方法的介绍和代码

1.梯度上升法
首先介绍梯度上升这一最优化算法。要想寻求某一函数的最大值，最好的方式就是沿着梯度寻找。在单方向上，我们可以理解为向着导数大于0的方向寻找，导数大于0，说明此点的方向是上升，再把当前的w加上导数，是不是一种正反馈，很快就可以逼近最大值，当然这只是最简单的理解，实际肯定比这个要复杂滴。
我们再看一个公式：

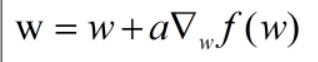
每一次的迭代就是一次权重的更新，新权重是等于原权重加上学习率与梯度的乘积，这里顺带提一下学习率，开始学习率可以大一点，快速逼近最大值，后面就得小，防止在最大值两边徘徊。
撸代码！撸代码！！

import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn import datasets

#第一步得到样本
def get_data():
    digits = datasets.load_digits()
    x, y = digits.data, digits.target
    x = StandardScaler().fit_transform(x)#64
    y = (y > 4).astype(np.int)  # 将大于4和小于4的数字分两组并二值化
    #print(len(y))  1797
    return x,y

def sigmoid(x):
    return 1.0/(1+np.exp(-x))

def logistic():
    data,label = get_data()
    data = np.mat(data) #(1797,64)
    label = np.mat(label).transpose()  #(1797,1)
    m,n = np.shape(data)
    #初次定义权重
    weights = np.ones((n,1))
    #初次定义学习率
    learning_rate = 0.001
    #定义训练轮数
    epoch = 500
    #开始学习
    for i in range(epoch):
        e = sigmoid(data * weights)  #(1797,64) * (64,1) = (1797,1)
        error = (label - e)    #(1797,1)
        weights = weights + learning_rate * data.transpose() * error
    return weights.shape


if __name__ == "__main__":
    print(logistic())  #(64, 1)

从上面代码可以看出，运算量是很大的，每次更新权重都用上了所有的样本，运算复杂，针对这个问题，给大家介绍随机梯度上升法。

2.随机梯度上升法
这个方法最大特点是一次只利用一个样本来更新参数，是一个在线学习算法。
干代码，通过代码来比较！！

import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn import datasets

#第一步得到样本
def get_data():
    digits = datasets.load_digits()
    x, y = digits.data, digits.target
    x = StandardScaler().fit_transform(x)#64
    y = (y > 4).astype(np.int)  # 将大于4和小于4的数字分两组并二值化
    #print(len(y))  1797
    return x,y

def sigmoid(x):
    return 1.0/(1+np.exp(-x))

def logistic2():
    data, label = get_data()
    m,n = data.shape
    # 初次定义权重
    weights = np.ones(n)
    # 初次定义学习率
    learning_rate = 0.001
    for i in range(m):
        e = sigmoid(sum(data[i] * weights))
        error = label[i] - e
        weights = weights + learning_rate * data[i] * error
    return weights

if __name__ == "__main__":
    print(logistic2())  

3.随机梯度下降升级版

import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn import datasets

#第一步得到样本
def get_data():
    digits = datasets.load_digits()
    x, y = digits.data, digits.target
    x = StandardScaler().fit_transform(x)#64
    y = (y > 4).astype(np.int)  # 将大于4和小于4的数字分两组并二值化
    #print(len(y))  1797
    return x,y

def sigmoid(x):
    return 1.0/(1+np.exp(-x))

def logistic3():
    data, label = get_data()
    m,n = data.shape
    # 初次定义权重
    weights = np.ones(n)
    #迭代次数
    epoch = 500
    for i in range(epoch):
        data1 = data
        for j in range(m):
            learning_rate = 4/(1+i+j)+0.001  #学习率不断在变化，但是不会为0
            rand = int(np.random.uniform(0,len(data1))) #随机训练
            e = sigmoid(sum(data1[rand] * weights)) 
            error = label[rand] - e
            weights = weights + learning_rate * data1[rand] * error
            data1 = np.delete(data1, rand,axis = 0)#每次训练完，删除训练的样本
    return weights


if __name__ == "__main__":
    print(logistic3())

升级版的代码优化主要在两个方面，一个是进行学习率的更新，随着学习次数的增加，学习率越来越小，但是不会为0，另一个是进行随机训练，每次样本都是随机抽取，减少周期性波动。

4.终极版（利用sklearn）

import numpy as np
from sklearn.linear_model import LogisticRegression  # 用现成的库进行对比试验
from sklearn.preprocessing import StandardScaler
from sklearn import datasets

#第一步得到样本
def get_data():
    digits = datasets.load_digits()
    x, y = digits.data, digits.target
    x = StandardScaler().fit_transform(x)#64
    y = (y > 4).astype(np.int)  # 将大于4和小于4的数字分两组并二值化
    #print(len(y))  1797
    return x,y


def logistic4():
    data, label = get_data()
    LR = LogisticRegression(C=0.1, penalty='l2', tol=0.001)
    LR.fit(data, label)
    predict = LR.predict(data)
    print((predict == label).astype(np.int).mean())


if __name__ == "__main__":
    logistic4()

LogisticRegression - 参数说明
penalty：惩罚项，str类型，，可选参数为l1和l2，默认为l2。用于指定惩罚项中使用的规范。newton-cg、sag和lbfgs求解算法只支持L2规范。L1G规范假设的是模型的参数满足拉普拉斯分布，L2假设的模型参数满足高斯分布。
tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。
c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。越小的数值表示越强的正则化。