【论文泛读02】大数据交通流预测：一种深度学习方法（SAE模型）

贴一下汇总贴：论文阅读记录

论文链接：《Traffic Flow Prediction With Big Data:A Deep Learning Approach》

一、摘要

准确、及时的交通流信息对智能交通系统的成功部署至关重要。在过去的几年里，交通数据呈爆炸式增长，我们真正进入了交通大数据时代。现有的交通流预测方法主要采用浅层交通预测模型，在许多实际应用中仍不满足要求。这一情况促使我们重新思考基于大交通数据的深度架构模型的交通流预测问题。本文提出了一种基于深度学习的交通流预测方法，该方法考虑了交通流的时空相关性。一种堆叠的自动编码器模型用于学习通用的交通流特征，并以一种贪婪的分层方式进行训练。据我们所知，这是第一次使用自动编码器作为构建块应用深度架构模型来表示用于预测的交通流特征。实验结果表明，所提出的交通流预测方法具有较好的预测性能。

文章主要内容

使用深度学习架构，嵌入Stacked AutoEncoder（SAE）堆叠自编码器作为主体网络结构块来预测交通流。

深度学习的优势：深度学习算法利用多层或深度神经网络体系结构，从最低层次到最高层次逐渐提取数据的固有特征，能够发现数据中大量的内在结构特征。

二、结论

基于SAE模型的深度学习方法用于交通流预测，与以往只考虑交通数据浅层结构的方法不同，该方法能够成功地从交通数据中发现潜在的交通流特征表示，如非线性时空相关性。

采用贪婪分层无监督学习算法对深度网络进行预训练，然后对模型参数进行微调，以提高模型的预测性能。在PeMS数据集上评价了该方法的性能，并与BP神经网络、RW模型、支持向量机模型和RBF神经网络模型进行了比较，结果表明该方法优于其他竞争方法。

可能的研究方向：

• 将这些算法应用于不同的公共开放交通数据集，以检验它们的有效性；
• 这篇文章的预测层只是一个逻辑回归，可以将其扩展到更强大的预测器以进一步提高性能。

三、短期交通流预测的相关研究

• 参数技术：时间序列模型、卡尔曼滤波模型等；
• 非参数方法：k-近邻(k-NN)方法、人工神经网络(ANN)等；
• 模拟方法：使用交通模拟工具来预测交通流量。

四、SAE模型

Stacked Autoencoder（SAE）模型是一个由多层稀疏自编码器组成的深度神经网络模型，其前一层自编码器的输出作为其后一层自编码器的输入，最后一层是个分类器（logistic分类器或者softmax分类器）。

（一）sparse autoencoder算法

sparse autoencoder是一种非监督学习算法，需要满足以下两种约束

• autoencoder：输入等于输出$$h_{W,b}(x)\approx x$$
• sparse：隐层的每个神经元的响应是稀疏的，也就是大部分时间响应为0，也就是平均响应${\hat{p}}_j$尽可能小（其中m为训练样本个数）$${\hat{p}}_j=\frac{1}{m}\sum _{i=1}^m[a_j^{(2)}(x^{(i)})]$$

代价函数

$$J(W,b)=\left[\frac{1}{m}\sum _{i=1}^m\right(\frac{1}{2}||h_{W,b}(x^{(i)})-y^{(i)}|{|}^2)]+\frac{\lambda }{2}\sum _{l=1}^{n_l-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_l+1}(W_{ji}^{(l)}{)}^2+\beta \sum _{j=1}^{s_2}KL(p||{\hat{p}}_j)$$其中$y^{(i)}=x^{(i)}$

• 第一项为autoencoder的约束项；
• 第二项为惩罚项目，防止过拟合；
• 第三项为稀疏的约束，是一个KL散度的衡量标准：$$KL(p||{\hat{p}}_j)=p\log \frac{p}{{\hat{p}}_j}+(1-p)\log \frac{1-p}{1-{\hat{p}}_j}$$

最优化方案

该约束函数是一个非凸函数，采用批量梯度下降算法
$$\begin{gathered} W_{ij}^{(l)}=W_{ij}^{(l)}-\alpha \frac{\partial }{\partial W_{ij}^{(l)}}J(W,b) \\ {b}_i^{(l)}=b_i^{(l)}-\alpha \frac{\partial }{\partial b_i^{(l)}}J(W,b) \end{gathered}$$
其中$$\begin{gathered} \frac{\partial }{\partial W_{ij}^{(l)}}J(W,b)=[\frac{1}{m}\sum _{i=1}^m\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b;x^{(i)},y^{(i)})]+\lambda W_{ij}^{(l)} \\ \frac{\partial }{\partial b_i^{(l)}}J(W,b)=\frac{1}{m}\sum _{i=1}^m\frac{\partial }{\partial b_i^{(l)}}J(W,b;x^{(i)},y^{(i)}) \end{gathered}$$

至于梯度可以用backpropagation（BP）算法来求解；

（二）logistic回归模型与softmax回归模型

logistic回归模型

• 适用于二分类；
• 模型函数：$$h_{\theta }(x)=\frac{1}{1+\exp (-{\theta }^{T}x)}$$
• 代价函数（最大似然）：$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]$$
• 最优化方案：梯度下降算法。

softmax回归模型

• 适用于多分类；
• 模型函数：$$h_{\theta }(x^{(i)})=\left[\begin{array}{c}p(y^{(i)}=1|x^{(i)};\theta )\\ p(y^{(i)}=2|x^{(i)};\theta )\\ ⋮\\ p(y^{(i)}=k|x^{(i)};\theta )\end{array}\right]=\frac{1}{{\sum }_{j=1}^k{e}^{{\theta }_j^T{x}^{(i)}}}\left[\begin{array}{c}{e}^{{\theta }_1^T{x}^{(i)}}\\ e^{{\theta }_2^T{x}^{(i)}}\\ ⋮\\ e^{{\theta }_k^T{x}^{(i)}}\end{array}\right]$$
• 代价函数：$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m\sum _{j=1}^{k}1\{y^{(i)}=j\}\log \frac{e^{{\theta }_j^T{x}^{(i)}}}{{\sum }_{l=1}^k{e}^{{\theta }_l^T{x}^{(i)}}}]+\frac{\lambda }{2}\sum _{i=1}^k\sum _{j=0}^n{\theta }_{ij}^2$$
• 最优化方案：梯度下降算法。

softmax回归分类器适用于k个互斥的类别的分类；k个logistic回归分类器适用k个并不完全互斥的类别的分类。

（三）SAE模型

• 预训练：利用无标签数据对每一层的参数用sparse autoencoder训练初始化；
• 微调：利用有标签数据对整个深度神经网络进行微调。

本文中的应用

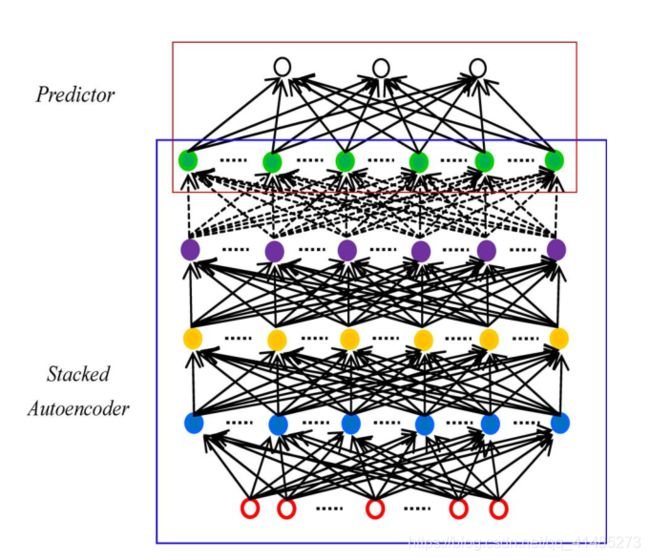
下图便是这篇文章中使用的交通流预测的深度架构模型。采用SAE模型提取交通流特征，采用logistic回归层进行预测。

基于梯度优化技术的BP方法训练深度网络是很简单的。不幸的是，众所周知，用这种方式训练的深度网络性能很差。所以本文采用贪婪分层无监督学习算法的关键是采用自底向上的方式逐层对深层网络进行预训练。在预训练阶段结束后，可以使用BP进行微调，从上至下对模型参数进行微调，同时得到更好的结果。

贪婪分层无监督学习算法：

• 训练第一层作为一个自动编码器通过最小化目标函数与训练集作为输入。
• 将第二层训练成自动编码器，将第一层的输出作为输入。
• 按照第二步中的方法迭代所需的层数。
• 使用最后一层的输出作为预测层的输入，随机或监督训练初始化其参数。
• 在监督的方式下，用BP方法微调所有层的参数。