吴恩达--深度学习笔记
这是一个督促自己学习的笔记
文章目录
-
- 这是一个督促自己学习的笔记
-
- 1.logistic回归
-
- 1. 神经网络基础----二分分类
- 2. logistic回归
- 3. logistic回归损失函数
- 4. 梯度下降法
- 5.logistic回归中的梯度下降法
- 6.m个样本的梯度下降
- 7.向量化
- 8.更多向量化的例子
- 9.向量化logistic回归
- 10.向量化logistic回归的输出
- 11.Python中的广播
- 12.关于python_numpy向量的说明
- 12.logistic损失函数的解释(选修)
- 13.编程作业-----识别猫图
- 2.浅层神经网络
-
- 1.神经网络概览
- 2.神经网络表示
- 3.计算神经网络的输出
- 4.多个例子中的向量化
- 5.向量化实现的解释
- 6.激活函数
- 7.为什么需要非线性激活函数?
- 8.激活函数的导数
- 8.5. 神经网络符号表示(过渡)
- 9.神经网络的梯度下降法
- 10.直观理解反向传播
- 11.随机初始化
- 3.深度神经网络
-
- 1.深层神经网络
- 2.深层网络中的正向传播
- 3.核对矩阵的维数
- 4.为什么使用深层表示
- 5.搭建深层网络块
- 6.前向和反向传播
- 7.参数与超参数
- 8.这和大脑有什么关系?
- 9.搭建一个多隐藏层的神经网络代码实现
1.logistic回归
1. 神经网络基础----二分分类
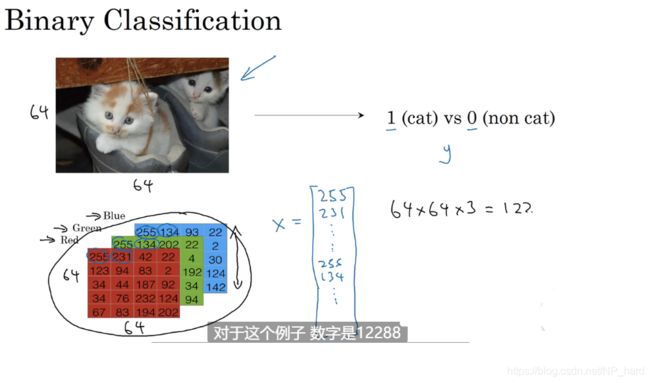
把一张含有猫的图片作为输入,要求输出1 or 0
首先,猫的图片可以分为三个图层,红,绿,蓝,三个图层分别从上往下,从左往右读取灰度值,构成一个列向量Xi(Mx1),假设训练集有N张照片,则这N张照片可以合成一个矩阵(MxN),可以通过python的x.shape得到矩阵的大小。
2. logistic回归
从上文得知x为为一列向量,代表着一张图片,通过线性回归函数
y ^ = w T x + b \hat{y}= w^{T}x+b y^=wTx+b可以预测出y的值,可是这种方式预测出的y的范围非常广,而我们想要的是y处于0-1之间,表示x这张图片是猫的概率,因此引入sigmoid函数通过 y ^ = σ ( w T x + b ) \hat{y}= \sigma(w^{T}x+b) y^=σ(wTx+b)使得y分布再0-1之间,如下图所示。
3. logistic回归损失函数

好了,我们现在有一组猫的图片,即一个MxN的矩阵,这作为训练集,通过线性回归函数和sigmoid函数,我们可以输入一张图片然后通过函数的作用映射为图片是猫图的概率y了,那么,我们该如何训练出参数w和b呢?
我们应该定义一个loss函数,描述预测值 y ^ \hat{y} y^和y之间的差值了。
我们可以定义loss函数为 L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 L(\hat{y},y)=\frac{1}{2}(\hat{y}-y)^{2} L(y^,y)=21(y^−y)2
但是这样可能会产生多个凹凸区间,无法得到最优解。
于是我们打算使用 L ( y ^ , y ) = − ( y l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ ) ) L(\hat{y},y)=-(ylog(\hat{y})+(1-y)log(1-\hat{y})) L(y^,y)=−(ylog(y^)+(1−y)log(1−y^))
这个函数是有全局最优解的
当 y=0时 L ( y ^ , y ) = − l o g ( 1 − y ^ ) L(\hat{y},y)=-log(1-\hat{y}) L(y^,y)=−log(1−y^)
因为我们希望loss函数尽可能小
则我们希望 y ^ \hat{y} y^尽可能小。
反之,当y=1时
L ( y ^ , y ) = − l o g ( y ^ ) L(\hat{y},y)=-log(\hat{y}) L(y^,y)=−log(y^)因为我们希望loss函数尽可能的小,所以我们希望 y ^ \hat{y} y^尽可能大
于是当我们的预测值越接近实际值时,loss函数就越小,这就是loss函数的目的。
最后的全局平均花费函数
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)}) J(w,b)=m1i=1∑mL(y^(i),y(i))
4. 梯度下降法
我们现在有了全局平均花费函数 J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)}) J(w,b)=m1i=1∑mL(y^(i),y(i))
可以看出,全局损失函数是关于w和b的函数,要想求得最小值,必须调整参数w和b
问题是,我们如何找到这个函数的全局最优解呢?(即最小值)
我们将采取梯度下降法来求解
而所谓的梯度下降法,就是令J(w,b)函数分别对w和b求偏导得到斜率,再分别将w和b的斜率乘以一定的学习率得到参数w和b需要移动的大小,然后移动w和b,由于J(w,b)是一个凸优化函数,故我们最后一定能让w和b移动到全局最优解的位置,使得全局损失值最小,函数拟合的最好

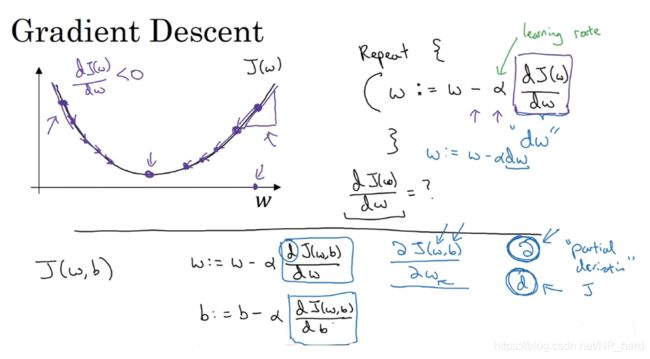
如何进行梯度下降呢?其实梯度下降就是任意找个点为初始点(一般来说会选择坐标原点),不断进行移动,直至到达最优解点
通过下列公式
ω : = ω − α ∂ J ( ω , b ) ∂ ω \omega:=\omega-\alpha\frac{\partial J(\omega,b)}{\partial \omega} ω:=ω−α∂ω∂J(ω,b)
b : = b − α ∂ J ( ω , b ) ∂ b b:=b-\alpha\frac{\partial J(\omega,b)}{\partial b} b:=b−α∂b∂J(ω,b)
5.logistic回归中的梯度下降法
holy shit,笔记写到一半忘了保存了
好的,我们现在准备输入五个参数,分别是x1,x2,w1,w2,b,通过线性回归公式,sigmoid函数,最终得到loss函数的loss值。你懂的,我们一开始并不知道参数w1,w2,b的值,所以才要通过梯度下降公式对这三个参数进行缓慢调整,那么如何调整呢?

由上图可以看出,梯度下降的幅度是从后往前计算的
d a = d L ( a , y ) d a , d z = d L ( a , y ) d z = d L d a d a d z da=\frac{dL(a,y)}{da},dz=\frac{dL(a,y)}{dz}=\frac{dL}{da}\frac{da}{dz} da=dadL(a,y),dz=dzdL(a,y)=dadLdzda
所以 d w 1 = d L d w 1 = x 1 d z dw_{1}=\frac{dL}{dw_{1}}=x_{1}dz dw1=dw1dL=x1dz
d w 2 = d L d w 2 = x 2 d z dw_{2}=\frac{dL}{dw_{2}}=x_{2}dz dw2=dw2dL=x2dz
d b = d L d b = d z db=\frac{dL}{db}=dz db=dbdL=dz
最终
w 1 : = w 1 − α d w 1 w_{1}:=w_{1}-\alpha dw_{1} w1:=w1−αdw1
w 2 : = w 2 − α d w 2 w_{2}:=w_{2}-\alpha dw_{2} w2:=w2−αdw2
b : = b − α d z b:=b-\alpha dz b:=b−αdz
完成一次梯度下降
6.m个样本的梯度下降
7.向量化

所以究竟什么是向量化?对于这样一个矩阵方程
z = w T x + b z=w^{T}x+b z=wTx+b
其中
w = [ ⋮ ⋮ ⋮ ] , x = [ ⋮ ⋮ ⋮ ] w=\begin{bmatrix} \vdots\\ \vdots \\ \vdots\\ \end{bmatrix},x=\begin{bmatrix} \vdots\\ \vdots \\ \vdots\\ \end{bmatrix} w=⎣⎢⎢⎢⎡⋮⋮⋮⎦⎥⎥⎥⎤,x=⎣⎢⎢⎢⎡⋮⋮⋮⎦⎥⎥⎥⎤
计算两个矩阵相乘的结果有两种方法
1.for循环
2.向量相乘
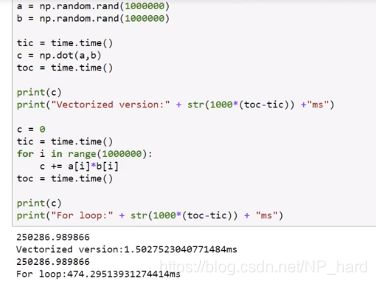
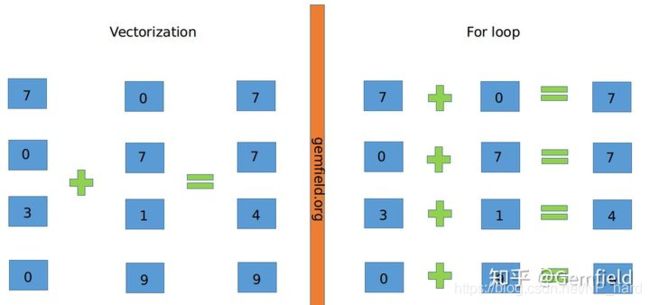
由上图可见两者效率相差有将近300倍
那么,为什么向量化计算会这么快呢?
什么是vectorization?
向量化计算(vectorization),也叫vectorized operation,也叫array programming,说的是一个事情:将多次for循环计算变成一次计算
上图中,左侧为vectorization,右侧为寻常的For loop计算。将多次for循环计算变成一次计算完全仰仗于CPU的SIMD指令集,SIMD指令可以在一条cpu指令上处理2、4、8或者更多份的数据。在Intel处理器上,这个称之为SSE以及后来的AVX,在Arm处理上,这个称之为NEON。
因此简单来说,向量化计算就是将一个loop——处理一个array的时候每次处理1个数据共处理N次,转化为vectorization——处理一个array的时候每次同时处理8个数据共处理N/8次。
引用链接
8.更多向量化的例子
上一小节我们明白了什么是向量化,这一小节我们来看看更多向量化的例子
1.假设u为矩阵A和向量v的乘积,显然,矩阵的计算公式为
u = ∑ i ∑ j A i j v j u=\sum_{i}\sum_{j}A_{ij}v_{j} u=i∑j∑Aijvj

我们当然可以将这种耗时的for loop计算转化为右图的向量化计算
2.对向量中的每一个元素进行诸如指数运算,幂指运算,取逆运算等操作时,numpy库也有提供 内置函数,运算要比我们进行for loop要快

3.下面为logistic回归的逻辑流程,我们看看哪里可以进行向量化优化
(注意:这只是对一个样本进行梯度下降运算)

可优化的位置如下图所示,在计算dw1,dw2处时,如果你的线性回归方程的特征值不止两个,那么这里就会有个for loop,我们在这里可以进行向量化

9.向量化logistic回归
好了,我们在上一节中学习了如何对一个样本进行向量化,但是在logistic回归中,样本集有m个样本,我们要对这m个样本进行梯度下降处理,这样不可避免地需要用到for-loop,那么,对m个样本的操作也可以进行向量化吗?

如上图所示,对于每一个样本,我们都进行第一个红框的运算,即先进行线性回归运算,再进行sigmoid运算,注意到,在前几节中,我们用一个nxm的矩阵表示整个样本集,即
X = [ ⋮ ⋮ ⋮ ⋮ x ( 1 ) x ( 2 ) ⋯ x ( m ) ⋮ ⋮ ⋮ ⋮ ] X=\begin{bmatrix} \vdots&\vdots&\vdots&\vdots\\ x^{(1)}&x^{(2)}&\cdots&x^{(m)}\\ \vdots&\vdots&\vdots&\vdots\\ \end{bmatrix} X=⎣⎢⎢⎡⋮x(1)⋮⋮x(2)⋮⋮⋯⋮⋮x(m)⋮⎦⎥⎥⎤
故样本集的回归方程可表示为:
Z = [ z ( 1 ) z ( 2 ) ⋯ z ( m ) ] = w T X + [ b b ⋯ b ] Z=\begin{bmatrix}z^{(1)}&z^{(2)}&\cdots&z^{(m)}\end{bmatrix}=w^{T}X+\begin{bmatrix}b&b&\cdots&b\end{bmatrix} Z=[z(1)z(2)⋯z(m)]=wTX+[bb⋯b]
= [ w T x ( 1 ) + b w T x ( 2 ) + b ⋯ w T x ( m ) + b ] =\begin{bmatrix}w^{T}x^{(1)}+b&w^{T}x^{(2)}+b&\cdots&w^{T}x^{(m)}+b\end{bmatrix} =[wTx(1)+bwTx(2)+b⋯wTx(m)+b]
即Z=np.dot(w.T,x)+b(b自动转化为1xm的矩阵,这是由于python的广播特性)
最后
A = [ a ( 1 ) a ( 2 ) ⋯ a ( m ) ] = σ ( Z ) A=\begin{bmatrix}a^{(1)}&a^{(2)}&\cdots&a^{(m)}\end{bmatrix}=\sigma(Z) A=[a(1)a(2)⋯a(m)]=σ(Z)
10.向量化logistic回归的输出
哇塞,通过以上的优化,我们真的可以得到高度向量化的logistic回归程序!
如下图,db就是所有dz(i)之和的平均值,我们可以用numpy的sum函数来代替for-loop
而dw也可以向量化为简单的矩阵乘法

而对整个样本集的一次梯度回归运算也竟然可以被向量化的如此清爽!
当然,如果你想要经过多次求导来进行梯度下降计算,那不可避免地需要使用for-loop,而这是无法避免的

11.Python中的广播
python中的广播就是一种技巧,例如,当你在python中将一个mxn矩阵加减乘除一个1xn矩阵时,1xn矩阵会自动转化为mxn矩阵,然后两个矩阵对应的元素各自进行运算,对于mx1矩阵同理

12.关于python_numpy向量的说明

嗯。。。吴恩达大佬在这一节中主要讲了一些编程技巧来让你的代码不那么容易出bug
当我们利用numpy创建矩阵或向量时,尽量使用如上图所示的第二种方法,因为第一种方法生成的a会是一个秩为1的array,它的转置和内积都会很奇怪
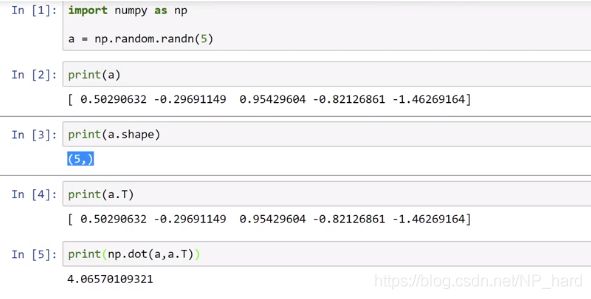
而使用第二种方法创建的a如下图所示
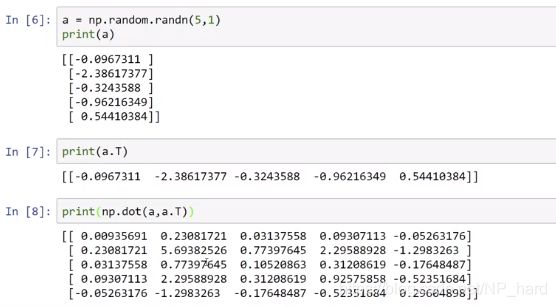
12.logistic损失函数的解释(选修)
你一定很好奇,损失函数 J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)}) J(w,b)=m1i=1∑mL(y^(i),y(i)) L ( y ^ , y ) = − ( y l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ ) ) L(\hat{y},y)=-(ylog(\hat{y})+(1-y)log(1-\hat{y})) L(y^,y)=−(ylog(y^)+(1−y)log(1−y^))是怎么得到的吧?

如上图所示,给定特征值x,y=1的条件概率为y_hat,而给定特征值x,y=0的概率为1-y_hat,我们可以构造一个条件概率函数
p ( y ∣ x ) = y ^ y ( 1 − y ^ ) ( 1 − y ) p(y|x)=\hat{y}^{y}(1-\hat{y})^{(1-y)} p(y∣x)=y^y(1−y^)(1−y)
来满足上面两个式子,又因为log函数是严格单增函数,设计函数
l o g ( p ( y ∣ x ) ) = l o g ( y ^ y ( 1 − y ^ ) ( 1 − y ) ) log(p(y|x))=log(\hat{y}^{y}(1-\hat{y})^{(1-y)}) log(p(y∣x))=log(y^y(1−y^)(1−y))
= y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) = − L ( y , y ^ ) =ylog\hat{y}+(1-y)log(1-\hat{y})=-L(y,\hat{y}) =ylogy^+(1−y)log(1−y^)=−L(y,y^)
可见 L ( y , y ^ ) L(y,\hat{y}) L(y,y^)就是单个样本的损失函数,在logistic回归中,我们想将loss值减到最小,那么就是将log(p(y|x))增到最大
那么如何将log(p(y|x))增到最大呢?这个我们先不谈
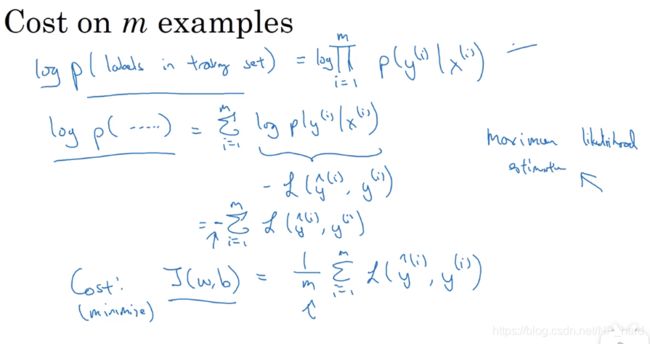
当训练集中有m个样本时,
l o g ( p ( . . . ) ) = − ∑ i = 1 m L ( y ( i ) ^ , y ( i ) ) log(p(...))=-\sum_{i=1}^{m}L(\hat{y^{(i)}},y^{(i)}) log(p(...))=−i=1∑mL(y(i)^,y(i))
其实这里我还没搞懂
而统计学里有一种求最大值的方法为最大似然法,我们可以求出log(p(…))的最大值
又由于 C o s t : J ( w , b ) = 1 m ∑ i = 1 m L ( y ( i ) ^ , y ( i ) ) Cost:J(w,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y^{(i)}},y^{(i)}) Cost:J(w,b)=m1i=1∑mL(y(i)^,y(i))
所以当log函数求得最大值时,Cost即为最小值
13.编程作业-----识别猫图
链接: 识别猫图
2.浅层神经网络
1.神经网络概览
好的,经过上一章的logistic回归的学习,以及识别cat的一个小编程作业,我们明白了神经网络大概应该是什么样子,那么,logistic回归和神经网络究竟有什么区别呢?
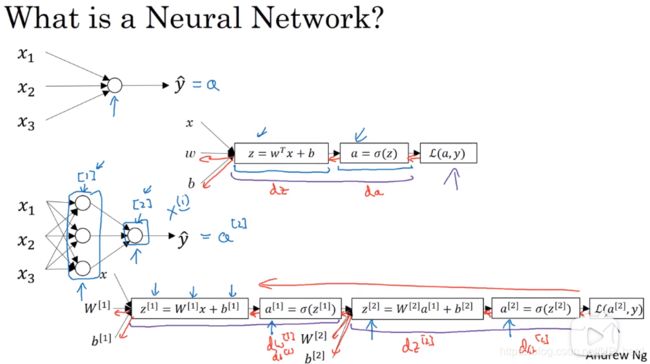
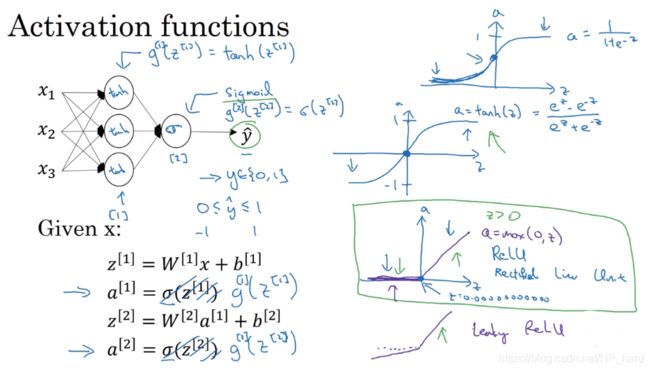
由上图我们可以看出,相比较于logistic回归,神经网络的层数多了,与此同时第一层的节点数也多了,再比较两者的计算流程图,可以发现神经网络多次使用线性回归函数和sigmoid函数来计算z
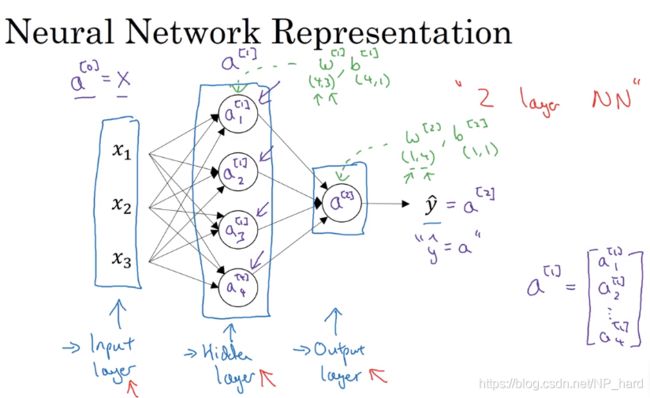
2.神经网络表示
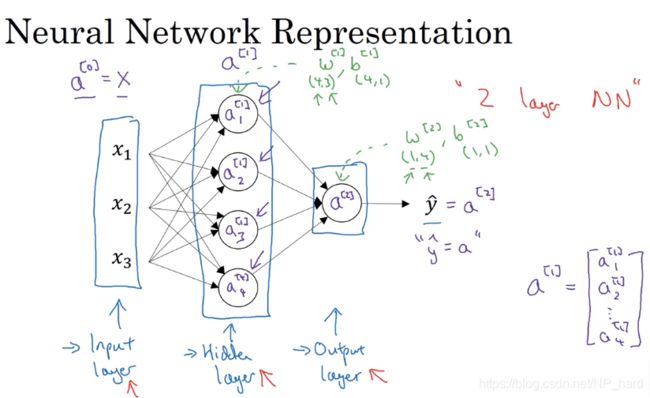
神经网络的表示如上图所示,上图为一个双层神经网络(一般来说人们会将输入层视为第0层,不计入层数),中间的那层为隐藏层,最后一层为输出层
输入层会读入x1,x2,x3,然后将这些值传入隐藏层,通过线性回归函数和sigmoid函数,隐藏层将计算出激活值a^(1),其中
a [ 1 ] = [ a 1 [ 1 ] a 2 [ 2 ] ⋮ a 4 [ 4 ] ] a^{[1]}=\begin{bmatrix} a_{1}^{[1]}\\ a_{2}^{[2]}\\ \vdots\\ a_{4}^{[4]} \end{bmatrix} a[1]=⎣⎢⎢⎢⎢⎡a1[1]a2[2]⋮a4[4]⎦⎥⎥⎥⎥⎤
将a^ (1)作为参数输入输出层,同样经过计算,输出层得出a^(2),a ^(2)即为y_hat
3.计算神经网络的输出
如下图所示,将神经网络中的单个神经元拿出来,其计算过程与logistic回归并无不同,同样是经过线性回归方程和sigmoid函数计算得出激活值y_hat,右图为两个例子
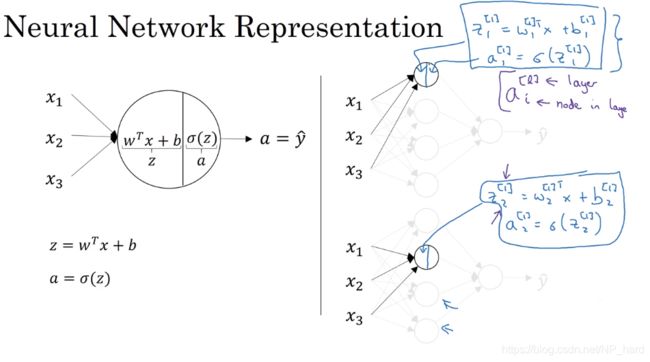
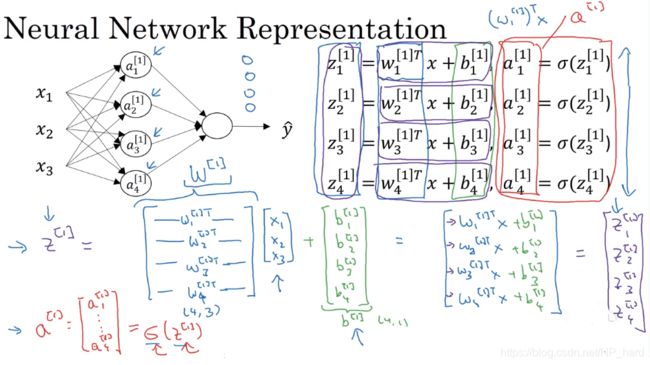
那么好了,我们现在要计算第一层的激活值,即 a 1 [ 1 ] , a 2 [ 1 ] , a 3 [ 1 ] , a 4 [ 1 ] a_{1}^{[1]},a_{2}^{[1]},a_{3}^{[1]},a_{4}^{[1]} a1[1],a2[1],a3[1],a4[1]
我们肯定不能使用低效的for-loop,我们试着看能不能将这一系列的计算向量化,于是我们有了下列等式
z [ 1 ] = [ ⋯ w 1 [ 1 ] T ⋯ ⋯ w 2 [ 1 ] T ⋯ ⋯ w 3 [ 1 ] T ⋯ ⋯ w 4 [ 1 ] T ⋯ ] [ x 1 x 2 x 3 ] + [ b 1 [ 1 ] b 2 [ 1 ] b 3 [ 1 ] b 4 [ 1 ] ] = [ w 1 [ 1 ] T x + b 1 [ 1 ] w 2 [ 1 ] T x + b 2 [ 1 ] w 3 [ 1 ] T x + b 3 [ 1 ] w 4 [ 1 ] T x + b 4 [ 1 ] ] = [ z 1 [ 1 ] z 2 [ 1 ] z 3 [ 1 ] z 4 [ 1 ] ] z^{[1]}= \begin{bmatrix} \cdots&w_{1}^{[1]T}\cdots\\ \cdots&w_{2}^{[1]T}\cdots\\ \cdots&w_{3}^{[1]T}\cdots\\ \cdots&w_{4}^{[1]T}\cdots\\ \end{bmatrix} \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ \end{bmatrix}+ \begin{bmatrix} b_{1}^{[1]}\\ b_{2}^{[1]}\\ b_{3}^{[1]}\\ b_{4}^{[1]}\\ \end{bmatrix}= \begin{bmatrix} w_{1}^{[1]T}x+b_{1}^{[1]}\\ w_{2}^{[1]T}x+b_{2}^{[1]}\\ w_{3}^{[1]T}x+b_{3}^{[1]}\\ w_{4}^{[1]T}x+b_{4}^{[1]}\\ \end{bmatrix}= \begin{bmatrix} z_{1}^{[1]}\\ z_{2}^{[1]}\\ z_{3}^{[1]}\\ z_{4}^{[1]}\\ \end{bmatrix} z[1]=⎣⎢⎢⎢⎡⋯⋯⋯⋯w1[1]T⋯w2[1]T⋯w3[1]T⋯w4[1]T⋯⎦⎥⎥⎥⎤⎣⎡x1x2x3⎦⎤+⎣⎢⎢⎢⎡b1[1]b2[1]b3[1]b4[1]⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡w1[1]Tx+b1[1]w2[1]Tx+b2[1]w3[1]Tx+b3[1]w4[1]Tx+b4[1]⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡z1[1]z2[1]z3[1]z4[1]⎦⎥⎥⎥⎤
然后计算a[1]
a [ 1 ] = [ a 1 [ 1 ] a 2 [ 1 ] a 3 [ 1 ] a 4 [ 1 ] ] = σ ( z [ 1 ] ) a^{[1]}=\begin{bmatrix} a_{1}^{[1]}\\ a_{2}^{[1]}\\ a_{3}^{[1]}\\ a_{4}^{[1]}\\ \end{bmatrix}=\sigma(z^{[1]}) a[1]=⎣⎢⎢⎢⎡a1[1]a2[1]a3[1]a4[1]⎦⎥⎥⎥⎤=σ(z[1])
于是我们就计算出了第一层的激活值啦!!
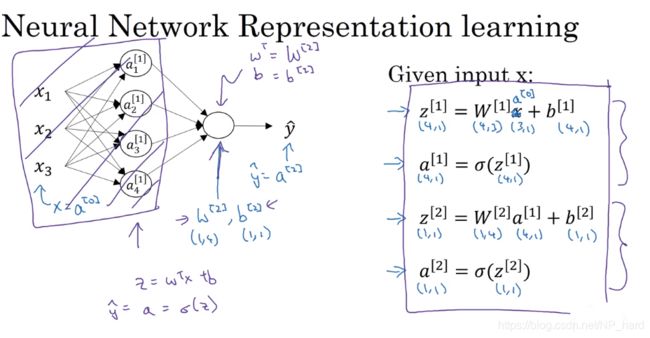
整个流程可以总结为上面四个式子
4.多个例子中的向量化
holy shit,笔记又忘记保存了
好的,收拾一下心情,在上一小结中,我们学习了使用一个样本来训练神经网络并向量化,在这一小节中,我们需要学习对于含有m个样本的样本集,我们如何向量化以代替遍历样本集

首先我们得设定一些助记符
X ⇒ a [ 2 ] = y ^ X\Rightarrow a^{[2]}=\hat{y} X⇒a[2]=y^
x ( 1 ) ⇒ a [ 2 ] ( 1 ) = y ^ ( 1 ) x^{(1)}\Rightarrow a^{[2](1)}=\hat{y}^{(1)} x(1)⇒a[2](1)=y^(1)
x ( 2 ) ⇒ a [ 2 ] ( 2 ) = y ^ ( 2 ) x^{(2)}\Rightarrow a^{[2](2)}=\hat{y}^{(2)} x(2)⇒a[2](2)=y^(2)
⋮ \vdots ⋮
x ( m ) ⇒ a [ 2 ] ( m ) = y ^ ( m ) x^{(m)}\Rightarrow a^{[2](m)}=\hat{y}^{(m)} x(m)⇒a[2](m)=y^(m)
x(i)代表第i个样本的特征向量,y_hat(i)表示第i个样本的第一层激发值

故整个流程(样本集)如上图红框所示,上图中,X矩阵表示样本集,A[1]矩阵表示样本集中每一个样本的第一层的激发向量,例如,A[1]的左上角为第一个样本的第一层的最上面的节点的激发值
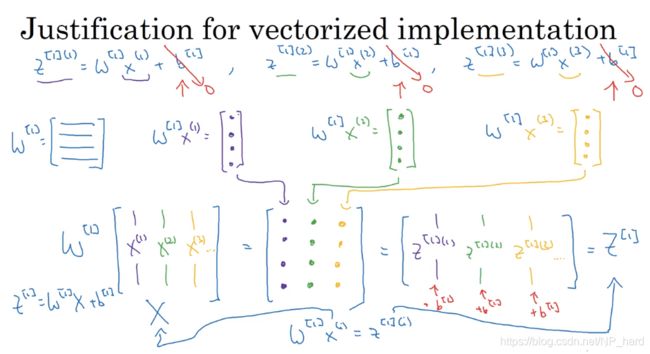
5.向量化实现的解释
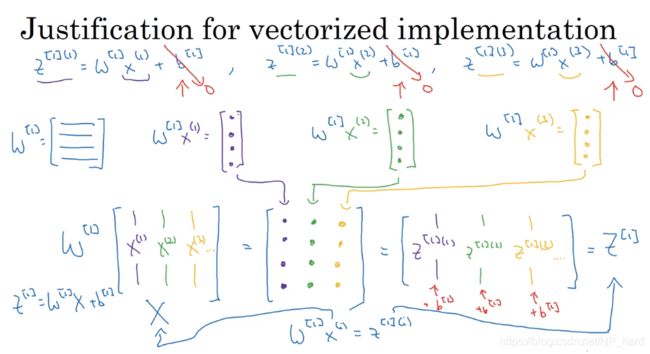
为了简便,我们将b设为0
我们明白,对于一个样本x(1),W[1]x(1)就等于一个列向量z[1] (1),即第一层的待激活值,如此,我们可以将样本x(i)堆叠起来形成矩阵X(样本集)
W [ 1 ] = [ ⋯ w 1 [ 1 ] T ⋯ ⋯ w 2 [ 1 ] T ⋯ ⋯ w 3 [ 1 ] T ⋯ ⋯ w 4 [ 1 ] T ⋯ ] W^{[1]}=\begin{bmatrix} \cdots&w_{1}^{[1]T}\cdots\\ \cdots&w_{2}^{[1]T}\cdots\\ \cdots&w_{3}^{[1]T}\cdots\\ \cdots&w_{4}^{[1]T}\cdots\\ \end{bmatrix} W[1]=⎣⎢⎢⎢⎡⋯⋯⋯⋯w1[1]T⋯w2[1]T⋯w3[1]T⋯w4[1]T⋯⎦⎥⎥⎥⎤
那么就有 Z [ 1 ] = W [ 1 ] X + b [ 1 ] Z^{[1]}=W^{[1]}X+b^{[1]} Z[1]=W[1]X+b[1]
以此类推,就有
A [ 1 ] = σ ( Z [ 1 ] ) A^{[1]}=\sigma(Z^{[1]}) A[1]=σ(Z[1])
Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]} Z[2]=W[2]A[1]+b[2]
A [ 2 ] = σ ( Z [ 2 ] ) A^{[2]}=\sigma(Z^{[2]}) A[2]=σ(Z[2])
总流程如下图

至此,我们完成了样本集训练神经网络的向量化
6.激活函数
激活函数主要分为下列四种
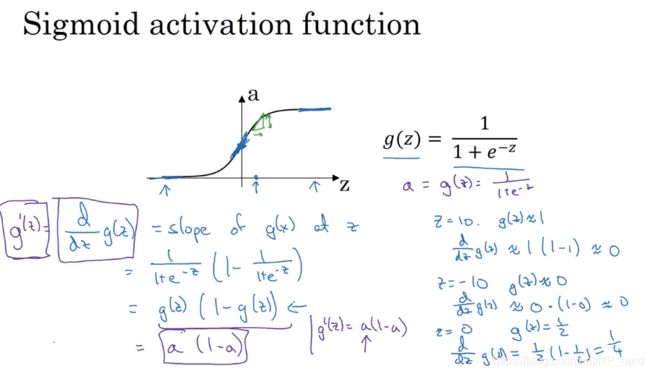
s i g m o i d : a = 1 1 + e − z sigmoid: a=\frac{1}{1+e^{-z}} sigmoid:a=1+e−z1
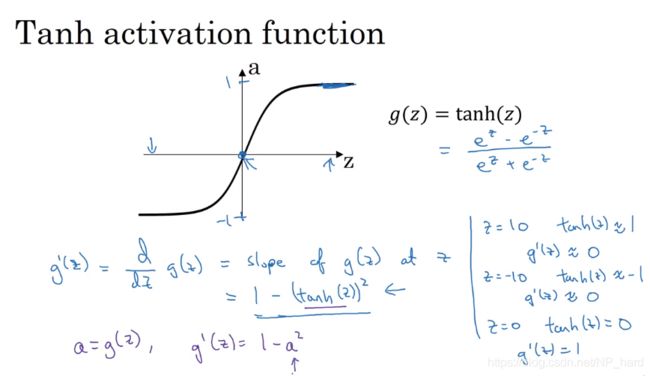
t a n h : a = e z − e − z e z + e − z tanh: a=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} tanh:a=ez+e−zez−e−z
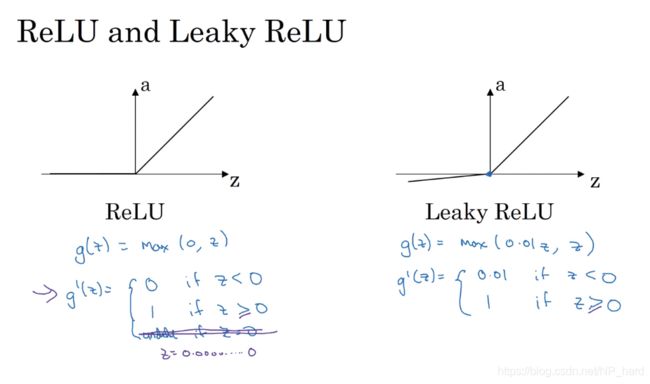
R e l u : a = m a x ( 0 , z ) Relu: a=max(0,z) Relu:a=max(0,z)
l e a k y R e l u : a = m a x ( 0.01 ∗ z , z ) leaky Relu: a=max(0.01*z,z) leakyRelu:a=max(0.01∗z,z)
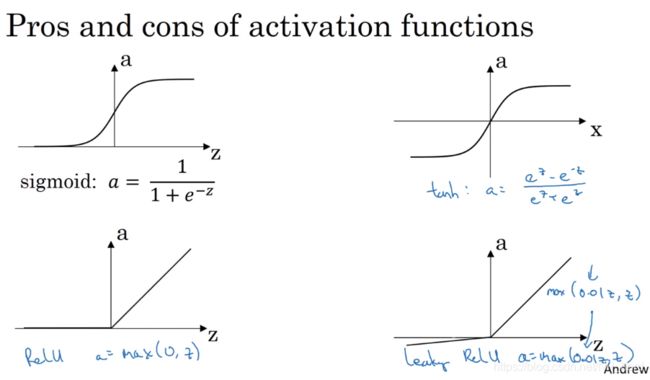
对于sigmoid和tanh这两个激活函数,一般来说很少使用sigmoid函数,只有在二元分类问题的输出层中,为了表示概率[0~1]才使用sigmoid函数,tanh函数就是将sigmoid函数下移,但是tacnh函数在各个方面的性能都好于sigmoid函数
但是由于tanh函数在x很大的时候,图像趋于平缓,导数很小,梯度下降的速度很慢,所以人们现在一般都使用Relu函数(rectified linear unit 修正线性单元),这个函数在z大于0的情况下导数恒为1,梯度下降的速度恒定,但是z小于0的时候导数为0,不能进行梯度下降,但是在实际应用中,有足够多的隐藏单元可以使得z大于0,所以不用担心,对于Relu函数,其原点处导数不存在,由于出现在原点处的概率(00000000)很低,所以不用考虑,你也可以将原点处的导数初始化为1或者0
有些学者为了解决z小于0的情况,发明了linky Relu函数,即a=max(0.01*z,z),当z小于0,其导数为0.01
7.为什么需要非线性激活函数?

为什么我们需要非线性激活函数?如果使用线性激活函数会怎么样?
先给出结论
如果使用线性激活函数,那么所有的隐藏层都是无用的
简单证明:
i f , a [ 1 ] = z [ 1 ] = w [ 1 ] x + b [ 1 ] if ,a^{[1]}=z^{[1]}=w^{[1]}x+b^{[1]} if,a[1]=z[1]=w[1]x+b[1]
a [ 2 ] = z [ 2 ] = w [ 2 ] a [ 1 ] + b [ 2 ] a^{[2]}=z^{[2]}=w^{[2]}a^{[1]}+b^{[2]} a[2]=z[2]=w[2]a[1]+b[2]
t h e n , a [ 2 ] = w [ 2 ] ( w [ 1 ] x + b [ 1 ] ) + b [ 2 ] then,a^{[2]}=w^{[2]}(w^{[1]}x+b^{[1]})+b^{[2]} then,a[2]=w[2](w[1]x+b[1])+b[2]
= ( w [ 2 ] w [ 1 ] ) x + ( w [ 2 ] b [ 1 ] + b [ 2 ] ) =(w^{[2]}w^{[1]})x+(w^{[2]}b^{[1]}+b^{[2]}) =(w[2]w[1])x+(w[2]b[1]+b[2])
= w ′ x + b ′ =w^{'}x+b^{'} =w′x+b′
链接: 为什么要使用非线性激活函数?
8.激活函数的导数
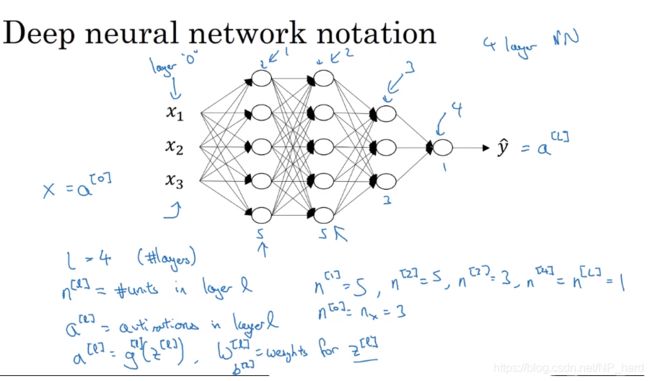
8.5. 神经网络符号表示(过渡)
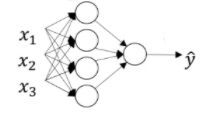
1.nx即为每层的顶点个数
n x = n [ 0 ] , n [ 1 ] , n [ 2 ] n_{x}=n^{[0]},n^{[1]},n^{[2]} nx=n[0],n[1],n[2]
上图有n[0]=3,n[1]=4,n[2]=1
2.a[i]是列向量,表示第i层的激活值
a [ 1 ] = [ a 1 [ 1 ] a 2 [ 1 ] ⋮ a 4 [ 1 ] ] a^{[1]}=\begin{bmatrix} a_{1}^{[1]}\\ a_{2}^{[1]}\\ \vdots\\ a_{4}^{[1]}\\ \end{bmatrix} a[1]=⎣⎢⎢⎢⎢⎡a1[1]a2[1]⋮a4[1]⎦⎥⎥⎥⎥⎤
3.x为列向量,x(i)表示第i个样本的输入,即a[0]
x = [ x 1 x 2 x 3 ] x ( 1 ) = [ x 1 ( 1 ) x 2 ( 1 ) x 3 ( 1 ) ] x=\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3} \end{bmatrix} x^{(1)}=\begin{bmatrix} x_{1}^{(1)}\\ x_{2}^{(1)}\\ x_{3}^{(1)} \end{bmatrix} x=⎣⎡x1x2x3⎦⎤x(1)=⎣⎢⎡x1(1)x2(1)x3(1)⎦⎥⎤
4.X矩阵表示样本集
X = [ ⋮ ⋮ ⋮ ⋮ x ( 1 ) x ( 2 ) ⋯ x ( m ) ⋮ ⋮ ⋮ ⋮ ] X=\begin{bmatrix} \vdots&\vdots&\vdots&\vdots\\ x^{(1)}&x^{(2)}&\cdots&x^{(m)}\\ \vdots&\vdots&\vdots&\vdots\\ \end{bmatrix} X=⎣⎢⎢⎡⋮x(1)⋮⋮x(2)⋮⋮⋯⋮⋮x(m)⋮⎦⎥⎥⎤
5.A[1]矩阵表示样本集中m个样本的第一层的激发向量
A [ 1 ] = [ ⋮ ⋮ ⋮ ⋮ a [ 1 ] ( 1 ) a [ 1 ] ( 2 ) ⋯ a [ 1 ] ( m ) ⋮ ⋮ ⋮ ⋮ ] A^{[1]}=\begin{bmatrix} \vdots&\vdots&\vdots&\vdots\\ a^{[1](1)}&a^{[1](2)}&\cdots&a^{[1](m)}\\ \vdots&\vdots&\vdots&\vdots\\ \end{bmatrix} A[1]=⎣⎢⎢⎡⋮a[1](1)⋮⋮a[1](2)⋮⋮⋯⋮⋮a[1](m)⋮⎦⎥⎥⎤
6.W[i](n[i] x n[i-1])是列向量(矩阵),表示神经网络的第i层的所有w参数
W [ 1 ] = [ ⋯ w 1 [ 1 ] T ⋯ ⋯ w 2 [ 1 ] T ⋯ ⋯ w 3 [ 1 ] T ⋯ ⋯ w 4 [ 1 ] T ⋯ ] W^{[1]}=\begin{bmatrix} \cdots&w_{1}^{[1]T}\cdots\\ \cdots&w_{2}^{[1]T}\cdots\\ \cdots&w_{3}^{[1]T}\cdots\\ \cdots&w_{4}^{[1]T}\cdots\\ \end{bmatrix} W[1]=⎣⎢⎢⎢⎡⋯⋯⋯⋯w1[1]T⋯w2[1]T⋯w3[1]T⋯w4[1]T⋯⎦⎥⎥⎥⎤
例如,W[1](n[1] x n[0])(4x3),W[1]为第一层的w参数矩阵
7.b[i]表示神经网络第i层的所有b参数
b [ 1 ] = [ b 1 [ 1 ] b 2 [ 1 ] b 3 [ 1 ] b 4 [ 1 ] ] b^{[1]}=\begin{bmatrix} b_{1}^{[1]}\\ b_{2}^{[1]}\\ b_{3}^{[1]}\\ b_{4}^{[1]}\\ \end{bmatrix} b[1]=⎣⎢⎢⎢⎡b1[1]b2[1]b3[1]b4[1]⎦⎥⎥⎥⎤
8.Z[i]=W[i]X+b[i],Z[i]矩阵表示样本集中m个样本第i层的线性回归值
Z [ 1 ] ( 1 ) = W [ 1 ] x ( 1 ) + b [ 1 ] , Z [ 1 ] ( 2 ) = W [ 1 ] x ( 2 ) + b [ 1 ] Z^{[1](1)}=W^{[1]}x^{(1)}+b^{[1]},Z^{[1](2)}=W^{[1]}x^{(2)}+b^{[1]} Z[1](1)=W[1]x(1)+b[1],Z[1](2)=W[1]x(2)+b[1]
Z [ 1 ] = W [ 1 ] X + b [ 1 ] Z^{[1]}=W^{[1]}X+b^{[1]} Z[1]=W[1]X+b[1]
= [ ⋯ w 1 [ 1 ] T ⋯ ⋯ w 2 [ 1 ] T ⋯ ⋯ w 3 [ 1 ] T ⋯ ⋯ w 4 [ 1 ] T ⋯ ] [ ⋮ ⋮ ⋮ ⋮ x ( 1 ) x ( 2 ) ⋯ x ( m ) ⋮ ⋮ ⋮ ⋮ ] + b [ 1 ] =\begin{bmatrix} \cdots&w_{1}^{[1]T}\cdots\\ \cdots&w_{2}^{[1]T}\cdots\\ \cdots&w_{3}^{[1]T}\cdots\\ \cdots&w_{4}^{[1]T}\cdots\\ \end{bmatrix} \begin{bmatrix} \vdots&\vdots&\vdots&\vdots\\ x^{(1)}&x^{(2)}&\cdots&x^{(m)}\\ \vdots&\vdots&\vdots&\vdots\\ \end{bmatrix}+b^{[1]} =⎣⎢⎢⎢⎡⋯⋯⋯⋯w1[1]T⋯w2[1]T⋯w3[1]T⋯w4[1]T⋯⎦⎥⎥⎥⎤⎣⎢⎢⎡⋮x(1)⋮⋮x(2)⋮⋮⋯⋮⋮x(m)⋮⎦⎥⎥⎤+b[1]
= [ ⋮ ⋮ ⋮ ⋮ W [ 1 ] x ( 1 ) + b [ 1 ] W [ 1 ] x ( 2 ) + b [ 1 ] ⋯ W [ 1 ] x ( m ) + b [ 1 ] ⋮ ⋮ ⋮ ⋮ ] =\begin{bmatrix} \vdots&\vdots&\vdots&\vdots\\ W^{[1]}x^{(1)}+b^{[1]}&W^{[1]}x^{(2)}+b^{[1]}&\cdots&W^{[1]}x^{(m)}+b^{[1]}\\ \vdots&\vdots&\vdots&\vdots \end{bmatrix} =⎣⎢⎢⎡⋮W[1]x(1)+b[1]⋮⋮W[1]x(2)+b[1]⋮⋮⋯⋮⋮W[1]x(m)+b[1]⋮⎦⎥⎥⎤
= [ ⋮ ⋮ ⋮ ⋮ Z [ 1 ] ( 1 ) Z [ 1 ] ( 2 ) ⋯ Z [ 1 ] ( m ) ⋮ ⋮ ⋮ ⋮ ] =\begin{bmatrix} \vdots&\vdots&\vdots&\vdots\\ Z^{[1](1)}&Z^{[1](2)}&\cdots&Z^{[1](m)}\\ \vdots&\vdots&\vdots&\vdots \end{bmatrix} =⎣⎢⎢⎡⋮Z[1](1)⋮⋮Z[1](2)⋮⋮⋯⋮⋮Z[1](m)⋮⎦⎥⎥⎤
即 Z [ 1 ] = [ ⋮ ⋮ ⋮ ⋮ Z [ 1 ] ( 1 ) Z [ 1 ] ( 2 ) ⋯ Z [ 1 ] ( m ) ⋮ ⋮ ⋮ ⋮ ] Z^{[1]}=\begin{bmatrix} \vdots&\vdots&\vdots&\vdots\\ Z^{[1](1)}&Z^{[1](2)}&\cdots&Z^{[1](m)}\\ \vdots&\vdots&\vdots&\vdots \end{bmatrix} Z[1]=⎣⎢⎢⎡⋮Z[1](1)⋮⋮Z[1](2)⋮⋮⋯⋮⋮Z[1](m)⋮⎦⎥⎥⎤
5.A[1]矩阵表示样本集中m个样本的第一层的激发向量
A [ 1 ] = σ ( Z [ 1 ] ) A^{[1]}=\sigma(Z^{[1]}) A[1]=σ(Z[1])
A [ 1 ] = [ ⋮ ⋮ ⋮ ⋮ a [ 1 ] ( 1 ) a [ 1 ] ( 2 ) ⋯ a [ 1 ] ( m ) ⋮ ⋮ ⋮ ⋮ ] A^{[1]}=\begin{bmatrix} \vdots&\vdots&\vdots&\vdots\\ a^{[1](1)}&a^{[1](2)}&\cdots&a^{[1](m)}\\ \vdots&\vdots&\vdots&\vdots\\ \end{bmatrix} A[1]=⎣⎢⎢⎡⋮a[1](1)⋮⋮a[1](2)⋮⋮⋯⋮⋮a[1](m)⋮⎦⎥⎥⎤
9.神经网络的梯度下降法
好了,经过上一小结的复习,我们已经清楚了双层神经网络各个符号的意义,下面我们开始研究神经网络的梯度下降法

神经网络的梯度下降过程与logistic回归的梯度下降大致相同,只是多了一些参数
J ( W [ 1 ] , b [ 1 ] , W [ 2 ] , b [ 2 ] ) = 1 m ∑ i = 1 m L ( y ^ , y ) , ( y ^ = a [ 2 ] ) J(W^{[1]},b^{[1]},W^{[2]},b^{[2]})=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y},y),(\hat{y}=a^{[2]}) J(W[1],b[1],W[2],b[2])=m1i=1∑mL(y^,y),(y^=a[2])
然后重复m次梯度下降(这里我没听懂)
计算这些导数的公式如下图

d Z [ 2 ] = A [ 2 ] − Y , Y = [ y ( 1 ) y ( 2 ) ⋯ y ( m ) ] dZ^{[2]}=A^{[2]}-Y,Y=\begin{bmatrix} y^{(1)}&y^{(2)}&\cdots&y^{(m)} \end{bmatrix} dZ[2]=A[2]−Y,Y=[y(1)y(2)⋯y(m)]
d W [ 2 ] = 1 m d Z [ 2 ] A [ 1 ] T dW^{[2]}=\frac{1}{m}dZ^{[2]}A^{[1]T} dW[2]=m1dZ[2]A[1]T
d b [ 2 ] = 1 m n p . s u m ( d Z [ 2 ] , a x i s = 1 , k e e p d i m s = T r u e ) db^{[2]}=\frac{1}{m}np.sum(dZ^{[2]},axis=1,keepdims=True) db[2]=m1np.sum(dZ[2],axis=1,keepdims=True)
d Z [ 1 ] = W [ 2 ] T d Z [ 2 ] ∗ g [ 1 ] ′ ( Z [ 1 ] ) ( 两 矩 阵 之 间 各 元 素 相 乘 ) dZ^{[1]}=W^{[2]T}dZ^{[2]}*g^{[1]'}(Z^{[1]})(两矩阵之间各元素相乘) dZ[1]=W[2]TdZ[2]∗g[1]′(Z[1])(两矩阵之间各元素相乘)
d W [ 1 ] = 1 m d Z 1 X T dW^{[1]}=\frac{1}{m}dZ^{1}X^{T} dW[1]=m1dZ1XT
d b [ 1 ] = 1 m n p . s u m ( d Z [ 1 ] , a x i s = 1 , k e e p d i m s = T r u e ) db^{[1]}=\frac{1}{m}np.sum(dZ^{[1]},axis=1,keepdims=True) db[1]=m1np.sum(dZ[1],axis=1,keepdims=True)
下图为logistic回归的反向传播(对比)

10.直观理解反向传播
这是logistic回归的正向与反向传播的流程图
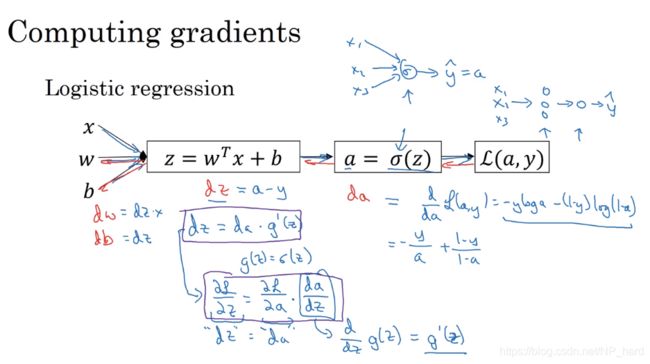
可见da,dz,dw,db都满足一些规律
d z = d a ∗ g ′ ( z ) dz=da*g^{'}(z) dz=da∗g′(z)
d w = d z ∗ x , d b = d z dw=dz*x,db=dz dw=dz∗x,db=dz
下图为神经网络的梯度下降的流程图
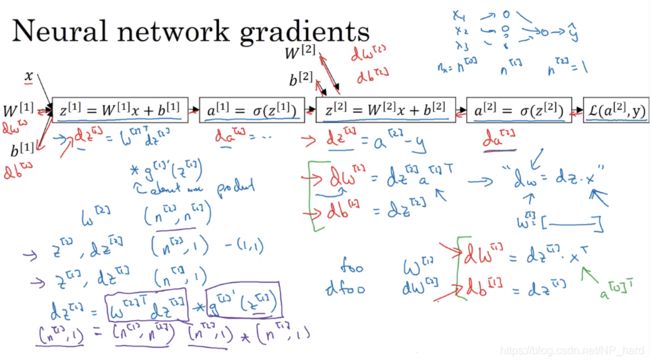
注意,在神经网络中求dW[2]时
d W [ 2 ] = d z [ 2 ] ∗ a [ 1 ] T dW^{[2]}=dz^{[2]}*a^{[1]^{T}} dW[2]=dz[2]∗a[1]T
而在logistic回归中
d w = d z ∗ x dw=dz*x dw=dz∗x
相差了一个转置
矩阵计算时要满足维度相等
这里免去深入理解(太懒了,下次补)
11.随机初始化
如何初始化参数?
在logistic回归中,你当然可以将w和b初始化为0,但是在训练神经网络时,b可以初始化为0,但w不能(w应初始化为随机数)
那么,这是为什么呢?
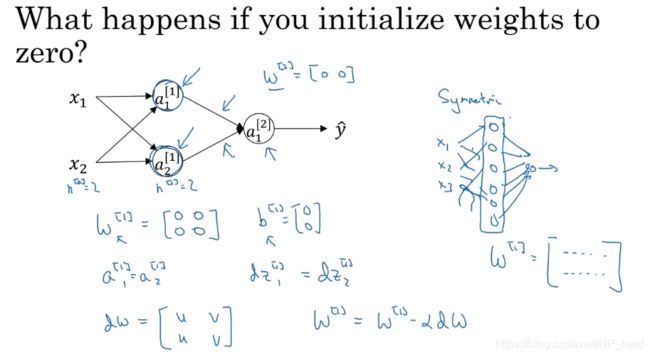
如上图所示,如果你将W[1]初始化为全为0的二阶方阵,那么对于任意两个样本,它们所计算出的a[1]1,a[1]2是完全相同的,因为这两个节点在做相同的运算,可以证明在进行反向传播时,由于对称性,dz[1]1,dz[1]2也是完全相同的,所以设置多个隐藏层毫无意义这里我解释的一般
(第一个隐藏层中的每个神经元将执行相同的计算。因此,即使经过多次梯度下降迭代,层中的每个神经元也会像其他神经元一样计算相同的东西)
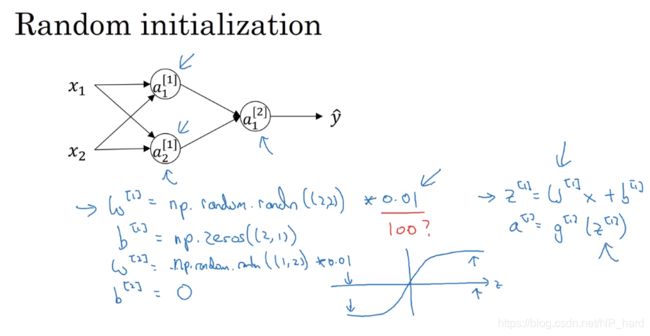
所以我们应该初始化w为2阶方阵,方阵的每个元素都服从高斯分布
那为什么W[1]要乘以0.01呢?
这是因为如果你的激活函数为tanh或者sigmoid函数,当z很大时,梯度下降的速度会变慢,所以人们希望W[1]初始化为较小的数
3.深度神经网络
本章的大部分概念与单隐藏层神经网络十分相似,故不作深入讲解
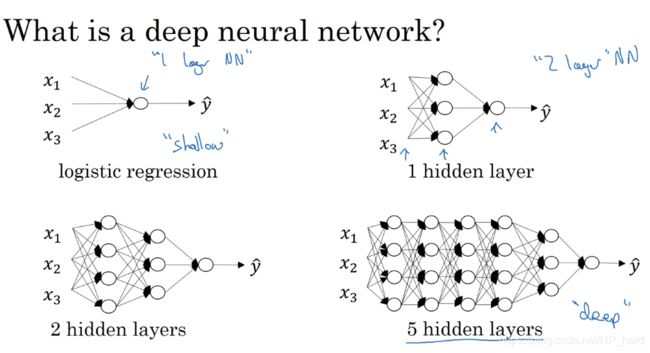
1.深层神经网络
2.深层网络中的正向传播
和单隐藏层神经网络的正向传播十分相似,只不过需要循环L次,即循环隐藏层的层数次
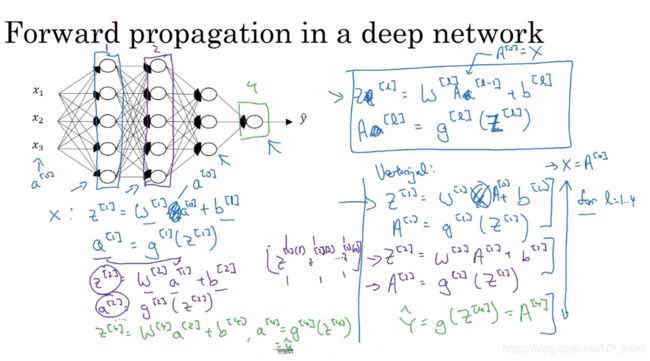
3.核对矩阵的维数
这一小节主要讲一讲一些参数的固定维数
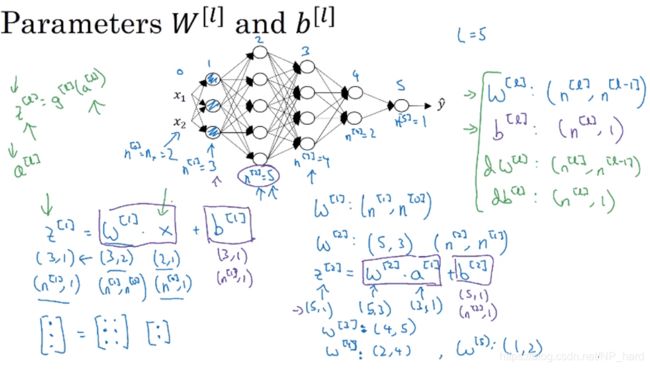
W [ l ] : ( n [ l ] , n [ l − 1 ] ) , b [ l ] : ( n [ l ] , 1 ) W^{[l]}:(n^{[l]},n^{[l-1]}),b^{[l]}:(n^{[l]},1) W[l]:(n[l],n[l−1]),b[l]:(n[l],1)
d W [ l ] : ( n [ l ] , n [ l − 1 ] ) , d b [ l ] : ( n [ l ] , 1 ) dW^{[l]}:(n^{[l]},n^{[l-1]}),db^{[l]}:(n^{[l]},1) dW[l]:(n[l],n[l−1]),db[l]:(n[l],1)
发现了没有,W和b这两个参矩阵的维数是不随样本数m的改变而改变的!
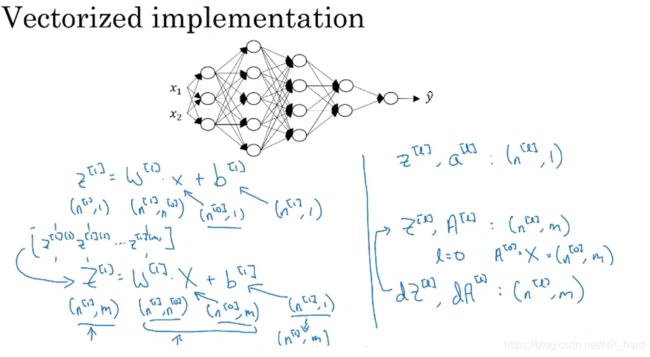
z [ l ] , a [ l ] : ( n [ l ] , 1 ) z^{[l]},a^{[l]}:(n^{[l]},1) z[l],a[l]:(n[l],1)
{ Z [ l ] , A [ l ] : ( n l , m ) d Z [ l ] , d A [ l ] : ( n l , m ) \begin{cases}Z^{[l]},A^{[l]}:(n^{l},m) \\ \\ dZ^{[l]},dA^{[l]}:(n^{l},m) \end{cases} ⎩⎪⎨⎪⎧Z[l],A[l]:(nl,m)dZ[l],dA[l]:(nl,m)
而Z和A这两个参数矩阵是随样本数的改变而改变的
4.为什么使用深层表示
首先举个例子,神经网络如何进行人脸识别?
神经网络是先寻找一些像素点,这些点亮(激发)的像素点会在下一层中点亮一小块皮肤或者眼睛,嘴巴,然后这些小特征在下一层中会点亮眼睛,鼻子,耳朵…最后点亮一张人脸,这大概就是为什么我们需要多隐藏层的神经网络了
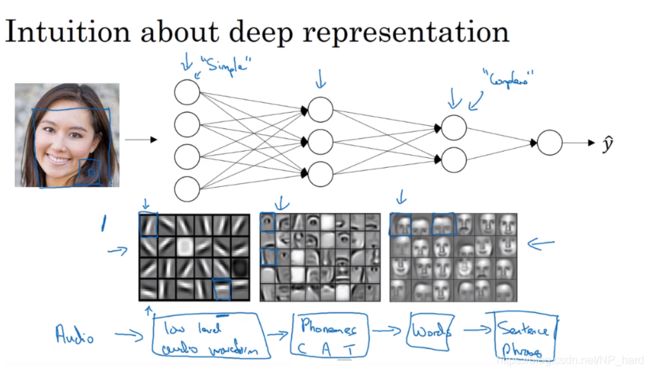
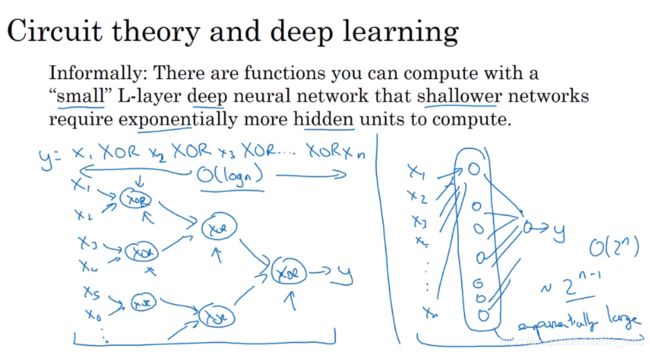
另外,在一些电路理论中,如果你想要减少神经网络的层数,那么单个隐藏层的单元个数可能指数增长
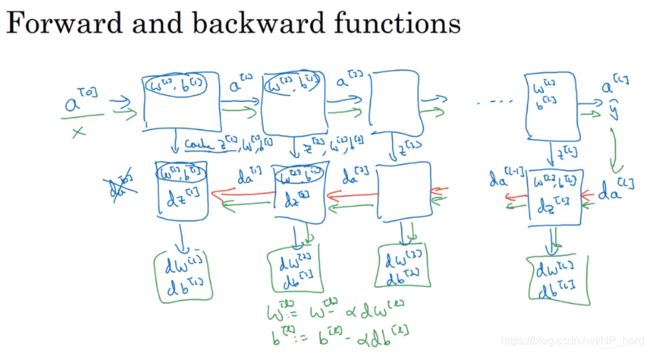
5.搭建深层网络块
那么我们如何搭建深层网络块呢?
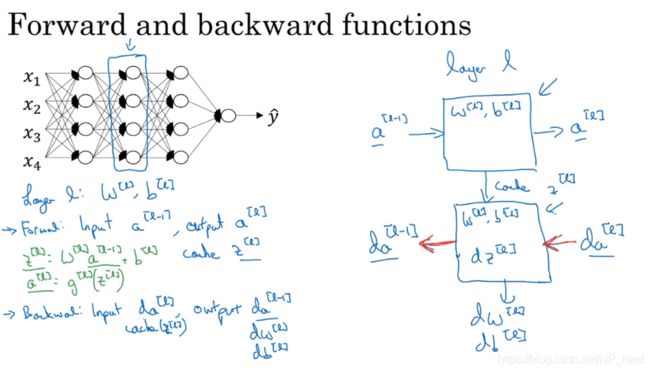
对于神经网络第l层来说,正向传播和反向传播可以简单抽象为如下图所示的两个模块,正向传播时,输入a[i-1],输出a[i],需要使用参数w[i],b[i],cache z[i]
def forward_propagation(A_i_1, parameters):
Wi = parameters['Wi']
bi = parameters['bi']
Zi = np.dot(Wi, A_i_1) + bi
Ai = np.tanh(Zi)
cache = {
"Zi": Zi,
"Ai": Ai,}
return Ai, cache
而在反向传播时,输入da[i],输出da[i-1],dw[i],db[i]
这里的代码未更正
def backward_propagation(parameters, cache, X, Y):
m = X.shape[1]
W1 = parameters['W1']
W2 = parameters['W2']
A1 = cache['A1']
A2 = cache['A2']
dZ2 = A2 - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
grads = {
"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
6.前向和反向传播
#计算第i层的线性值,返回第i层的参数和A_prev
def linear_forward(A, W, b):
Z = np.dot(W, A) + b
assert (Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
#计算第i层的激活值
def linear_activation_forward(A_prev, W, b, activation):
if activation == "sigmoid":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
#计算每一层的激发值,返回预测值和包含每一层参数的cashes
def L_model_forward(X, parameters):
caches = []
A = X
L = len(parameters) // 2
for l in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], 'relu')
caches.append(cache)
AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], 'sigmoid')
caches.append(cache)
assert (AL.shape == (1, X.shape[1]))
return AL, caches
#计算第i层的dW,db,dA_prev
def linear_backward(dZ, cache):
A_prev, W, b = cache
m = A_prev.shape[1]
dW = (1 / m) * np.dot(dZ, A_prev.T)
db = (1 / m) * np.sum(dZ, axis=1, keepdims=True)
dA_prev = np.dot(W.T, dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
#通用性更强的linear_backward,返回第i层的dW,db,dA_prev
def linear_activation_backward(dA, cache, activation):
linear_cache, activation_cache = cache
#根据不同的激发函数计算dZ
if activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
#整个神经网络进行反向传播,返回装有所有微分的grads
def L_model_backward(AL, Y, caches):
grads = {
}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
#先计算最后一层的dAL
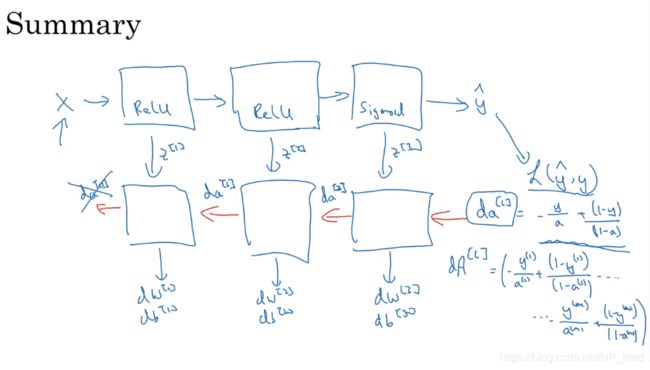
dAL = -(np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
current_cache = caches[L - 1]#最后一层的参数
#计算最后一层的梯度
grads["dA" + str(L - 1)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL,current_cache,"sigmoid")
for l in reversed(range(L - 1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 1)], current_cache, "relu")
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
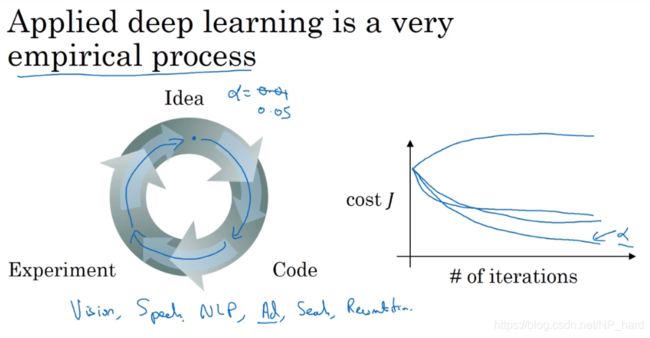
7.参数与超参数
这一小节主要解释了什么是参数,什么是超参数,深入的讲解会在进阶的视频

8.这和大脑有什么关系?
9.搭建一个多隐藏层的神经网络代码实现
import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCase import *
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
np.random.seed(1)
#给神经网络的每个隐藏层初始化参数w和b
def initialize_parameters_deep(layer_dims):
np.random.seed(3)
parameters = {
}
L = len(layer_dims)
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l - 1]) * 0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
assert (parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
assert (parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parameters
#计算第i层的线性值,返回第i层的参数和A_prev
def linear_forward(A, W, b):
Z = np.dot(W, A) + b
assert (Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
#计算第i层的激活值
def linear_activation_forward(A_prev, W, b, activation):
if activation == "sigmoid":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
#计算每一层的激发值,返回预测值和包含每一层参数的cashes
def L_model_forward(X, parameters):
caches = []
A = X
L = len(parameters) // 2
for l in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], 'relu')
caches.append(cache)
AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], 'sigmoid')
caches.append(cache)
assert (AL.shape == (1, X.shape[1]))
return AL, caches
#计算损失值
def compute_cost(AL, Y):
m = Y.shape[1]
logprobs = np.multiply(Y, np.log(AL)) + np.multiply(1 - Y, np.log(1 - AL))
cost = (-1 / m) * np.sum(logprobs)
cost = np.squeeze(cost)
assert (cost.shape == ())
return cost
#计算第i层的dW,db,dA_prev
def linear_backward(dZ, cache):
A_prev, W, b = cache
m = A_prev.shape[1]
dW = (1 / m) * np.dot(dZ, A_prev.T)
db = (1 / m) * np.sum(dZ, axis=1, keepdims=True)
dA_prev = np.dot(W.T, dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
#通用性更强的linear_backward,返回第i层的dW,db,dA_prev
def linear_activation_backward(dA, cache, activation):
linear_cache, activation_cache = cache
#根据不同的激发函数计算dZ
if activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
#整个神经网络进行反向传播,返回装有所有微分的grads
def L_model_backward(AL, Y, caches):
grads = {
}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
#先计算最后一层的dAL
dAL = -(np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
current_cache = caches[L - 1]#最后一层的参数
#计算最后一层的梯度
grads["dA" + str(L - 1)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL,current_cache,"sigmoid")
for l in reversed(range(L - 1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 1)], current_cache, "relu")
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
#更新参数
def update_parameters(parameters, grads, learning_rate):
L = len(parameters) // 2
for l in range(L):
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads['dW' + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters
完结撒花!