线性表链式存储结构
前言
前面复习完了线性表。这里略微进行优缺点的分析。优点很明显,其是一个数组,数组操作简便,分析较为容易。那缺点呢?实则也很明显,事先不知道数据大小的时候只能往大的空间开,插入删除操作伴随着大量数据的移动。
(当然了自己测试的都是些小数据)
针对以上的缺点,一种名为“链表”的神奇物种就诞生了!
怎么解决的这么多弱点呢,请听下面分解。
啊对了,这之后需要稍微停更一会,要先把实习DEHAZE的算法流程图做完还要讨论可实施性。
一、学习目标:
了解链表的定义,掌握链表的基本操作,基本的时间复杂度。
学习内容:
1、 链表的定义 2、 链表的基本操作 3、 时间复杂度分析 4、 LeetCode真题实战链表定义
什么叫做“链”?反正我第一个想到的是拴狗链,你拿条绳子系在狗脖子上那就是链。紧接着我想到水浒里的呼延灼把马链在一起,还有赤壁之战曹操的战船也用铁索相连。扯远了。。。
但有一个共通性就是说链式结构数据之间有紧密的联系,一个数据会锁住(指向)另一个数据。
相信话至此大佬们都能明白这其中蕴含了“指针”的思想吧!
那官方定义是长啥样的?

链表的基本操作
数据结构通篇都包含的一个操作就是建立操作。
我们要建链表,然后同样地往其中进行增删查。(数据库拿了A+,我很高兴,Edinburgh的老师就是不一样一点哈哈)
由于链表至少会存储两个域的信息(如上定义所示),因此需要事先声明一个结构体,然后同样以类的形式来进行封装(以后就不赘述啦,原谅我最后一次多嘴)。
struct LNode{
int data;
int index; // 为了多项式相加设计的 指数保存域
LNode *next;
LNode *prior; // 为了双向链表设计的前向指针
};
class LinkList{
// 设为保护属性是为了继承时操作更加方便能直接访问
protected:
// 头结点的含义下面有讲解
LNode *head;
int length;
public:
LinkList();
LNode *GetList() {
return head; }
int GetLen() {
return length; }
/*
设计成虚函数的目的是重载。循环链表,双向链表,
多项式等都需要进行小修小改
*/
virtual void CreateList(int* a, int l);
virtual void Insert(int pos, int val);
virtual void Delete(int pos);
void Find(int n);
bool Exist(int num);
LinkList MergeList(LinkList t);
void ShowList();
~LinkList() {
delete[] head; }
};
那么如何进行建表操作呢?
这里有两种实施方案:一是设计一个空头结点,此结点会指向实际包含了数据的第一个结点;二则是舍弃这个头结点,保存的第一个结点就是有实际数据的。
这里我们采用的是第一种方案。没有孰好孰坏,只是熟悉与否。因为我们上课时老师基本采用的第一种哈。
哦对了,在这之前要先进行初始化操作。由于我们采用第一种,那么初始化操作长下面的样子:(无非就是为头结点开辟空间,为其赋上一个随机值,同时指向空)
LinkList::LinkList(){
head = new LNode;
head->data = mmax;
head->next = NULL;
}
建表方式很多,可以输入一个值插入一个对应结点,我这儿用到的是一个数组进行初始化。
void LinkList::CreateList(int *a, int l){
length = l;
int cur = 0;
LNode *p = head;
while(cur < l){
LNode *node = new LNode;
node->data = a[cur++];
node->next = NULL;
p->next = node;
p = p->next;
}
ShowList();
}
建表时很重要的一个点在于要先用一个p指向与head相同的地址。为啥要这样做?为啥不直接移动head?
你想,如果直接移动head,那么插入结束后head就在链表末端,那么进行链表展示时,从head开始输出是不是就有问题了! 于是乎,需要用到另一个指针进行操作。这样一来相当于这么一个流程,如图所示:
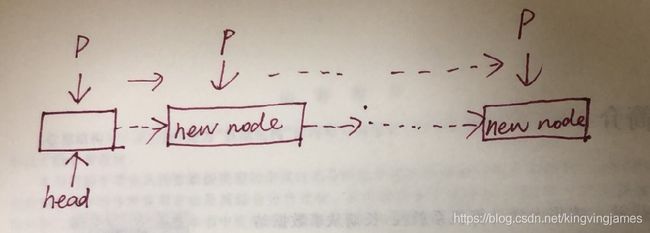
根据这个流程图来反观代码实际上就是:
每次p都在待插入结点之前的位置。当我们生成一个新节点时,为其附上合适的属性。然后把此节点链在p之后。最后再把p移动到此位置上。
(属性:值就是对应到传入数组的值;next总是先设为NULL,因为后续有无结点并不清楚[当然了,自己想判断也行,但默认这么做较为方便,因为后续假如有结点那么此NULL值会被后续的那一个结点替代。] p移动:如果p不移动的话,p->next始终指向同一地址,那么元素就是不断地覆盖同一地址最后就会出错。)
接下来就是插入Insert的实现了,这里实际上和建表的流程大同小异:
void LinkList::Insert(int pos, int val){
if(pos > length || pos < 0){
cout << "插入位置不正确,无法插入" << endl;
}
LNode *p = head;
int cur = 0;
while(cur < pos){
p = p->next;
cur++;
}
LNode* node = new LNode;
node->data = val;
node->next = p->next;
p->next = node;
length++;
ShowList();
}
记住,我们插入时要找到的是待插入位置的前一个结点!!
为啥不找刚好那个位置的节点呢?
先思考插入需要的步骤!插入位置之前的那个结点要链接到此新结点,此新结点链接原来在此处的结点,结合图示:
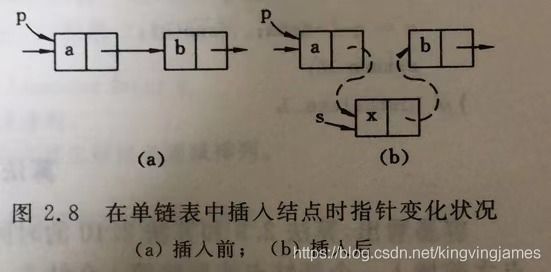
这里存在和上一章线性表同样的问题,就是位置信息的问题。我的位置pos用的直接是索引下标,即引入0这个位置。但上次也提到过,一些OJ是从1开始的,自己注意即可。
删除操作可想象成从上图的 b -> a。那么经历了什么操作?
仍旧是找到待删除的前一个结点,即找到a,直接把a的next链到b即可:即跳过x就行,其余都不用修改。当然了最好的话是先拿一个指针指向x地址,再进行修改,最后对x进行释放内存。(不能先释放内存,否则a->next直接为空,将永远找不到b。)
void LinkList::Delete(int pos){
if(pos < 0 || pos > length){
cout << "删除的位置有误,无法删除";
}
length--;
LNode *p = head;
int cur = 0;
while(cur < pos){
p = p->next;
cur++;
}
LNode *node = p->next;
p->next = p->next->next;
delete[] node;
ShowList();
}
查操作实际上和Show函数没区别。实际上都是学会对链表的遍历!
对链表遍历很容易啦,从头结点开始不断next下去,直到空就停止啦,当然也可以利用保存着的长度length进行遍历,都行!(第一种稍微主流一点好像 )
bool LinkList::Exist(int num){
LNode *p = head->next;
while(p){
if(p ->data == num){
return true;
}
p = p->next;
}
return false;
}
void LinkList::ShowList(){
LNode *p = head->next;
while(p){
cout << p->data << " ";
p = p->next;
}
cout << endl;
}
紧接着就是链表的合并了,思想和线性表那个合并一模一样(线性表保持顺序合并),直接看代码也不难:
(保持的是递减顺序不变!!)
LinkList LinkList::MergeList(LinkList t){
LNode *p = t.GetList();
LNode *q = head;
cout << "以下是合并过程: \n";
LinkList merge;
int k = 0; // 代表插入位置, 每次执行Insert函数后插入位置往后挪1
while(p->next && q->next){
if(p->next->data > q->next->data){
merge.Insert(k++, p->next->data);
p = p->next;
}
else{
merge.Insert(k++, q->next->data);
q = q->next;
}
}
while(p->next){
merge.Insert(k++, p->next->data);
p = p->next;
}
while(q->next){
merge.Insert(k++, q->next->data);
q = q->next;
}
merge.ShowList();
return merge;
}
按照书上的进度的话接下来会用线性表的形式来完成链式结构,但由于我们课上完全没提我也不提了。(貌似)
好der,那么接下来就是另两种形式的链表即循环链表和双向链表。
前者很简单,实际上就是把尾结点链接到自己的头就好了。(不知道为啥莫名想到了贪吃蛇) 其余操作都不用改动,可以自行修改一下Show函数。这里就可以体现利用长度输出的好处了,不断判断next的方法话由于收尾相连会陷入死循环即无限输出!反观设置了长度值就可以输出固定的数量就好了。
这里用到了继承的思想,忘了的朋友可以自己略加复习哈(虽然我也就记得那么点):
class Circular_Linked_List:public LinkList{
// 主要的特别之处在于链表尾结点会链接到头结点
public:
void CreateList(int *a, int l);
// 因此展示链表元素时会无限输出
// 如果不想要此效果的话也把 show函数改为虚函数,然后进行重载
/*
插入 删除等基础操作都不受影响
*/
};
void Circular_Linked_List::CreateList(int* a, int l){
length = l;
int cur = 0;
LNode *p = head;
while(cur < l){
LNode *node = new LNode;
node->data = a[cur++];
node->next = NULL;
p->next = node;
p = p->next;
}
p->next = head->next;
//ShowList();
}
双向链表细心的小伙伴肯定在文章一开始就注意到啦!就是那个prior前向指针!
那实际上就是说一个结点如果有前继结点prior指针应该指向这个前继。整体修改如下:
class Double_Linked_List:public LinkList{
public:
Double_Linked_List();
void CreateList(int *a, int l);
void Insert(int pos, int val);
void Delete(int pos);
/*
这里的插入与删除操作与书本略有些不同
书本是找到刚好要插入或删除的那个结点然后进行操作的
但本人由于懒,直接拿基类的操作来套:
于是找到的仍是待插入或删除的前一个结点,从那个结点出发进行操作
*/
};
Double_Linked_List::Double_Linked_List(){
head = new LNode;
head->data = mmax;
head->next = NULL;
head->prior = NULL;
}
void Double_Linked_List::CreateList(int* a, int l){
length = l;
int cur = 0;
LNode *p = head;
while(cur < l){
LNode *node = new LNode;
node->data = a[cur++];
node->next = NULL;
node->prior = p;
p->next = node;
p = p->next;
}
ShowList();
}
void Double_Linked_List::Insert(int pos, int val){
if(pos > length || pos < 0){
cout << "插入位置不正确,无法插入" << endl;
}
LNode *p = head;
int cur = 0;
while(cur < pos){
p = p->next;
cur++;
}
LNode* node = new LNode;
// 对于这个新节点有如下情况需要进行添加
// 原本位于这个位置的结点现在被强制移到其之后,那么其prior需要被修改
// 这个位置的结点前面那个点的next会被修改
// 一定要注意顺序,因为指针被修改后会有较大影响
node->data = val;
p->next->prior = node;
node->next = p->next;
node->prior = p;
p->next = node;
length++;
ShowList();
}
void Double_Linked_List::Delete(int pos){
if(pos < 0 || pos > length){
cout << "删除的位置有误,无法删除";
}
length--;
LNode *p = head;
int cur = 0;
while(cur < pos){
p = p->next;
cur++;
}
LNode *node = p->next;
// p->next->next->prior = p;
if(p->next->next!=NULL){
p->next->next->prior = p;
}
p->next = p->next->next;
delete[] node;
ShowList();
}
建表时,在p移动到当前结点之前需要让当前结点前继设为p(注意顺序,如果先移动了p那么前继就指向了自己就没有意义了!)。
插入一个结点时要修改的地方就较多。还是以插入图示为例,在上方。
插入的x的前继要设为a,x的后继要设为b,a的后继要更新为x,b的前继要更新为x。当前我们的指针停在a的位置,且a的后继还是b。
此时执行步骤是这样的:
p->next->prior = node;
node->next = p->next;
node->prior = p;
p->next = node;
一定要按顺序!!!指针不能乱移动,否则链接的关系会紊乱!!
删除就大噶自己想一想吧,结合代码想也阔以的。
这里值得注意的一点是双向链表的增删操作,书上算法实现是直接遍历到需要进行操作的那个位置的,但我仍然是遍历到需要操作的之前那个位置,本质都一样哈!
最后,教材上的内容就是利用链式存储结构来完成多项式的相加。
针对多项式我们不能简单的用int型数组进行操作,需要一个包含系数与指数的结构体来实现:
struct Poly{
int index;
int coefficient;
};
实际上整个多项式的相加和MergeList合并函数的思想仍旧是差不多的:
// 利用线性链表结构来实现多项式相加
class Polynomial:public LinkList{
public:
void CreateList(Poly* a, int l);
void PolyAdd(Polynomial s);
void Append(int pos, int index, int coeff);
void ShowList();
};
void Polynomial::ShowList(){
LNode *p = head->next;
int cnt = 0;
while(p){
if(p->data != 0){
if(p->data > 0 && cnt != 0){
cout << '+';
}
if(p -> index == 0){
cout << p->data;
}
else if(p -> index == 1){
cout << p->data << 'x';
}
else{
cout << p->data << "x^" << p->index;
}
cnt++;
}
p = p->next;
}
cout << endl;
}
void Polynomial::Append(int pos, int index, int coeff){
if(pos > length || pos < 0){
cout << "插入位置不正确,无法插入" << endl;
}
LNode *p = head;
int cur = 0;
while(cur < pos){
p = p->next;
cur++;
}
LNode *q = new LNode;
q->index = index;
q->data = coeff;
q->next = p->next;
p->next = q;
length++;
}
void Polynomial::CreateList(Poly* a, int l){
length = l;
int cur = 0;
LNode *p = head;
while(cur < l){
LNode *node = new LNode;
node->data = a[cur].coefficient;
node->index = a[cur++].index;
node->next = NULL;
p->next = node;
p = p->next;
}
ShowList();
}
void Polynomial::PolyAdd(Polynomial s){
LNode *p = s.GetList();
LNode *q = head;
Polynomial result;
int k = 0;
while(p->next && q->next){
if(p->next->index < q->next->index){
result.Append(k++, p->next->index, p->next->data);
p = p->next;
}
else if(p->next->index > q->next->index){
result.Append(k++, q->next->index, q->next->data);
q = q->next;
}
else{
result.Append(k++, q->next->index, q->next->data + p->next->data);
p = p->next;
q = q->next;
}
}
while(p->next){
result.Append(k++, p->next->index, p->next->data);
p = p->next;
}
while(q->next){
result.Append(k++, q->next->index, q->next->data);
q = q->next;
}
result.ShowList();
}
稍微解释一下:
重载建表函数是因为我们用的是Poly数组进行创建的,实际操作和单链表完全一致。而Append函数无法进行重载是因为函数的参数个数不再相同因此不能直接进行Insert重载(我记得是这样的因此才建了一个新函数)。展示的Show函数也进行修改是为了让其更加符合一个多项式的输出方式。
最后就是PolyAdd,是主要进行相加步骤的函数。思路如下:
首先我们默认是规则的多项式,即指数是递增的。
两个多项式中指数小的结点会被直提取其数据直接Append入结果中。然后指针往后移。如若指数相同则系数需要进行加操作,然后同样把结果Append入结果中。
最后仍旧需要考虑某一链表遍历完毕但另一方还没完成的情况,于是两个while消除此影响。
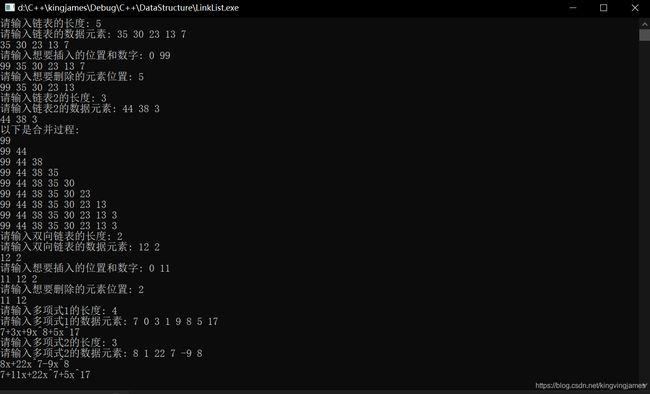
好了最后附上运行的测试图:
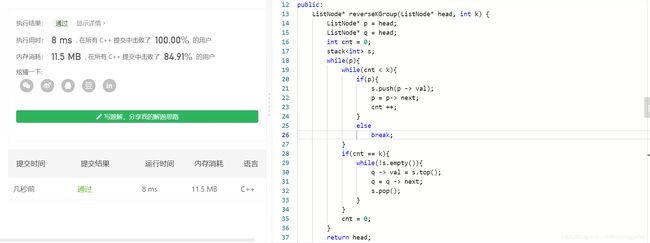
绿题来啦!
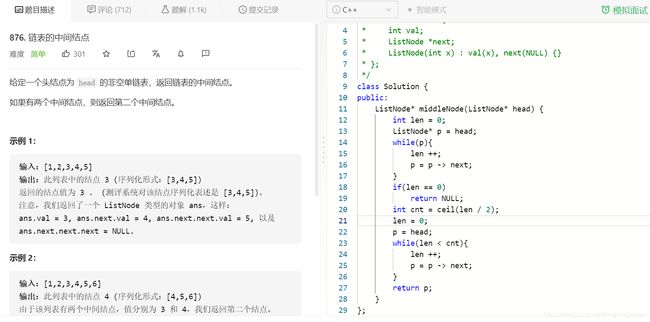
这一题用到的知识就是链表的遍历啦,由于其代码并未包含length于是我们需要自己先求解长度。然后取中遍历到相应结点即可完成。
变黄

因为这一题需要逆序处理,所以很容易想到栈处理。因为加法都是从个位先的嘛!
但由于还没复习到栈这一数据结构我一开始是 利用循环把链表的数保存下来,比如例题中就是记录为 7243 + 564,再用while循环把每次进行模10和除10取整运算,把每个数算出来后作为一个结点进行操作即可。
但WA了,因为存在了一个超长的链表使得我用 long long都不足以存储,因此最后还是只能用到栈。特意写成Merge函数的形式为了便于理解,代码如下:
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* p = l1;
ListNode* q = l2;
stack<int> s1;
stack<int> s2;
stack<int> result;
while(p){
s1.push(p -> val);
p = p -> next;
}
while(q){
s2.push(q -> val);
q = q -> next;
}
bool flag = false;
int temp;
while(!s1.empty() && !s2.empty()){
temp = s1.top() + s2.top() + (flag == false ? 0 : 1);
if(temp >= 10){
flag = true;
result.push(temp - 10);
}
else{
flag = false;
result.push(temp);
}
s1.pop(), s2.pop();
}
while(!s1.empty()){
temp = s1.top() + (flag == false ? 0 : 1);
if(temp >= 10){
flag = true;
result.push(temp - 10);
}
else{
flag = false;
result.push(temp);
}
s1.pop();
}
while(!s2.empty()){
temp = s2.top() + (flag == false ? 0 : 1);
if(temp >= 10){
flag = true;
result.push(temp - 10);
}
else{
flag = false;
result.push(temp);
}
s2.pop();
}
if(flag)
result.push(1);
ListNode* head = new ListNode;
p = head;
while(!result.empty()){
p -> val = result.top();
result.pop();
if(!result.empty()){
p -> next = new ListNode;
p = p -> next;
}
}
return head;
}
};
这儿就先也不细讲了,因为涉及到了栈,但栈下一次就会复习到啦!!
这一题由于题目限制是单链表会限制发挥空间,实际上用双向链表包含了prior指针的话不就可以先遍历到底部然后直接逆着操作了么?不就十分简单了吗,可以自己试一试哈,很简单的!!