数据结构:链式二叉树及其相关算法
在上一篇树和堆的博客中,有关树的定义已经详细地介绍过了。今天我们要详细介绍的是链式二叉树。链式二叉树,就是它不再是满二叉树或者是完全二叉树,因此不再适合使用数组存储,因此它以链表为基础结构,一个节点中保存着两个地址,指向它的左右孩子。
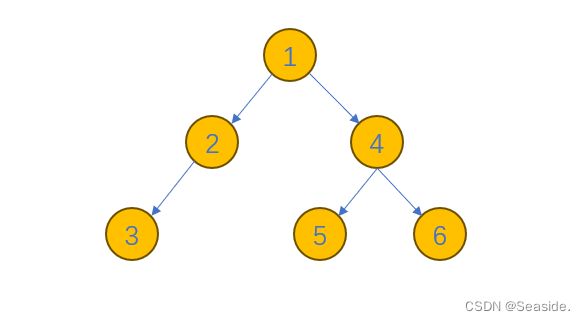
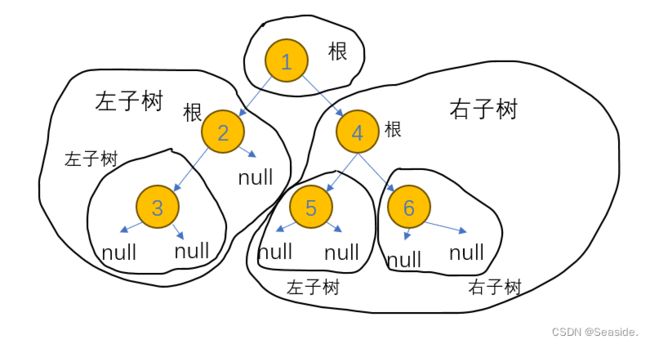
我们要这样看二叉树:总是将它分成左子树和右子树。如上图这个二叉树可以分为以2为根的左子树、以3为根的右子树。而每个子树又可以分为小子树,小子树又可以分为小小子树。直到它们不可再分为止。例如4的左子树为空,右子树也为空。直到这个节点没有孩子为止。这时遍历二叉树的基本思想。
一、二叉树的遍历
二叉树有四种遍历方法:前序遍历、中序遍历、后序遍历、层序遍历。
1.前序遍历
它的遍历方法为先访问根,再访问左子树的根,最后访问右子树的根。以上图的这个二叉树为例,前序遍历先访问根,也就是1,再访问左子树的根,也就是2,接着再访问左子树的根,也就是3,然后再访问左子树的根,是NULL(下文简称为N),当遇到N时3的左子树就算访问完毕了。接着访问3的右子树,也是N,这时2的左子树就访问完毕了。然后访问2的右子树。2的右子树根为N,之后2的右子树访问完毕,此时1的左子树也访问完毕了。开始访问1的右子树的根4。1的右子树也含有有小左子树5,那就访问小左子树5,访问完5后访问5的左子树根,是N,之后访问5的右子树,也是N,此时4的左子树就访问完毕了。之后访问4的右子树,根为6,再访问6的左子树,为N,再访问6的右子树,也为N,此时6的右子树访问完毕,也代表4的左子树也访问完毕了,也代表1的右子树也访问完毕了。此时这棵树的所有节点全部访问完毕了。访问的顺序为1,2,3,N,N,N,4,5,N,N,6,N,N。观察这棵树,你会发现,1为这棵树的根,2,3,N,N,N为这棵树的左边的全部节点,4,5,N,N,6,N,N为这棵树的右节点,因此前序遍历的记忆口诀为根,左子树,右子树。
通过对前序遍历的特性进行分析,可以发现,要想实现前序遍历,就访问它的左右子树,然后再访问子树的子树,就好像递归一样,把一个大问题拆分为若干个小问题。
算法实现:
// 二叉树前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
else
{
printf("%d ", root->_data);
PreOrder(root->_left);
PreOrder(root->_right);
}
}也可以自己画一下递归展开图,加深一下代码的理解。
2.二叉树前序遍历并返回遍历数组
void PreOrder(struct TreeNode* root, int* a, int* pi)
{
if(root == NULL)
{
return;
}
else
{
a[(*pi)++] = root->val;
PreOrder(root->left, a, pi);
PreOrder(root->right, a, pi);
}
}
int BinaryTreeSize03(struct TreeNode* root)
{
return root == NULL ? 0 : BinaryTreeSize03(root->left) + BinaryTreeSize03(root->right) + 1;
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
int i = 0;
*returnSize = BinaryTreeSize03(root);
int* a = malloc(sizeof(int) * (*returnSize));
PreOrder(root, a, &i);
return a;
}3.中序遍历和后序遍历
中序遍历的方法是先访问左子树,再访问根,最后访问右子树。分析过程和前序遍历一样,它先访问左子树,一直访问左子树,直到遇到空为止。以上图的二叉树为例,它先访问的是3的左子树,是N,再访问根,是3,再访问右子树,是N,此时2的左子树访问完毕,访问这个子树的根,是2,再访问这个子树的右子树,为N,此时1的左子树访问完毕,访问根,是1,左子树和根访问完毕,访问右子树,再访问右子树的左子树,一直到空为止,因此下一个要访问的节点为N,它是5的左子树,再访问根,是5,再访问5的右子树,也为N,然后此时4的左子树访问完毕,访问4的根,是4,再访问4的右子树,根为6,要先访问6的左子树,是N,再访问根,为6,再访问右子树,是N。此时这个树就遍历完毕了。
算法实现:
// 二叉树中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
else
{
InOrder(root->_left);
printf("%d ", root->_data);
InOrder(root->_right);
}
}至于后序遍历,它的遍历顺序为左子树,右子树,根。它的遍历顺序为N N 3 N 2 N N 7 N 5 N N 6 4 1,读者可以尝试自己推一下。
代码实现:
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
else
{
PostOrder(root->_left);
PostOrder(root->_right);
printf("%d ", root->_data);
}
}二、求二叉树节点个数
在前文我们讲了二叉树遍历的三种顺序,那么要想求二叉树节点的个数,只需在遍历中加入一个计数器即可。
代码实现:
int BinaryTreeSize02(BTNode* root,int* size)
{
if (root == NULL)
{
return 0;
}
else
{
(*size)++;
BinaryTreeSize02(root->_left,size);
BinaryTreeSize02(root->_right,size);
return (*size);
}
return 0;
}它还有一个更简单的版本:
int BinaryTreeSize03(BTNode* root)
{
return root == NULL ? 0 : BinaryTreeSize03(root->_left)
+ BinaryTreeSize03(root->_right) + 1;
}三、二叉树叶子结点的个数
代码实现:
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root, int* count)
{
if (root == NULL)
{
return 0;
}
else if (root->_left == NULL && root->_right == NULL)
{
return (*count)++;
}
else
{
BinaryTreeLeafSize(root->_left, count);
BinaryTreeLeafSize(root->_right, count);
}
return *count;
}在写递归的时候,想要写好递归,我们首先要确定两个要素:最小子问题和返回条件。当我们想要求叶子结点的个数时,它的最小子问题是求一个最简单的二叉树,而这个最简单的二叉树是只有一个根节点,没有左右孩子的二叉树。返回条件是判断它的左右孩子是否都为空,如果符合该条件就代表这个节点是叶子结点。当我们要求上图所示的二叉树的叶子结点时,我们先分别求左树和右树的叶子结点,那就先判断1,1不是,就判断2,2也不是,就判断3,发现3是个叶子结点,就让count+1,再返回的图中,返回到2节点时,程序会访问右树,而右树是个空节点,那么我们就判断如果这个节点是空节点,那就不让count+1。最后返回到1节点,开始调用右子树,求叶子节点也是使用相同的分析方法。
四、二叉树第k层叶子结点个数
代码实现:
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k, int *count)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return (*count)++;
}
else
{
BinaryTreeLevelKSize(root->_left, k-1, count);
BinaryTreeLevelKSize(root->_right, k-1, count);
}
return (*count);
}上文提到,要想写好递归,就要确定它的最小子问题和返回条件。而求二叉树第k层的叶子结点个数,它的最小子问题是一个只含有根,没有孩子的节点,我们把层数设为k,求第一层的节点,k就等于1,此时直接返回count+1即可。假如说我们有一个二叉树,这个树含有一个根,两个节点,那么我们要想求第二层的节点个数,k就等于2,就像求第一层的节点数一样,k等于1,那么求第二层时,我们给函数传一个k-1,那么在这个函数里面,k等于2,然后进入左子树,k就等于1,并没有改变k的值。传过去之后,k等于1,然后若有节点,就返回count+1,没有则不让count+1。对右子树也是如此。假如说我们想要求上图中二叉树第三层的节点个数,那就设k = 3,接着判断,k等于1就让count+1。之后程序进入左子树,k等于2,在进入左子树,k等于1。此时让count+1。接着返回至2节点处,开始调用右树。但右树为空树,就直接返回。
五、二叉树查找值为x的节点地址
代码实现:
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->_data == x)
{
return root;
}
else
{
BTNode* ret1 = BinaryTreeFind(root->_left, x);
BTNode* ret2 = BinaryTreeFind(root->_right, x);
if (ret1 == NULL && ret2 == NULL)
{
return NULL;
}
else if (ret1 == NULL)
{
return ret2;
}
else
{
return ret1;
}
}
}要查找二叉树值为x节点的地址,首先要确定它的最小子问题和返回条件。最小子问题是求一个含有一个根和两个孩子的二叉树,先在查找左孩子,如果左孩子值不为x,就查找右孩子。返回条件是,当左孩子查找到该值时,就使用ret1接受这个返回值;若右孩子查找到该值时,就使用ret2接受这个返回值。若左孩子找到了而右孩子没有找到,那么ret2是NULL,反之,ret1为NULL。只有左右孩子都没有查找到时,就代表此树中没有该值,就返回空。如果ret1存着该值的地址,就返回ret1,反之则返回ret2。
六、判断两个二叉树是否相同
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p == NULL && q == NULL)
{
return true;
}
else if(p!=NULL && q != NULL)
{
if(p->val != q->val)
{
return false;
}
else
{
int ret1 = isSameTree(p->left,q->left);
int ret2 = isSameTree(p->right,q->right);
if(ret1&&ret2)
{
return true;
}
else
{
return false;
}
}
}
else
{
return false;
}
return true;
}判断二叉树是否相同的条件是两个树的结构、值必须相同。先来判断他们的结构是否相同。如果都等于空,就返回true,如果两个不同时为空或不同时不为空,就返回false。要先判断它们的结构存在,才能判断值是否相同。接下来就判断它们的值。如果值不相同,就返回false;之后这个节点就判断完毕,就要调用递归函数判断它们的子树。需要创建两个变量来接收它们的返回值,只要返回值中有false,就证明这连个树不相同。
七、判断二叉树是否为对称二叉树
bool _isSymmetric(struct TreeNode* root1, struct TreeNode* root2)
{
if(root1 == NULL && root2 == NULL)
{
return true;
}
else if(root1 == NULL || root2 == NULL)
{
return false;
}
else if(root1->val!=root2->val)
{
return false;
}
else
{
int ret1 = _isSymmetric(root1->left, root2->right);
int ret2 = _isSymmetric(root1->right, root2->left);
if(ret1&&ret2)
{
return true;
}
else
{
return false;
}
}
}
bool isSymmetric(struct TreeNode* root)
{
return _isSymmetric(root->left, root->right);
}判断这个树是否为对称二叉树,需要判断它的左右子树是否对称。我们需要两个变量,分别指向左右子树,当第一个变量指向左子树时,第二个变量指向右子树,然后判断它们是否相同。在函数名前加下划线代表这个函数是主调函数的子函数,主调函数调用子函数获得返回值。
八、判断一棵树是否为另一棵树的子树
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p == NULL && q == NULL)
{
return true;
}
else if(p!=NULL && q != NULL)
{
if(p->val != q->val)
{
return false;
}
else
{
int ret1 = isSameTree(p->left,q->left);
int ret2 = isSameTree(p->right,q->right);
if(ret1&&ret2)
{
return true;
}
else
{
return false;
}
}
}
else
{
return false;
}
return true;
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
if(root == NULL)
{
return false;
}
else if(root->val == subRoot->val)
{
int ret3 = isSameTree(root,subRoot);
if(ret3 == 1)
{
return true;
}
}
int ret4 = isSubtree(root->left,subRoot);
int ret5 = isSubtree(root->right, subRoot);
if(ret4||ret5)
{
return true;
}
else
{
return false;
}
return false;
}这个问题我们可以调用我们之前实现过的判断两棵树是否相同函数来实现。主调函数先递归,直到这个节点的值与另一棵树的子树的值相同时,这时主树的子树才有可能与另一棵树相同。这时调用判断两棵树相同函数,判断两棵树是否相同。
九、翻转二叉树
struct TreeNode* invertTree(struct TreeNode* root)
{
struct TreeNode* tmp = NULL;
if (root == NULL)
{
return NULL;
}
else
{
tmp = root->left;
root->left = root->right;
root->right = tmp;
invertTree(root->left);
invertTree(root->right);
}
return root;
}翻转二叉树是将二叉树的左右节点全部互换。
十、使用一个给定的数组构建二叉树
// 通过前序遍历的数组"12400508003600700"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
if (a[(*pi)] == 0)
{
(*pi)++;
return NULL;
}
else
{
BTNode* pnew = CreatBinaryTree(a[(*pi)++]);
pnew->_left = BinaryTreeCreate(a, n, pi);
pnew->_right = BinaryTreeCreate(a, n, pi);
return pnew;
}
}构建二叉树是将数组中的数构成一个二叉树。参数1是数组,参数2是指向数组元素的下标。假设数组中0代表空节点,如果遇到空节点0,就返回空,同时将(*pi)++,使它指向数组中下一个元素。然后开辟一个新节点,同时递归调用子函数,将二叉树的子节点都连接到树上去。
十一、将二叉树中的值放入数组中
void PreOrder(struct TreeNode* root, int* a, int* pi)
{
if(root == NULL)
{
return;
}
else
{
a[(*pi)++] = root->val;
PreOrder(root->left, a, pi);
PreOrder(root->right, a, pi);
}
}
int BinaryTreeSize03(struct TreeNode* root)
{
return root == NULL ? 0 : BinaryTreeSize03(root->left) + BinaryTreeSize03(root->right) + 1;
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
int i = 0;
*returnSize = BinaryTreeSize03(root);
int* a = malloc(sizeof(int) * (*returnSize));
PreOrder(root, a, &i);
return a;
}我们需要先开辟数组,使用求二叉树中节点数量的函数来获得开辟数组的长度,然后通过前序遍历将二叉树中的值都放在数组中。