数据结构系列：“平衡” 二叉树之红黑树

1、前言

在写这篇博客之前，我是犹豫的，因为红黑树有点复杂。但是写完以后，我发现不是这样的，仅仅只是红黑树需要处理的细节较多罢了。在本文中，为了让大家更好地理解红黑树，我首先会介绍 B 树，接着会说明红黑树与 4 阶 B 树的等价性，之后再介绍如何在红黑树上添加删除元素。最后我会说明红黑树的平衡性以及它与 AVL 树之间的性能比较。

2、B 树

本文中对 B 树的讲解为的是后续更好地理解红黑树，因此，这部分只涉及理论知识。

2.1 B 树的基本性质

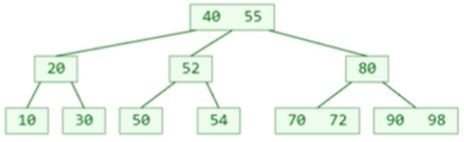
B 树是一类树的总称，我们可以从下面各类 B 树图中看出它们的特点：
（1）它和二叉搜索树很像，也是“左小右大”；
（2）它的每一个节点可以存储不止一个元素，并且每一个节点也可以超过两个分支；
（3）B 树的阶数与它的最大分支树相等；
（4）B 树是一种绝对平衡的树，所谓绝对平衡，是指从根节点到任一叶子节点所经过的节点数量一定是相同的。



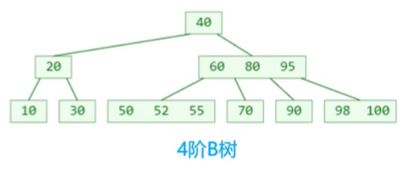
除此以外，B 树与各个节点储存的元素个数有一定的关系。我们假设一棵 B 树的阶数为 m（m >= 2），一个节点存储的元素的个数为 x:
（1）根节点：1 <= x <= m - 1；
（2）非根节点：向上取整(m/2) - 1 <= x <= m - 1；
（3）如果有子节点，子节点个数 y = x + 1；
根据（1）和（2），我们可以得到根节点的子节点个数为：2 <= y <= m;
非根节点的子节点个数为：向上取整(m/2) <= y <= m。

以上的这些性质可以从图中推出来。

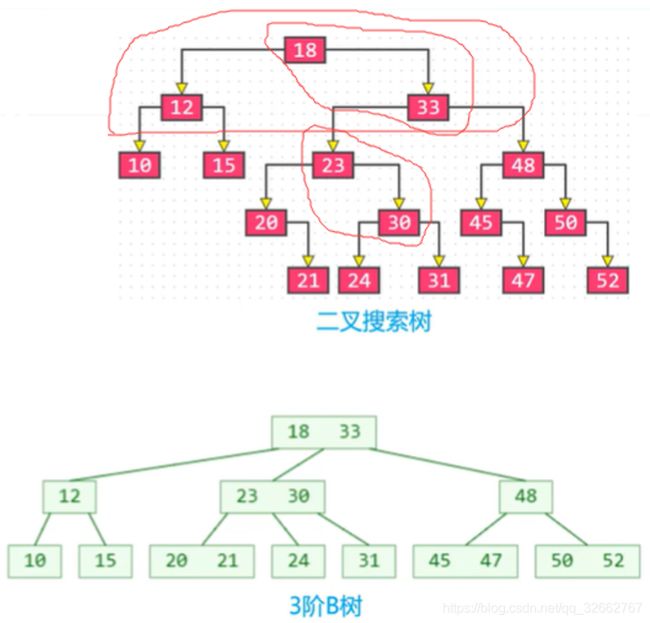
2.2 B 树与二叉搜索树

两者在逻辑上是等价的，如下图。从图中我们可以看出，B 树的节点是由二叉搜索树的多代节点合并而来。

2.3 如何在 B 树上搜索元素

和二叉搜索树一样，若插入节点的元素小的话，则往左孩子方向继续比较，元素大了往右孩子方向继续比较，若碰到一个节点有多个元素，则从小到大比较元素即可。

2.4 如何在 B 树上添加元素

2.4.1 添加元素的各类情况

在 B 树上添加元素和二叉搜索树类似，最终添加的元素会出现在叶子节点。在 B 树上我们要注意一个情况，如 2.1 部分所讲，B 树的根节点和非根节点有对应的元素个数限制。而添加元素有可能会超出这一限制，我们称这一现象为上溢。若上溢发生，我们需要进行对应的处理。下面我们通过一个图例赖展现这一过程：

添加元素之前：

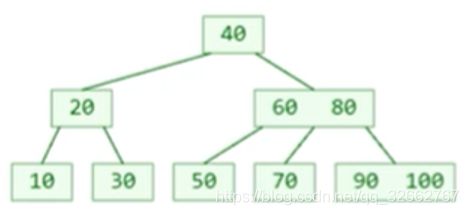
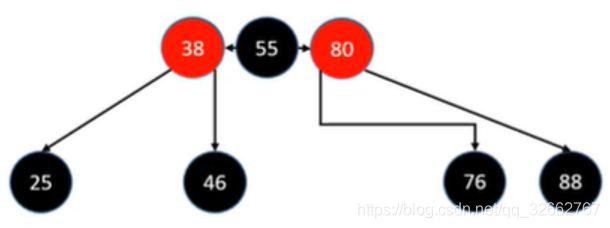
添加元素 55 后（满足 B 树的性质）：

继续添加元素 95 后（上溢）。我们可以看到这是一棵 3 阶 B 树，它的非根节点的元素个数应该在 [1, 2] 之间。而节点 {90， 95， 100} 显然已经不符合性质了。

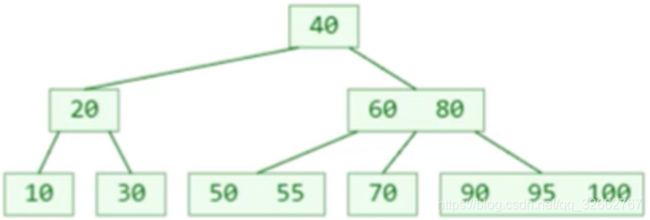
2.4.2 如何处理上溢

如果发生了上溢，此时我们的程序应该及时检测到这类情况。因此，上溢现象一旦发生，该节点的元素个数必定和 B 树的阶数相等，我们假设为 m。

此时，（1）我们将该节点中间元素的位置找出来，我们假设为 k；（2）将这第 k 个元素和该节点的父节点进行合并；（3）在 [0, k-1] 和 [k+1, m] 的元素分别变成该节点的左右子节点；（4）若父节点也溢出，则继续按照（1）（2）（3）（4）的步骤处理。如下图所示，这是一棵 5 阶 B 树插入元素 34 后的情况，图中一共处理了 2 次上溢情况。

2.5 如何在 B 树上删除元素

和在二叉搜索树上删除元素类似，无论删除的是叶子节点还是非叶子节点，最终整棵树删除的还是叶子节点（后者会用左子树中的前驱元素或者右子树中的后继元素来替代）。同时，删除元素也会出现节点元素个数不符合 B 树性质的情况（ 向上取整(m/2) - 1 <= x <= m - 1），我们称之为下溢。

2.5.1 删除节点（无下溢情况）

如下图所示，若删除的元素是叶子节点，直接将该元素摘除即可。若不是，找前驱元素或者后继元素替代即可。

情况 1，删除的是叶子节点。删除元素 30 前：

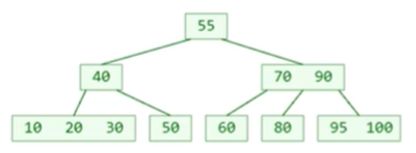
情况 1，删除的是叶子节点。删除元素 30 后：

情况 2，删除的是非叶子节点。删除元素 60 前：

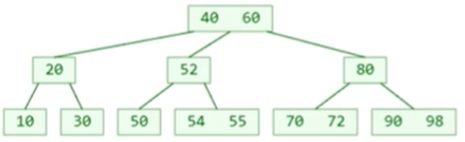
情况 2，删除的是非叶子节点。删除元素 60 后：

2.5.2 删除节点（产生下溢）

如下图所示，假设这是一棵 5 阶 B 树。当我们删除元素 22 后，此时该节点已经不满足 向上取整(m/2) - 1 <= x 这一性质（5 阶 B 树的非根节点的元素个数最少为 2），因此我们需要进行相应的调整。

调整的过程如下：

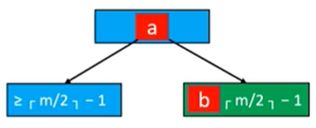
（1）下溢节点的元素个数必然等于向上取整(m/2) - 2。如果兄弟节点的个数大于等于 向上取整(m/2)，我们便可以向兄弟节点借取一个元素。如下图所示，绿色节点为下溢节点，我们可以将父节点元素 b 挪下来，并让元素 a (最大元素) 成为父节点元素，这个过程其实就是 AVL 树中的旋转。

处理前：

处理后：

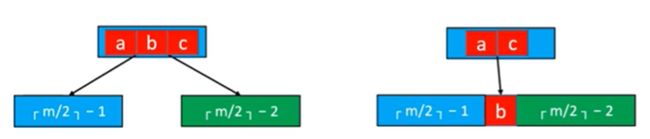
（2）如果此时兄弟节点的元素个数正好等于临界值：向上取整(m/2) - 1，则我们不能借取元素了。此时我们的做法是将父节点中的元素往下挪，与左右子节点合并。此时合并后的节点的元素个数最多为 m - 1，不会发生上溢现象。如下图所示。

3、2-3-4 树与红黑树的等价性

因为 4 阶 B 树的非叶子节点的子节点的个数在 [2, 4] 之间，因此 4 阶 B 树也被叫作 2-3-4 树。依据这个规律，5 阶 B 树我们也可以称为 3-4-5 树。为了向大家说明为何红黑树与 2-3-4 树是等价的，我们先来了解红黑树。

3.1 红黑树的性质

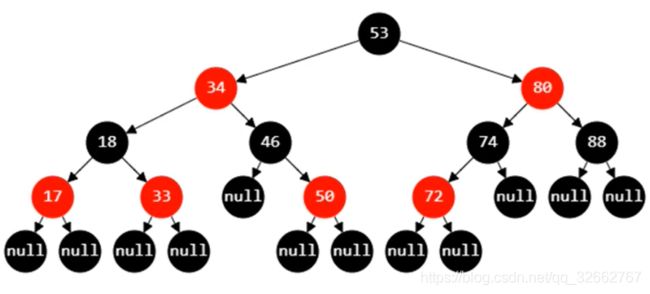
初学者对红黑树这个名字可能会好奇，为什么是叫红黑树（如上图），而不是蓝白树。这和发明创造它的人有关，红色和黑色是为了区分两类不同的节点，以颜色分类可能是为了在视觉上进行区分，就像上图一样。和 AVL 树一样，红黑树本身也是一种自平衡的二叉搜索树，并且必须满足以下五条性质：

（1）红黑树的节点是 RED 或者 BLACK；
（2）根节点必须是 BLACK;
（3）叶子节点都是 BLACK，这里的叶子节点是外部的 null 节点；
（4）RED 节点的子节点都是 BLACK；

• 由（4）我们可以推导出： RED 节点的父节点一定是 BLACK;
• 从根节点到叶子节点的所有路径上不能有 2 个连续的 RED 节点；

（5）从任一节点到所有路径都包含相同数目的 BLACK 节点；

3.2 红黑树与 2-3-4 树的关系（图解）

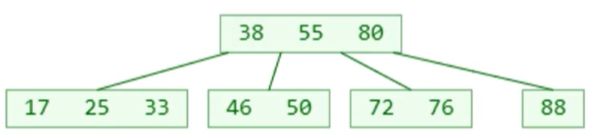
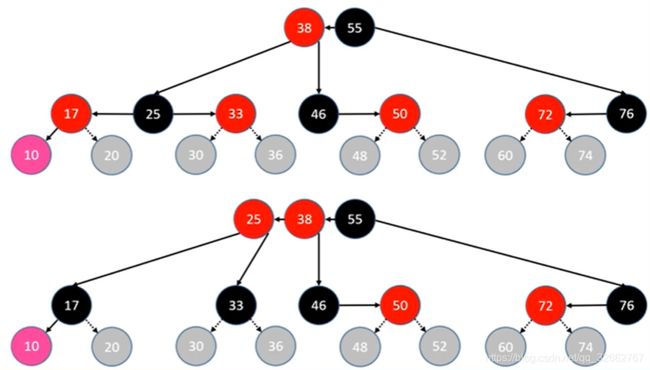
上面是一棵 2-3-4 树，它对应的红黑树是这样的：

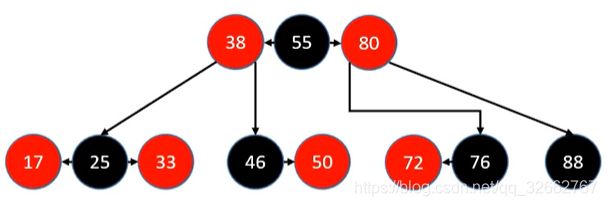
我们将这棵红黑树展开，就变成下面这样：

从上面的图中，我们可以看出红黑树与 2-3-4 树的关系：
（1）2-3-4 树中的节点个数与红黑树中的黑色节点个数相等；
（2）在 2-3-4 树中，一个节点的所有元素对应在红黑树中，只有一个元素是黑节点；反之，红黑树的黑节点与它的红色子节点融合在一起形成 2-3-4 树中的一个节点。

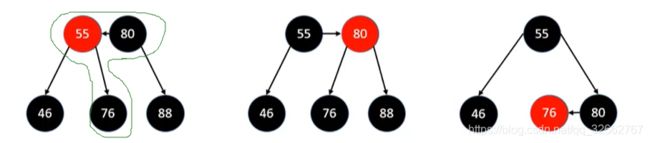
下图是红黑树与 2-3-4 树的对比情况，我们需要牢记的是黑节点会与它的红色子节点融合成一个 B 树节点：

4、红黑树添加元素（代码）

4.1 完成基础代码

在添加元素之前，我们先完成红黑树的基本代码：

首先，红黑树也是一棵二叉搜索树，因此，RBTree 继承 BST：

public class RBTree<E extends comparable> extends BST<E>{
     
	...
	// 构造函数
	public RBTree() {
      }
	public RBTree(Comparator comparator){
     
		this.comparator = comparator;
	}
	...
}

接着，红黑树的节点与先前的节点也有不同，它有一个颜色属性。我们让每一个节点的默认颜色都为红色，因为这样做能尽快地满足红黑树的性质：

（1）红黑树的节点是 RED 或者 BLACK；（默认满足）

（2）根节点必须是 BLACK;（如果添加的节点是第一个节点，直接染黑即可；若不是，则满足）

（3）叶子节点都是 BLACK，这里的叶子节点是外部的 null 节点；（默认满足）

（4）RED 节点的子节点都是 BLACK；（不一定满足，如果红节点的父节点也是红色，则需要进行调整）

• 由（4）我们可以推导出： RED 节点的父节点一定是 BLACK;
• 从根节点到叶子节点的所有路径上不能有 2 个连续的 RED 节点；

（5）从任一节点到所有路径都包含相同数目的 BLACK 节点；（添加红色节点不会影响这条性质，满足）

private static boolean RED = false;
private static boolean BLACK = true;
 
private class RBTree<E> extends Node<E>{
     
	public boolean color = RED;
	
	public RBTree(E element, Node<E> parent){
     
		super(element, parent);
	}
}

在这之后，我们需要一些辅助函数来帮我完成后续的过程：

// 给节点染色
private Node<E> color(Node<E> node, boolean color){
     
	if(node == null){
     
		return node;
	}
	((RBTree)node).color = color;
	return node;
}

// 将节点染成红色
private Node<E> red(Node<E> node){
     
	return color(node, RED);
}

// 将节点染成黑色
private Node<E> black(Node<E> node){
     
	return color(node, BLACK);
}

// 判断节点的颜色
private boolean colorOf(Node<E> node){
     
	if(node == null || node.color == BLACK){
     
		return BLACK;
	}
	((RBTree)node).color = color;
	return node;
}

// 判断节点是否是红色
private boolean isRed(Node<E> node){
     
	return colorOf(node) == RED;
}

// 判断节点是否是黑色
private boolean isBlack(Node<E> node){
     
	return colorOf(node) == BLACK;
}

一如既往的，我们需要 afterAdd 函数与 afterRemove 函数完成添加和删除元素后的调整步骤：

@Override
private void afterAdd(Node<E> node){
     
	...
}

@Override
private void afterRemove(Node<E> node){
     
	...
}

最后，也别忘了 createNode 函数：

@Override
private Node creatNode(Node<E> node, Node<E> parent){
     
	return new RBTree<>(element, parent);	
}

4.2 实现 afterAdd 函数

红黑树添加元素与二叉搜索树并无大的区别，最终被添加的元素依旧是在叶子节点。前面我们提到过新添加的节点默认是红色节点，因此，如果添加的位置不符合红黑树的五条性质，节点本身需要进一步处理。

4.2.1 添加元素的所有情况

下图中的叶子节点涵盖了红黑树的所有情况，一共有 12 种添加的可能。

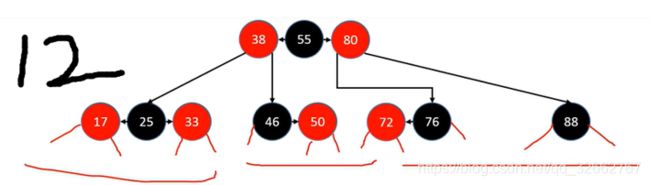
4.2.2 无需做任何处理的情况（4种）

其中，有 4 种添加情况不用做任何处理，如下图所示。这四种情况都是父节点为黑节点，满足红黑树的性质。

4.2.3 需要进一步处理的情况（8种）

还有另外 8 种情况，父节点是红节点，不满足红黑树的性质（不能连续出现两个红节点），这些情况需要做进一步的处理。如下图：

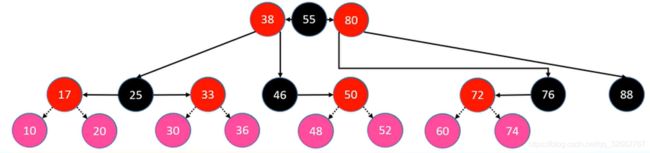
4.2.3.1 uncle 节点不是红色节点

（1）下图是其中的两种情况（图中的灰色节点可以忽略），判定条件是新添加元素的 uncle 节点（父节点的兄弟节点，图中的是 null 节点）不是红色节点。此时我们做两步操作。
A：将 grand 节点（父节点的父节点）染成红色，父节点染成黑色；
B：从 grand 节点开始进行单旋操作（RR，LL）；

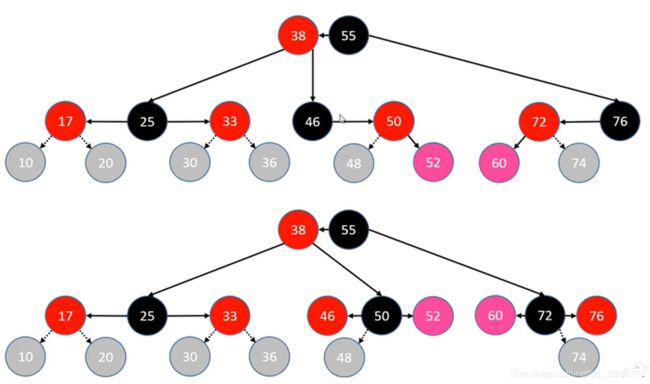
（2）同样的，下图是另外两种情况，和上图不一样的地方在于，图中新添加的节点会形成需要旋转的 RL 和 LR 情况。判定条件依旧是新添加元素的 uncle 节点（父节点的兄弟节点，图中的是 null 节点）不是红色节点。此时我们做两步操作。
A：将 grand 节点（父节点的父节点）染成红色，自身染成黑色；
B：从 grand 节点开始进行双旋操作，RL（parent 右旋转，grand 左旋转），LR（parent 左旋转， grand 右旋转）；

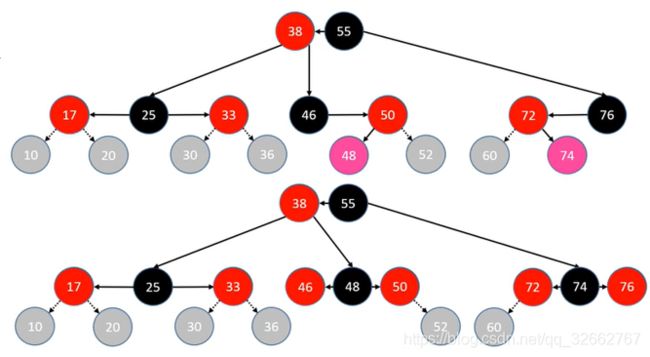
上面我们已经介绍了 4 种添加情况，它们的共同点是新添加节点的 uncle 节点不是红色节点。接下来我们介绍另外 4 种情况，uncle 节点是红色的情况。

4.2.3.1 uncle 节点是红色节点

如下 4 副图，代表了四种不同的添加情况，但它们的处理过程却是相同的。

当我们添加粉红色节点后，叶子节点已经发生了上溢现象（红黑树等价于 4 阶 B 树）。此时我们要考虑的是选择哪个元素与父节点进行合并。为了方便，我们选择新加入节点的 grand 节点向上合并，并且向上合并原色的左右两边元素需要形成新的节点，因此，我们将 parent 节点和 uncle 染成黑色（以 B 树的视角看，一个节点必须有一个黑色节点）。同时，由于 grand 节点往上合并的过程等同于插入新节点的过程，所以我们将它也染成红色。整个过程如下：

A：新节点的 parent、uncle 节点染成黑色；
B：将 grand 节点看成新添加的节点，染成红色，向上合并；
C：合并后依旧可能会发生上溢现象，此时我们可以调用自身进一步处理，整个过程是一个递归的过程，若上溢到根节点，只需要将根节点染成黑色即可；

情况 1：

情况 2：

情况 3：

情况 4：

4.2.4 代码实现

// 获取兄弟节点，此方法应放在 BinaryTree 的 Node 类中
public Node<E> slibing(){
     
	if(isLeftChild()){
     
		return parent.right;
	}
	
	if(isRightChild()){
     
		return parent.left;
	}
	
	return null;
}

private void afterAdd(Node<E> node){
     
	// 首先我们需要获取 parent、uncle 和 grand 节点
	Node<E> parent = node.parent;
	Node<E> uncle = node.slibing();		// slibing 函数获取的是兄弟节点，它的实现放在 BinaryTree 的 Node 类中，实现细节如上所示 
	Node<E> grand = parent.parent;
	
	// 如果新加入的节点是根节点,我们只需要将此节点染黑即可
	if(parent == null){
     
		black(node);
		return;
	}
	
	// 根据我们上面的讨论，添加一共分为 12 种情况，下面我们一一搞定
	// 1、无需进一步调整的情况：父节点是 black 节点。
	if(colorOf(parent) == BLACK){
     
		return;
	}

	// 2、uncle 节点是红色的情况，此时会上溢，需要递归调用此函数做进一步处理
	if(isRed(uncle) == RED){
     
		black(uncle);
		black(parent);
		afterAdd(red(grand));
		return; 
	}

	// 3、uncle 节点不是红色的情况：这里的做法和 AVL 树一样，需要判断是哪种旋转类型，然后根据我们上述的处理步骤进行处理即可。
	if(parent.isLeftChild()){
     	// L-
		if(node.isLeftChild()){
     	// LL
			black(parent);
			red(grand);
			rotateRight(grand);
		}else{
     	// LR
			black(node);
			red(grand);
			rotateLeft(parent);
			rotateRight(grand);
		}
	}else{
     	// R-
		if(node.isLeftChild()){
     	// RL
			black(node);
			red(grand);
			rotateRight(parent);
			rotateLeft(grand);
		}else{
     	// RR
			black(parent);
			red(grand);
			rotateLeft(grand);
		}
	}
}

5、红黑树删除元素（代码）

和二叉搜索树一样，红黑树中最终被删除的元素是叶子节点中的元素（以 B 树的视角看）。因此，删除最终都发生在叶子节点身上。

5.1 删除红色节点

如下两幅图所示，删除红色叶子节点不会改变红黑树的性质。因此，删除后不用进一步做处理。

删除前：

删除后：

5.2 删除黑色节点（一共三种情况）

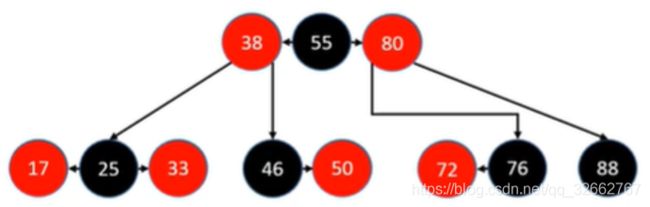
如下图所示，黑色叶子节点一共分为三种情况：

（1）左右有 2 个红色节点（以 B 树的视角来看，图中最左边的叶子节点）；
（2）左右只有 1 个红色节点（以 B 树的视角来看，图中中间两个叶子节点）；
（3）只有黑色节点本身（以 B 树的视角来看，图中最右边的叶子节点）；

5.2.1 删除黑色节点（前两种情况）：如何处理及代码实现

下边我们先讨论前两种情况该如何处理（后一种情况比较多，所以单独拿出来讨论）：

情况（1）：左右有 2 个红色节点；
这种情况下黑色节点被删除，只需要找其中一个红色孩子节点元素替代即可。

情况（2）：左右有 1 个红色节点；
这种情况我们的操作也非常简单，用红色孩子节点代替被删除节点，并将其染黑即可。整个过程如下图所示：

代码实现：

// 这里我们对这个函数的形参做了改动。其中 node 依旧代表的是被删除节点，replacement 是替代节点。这么做是因为在红黑树中，replacement 节点也可能需要做进一步处理，比如染色。

// 由于这个方法也是继承自父类的方法，因此，在整条继承链上的方法也需要做相应形式上的改动。在其他二叉搜索树中，replacement 节点目前用不上，只需要传 null 即可，后序会有进一步的改进。

@Override
private void afterRemove(Node<E> node, Node<E> replacement){
     
	// 如果被删除的节点是红色节点(对应情况 1)，什么都不用做
	if(isRed(node)){
     
		return;
	}

	// 如果被替代节点是红色节点(对应情况 2)，直接染成黑色
	if(isRed(replacement)){
     
		black(replacemnt);
		return;
	}
	...
}

5.2.2 删除黑色节点（最后一种情况）：如何处理

现在要处理的是情况（3）：只有黑色节点本身。

理解这种情况的时候，我们会以 4 阶 B 树的视角看待整个过程。因为叶子节点本身只有一个元素，删除后会产生下溢现象。下面我们分情况讨论如何处理下溢：

（1）只有一个根节点；
这种情况只有直接删除根节点，让 root = null 即可；

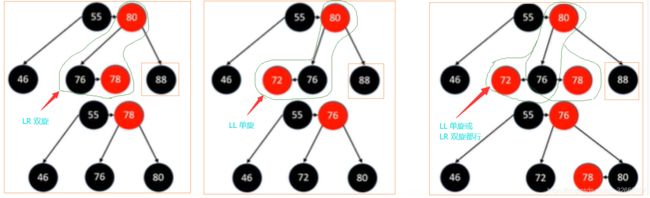
（2）slibing（兄弟）节点至少有一个是 RED 元素。所有的这些情况总结如下图所示（一共 3 种情况），图中被删除的节点是 88，位于 80 的右节点。这种情况的修复过程如下：

A：按照图中所示的情况进行旋转；
B：染色，中心节点继承 parent 的颜色，同时左右子节点染成黑色。

（3）slibing 节点没有一个 RED 节点。

此时我们要做的是让父节点下来合并，这又分为两种情况，父节点是红色与父节点是黑色，对应下图中左右两边的情况：

图中左边的处理：
A：先将 parent 节点染黑；
B：再将 slibing 节点染红；

图中右边的处理：
A：将 slibing 节点染红；
B：这时 parent 节点也出现下溢的情况，我们进一步递归处理 parent 节点便好；

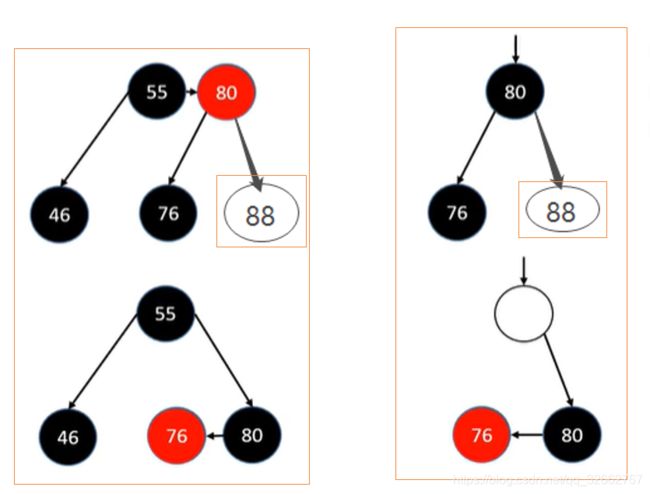
（4）slibing 是 RED 节点。
以 4 阶 B 树的视角来看，这种情况下 slibing 节点是父节点的一份子。处理过程分为以下三个步骤：
A：将 slibing 节点染成黑色，parent 节点染成红色；
B：进行旋转（图中将节点 80 进行右旋转）；
C：这时候又回到 slibing 节点是黑色节点的情况，继续按照（3）中的情况进行处理即可；

5.2.3 删除黑色节点（最后一种情况）：代码实现

按照 5.2.2 部分的介绍，我们需要知道被删除节点的 slibing 节点的颜色，所以我们首先要获取 slibing 节点。

获取 slibing 节点我们本可以直接调用 slibing 函数完成，但是，在 slibing 函数的逻辑中，我们需要知道被删除的 node 节点是左孩子还是右孩子，而在 remove 函数中，我们已经将 parent.left 或 parent.right 清空了（这取决于被删除节点是左孩子还是右孩子），因此，我们可以通过以下逻辑得到 slibing 节点，同时判断被删除的 node 节点是 left 节点还是 right 节点：

	// 首先我们需要判断被删除的节点是左孩子还是右孩子(在上面展示的图中，被删除的节点都是右孩子，也可以是左孩子，两者的区别在于旋转时候的不同)。
	
	boolean left = parent.left == null || parent.isLeftChild();		// 判断被删除节点是左孩子还是右孩子
																	// parent.left == null 是为了判断外面调用 afterRemove 函数的情况
																	// parent.isLeftChild() 是为了判断函数内部调用 afterRemove 函数的情况
																																		
	Node<E> slibing = left ? parent.right : parent.left;	// 获取 slibing 节点

进一步，我们分情况进行讨论。首先我们要先明确被删除的节点是左孩子还是右孩子。两者的处理情况类似，只是在旋转细节上有一些不同，因此，我们完成其中的一个逻辑，另一个套用即可。这里，为了和上述图中的情况对应，我们先完成 else 中的逻辑，大家可以选择先看 else 中的代码和注释。

	if(left){
     	// 如果被删除节点是左孩子，slibing 在右边（完成 else 中的情况，对称处理便好）
		if(isRed(slibing)){
     
			black(sibling);
            red(parent);
            rotateLeft(parent);
            // 更换兄弟
            sibling = parent.right;				
		}
		
		// 能来这里，兄弟节点必然是黑色
		if(isBlack(slibing.left) && isBlack(slibing.right)){
     	// 兄弟节点左右没有一个红色节点
			// 父节点要向下合并
			boolean parentIsBlack = isBlack(parent);
			black(parent);
			red(slibing);
			
			// 合并后，父节点变成黑色。此时，回到了删除单个黑色叶子节点的情况，调用 afterRemove 函数即可
			if(parentIsBlack){
     
				afterRemove(parent, null);
			}
			
		}else{
     		// 兄弟节点中至少有一个是红色节点
			// 在此条件下，一共有 3 种情况需要处理（看上面的图）：兄弟节点有一个红色节点（1 种）或者有两个红色节点（2 种）
			// 为了在代码上实现复用，我们从旋转的角度考虑代码的编写。从图中我们可以知道，有两种情况可以进行 LL 旋转。余下的一种情况需要进行两次旋转，旋转完第一次以后，随后依旧进行 RR 旋转，只是此时的 slibing 节点需要改动。
				
                if(isBlack(sibling.right)){
     		// 兄弟节点的右边是黑色，兄弟要先旋转（余下的一种情况）
                    rotateLeft(sibling);
                    sibling = parent.right;
                }
                
                // 三种情况可以统一处理，RR 情况下都可以进行左旋转
                color(sibling, colorOf(parent));
                black(sibling.right);
                black(parent);
                rotateLeft(parent);
		}
	}else{
     	// 根据上面的图，我们先完成这个逻辑。如果被删除节点是右孩子，slibing 在左边。如果被删除的节点是左孩子，我们只需要将旋转情况颠倒就可以了。
		if(isRed(slibing)){
     
			black(sibling);
            red(parent);
            rotateLeft(parent);
            // 更换兄弟
            sibling = parent.left;				
		}
		
		// 能来这里，兄弟节点必然是黑色
		if(isBlack(slibing.left) && isBlack(slibing.right)){
     	// 兄弟节点左右没有一个红色节点
			// 父节点要向下合并
			boolean parentIsBlack = isBlack(parent);
			black(parent);
			red(slibing);
			
			// 合并后，父节点变成黑色。此时，回到了删除单个黑色叶子节点的情况，调用 afterRemove 函数即可
			if(parentIsBlack){
     
				afterRemove(parent, null);		// 在这种情况下，开始判断是否是 left 节点时需要添加 parent.isLeftChild() 完成逻辑
			}
		}else{
     		// 兄弟节点中至少有一个是红色节点
			// 在此条件下，一共有 3 种情况需要处理（看上面的图）：兄弟节点有一个红色节点（1 种）或者有两个红色节点（2 种）
			// 为了在代码上实现复用，我们从旋转的角度考虑代码的编写。从图中我们可以知道，有两种情况可以进行 LL 旋转。余下的一种情况需要进行两次旋转，旋转完第一次以后，随后依旧进行 LL 旋转，只是此时的 slibing 节点需要改动。
				
                if(isBlack(sibling.left)){
     		// 兄弟节点的左边是黑色，兄弟要先旋转（余下的一种情况）
                    rotateLeft(sibling);
                    sibling = parent.left;
                }
                
                // 这时候·三种情况可以统一处理，LL 情况下都可以进行右旋转
                color(sibling, colorOf(parent));
                black(sibling.left);
                black(parent);
                rotateRight(parent);
		}
	}

6、红黑树的平衡

从 AVL 树的平衡角度看，红黑树并不是一棵严格意义上的平衡二叉树。红黑树中的平衡，是“黑平衡”，即从任一节点到叶子节点所经过的黑色节点是一样多的。它的最大高度是 2log(n)，依旧是 log(n) 级别。

7、AVL 树 VS 红黑树

（1）搜索、添加、删除：两者都是 log(n) 的时间复杂度。

（2）添加和删除后的旋转调整：AVL 树添加元素后需要 O(1) 次旋转，删除元素后需要 O(log(n)) 次旋转；红黑树都只需要 O(1) 次旋转；

在应用中，如果搜索的次数远大于插入和删除，此时 AVL 树更优；搜索、删除、插入次数差不多，选择红黑树。相对于 AVL 树来说，红黑树牺牲了部分平衡性换取插入删除操作时少量的旋转操作，整体上性能要优于 AVL 树。因此，综合增删改查所有操作，红黑树是一种统计性能更优的二叉树。

8、总结

传说中令人闻风丧胆的红黑树都被我搞定了，我还怕啥呢？接下来，我会继续介绍一些更为抽象的数据结构，集合、映射等，敬请期待。