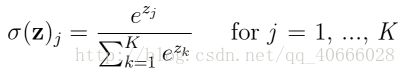TensorFlow入门（3）-单层神经网络实现方法

这里将构建一个简单的线性分类器。

神经网络的组成

神经网络中最常见的运算，就是计算输入、权重和偏差的线性组合。

这里 W 是连接两层的权重矩阵。输出 y，输入 x，偏差 b 全部都是向量。

根据前面学习的用神经网络处理分类问题，需要考虑以下几个方面：

• 数据准备
• 激活函数选择
• 损失函数选择
• 梯度下降法
• 参数选择
• 重复训练

数据准备

上一篇基本概念里面讲到TensorFlow里面的几种常用的运算：tf.constant()、tf.placeholder()、tf.Variable()，会分别设置常量tensor、占位tensor、变量tensor。

当然，这里的数据处理还包括对于输入数据（features）的归一化、二值化、清洗等预处理过程，对标签（labels）进行独热编码（one-hot encoding），略去不讲，这是特征工程的坑，下次再补上。

输入x、输出y
对于不同的数据集可能采用不同的参数，需要的session运行之前，设置输入。因此用tf.placeholder()。

x = tf.placeholder(tf.float32, (None, x_count))
y = tf.placeholder(tf.float32, (None, y_count))

None 维度在这里是一个 batch size 的占位符。在运行时，TensorFlow 会接收任何大于 0 的 batch size。（因为batch中的数据量不同，可能有128组，也可能是100组，下面讲Mini-batch gradient descent会提到）

权重 weight
训练神经网络的目的是更新权重和偏差来更好地预测目标。为了使用权重和偏差，需要一个能修改的 Tensor。因此用tf.Variable()。

w = tf.Variable(tf.truncated_normal((x_count, y_count)))

# 要记得初始化变量
init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)

初始权重的取值有一个简单的通用方法：从高斯分布上随机获取，使权重的均值为0，标准差为σ。
tf.truncated_normal((x_count, y_count)) 返回一个tensor矩阵，维度为x_count * y_count，随机值取自正态分布，并且它们的取值会在这个正态分布平均值的两个标准差之内。（截尾正态分布 tf.truncated_normal）

偏差 bias
和权重一样，偏差也是需要动态修改的，因此也选用tf.Variable()。
因为权重已经被随机化来帮助模型不被卡住，不需要再把偏差随机化了。可以简单地把偏差设为 0。

b = tf.Variable(tf.zeros(y_count))

激活函数

前面的二分类问题中接触过S型函数（sigmoid），S 型函数的导数最大值为 0.25，这意味着，当你用 S 型函数单元进行反向传播时，网络上每层出现的错误至少减少 75%，如果有很多层，权重更新将很小，这些权重需要很长的训练时间。因此，S 型函数不适合作为隐藏单元上的激活函数。

修正线性单元 ReLU
近期的大多数深度学习网络都对隐藏层使用修正线性单元 (ReLU)。如果输入小于 0，修正线性单元的输出是 0，如果输入大于 0，则输出等于输入。
数学表示为：  f(x)=max(x,0) 

ReLU 激活函数是你可以使用的最简单非线性激活函数。当输入是正数时，导数是 1，所以没有 S 型函数的反向传播错误导致的消失效果。

不足
摘自 Andrej Karpathy 的 CS231n 课程：

遗憾的是，ReLU 单元在训练期间可能会很脆弱并且会变得“无效”。例如，流经 ReLU 神经元的大型梯度可能会导致权重按以下方式更新：神经元将再也不会在任何数据点上激活。如果发生这种情况，那么流经该单元的梯度将自此始终为零。也就是说，ReLU 单元会在训练期间变得无效并且不可逆转，因为它们可能会不再位于数据流形上。例如，学习速度（learning rate）设置的太高，你的网络可能有高达 40% 的神经元处于“无效”状态（即神经元在整个训练数据集上从未激活）。如果能正确地设置学习速度，那么该问题就不太容易出现。

隐藏层设置激活函数为ReLU函数的方法：

hidden_layer = tf.nn.relu(hidden_layer)

softmax
可以用于多分类问题，和sigmoid一样将每个单元的输出压缩到0和1之间，但是softmax会使输出之和等于1，其输出显示了任何类别为真的概率。
多分类的问题再输出层会选择softmax函数作为激活函数。数学表达式如下：

输出层设置softmax函数为激活函数的方法：

prediction = tf.nn.softmax(logits)

损失函数

前面接触的一些问题，多采用的方差损失函数（均方误差MSE），比如在二分类问题中，对于单输出和的sigmoid函数适用。
但是当你在使用 softmax 时，输出是向量。一个向量是输出单元的概率值。而标签用的是独热编码（one-hot encoding）的方法，标签元素为1，其他为0。怎么计算预测向量和标签向量？我们希望误差与这些向量之间的距离成比例。

要计算这个距离，需要使用交叉熵，神经网络训练目标将为：通过尽可能地减小交叉熵使预测向量与标签向量尽量靠近。

交叉熵是信息理论中的概念，这里有两篇参考文章比较不错：
- 可视化信息理论，英文原文参考http://colah.github.io/posts/2015-09-Visual-Information/
- 分类问题损失函数的信息论解释

交叉熵等于标签元素的和乘以预测概率的自然对数。注意：该等式并不对称！千万不能交换向量，因为标签向量里有很多 0，对 0 求对数将产生错误。
tensorflow下用法如下：

cross_entropy = -tf.reduce_sum(y * tf.log(prediction), \
                    reduction_indices=1)

梯度下降

先放一篇讲梯度下降优化算法的文章：An overview of gradient descent optimization algorithms

梯度下降是最流行的优化算法之一，且是目前为止最常见的优化神经网络的方法。梯度下降是通过在目标函数梯度相反的方向上更新模型参数，来最小化目标函数（如损失函数），求解全局最小值。

梯度下降有三种变种，批量梯度下降、随机梯度下降和小批量梯度下降，不同之处在于计算目标函数梯度时所用的数据量的多少。

批量梯度下降（Batch gradient descent）
就是普通的梯度下降，利用全部的数据计算目标函数的梯度。计算梯度有一个经验法则，如果计算这个操作需要n次浮点运算，那么计算这个梯度则需要3倍计算量。

每进行一次参数更新需要计算总体训练数据的梯度，如果这个数据集较大，将会是一个非常大的计算量，梯度下降会变得非常慢，而且占用内存大。同时，无法进行在线更新，比方说新的样本不停的到来。

批量梯度下降能保证在目标函数为凸的情况下取得全局最小值，非凸时取得局部最小值。

随机梯度下降（Stochastic gradient descent）
随机梯度下降以一个训练例子和标签进行一次参数更新。SGD速度更快并支持在线学习。

相比于计算整体的损失，SGD直接计算样本的估计值，通过随机抽取很小一部分的平均损失（一般在1个到1000个样本）和导数，假设那个导数就是梯度下降的正确方向，虽然实际上偶尔会增加损失，但是通过每次执行非常非常小的步幅，总的来说非常有效。

SGD在数据和模型尺寸方面扩展性很好。

小批量梯度下降（Mini-batch gradient descent）
综合了上面两个算法的优点，小批量梯度下降是一次训练数据集的一小部分，而不是整个训练集。它可以使内存较小、不能同时训练整个数据集的电脑也可以训练模型。

在每一代（eopchs）训练之前，对数据进行随机混洗，然后创建 mini-batches，对每一个 mini-batch，用梯度下降训练网络权重。因为这些 batches 是随机的，你其实是在对每个 batch 做随机梯度下降（SGD）。

一般mini-batch的规模在50~256之间。

自己实现一个划分batches的函数：

def batches(batch_size, features, labels):
    """
    Create batches of features and labels
    :param batch_size: The batch size
    :param features: List of features
    :param labels: List of labels
    :return: Batches of (Features, Labels)
    """
    assert len(features) == len(labels)
    output_batches = []

    sample_size = len(features)
    for start_i in range(0, sample_size, batch_size):
        end_i = start_i + batch_size
        batch = [features[start_i:end_i], labels[start_i:end_i]]
        output_batches.append(batch)

    return output_batches

# 主函数中的调用如下
for batch_features, batch_labels in batches(batch_size,\
                                                 train_features, train_labels):
    sess.run(optimizer, feed_dict={features: batch_features,\
                                                 labels: batch_labels})

参数选择

SGD的参数超空间：

• 权重初始化参数
  
  • 用方差较小的随机权重进行初始化，如截尾正态分布。（tf.truncated_normal()）
• 学习率参数
  
  • 如果毫无进展，首先尝试降低学习率。
• 学习率衰减
  
  • 步长随着训练的过程越来越小。
• 动量 momentum
  
  • 追踪梯度的实时平均值，用该值代替当前一批数据计算得出的方向，这种动量技术常常有更好的收敛性。
• batch size

另外，ADAGRAD方法是对SGD的改版，自动选择了动量跟学习率衰减，通常会使学习过程对超参数不敏感。adagrad让学习速率自适应参数，对低频参数进行大幅度更新、对高频参数进行小幅度更新。很适合处理稀疏数据（指元素大部分为零的情况，比如在一段视频中进行猫脸识别）。

重复训练

这里用到一个epochs的概念，可以翻译成“代”。是指对整个数据集训练一次，这个参数需要和learning rate结合使用，learning rate低，需要的epochs自然就高一些。

用法也很简单，就是在最外层加一个循环。

epochs = 10       # 根据需要更改
......
with tf.Session() as sess:
    sess.run(init)

    # 循环训练
    for epoch_i in range(epochs):
    ......

---

参考资料
[1] TensorFlow 深度学习笔记 TensorFlow实现与优化深度神经网络
[2] An overview of gradient descent optimization algorithms
[3] TensorFlow 官方文档中文版
[4] 梯度下降优化算法综述（翻译）