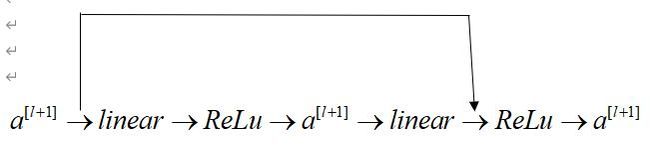(一,4NN-QI)卷积神经网络—吴恩达深度学习课程配套笔记
【第一章】神经网络基础
目录:
- (一,1NN-QI)神经网络与深度学习
- (一、2NN-QI)改善深层神经网络
- (一、3NN-QI)结构化机器学习项目
- ( 一、4NN-QI)卷积神经网络
- (一、5NN-QI)序列模型,循环神经网络
本篇内容为从神经网络基础到量化投资应用的第一章神经网络基础之第四节内容,主要介绍了卷积神经网络,卷积神经网络主要是作用在图片识别中的应用。下面介绍了什么叫卷积、卷积神经网络怎么搭建、卷积神经网络怎么用。
第四节 卷积神经网络
- 目录
- 1.计算机视觉
- 2.深度卷积网络:实例探究
- 3.目标检测
- 4.特殊应用:人脸识别和神经分格转换
1.计算机视觉
深度神经网络最常见的应用就是计算机视觉,比如我们常见的人脸解锁手机,人脸支付等。而计算集视觉最常用的模型为卷积神经网络。
1.1 边缘检测
以人脸识别为例,人脸识别的过程为边缘识别、部位识别、人脸识别。
比如在这样的图片中我们首先寻找栅栏,人体等边缘线。
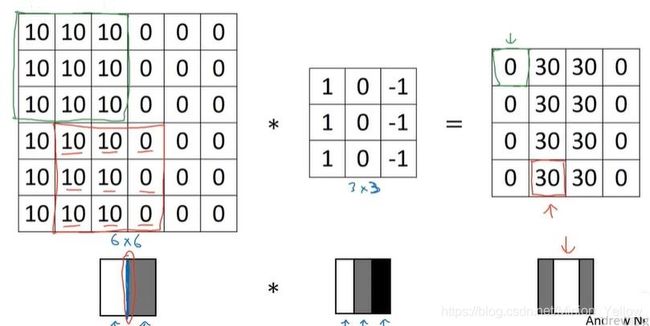
下面我们来看这个过程是怎么实现,假设我们有一张6*6像素的图片,其中每个像素点的值为该点的亮度,通过亮度举证和滤波器做卷积可以得到这个矩阵的边缘矩阵。通过边缘矩阵便可以了解到该图片的边缘。以下述图片为例,卷积运算:即是把用滤波器(蓝色部分)盖住的部分全部和滤波器对应为止相乘,得出边缘举证所对应的第一个值。然后依次平移滤波器从而的得出全部的边缘矩阵的值。
现在以一张黑白图片为例,左半为白色所以亮度值为10,右边为灰色所以亮度值为0,然后通过图中这样的垂直滤波器
经过卷积运算可以得出边缘矩阵,从边缘矩阵中可以看出在图的中间存在着一个边,之所以在边缘矩阵中间的线会显的非常的宽,这是因为我们的图片过于小,只有6*6,而我们通常用手机拍的照片都是几千乘以几千的。
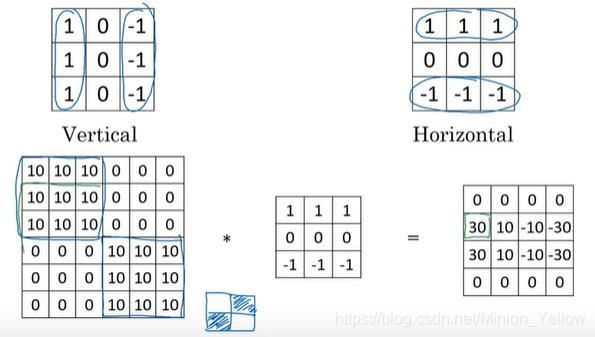
现在我们已经知道了图片中的一个边缘是怎么被电脑发现的,那么我们怎么知道这个边缘是从亮到暗呢,还是从暗到亮呢?————边缘矩阵的正负值,我们通过边缘矩阵值的正负来判断一个边界是从亮到暗还是从暗到亮。举例下面的矩阵在相同滤波器的情况下,第一个图片为从亮到暗,则可得出边缘矩阵为正值,第二个图片为从暗到亮得出边缘矩阵为正值。
前面几个都为垂直滤波器是用来检测图片中的垂直边缘,那么水平的先可以检测吗?当然可以,我们只需要用水平滤波器即可。
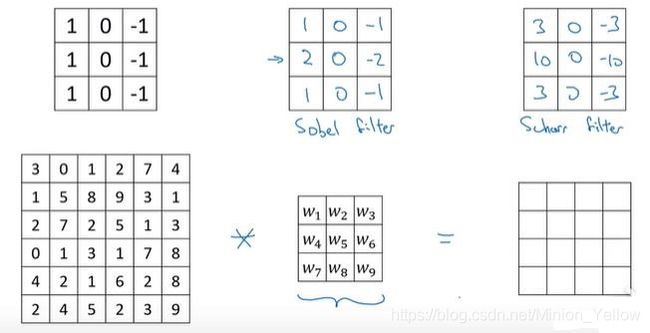
除了垂直滤波器和水平滤波器,还有sobel filter 、 Scharr filter等,各个滤波器之间所不同也就是滤波器当中的参数所不同。通过调节滤波器的参数,我们可以实现图片中所有角度的边缘检测。而且滤波器中的参数我们也可以通过反向传播进行学习(之后的章节会讲到)。
1.2 padding、 卷积步长
1.2.1 padding
通过上面的边缘化过程,我们可以看到一张6*6的图片和一个3*3的滤波器做卷积运算最后得到一个4*4的边缘矩阵。我们把输入的亮度矩阵假设为n*n维的,滤波器为*f*f维的,那么我们最后的边缘矩阵为(n-f+1)*(n-f+1)维。
如果按照这样的计算,经过深层网络,我们的输入图片岂不是要最终变为1*1,所以为这种情况的发生,我们采用padding(池化),计算,即将我们原来的图片向外添加一层为0的像素值。
参数P=padding,上面的扩增p=1,所以输入变为了8*8,滤波器为3*3,则边缘矩阵为(n-f+1)*(n-f+1)=6*6.
卷积层根据是否有Padding(扩张),可以分为两类:
- 1.“Valid”:n✖n * f✖f =n-f+1✖n-f+1
- 2.“Same”:Pad so that output size is the same as the input size.
所以有:
( n + 2 p − f + 1 ) × ( ( n + 2 p − f + 1 ) = n × n 解 得 : P = f − 1 n (n+2p-f+1)\times((n+2p-f+1)=n \times n\\ {}\\ 解得: P=\frac{f-1}{n} (n+2p−f+1)×((n+2p−f+1)=n×n解得:P=nf−1
1.2.2卷积步长(Strided)
在之前用滤波器扫描图像得时候都是每次只平移一步。如果设步长为2,则有:
7 × 7 ∗ 3 × 3 = 3 × 3 P = n u m o f p a d d i n g S = n u m o f s t r i d e n × n ∗ f × f = ⌊ n + 2 P − f S + 1 ⌋ × ⌊ n + 2 P − f S + 1 ⌋ 其 中 ⌊ z ⌋ = f l o o r ( z ) 表 示 向 下 取 整 , 如 果 放 到 图 中 理 解 就 是 , 当 滤 波 器 平 时 的 时 候 只 有 滤 波 器 矩 阵 全 部 在 图 像 当 中 才 进 行 计 算 , 如 果 滤 波 器 有 一 列 超 出 图 像 , 则 不 进 行 计 算 。 7\times 7 * 3\times 3=3\times 3\\ {}\\ P =num \ of \ padding \quad S=num \ of \ stride\\ {}\\ n\times n \ * \ f\times f= \lfloor \frac{n+2P-f}{S} + 1 \rfloor \times \lfloor \frac{n+2P-f}{S} + 1 \rfloor\\ {}\\ 其中\lfloor z \rfloor =floor(z)表示向下取整,如果放到图中理解就是,当滤波器平时的时候只有滤波器矩阵全部在图像当中才进行计算,如果滤波器有一列超出图像,则不进行计算。 7×7∗3×3=3×3P=num of paddingS=num of striden×n ∗ f×f=⌊Sn+2P−f+1⌋×⌊Sn+2P−f+1⌋其中⌊z⌋=floor(z)表示向下取整,如果放到图中理解就是,当滤波器平时的时候只有滤波器矩阵全部在图像当中才进行计算,如果滤波器有一列超出图像,则不进行计算。
在数学当中,卷积运算是需要进行旋转的,而在机器学习当中卷积运算时直接把滤波器对图像进行平行扫描,这种运算在数学当中称之为互相关。但是只有时机器学习领域,卷积运算都表示的是像上述运算一样,不进行镜像映射。这一点在看文献的时候需要注意。
1.2.3 三维卷积
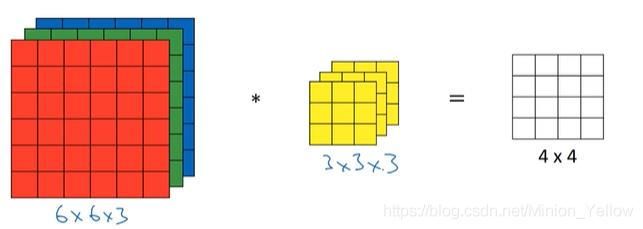
上述图片可以看做是一张黑白图片,因为输入的特征只是一个上面有亮度的矩阵,现在我们来考虑具有RGB格式的图片,每一张图片我们三个维度的特征,那么想对应的滤波器也需要三个维度的滤波器,如果只是考虑红色层面颜色的强度,滤波器的后两层只需要设置为0矩阵即可。但是这里需要注意的是输出维4*4的一维矩阵。其中每一个值是由对应位置的27(3*3*3)个矩阵相乘得到的。
如果对一个RGB图片同时用两个滤波器(一个垂直,一个水平,或其他)做处理,则最后可以得到一个4*4*2的边缘矩阵。
1.3卷积神经网络
上一节我们基本都介绍了在一个深度学习中,一个卷积层的基本框架,现在我们来看一个完成的单层卷积网络是什么样子的。
- 单层卷积网络的工作原理:
z [ 1 ] = w [ 1 ] a [ 0 ] + b [ 1 ] a [ 1 ] = g ( z [ 1 ] ) z^{[1]}=w^{[1]}a^{[0]}+b^{[1]}\\ {}\\ a^{[1]}=g(z^{[1]}) z[1]=w[1]a[0]+b[1]a[1]=g(z[1])
summary of notation:
i f l a y e r 1 i s c o n v o l u t i o n l a y e r : f [ 1 ] = f i l t e r s i z e p [ 1 ] = p a d d i n g s [ l ] = s t r i d e n l [ l ] = n u m b e r o f f i l t e r s I n p u t : n H [ l − 1 ] × n w [ l − 1 ] × n c [ l − 1 ] O u t p u t : n H [ l ] × n w [ l ] × n c [ l ] n H [ l ] = ⌊ n H [ l − 1 ] + 2 p [ l ] − f [ l ] S [ l ] + 2 ⌋ n W [ l ] = ⌊ n W [ l − 1 ] + 2 p [ l ] − f [ l ] S [ l ] + 2 ⌋ A [ l ] = m × n H [ l ] × n w [ l ] × n l [ l ] E a c h f i l t e r i s : f [ l ] × f [ l ] × n c [ l − 1 ] A c t i v a t i o n s : a [ l ] : n H [ l ] × n w [ l ] × n c [ l ] W e i g h t s : f [ l ] × f [ 1 ] × n c [ l − 1 ] × n c [ l − 1 ] b i a s : n c [ l ] if \ layer \ 1 \ is\ convolution \ layer:\\ {}\\ f^{[1]}=filter \ size \\ {}\\ p^{[1]}=padding\\ {}\\ s^{[l]}=stride\\ {}\\ n_l^{[l]}=number \ of \ filters\\ {}\\ Input :\ n_{H}^{[l-1]} \times n_{w}^{[l-1]}\times n_c^{[l-1]}\\ {}\\ Output: n_H^{[l]} \times n_w^{[l]} \times n_c^{[l]}\\ {}\\ n_{H}^{[l]}=\lfloor \frac{n_{H}^{[l-1]}+ 2p^{[l]}-f^{[l]}}{S^{[l]}} +2 \rfloor\\ {}\\ n_{W}^{[l]}=\lfloor \frac{n_{W}^{[l-1]}+ 2p^{[l]}-f^{[l]}}{S^{[l]}} +2 \rfloor\\ {}\\ A^{[l]}=m \times n_H^{[l]} \times n_w^{[l]} \times n_l^{[l]}\\ {}\\ Each filter is: f^{[l]} \times f^{[l]} \times n_c^{[l-1]}\\ {}\\ Activations : a^{[l]} : n_H^{[l]} \times n_w^{[l]} \times n_c^{[l]}\\ {}\\ Weights:f^{[l]} \times f^{[1]} \times n_c^{[l-1]} \times n_c^{[l-1]}\\ {}\\ bias: n_c^{[l]} if layer 1 is convolution layer:f[1]=filter sizep[1]=paddings[l]=stridenl[l]=number of filtersInput: nH[l−1]×nw[l−1]×nc[l−1]Output:nH[l]×nw[l]×nc[l]nH[l]=⌊S[l]nH[l−1]+2p[l]−f[l]+2⌋nW[l]=⌊S[l]nW[l−1]+2p[l]−f[l]+2⌋A[l]=m×nH[l]×nw[l]×nl[l]Eachfilteris:f[l]×f[l]×nc[l−1]Activations:a[l]:nH[l]×nw[l]×nc[l]Weights:f[l]×f[1]×nc[l−1]×nc[l−1]bias:nc[l]
1.3.1简单卷积网络实例
该神经网络是一个含有三个隐藏层的神经网络,第一个隐藏层的滤波器大小维3*3的,共有10个滤波器,第二层的滤波器大小为5*5,共有20个,第三层滤波器的大小为5*5的,共有40个,所以在神经网络的最后一层为softmax函数。通过这个简单的卷积网络,可以实现对图片的识别和分类。
- 卷积神经网络的常用的卷积层为(conv,pool):
- Convlution
- Pooling
- fully connectend
1.3.2 池化层
池化层就是通过滤波器去搜索滤波器范围的最大(中间)值。最常用的池化层为max pooling层。
卷积计算为把所有的值相成,而是去寻找范内的最大值。处理最大池化层,还有均值池化层,但是却不常用。多为池化成和多为卷积层的表述一样,这里就不再赘述。
1.3.3 卷积神经网络示例
如图为两个卷积层两个池化层,两个全连接层构成的,但是在神经网络中,只有存在参数的层,才会计入网络的总层数,所以上述网络可以分为3层神经网络,两层卷积层和一层全链接层。其中个位置的参数值变化如下:
所以这就是一个简单卷积神经网络,之所以卷积神经网络比全连接神经网络在图像识别上做的更好,有两个原因:
- 参数共享
- 稀疏链接
2. 深度卷积网络:实例探究
通过上一小节的学习,我们了解了卷积神经网络的基本组成构建,卷积层、池化层、全连接层等,这一节我们通过学习一些实例来学习卷积网络,常见的卷积网络有:
- Classic networks(经典神经网络)
- LeNet-5
- AlexNet
- VGG
- ResNet(残差神经网络)
- Inception
2.1 经典网络
2.1.1 LeNet-5
LeNet-5,是1998年Lecun发表的一篇论文上面的一种方法,有兴趣的同学可以去读原文:【LeCun et al.,1998.Gradient-based learning applied to document recognition】LeNet-5是一个由两个卷积层,两个池化层,两个全连接层构成。
其中输入层是一个32*32*1的手写数字7,经过6个5*5的滤波器,步长为1进行扫描,得到一个28*28*6的矩阵,然后再经过一个平均池化层,池化层中的滤波器为2*2,步长为2进行pooling,然后得到一个14*14*6的矩阵,再次经过一个卷积层,一个池化层,两个全连接层,最后输出为softmax层,从而完成对输入的分类。
2.1.2 AlexNet
AlexNet神经网络是以作者的名字命名的,如果想更多的了解神经网络,可以去读原文【Krizhevsky et al.,2012.ImageNet classification with deep convolutional neural networks】
- 其主要结构为:
2.1.3 VGG-16
VGG-16具有非常简单的结构,具有卷积层和maxpool层,结构为:CONV=3*3 filter,s=1,same,MAX-POOL=2*2,s=2.在卷积层中滤波器为3*3,扫描步长为1,Padding=same。池化层中的滤波器为Max-POOL大小为2*2,扫描步长为2,其具有简单的结构,但是其是深层网络结构。其中原文为:【Simonyan & Zisserman 2015.Very deep convolutional networks for large-scale image recognition】
- 结构为:
第一个箭头表示一个224*224*3的图片经过3*3的滤波器步长为1扫描,Padding=same,经过两层网络得到一个224*224*64的特征。然后再经过POOL层,卷积层,依次类推。
2.2 ResNets(残差神经网络)
残差链接是通过残差块实现跳跃,建立跳跃链接,从而可以将第一层的信息传递给深层网络…为了避免梯度消失和梯度爆炸。下面我们来看具体的结构。
首先这是一个普通的神经网络。
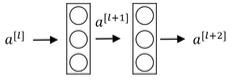
a [ l + 1 ] → l i n e a r → R e L u → a [ l + 1 ] → l i n e a r → R e L u → a [ l + 1 ] 这 是 一 个 不 同 的 两 层 神 经 网 络 , 如 果 用 数 学 公 式 表 示 既 是 : z [ l + 1 ] = W [ l + 1 ] a [ l ] + b [ l + a ] a [ L + 1 ] = g ( z [ l + 1 ] ) z [ l + 2 ] = W [ l + 2 ] a [ l + 1 ] + b [ l + 2 ] a [ l + 2 ] = g ( z [ l + 2 ] ) a^{[l+1]} \rightarrow linear \rightarrow ReLu \rightarrow a^{[l+1]} \rightarrow linear \rightarrow ReLu \rightarrow a^{[l+1]}\\ {}\\ 这是一个不同的两层神经网络,如果用数学公式表示既是:\\ {}\\ z^{[l+1]}=W^{[l+1]}a^{[l]}+b^{[l+a]}\\ {}\\ a^{[L+1]}=g(z^{[l+1]})\\ {}\\ z^{[l+2]}=W^{[l+2]}a^{[l+1]}+b^{[l+2]}\\ {}\\ a^{[l+2]}=g(z^{[l+2]}) a[l+1]→linear→ReLu→a[l+1]→linear→ReLu→a[l+1]这是一个不同的两层神经网络,如果用数学公式表示既是:z[l+1]=W[l+1]a[l]+b[l+a]a[L+1]=g(z[l+1])z[l+2]=W[l+2]a[l+1]+b[l+2]a[l+2]=g(z[l+2])
所以由跳跃的方式,我们可以将a[l+1]直接跳到最后线性层之后。
a [ l + 2 ] = g ( z [ l + 1 ] + a [ l ] ) a^{[l+2]}=g(z^{[l+1]}+a^{[l]}) a[l+2]=g(z[l+1]+a[l])
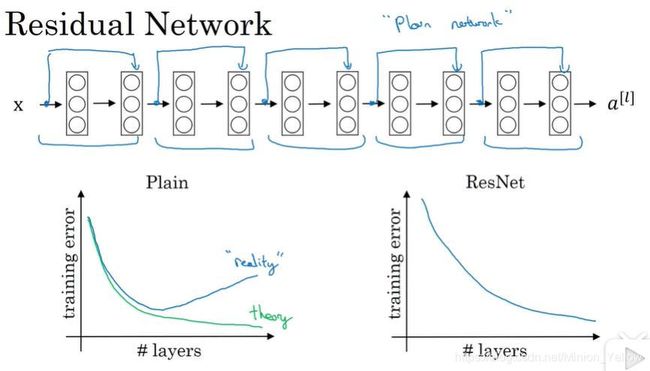
在普通的神经网络中,随着深度的加深,训练误差先是不断的降低,然后再次上升,这是由于随着网络深度的加深其错误也会越来越多。残差神经网络可以避免这个问题。
下面我们来理解一下为什么,残差神经网络有助于提高深度神经网络的效率:
假 设 激 活 函 数 为 R e L u , a ≥ 0 a [ l + 2 ] = g ( z [ l + 2 ] + a [ l ] ) = g ( w [ l + 2 ] a [ l + 1 ] + b [ l + 2 ] + a [ l ] ) i f W [ l + 2 ] = 0 , b [ l + 2 ] = 0 则 g ( a [ l ] ) = a [ l ] 假设激活函数为ReLu,a \geq0\\ {}\\ a^{[l+2]}=g(z^{[l+2]}+a^{[l]})\\ {}\\ =g(w^{[l+2]}a^{[l+1]}+b^{[l+2]}+a^{[l]})\\ {}\\ if \ W^{[l+2]}=0,b^{[l+2]}=0\\ {}\\ 则g(a^{[l]})=a^{[l]} 假设激活函数为ReLu,a≥0a[l+2]=g(z[l+2]+a[l])=g(w[l+2]a[l+1]+b[l+2]+a[l])if W[l+2]=0,b[l+2]=0则g(a[l])=a[l]
由公式是可以发现,只要我们设置w和b都为0,那么a[l+2]=a[l],那么这两层网络将不起作用,如果是一个普通的深度神经网络学习一个简单的函数,也需要经过过度的学习,从而导致发生错误,而残差网络可是使得网络“该简单的时候简单,该复杂的时候复杂”。所以可以提高深度神经网络的效率。
2.3 Inception网络
2.3.1 网络中的网络以及1x1卷积
假设滤波器为一个1x1的矩阵,如果输入特征为一个nxnx1的矩阵,相当于给这个矩阵乘以数倍,但是输入矩阵是高维的是时候,相当于对输入矩阵进行切片,然后进行特征提取。
2.3.2 谷歌Inception网络简介
当我们不知道滤波器应该选则多大,是否需池化的时候,Inception则是一个不错的选择,Inception网络可以通过学习帮助我们选择上面的这些参数。
- Inception结构
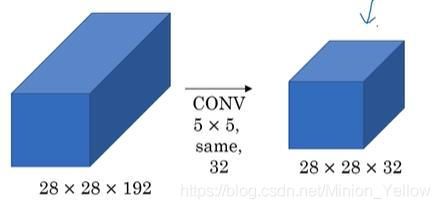
通过上述的结构可以看的这样做会增加整体网络的计算成本,我们以5X5的滤波器来计算一下计算成本。
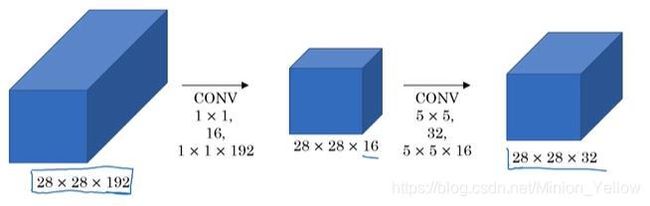
输入层是一个28*28*192的特征,滤波器为5*5*192大小的,共有32个滤波器,那么总需要计算量为:28*28*32*5*5*192=120M.1.2亿的计算量既是对于现在的计算仍然也是一个巨大的计算量。
现在我们通过1x1卷积,来同样完成上述过程:
输入仍然为28x28x192,输出为28x28x32,第一层,使用的滤波器为1x1x192的,共16个,所以第一层的计算量为:28x28x192x16=2.4M,第二层使用的滤波器的大小为5x5x16,一共32个滤波器,所以计算量为28x28x16x5x5x32=10M,所以两层的计算量共为12.4M,相比上一种方法计算量缩小了10倍。在该种计算方法当中可以看到1x1的卷积层最小,可以当做是算法的瓶颈。
构建自己的Inception网络
前面我们已经了解了Inception的基本模块,现在我们来构建自己的Inception网络。
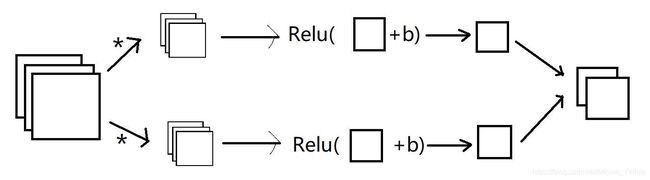
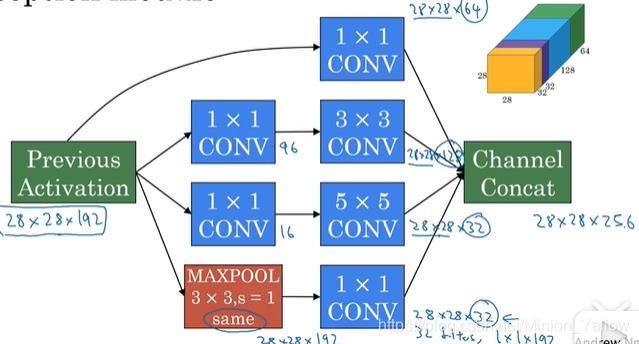
- Inception module
由图可以看出Inception模块的作用就是把不同大小滤波器的卷积层和池化层进行结合起来,而Inception网络就是将这些模块组合起来。
[Szegedy et al,.2014,Going Deeper with Convolutions]
2.4 关于卷积网络的实用性建议
1.多使用开源性代码
可以到GitHub使用开源性代码来实现自己的工作。
2.迁移学习
在深度学习领域,有的网络需要巨大的训练集和多个GPU的运算,这个时候我们可以把别人已经训练好的网络和权重下载下来,只把最后的几层,或者最后的输出层替换为自己的输出层,从而可以使用别人训练好的网络来完成自己的任务。这就是迁移学习,通过自己拥有的数据量,自己决定迁移的部分。
假如我们有两只宠物猫,一只叫Tigger,一只叫Mity,现在想创建一个网络,用以识别我们自己的两只宠物猫。这个时候我们可以使用迁移学习,通过训练把最后的输出层换为softmax函数用于完成自己的项目。
3.数据扩充
计算机视觉主要处理的数据是像素值,通常数据集越大对网路的训练越好,所以计算机视觉方面数据集的增强是非常有必要的。通常数据的扩增方法有:
- 物理扩充
- Rotation
- Shearing
- Local warping
- ……
- 色彩转变
3. 目标检测
3.1目标定位
这一节我们来学习目标定位,在图像识别的过程种,我们不仅需要识别出图片种物体的信息,而且还需要识别出该物体在图片中的相对位置,比如在自动驾驶的应用当中,应该从图片中识别出车辆、行人、交通灯和它们的相对位置。
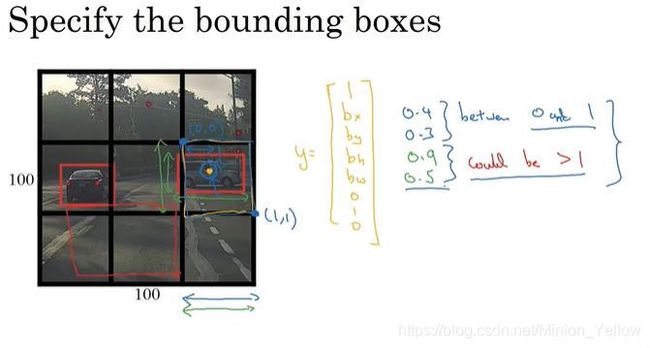
那么在神经网络当中,输入一张图片的时候,我们的输出不仅仅有softmax分类,而且还应该标标注出该物体的大小和相对位置。我们用bx,by,bh,bw表示,(bx,by)表示物体在图片中的相对位置,(bh,bw)表示该物体的大小。
- Notation
现 在 我 们 来 描 述 一 下 本 节 内 容 所 使 用 的 标 记 , 以 自 动 驾 驶 为 例 , 假 设 我 们 需 要 识 别 出 的 标 记 有 : 1. P e d e s t r i a n 2. c a r 3. m o t o r c y c l e 4. b a c k g r o u n d 定 义 目 标 值 y : y = { P c b x b y b h b w c 1 c 2 c 3 } 其 中 P c 用 来 标 记 图 片 中 是 否 还 有 物 体 , ( 0 、 1 ) 0 表 示 该 图 片 只 是 一 张 ( b a c k g r o u n d ) , 此 时 其 他 的 参 数 将 没 有 意 义 。 1 则 表 示 该 图 片 时 包 含 有 其 他 的 物 体 , c 1 , c 2 , 3 分 别 表 示 是 否 含 有 行 人 ( p e d e s t r i a n ) , 汽 车 ( c a r ) 、 摩 托 车 ( m o t o r c y c l e ) 。 b x , b y , b h , b w 分 别 表 示 该 物 体 的 位 置 和 大 小 。 那 么 此 时 的 代 价 函 数 为 : L ( y ^ , y ) = { ( y ^ 1 − y 1 ) 2 + y ^ 2 − y 2 ) 2 + … … y ^ r − y r ) 2 i f y 1 = 1 ( y ^ 1 − y 1 ) 2 i f y 1 = 0 现在我们来描述一下本节内容所使用的标记,以自动驾驶为例,假设我们需要识别出的标记有:\\ {}\\ 1.Pedestrian\\ {}\\ 2.car\\ {}\\ 3.motorcycle\\ {}\\ 4.background\\ {}\\ 定义目标值y:\\ {}\\ y = \left\{ \begin{matrix} P_c\\ b_x\\b_y\\b_h\\b_w\\c_1\\c_2\\c_3 \end{matrix} \right\} {}\\ 其中P_c用来标记图片中是否还有物体,(0、1)0表示该图片只是一张(background),此时其他的参数将没有意义。1则表示该图片时包含有其他的物体,c_1,c_2,_3分别表示是否含有行人(pedestrian),汽车(car)、摩托车(motorcycle)。b_x,b_y,b_h,b_w分别表示该物体的位置和大小。\\ {}\\ 那么此时的代价函数为:\\ {}\\ L(\hat{y},y)= \left\{ \begin{aligned} & (\hat{y}_1-y_1)^2+\hat{y}_2-y_2)^2+……\hat{y}_r-y_r)^2 \quad if \ y_1=1\\ & (\hat{y}_1-y_1)^2 \quad if \ y_1=0\\ \end{aligned} \right. 现在我们来描述一下本节内容所使用的标记,以自动驾驶为例,假设我们需要识别出的标记有:1.Pedestrian2.car3.motorcycle4.background定义目标值y:y=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧Pcbxbybhbwc1c2c3⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫其中Pc用来标记图片中是否还有物体,(0、1)0表示该图片只是一张(background),此时其他的参数将没有意义。1则表示该图片时包含有其他的物体,c1,c2,3分别表示是否含有行人(pedestrian),汽车(car)、摩托车(motorcycle)。bx,by,bh,bw分别表示该物体的位置和大小。那么此时的代价函数为:L(y^,y)={ (y^1−y1)2+y^2−y2)2+……y^r−yr)2if y1=1(y^1−y1)2if y1=0
3.1.1 特征点检测
我们检测一个物体的位置和特征,是通过图片中的特征点来实现,比如在人脸识别中,我们可以通过定义左眼角,内眼角,外眼角,右眼角的特征点,来判断眼睛的位置,通过在嘴上的特征点来判断是微笑还是伤心。例如一张人脸上标记64个特征点,那么神经网络将输出129个点,64*2+1=129,第一个特征为0-1标记,标记图片中是否包含人脸。
3.1.2 目标检测
具体怎么实现目标检测,仍然以自动驾驶为例,首先输入一些汽车占整个图片大部分的图片,训练一个分类神经网络,判断一个图片是否有汽车,再通过滑动窗口实现对一张图片中汽车的定位。
首先用一个较小的窗口以一定的步长遍历整个图片,对每个小窗口进行卷积神经网络判断,判断每个小的窗口是否包含汽车,然后再换用较大的窗口进行遍历,从而实现对整个图片的检测,发现图片的位置和大小。
3.1.3 卷积的滑动窗口实现
1.全连接层转为卷积层
为了实现滑动窗口,我们将最后的全连接层,通过使用和输入一样大的滤波器,实现将全连接层替换为卷积层。
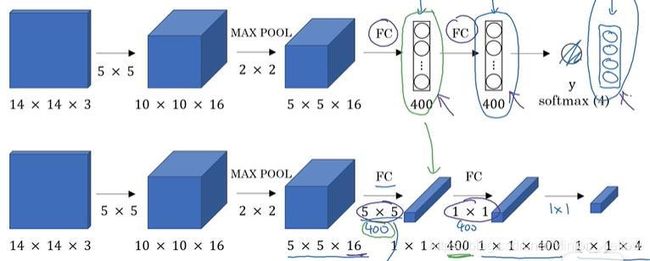
在上一节中我们了解到对如果对一个图片进行卷积神经网络的检测,则需要把这个图片分成许多小块,分别输入到神经网络当中,完成分类。但是这样做的缺点显而易见,增加了计算成本。现在我们通过将全连接层换为卷积层,从而完成对图片的分类。原文参见【Sermanet et al.,2014,OverFeat:intrgrated recognition, Iocalization and detection using convolutional networks】
如图所示,卷积神经网络通过14*14*3的图片训练得来得,现在测试集是16*16*3的图片,那么如果用14*14拆剪一共需要拆为4块,但是由图上可以看出利用卷积层代替全连接层得出一个4*4的矩阵,这样只需要一次计算便可以完成4次“切割”的运算。当处理28*28的图片时类似。
3.1.4 Bounding Box预测
通过上面的算法我们可以大致发现物体的位置,但是并不能精确的找到物体的边界。现在我们介绍一种算法YoLo算法。原文参见【Redom et al.,2015,You Only Look Once: Unified real-time object detection】
原理既是先把图片分为九宫格和形式,例如图中分为3*3大小的图片分别对9个格子,每一个进行卷积神经网络进行判断,只把包含物体中心点的格子看作是一包含物体的格子,然后通过格子的相对位置给出物体的大小和坐标。
3.2 算法检测
3.2.1交并比
搭建好自己的对象定位网络后,怎么判断自己的算法的精确度?我们通过交并比函数来判断算法的精确度。
- 交并比函数(loU,Intersection over union)
l o U = s i z e o f I n t e r s e c t i o n s i z e o f U n i o n loU=\frac{size \ of \ Intersection }{size \ of \ Union} loU=size of Unionsize of Intersection
通常我们认为大于0.5即位测试成共。
3.2.2非极大值抑制
当我们的图片被分为许多小格子的时候,当我们进行loU算法的时候可能会出现多个格子都有输入的情况,这个时候我们采用非极大值抑制法,即调亮loU值最大的情况,抑制loU值最低的格子。
3.2.3 Anchor Boxes
上面的情况都是一个格子中包含一个物体,如果一个格子中包含两个物体那么应该怎么处理,引入Anchor Boxes。
首先人工定义两个Anchor box1 和 Anchor box2。然后通过对分析出来的连个形状和 box1和box2 做对比分别划入对应的输出。当我们没有引进Anchor box时,输出为3*3*8,引入Anchor box 时,输出为3*3*3*16.
3.2.4 YoLo算法
原文:【Redmon et al.,2015,You Only Look Once: Unified real-time object detection】
4. 特殊应用:人脸识别和神经分格转换
4.1 人脸识别系统
4.1.1 One-shot learning
在人脸识别项目中,如果使用人脸图片作为训练集,我们会出现训练集过少,因为在系统中,可能只会保存每个人的一张图片,但是在深度学习中,少量的数据不可能训练出强健的神经网络,而且如果有新加入的成员,那么我们就需要重新学习一个网络,这样的成不是巨大而且也不适合应用。
现在为了解决上述问题,我们采用similarity函数,similarity函数用于比较两张图片的相似度,当我们有一个输入,比较输入图片和系统内已经存在图片,然后输出两个图片的相似度。
- similarity函数
d ( i m g 1 , i m g 2 ) = d e g r e e o f d i f f e r e n c e b e t w e e n i m a g e i f d ( i m g 1 , i m g 2 ) ≤ τ " s a m e " > τ " d i f f e r e n t " d(img1,img2)=degree of difference between image\\ {}\\ \begin{aligned} if \ d(img1,img2) &\leq \tau \quad "same"\\ & > \tau \quad "different" \end{aligned} d(img1,img2)=degreeofdifferencebetweenimageif d(img1,img2)≤τ"same">τ"different"
所以我们只需要去学习similarity函数即可。
4.1.2 Siamese network
学习similarity函数使用的就是Siamese network.[Taigman et. al., 2014 DeepFace closing the gap to human level performance]
- Siamese network
Siamese network主要工作就是将图片x1输入卷积神经网络当中得出一个特征向量f(x1),然后将x2输入相同的卷积神经网络,得出特征向量f(x2),通过定义f(x1)和f(x2)函数的二范数比较x1和x2的相似度。
d ( x ( 1 ) , x ( 2 ) ) = ∣ ∣ f ( x ( 1 ) ) − f ( 2 ) ∣ ∣ 2 2 d(x^{(1)},x^{(2)})=||f(x^{(1)})-f^{(2)}||^2_2 d(x(1),x(2))=∣∣f(x(1))−f(2)∣∣22
所以接下来需要做的就是通过反向传播实现参数的学习
Parameters of NN define an encoding f(x^i):
Learn parameters so that:
If xi,xj are the same person,d is small,
If xi,xj are different person,d is large.
4.1.3 Triplet 损失
现在我们需要建立一个三元损失函数,然后通过反向传播实现参数得学习。
原文参见:【Schroff et al.,2015,FaceNet:A unified embedding for face recognition and clustering】
上 图 中 有 三 张 图 片 , 其 中 左 边 的 两 张 为 同 一 个 人 , 右 边 的 两 个 为 不 同 的 两 个 人 , 因 此 左 边 的 距 离 函 数 会 小 于 右 边 的 距 离 函 数 。 w a n t : ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 + α ≤ ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 − ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 + α ≤ 0 其 中 α , 是 为 了 防 止 f ( i m a g e ) = 0 的 情 况 , 如 果 f ( i m a g e ) = 0 , 那 么 将 出 现 ∣ ∣ 0 − 0 ∣ ∣ − ∣ ∣ 0 − 0 ∣ ∣ = 0 在 这 种 情 况 下 即 使 不 相 同 的 图 片 也 会 出 现 相 减 得 0 的 情 形 。 L o s s f u n c t i o n L ( A , P , N ) = m a x ( ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 − ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 + α , 0 ) J = ∑ i = 1 m L ( A ( i ) , P ( i ) , N ( i ) ) 所 以 上 述 函 数 为 一 个 三 元 损 失 函 数 , 通 过 选 取 数 据 组 A , P , N 来 训 练 。 我 在 选 取 这 些 数 据 组 的 时 候 , 应 随 机 的 选 取 一 些 难 训 练 数 据 组 , 这 样 可 以 不 仅 可 以 提 高 网 络 学 习 的 效 率 , 也 可 以 提 出 学 习 的 精 度 。 所 以 应 该 遵 循 原 则 : d ( A , P ) + α ≈ d ( A , N ) 上图中有三张图片,其中左边的两张为同一个人,右边的两个为不同的两个人,因此左边的距离函数会小于右边的距离函数。\\ {}\\ want: \ ||f(A)-f(P)||^2+\alpha \leq ||f(A)-f(N)||^2\\ {}\\ ||f(A)-f(P)||^2- ||f(A)-f(N)||^2 +\alpha \leq 0\\ {}\\ 其中\alpha,是为了防止f(image)=0的情况,如果f(image)=0,那么将出现\\ {}\\ ||0-0||-||0-0||=0\\ {}\\ 在这种情况下即使不相同的图片也会出现相减得0的情形。\\ {}\\ Loss \ function\\ {}\\ L(A,P,N)=max(||f(A)-f(P)||^2-||f(A)-f(N)||^2+\alpha,0)\\ {}\\ J=\sum^m_{i=1}L(A^{(i)},P^{(i)},N^{(i)})\\ {}\\ 所以上述函数为一个三元损失函数,通过选取数据组A,P,N来训练。我在选取这些数据组的时候,应随机的选取一些难训练数据组,\\这样可以不仅可以提高网络学习的效率,也可以提出学习的精度。所以应该遵循原则:\\ {}\\ d(A,P)+\alpha \approx d(A,N)\\ 上图中有三张图片,其中左边的两张为同一个人,右边的两个为不同的两个人,因此左边的距离函数会小于右边的距离函数。want: ∣∣f(A)−f(P)∣∣2+α≤∣∣f(A)−f(N)∣∣2∣∣f(A)−f(P)∣∣2−∣∣f(A)−f(N)∣∣2+α≤0其中α,是为了防止f(image)=0的情况,如果f(image)=0,那么将出现∣∣0−0∣∣−∣∣0−0∣∣=0在这种情况下即使不相同的图片也会出现相减得0的情形。Loss functionL(A,P,N)=max(∣∣f(A)−f(P)∣∣2−∣∣f(A)−f(N)∣∣2+α,0)J=i=1∑mL(A(i),P(i),N(i))所以上述函数为一个三元损失函数,通过选取数据组A,P,N来训练。我在选取这些数据组的时候,应随机的选取一些难训练数据组,这样可以不仅可以提高网络学习的效率,也可以提出学习的精度。所以应该遵循原则:d(A,P)+α≈d(A,N)
4.1.4 面部验证与二分类
现在用另外一种方法来学习网络的参数,我们把人脸识别看作是一种二分类算法,输入为两张图片,如果两张图片中是一个人那么则输出1,不是一个人则输出0.原文参见:【Taigman et. al.,2014. DeepFace closing the gap to human level performance】
输 入 为 两 张 图 片 的 特 征 , 中 间 的 网 络 为 S i a m e s e 网 络 , 最 后 的 输 出 层 为 σ 输 出 层 . 定 义 输 出 层 的 σ 函 数 为 : y ^ = σ ( ∑ k = 1 128 w i ∣ f ( x k ( i ) ) − f ( x k ( j ) ) ∣ + b ) 其 中 的 绝 对 值 部 分 也 可 以 换 为 : ( f ( x ( i ) ) k − f ( x ( j ) ) k ) 2 f ( x ( i ) ) k − f ( x ( j ) ) k 输入为两张图片的特征,中间的网络为Siamese网络,最后的输出层为\sigma 输出层.\\ {}\\ 定义输出层的\sigma 函数为:\\ {}\\ \hat{y}=\sigma(\sum^{128}_{k=1}w_i|f(x^{(i)}_k)-f(x^{(j)}_k)|+b)\\ {}\\ 其中的绝对值部分也可以换为:\\ {}\\ \frac{(f(x^{(i)})_k-f(x^{(j)})_k)^2}{f(x^{(i)})_k-f(x^{(j)})_k} 输入为两张图片的特征,中间的网络为Siamese网络,最后的输出层为σ输出层.定义输出层的σ函数为:y^=σ(k=1∑128wi∣f(xk(i))−f(xk(j))∣+b)其中的绝对值部分也可以换为:f(x(i))k−f(x(j))k(f(x(i))k−f(x(j))k)2
4.2 神经风格转换
由图片可以看出,c表示图片的内容,s表示图片的分格,G表示图片c按照分格s的样子进行转换后的样子。这样模型在神经网络中称为神经分格转换。
要构建神经网络转换,需要通过构建代价函数(cost function):
我 们 的 目 标 是 通 过 c 和 s 生 成 G : 定 义 代 价 函 数 ( c o s t f u n c t i o n ) : 代 价 函 数 分 为 了 内 容 代 价 函 数 和 分 格 代 价 函 数 。 J ( G ) = α J c o n t a n t ( C , G ) + β J s t y l e ( S , G ) 定 义 内 容 代 价 函 数 : 内 容 代 价 函 数 的 主 要 思 想 为 : S a y y o u u s e h i d d e n l a y e r l t o c o m p u t e c o n t e n t c o s t . U s e p r e − t r a i n e d C o n v N e t . ( E . g . , V G G n e t w o r k ) L e t a [ l ] ( C ) a n d a [ l ] ( G ) b e t h e a c t i v a t i o n o f l a y e r l o n t h e i m a g e s I f a [ l ] ( C ) a n d a [ l ] ( G ) a r e s i m i l a r , b o t h i m a g e s h a v e s i m i l a r c o n t e n t . J c o n t a n t ( C , G ) = 1 2 ∣ ∣ a [ l ] ( c ) − a [ l ] ( G ) ∣ ∣ 2 我们的目标是通过c和s生成G:\\ {}\\ 定义代价函数(cost function):代价函数分为了内容代价函数和分格代价函数。\\ {}\\ J(G)=\alpha J_{contant}(C,G)+ \beta J_{style}(S,G)\\ {}\\ 定义内容代价函数:\\ 内容代价函数的主要思想为:\\ {}\\ Say \ you \ use \ hidden \ layer \ l \ to \ compute \ content cost. \\ {}\\ Use \ pre-trained \ ConvNet.(E.g.,VGG network)\\ {}\\ Let \ a^{[l](C)} \ and \ a^{[l](G)} \ be \ the \ activation \ of \ layer \ l \ on \ the \ images\\ {}\\ If \ a^{[l](C)} \ and a^{[l](G)} \ are \ similar, \ both \ images \ have \ similar \ content.\\ {}\\ J_{contant}(C,G)=\frac{1}{2}||a^{[l](c)}-a^{[l](G)}||^2\\ {}\\ 我们的目标是通过c和s生成G:定义代价函数(costfunction):代价函数分为了内容代价函数和分格代价函数。J(G)=αJcontant(C,G)+βJstyle(S,G)定义内容代价函数:内容代价函数的主要思想为:Say you use hidden layer l to compute contentcost.Use pre−trained ConvNet.(E.g.,VGGnetwork)Let a[l](C) and a[l](G) be the activation of layer l on the imagesIf a[l](C) anda[l](G) are similar, both images have similar content.Jcontant(C,G)=21∣∣a[l](c)−a[l](G)∣∣2
- 风格代价函数
原文【Gatys et al.,2015. A neural algorithm of aristic style】
定义风格代价函数,首先需要了解什么是图片的分格,在深度学习中我们使用中间层的不同通道的激活项的差异表示图片的分格。例如隐藏层中不同通道展开,如图中第一行的第二部分垂直橘黄和第二行第一部分的橘黄色块分格类似,说明他们的激活项类似。所以通过激活项定义风格矩阵。

S t y l e m a t r i x : L e t a i , j , k [ l ] = a c t i v a t i o n a t ( i , j , k ) . G [ l ] i s n c [ l ] × n c [ l ] 其 中 i 表 示 H i g h t 的 位 置 , j 表 示 w e i g h t 的 位 置 , k 表 示 不 同 的 通 道 。 a 表 示 对 应 位 置 的 激 活 项 . G 表 示 风 格 矩 阵 。 G k k ′ [ l ] ( s ) = ∑ i = 1 n H [ l ] ∑ j = 1 n w [ l ] a i j k [ l ] ( s ) a i j k ′ [ l ] ( s ) 风 格 图 片 的 风 格 G k k ′ [ l ] ( G ) = ∑ i = 1 n H [ l ] ∑ j = 1 n w [ l ] a i j k [ l ] ( G ) a i j k ′ [ l ] ( G ) 生 成 图 片 的 风 格 J s t y l e [ l ] ( S , G ) = 1 ( 2 n H [ l ] n W [ l ] n C [ l ] ) 2 ∑ k ∑ k ′ ( G k k ′ [ l ] ( s ) − G k k ′ [ l ] ( G ) ) J s t y l e ( S , G ) = ∑ l λ [ l ] J s t y l e [ l ] ( S , G ) J ( G ) = α J c o n s t a n t ( C , G ) + β J s t y l e ( S , G ) Style \ matrix:\\ {}\\ Let \ a^{[l]}_{i,j,k}=activation \ at \ (i,j,k).\ G^{[l]} \ is \ n_c^{[l]} \times n_c^{[l]}\\ {}\\ 其中i表示Hight的位置,j表示weight的位置,k表示不同的通道。a表示对应位置的激活项.G表示风格矩阵。\\ {}\\ G^{[l](s)}_{kk'}=\sum_{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_w^{[l]}}a_{ijk}^{[l](s)}a_{ijk'}^{[l](s)} 风格图片的风格\\ {}\\ G^{[l](G)}_{kk'}=\sum_{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_w^{[l]}}a_{ijk}^{[l](G)}a_{ijk'}^{[l](G)} \ 生成图片的风格\\ {}\\ J^{[l]}_{style}(S,G)=\frac{1}{(2n_H^{[l]}n_W^{[l]}n_C^{[l]})^2}\sum_k \sum_{k'}(G_{kk'}^{[l](s)}-G_{kk'}^{[l](G)})\\ {}\\ J_{style}(S,G)=\sum_l \lambda^{[l]} J_{style}^{[l]}(S,G)\\ {}\\ J(G)=\alpha J_{constant}(C,G)+\beta J_{style}(S,G) Style matrix:Let ai,j,k[l]=activation at (i,j,k). G[l] is nc[l]×nc[l]其中i表示Hight的位置,j表示weight的位置,k表示不同的通道。a表示对应位置的激活项.G表示风格矩阵。Gkk′[l](s)=i=1∑nH[l]j=1∑nw[l]aijk[l](s)aijk′[l](s)风格图片的风格Gkk′[l](G)=i=1∑nH[l]j=1∑nw[l]aijk[l](G)aijk′[l](G) 生成图片的风格Jstyle[l](S,G)=(2nH[l]nW[l]nC[l])21k∑k′∑(Gkk′[l](s)−Gkk′[l](G))Jstyle(S,G)=l∑λ[l]Jstyle[l](S,G)J(G)=αJconstant(C,G)+βJstyle(S,G)
总结
这篇笔记主要就是通过截屏吴恩达老师的PPT完成的,哈哈,虽然是在B站上白瞟的,但是感谢吴恩达教授,和up主。卷积神经网络,主要用在图像处理方面,分别讲了卷积神经网络需要构成的各个组件,卷积,padding,池化层,全连接层等。然后通过这些组件构建了经典网络和残差网络,网络的优化方法。第三部分主要讲了对目标的识别。第四部分以人脸识别为例,进一步深入理解了卷积神经网络。其实主要的结构就是理论、例子,理论、例子的结构。可能在学习的过程中会有好多不明白的,但是我希望不要放弃,坚持到最后就会发现前面好多不明白的自然也就明白了。把主要的思想方法理解后,以后进行代码的系统学习就会快的多。有兴趣的同学可以私信,一起交流,,,,