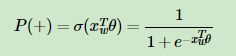word2vec原理(二):基于Hierarchical Softmax的模型
在word2vec原理(一) CBOW与Skip-Gram模型基础中,说到了使用神经网络的方法来得到词向量语言模型的原理和一些问题,现在开始关注word2vec的语言模型如何改进传统的神经网络的方法。由于word2vec有两种改进方法,一种是基于Hierarchical Softmax的,另一种是基于Negative Sampling的。本文关注于基于Hierarchical Softmax的改进方法,在下一篇讨论基于Negative Sampling的改进方法。
1. 基于Hierarchical Softmax的模型概述
先回顾下传统的神经网络词向量语言模型,里面一般有三层,输入层(词向量),隐藏层和输出层(softmax层)。其最大的问题在于从隐藏层到输出的softmax层的计算量很大,因为要计算所有词的softmax概率,再去找概率最大的值。这个模型如下图所示。其中V是词汇表的大小。
![]()
word2vec对这个模型做了改进:
(1)首先,对于从输入层到隐藏层的映射,没有采取神经网络的线性变换加激活函数的方法,而是采用简单的对所有输入词向量求和并取平均的方法。比如输入的是三个4维词向量:(1,2,3,4),(9,6,11,8),(5,10,7,12),那么我们word2vec映射后的词向量就是(5,6,7,8)。这里是从多个词向量变成了一个词向量。
(2)第二个改进,是从隐藏层到输出的softmax层的计算量。为了避免要计算所有词的softmax概率,word2vec采用了霍夫曼树来代替从隐藏层到输出softmax层的映射。如何映射呢?
由于输出softmax层的概率计算变成了一棵二叉霍夫曼树,那么我们的softmax概率计算只需要沿着树形结构进行就可以了。如下图所示,我们可以沿着霍夫曼树从根节点一直走到我们的叶子节点的词w。
![]()
和之前的神经网络语言模型相比,霍夫曼树的所有内部节点就类似之前神经网络隐藏层的神经元,其中,根节点的词向量对应我们映射后的词向量,而所有叶子节点就类似于之前神经网络softmax输出层的神经元,叶子节点的个数就是词汇表的大小。在霍夫曼树中,隐藏层到输出层的softmax映射不是一下子完成的,而是沿着霍夫曼树一步步完成的,因此这种softmax取名为"Hierarchical Softmax"。
如何“沿着霍夫曼树一步步完成”呢?在word2vec中,我们采用了二元逻辑回归的方法,即:(1)规定沿着左子树走,那么就是负类(霍夫曼树编码1);(2)沿着右子树走,那么就是正类(霍夫曼树编码0)。判别正类和负类的方法是使用sigmoid函数,即:
其中![]() 是当前内部节点的词向量,而θ则是我们需要从训练样本求出的逻辑回归的模型参数。
是当前内部节点的词向量,而θ则是我们需要从训练样本求出的逻辑回归的模型参数。
使用霍夫曼树有什么好处呢?(1)首先,由于是二叉树,之前计算量为V,现在变成了log2V;(2)第二,由于使用霍夫曼树,高频的词靠近树根,这样高频词需要更少的时间会被找到,这符合我们的贪心优化思想。
如何分配左右子树呢?依据内部节点的逻辑回归值(即概率)来分配为左右子树。容易理解,被划分为左子树而成为负类的概率为 P(−)=1−P(+)。在某一个内部节点,要判断是沿左子树还是右子树走的标准就是看P(−)、P(+)谁的概率值大。而控制谁的概率值大的因素一个是当前节点的词向量,另一个是当前节点的模型参数θ。
对于上图中的![]() ,如果它是一个训练样本的输出,那么我们期望对于里面的隐藏节点
,如果它是一个训练样本的输出,那么我们期望对于里面的隐藏节点![]() 的P(−)概率大,
的P(−)概率大,![]() 的P(−)P(−)概率大,
的P(−)P(−)概率大,![]() 的P(+)P概率大。
的P(+)P概率大。
回到基于Hierarchical Softmax的word2vec本身,我们的目标就是找到合适的所有节点的词向量和所有内部节点θ, 使训练样本达到最大似然。那么如何达到最大似然呢?
2. 基于Hierarchical Softmax的模型梯度计算
我们使用最大似然法来寻找所有节点的词向量和所有内部节点θ。先拿上面的![]() 例子来看,我们期望最大化下面的似然函数:
例子来看,我们期望最大化下面的似然函数:
![]()
对于所有的训练样本,我们期望最大化所有样本的似然函数乘积。(公式有个错误处:应该是![]() )
)
为了便于我们后面一般化的描述,我们定义输入的词为w:
![]() :输入词
:输入词![]() 从输入层词向量求和平均后的霍夫曼树根节点词向量
从输入层词向量求和平均后的霍夫曼树根节点词向量
![]() :从根节点到w所在的叶子节点,包含的节点总数
:从根节点到w所在的叶子节点,包含的节点总数
![]() :w在霍夫曼树中从根节点开始,经过的第i个节点表示为
:w在霍夫曼树中从根节点开始,经过的第i个节点表示为![]() ,
,
![]() :对应的霍夫曼编码为
:对应的霍夫曼编码为![]() ∈{0,1},其中i=2,3,...
∈{0,1},其中i=2,3,...![]() 。
。
![]() :该节点对应的模型参数表示为
:该节点对应的模型参数表示为![]() , 其中i=1,2,...
, 其中i=1,2,...![]() −1,没有i=
−1,没有i=![]() 是因为模型参数仅仅针对于霍夫曼树的内部节点。
是因为模型参数仅仅针对于霍夫曼树的内部节点。
定义![]() 经过的霍夫曼树某一个节点j的逻辑回归概率为P(dwj|xw,θwj−1),其表达式为:
经过的霍夫曼树某一个节点j的逻辑回归概率为P(dwj|xw,θwj−1),其表达式为:
![]()
那么对于某一个目标输出词![]() ,其最大似然为:
,其最大似然为:
![]()
在word2vec中,由于使用的是随机梯度上升法(因为结果输出为最大概率的词),所以并没有把所有样本的似然乘起来得到真正的训练集最大似然,仅仅每次只用一个样本更新梯度,这样做的目的是减少梯度计算量。这样我们可以得到![]() 的对数似然函数L如下:
的对数似然函数L如下:
![]()
要得到模型中![]() 词向量和内部节点的模型参数θ, 我们使用梯度上升法即可。首先我们求模型参数
词向量和内部节点的模型参数θ, 我们使用梯度上升法即可。首先我们求模型参数![]() 的梯度:
的梯度:
![]()
同样的方法,可以求出![]() 的梯度表达式如下:
的梯度表达式如下:
![]()
有了梯度表达式,我们就可以用梯度上升法进行迭代一步步的求解我们需要的所有的![]() 和
和![]() 。
。
所以,word2vec 使用Hierarchical Softmax对CBOW和Skip-Gram损失结构进行了改进,同时,又利用负采样方式,改进了模型训练。
3. 基于Hierarchical Softmax的CBOW模型
4. 基于Hierarchical Softmax的Skip-Gram模型
5. Hierarchical Softmax的模型源码和算法的对应
这里给出上面算法和word2vec源码中的变量对应关系。
在源代码中,基于Hierarchical Softmax的CBOW模型算法在435-463行,基于Hierarchical Softmax的Skip-Gram的模型算法在495-519行。大家可以对着源代码再深入研究下算法。
在源代码中,neule对应我们上面的e, syn0对应我们的![]() , syn1对应我们的
, syn1对应我们的![]() , layer1_size对应词向量的维度,window对应
, layer1_size对应词向量的维度,window对应![]() 。
。
另外,vocab[word].code[d]指的是,当前单词word的第d个编码,编码不含Root结点。vocab[word].point[d]指的是,当前单词word,第d个编码下,前置的结点。