数据预处理--01 缺失值处理\异常值处理

数据预处理

数据常见的预处理方法 （缺失值处理, 异常值剔除，归一化，离散化 等）
这一篇文章主要介绍缺失值处理\异常值处理 主要是因为他们有比较相似的处理流程.

缺失值处理

包括记录缺失\字段信息缺失, 对数据分析有较大的影响, 导致不确定性增加.
选用哪种方法需要较多的实践经验.
缺失值处理方法:
删除记录\数据插补\不处理

01 判定是否有缺失值 .isnull() .notnull()

s = pd.Series([12,33,45,23,np.nan,np.nan,66,54,np.nan,99])
df = pd.DataFrame({
     'value1':[12,33,45,23,np.nan,np.nan,66,54,np.nan,99,190],
                  'value2':['a','b','c','d','e',np.nan,np.nan,'f','g',np.nan,'g']})
# 判定是否有缺失值, 返回True  False
print(s.isnull())
print(df.isnull())
print(df["value2"].isnull())

如果要知道有多少条数据是有null值的
df["value2"].isnull().sum()  返回True的求和
如果要查询所有列的缺失值情况
df.isnull().sum() 会得到每一列缺失值的总数

02 筛选非缺失值

# 查看缺失项  意义不大
print(df[df["value1"].isnull()])

# 筛选非缺失值 用的比较多
print(df[df["value1"].notnull()])
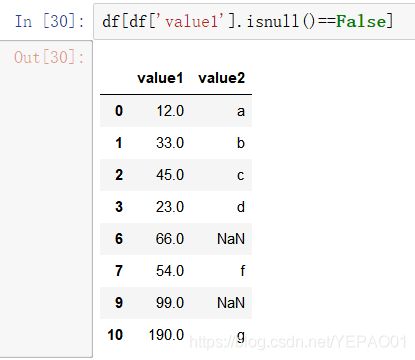
print(df[df["value1"].isnull()==False])

03 删除缺失值 dropna

可用于Series DataFrame, 存在inplace参数, 为True的话, 改变自身值.

s = pd.Series([12,33,45,23,np.nan,np.nan,66,54,np.nan,99])
df = pd.DataFrame({
     'value1':[12,33,45,23,np.nan,np.nan,66,54,np.nan,99,190],
                  'value2':['a','b','c','d','e',np.nan,np.nan,'f','g',np.nan,'g']})
s.dropna()
df.dropna() #两列的null值都被删除 返回两列值
df["value1"].dropna()  #删除"value1"的null值,返回1列值

# 可以通过subset参数来删除在age和sex中含有空数据的全部行
df4 = df4.dropna(subset=["age", "sex"])

04 填充\替换缺失值 .fillna() .replace()

s.fillna(value=None, method=None, axis=None, inplace=False, limit=None, downcast=None, **kwargs)
value：填充值
method参数：
pad / ffill → 用之前的数据填充
backfill / bfill → 用之后的数据填充
注意inplace参数 是否替换原始值

s = pd.Series([12,33,45,23,np.nan,np.nan,66,54,np.nan,99])
df = pd.DataFrame({
     'value1':[12,33,45,23,np.nan,np.nan,66,54,np.nan,99,190],
                  'value2':['a','b','c','d','e',np.nan,np.nan,'f','g',np.nan,'g']})
# 使用0填充
s.fillna(0,replace=True)
df.fillna(0,replace=True)
# 使用之前\之后的值填充 method
s.fillna(method="ffill",inplace=True)
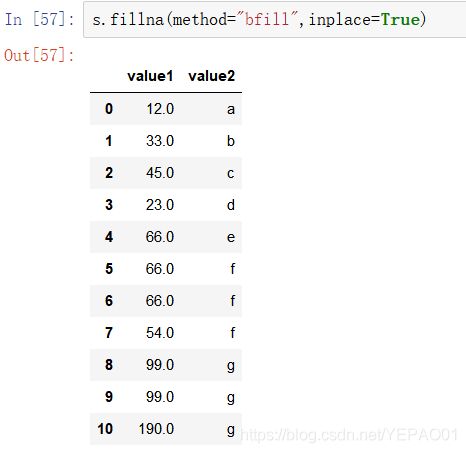
df.fillna(method="bfill",inplace=True)

填充0的截图

填充前\后值的截图

使用replace 替换
df.replace(to_replace=None, value=None, inplace=False, limit=None, regex=False, method=‘pad’, axis=None)
to_replace → 被替换的值
value → 替换值

s = pd.Series([12,33,45,23,np.nan,np.nan,66,54,np.nan,99])
df = pd.DataFrame({
     'value1':[12,33,45,23,np.nan,np.nan,66,54,np.nan,99,190],
                  'value2':['a','b','c','d','e',np.nan,np.nan,'f','g',np.nan,'g']})
s.replace(np.nan,"缺失的值")

05 缺失值插补(3个思路)

思路: 均值\中位数\众数插补, 临近值插补, 插值法
0501 均值\中位数\众数插补

s = pd.Series([1,2,3,np.nan,3,4,5,5,5,5,np.nan,np.nan,6,6,7,12,2,np.nan,3,3])
print("均值:{}".format(s.mean()))
print("中位数:{}".format(s.median()))
print("众数:{}".format(s.mode().tolist()))
s.fillna(s.median(),inplace=True)
s

0502 临近值插补
详见上文 使用replace 替换

0503 插值法–拉格朗日插值法
数学原理:

使用scipy包, 使用已知值生成多项式

# 代码辅助理解
from scipy.interpolate import lagrange
x = [3,6,9,12]
y = [10,8,4,2]
print(lagrange(x,y))
print("当x=2, y={}".format(lagrange(x,y)(2)))

# 代码演示实际应用

异常值处理

异常值是指样本中的个别值, 其数值明显偏离其余的观测值.
异常值也称离群点, 异常值的分析也称为离群点的分析.

异常值分析 → 3σ原则 / 箱型图分析
异常值处理方法 → 删除 / 修正填补

异常值分析及处理(3σ原则\箱型图分析)

优先使用箱型图
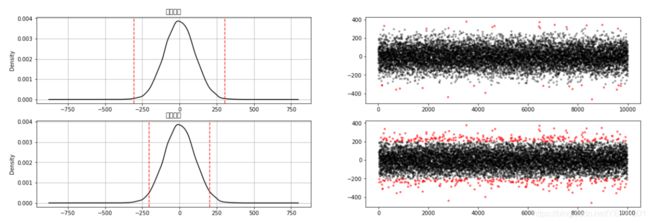
3σ原则
σ是标准差, 3σ原则是指如果数据服从正态分布, 异常值被定义为一组测定值中与平均值的偏差超过3倍的值 --> p(|x-μ| > 3σ) <= 0.003
1 需要首先计算 均值\标准差, 判定是否服从正态分布
2 根据公式 (|x-μ| > 3σ) 是异常值, 得到非异常值
3 图表表达

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
% matplotlib inline
#创建数据
data = pd.Series(np.random.randn(10000)*100)
u = data.mean()
std = data.std()
print("u,std:{}".format((u,std)))
#正态性检验, 返回统计量D的值,P值; 
#D的值越接近0就越表明数据和标准正态分布拟合得越好，
#如果P值>指定水平(5%),不拒绝原假设，可以认为样本数据服从给定分布，否则接受备择假设
stats.kstest(data,"norm",(u,std))

# 建立画布
fig = plt.figure(figsize = (20,10)) #画布的大小
ax1 = fig.add_subplot(3,2,1) #添加图表 (总行数,纵列数,所在位置)
data.plot(kind="kde", grid=True, style="-k",title="密度曲线")
plt.axvline(3*std,hold=None, color="r", linestyle="--", alpha=0.8)
plt.axvline(-3*std,hold=None, color="r", linestyle="--", alpha=0.8)

error = data[np.abs(data-u) > 3*std] #检测异常值
data_c = data[np.abs(data-u) <= 3*std]
print("异常值的条数:{}".format(len(error))
ax2 = fig.add_subplot(3,2,2)
plt.scatter(data_c.index,data_c,color="k", marker=".", alpha=0.3)
plt.scatter(error.index,error,color="r", marker=".", alpha=0.5)

ax3 = fig.add_subplot(3,2,3)
data.plot(kind="kde", grid=True, style="-k",title="密度曲线")
plt.axvline(2*std,hold=None, color="r", linestyle="--", alpha=0.8)
plt.axvline(-2*std,hold=None, color="r", linestyle="--", alpha=0.8)
error = data[np.abs(data-u) > 2*std]
data_c = data[np.abs(data-u) <= 2*std]

error = data[np.abs(data-u) > 2*std]
data_c = data[np.abs(data-u) <= 2*std]
ax4 = fig.add_subplot(3,2,4)
plt.scatter(data_c.index,data_c,color="k", marker=".", alpha=0.3)
plt.scatter(error.index,error,color="r", marker=".", alpha=0.5)

箱型图分析
1 箱型图看数据分布情况
2 查看基本统计量, 计算分位差
3 筛选出error值, 剔除error值
4 图表表达

# 1 箱型图
fig = plt.figure(figsize = (10,6))
ax1 = fig.add_subplot(2,1,1)
color = dict(boxes='DarkGreen', whiskers='DarkOrange', medians='DarkBlue', caps='Gray')
data.plot.box(vert=False, grid = True,color = color,ax = ax1,label = '样本数据')

# 2 查看基本统计量, 计算分位差
s = data.describe()
print(s)
q1 = s['25%']
q3 = s['75%']
iqr = q3 -q1
mi = q1-1.5*iqr
ma = q3+1.5*iqr
print("分位差:{:.3f}, 上限:{:.3f}, 下限:{:.3f}".format(iqr,ma,mi))

# 3 筛选出error值, 剔除error值 
error = data[(data<mi) | (data>ma)]
data_c = data[(data>=mi) & (data<=ma)]
ax2 = fig.add_subplot(2,1,2)
plt.scatter(data_c.index, data_c, color="k", marker=".", alpha=0.3)
plt.scatter(error.index, error, color="r", marker=".", alpha=0.6)
plt.xlim([-10,10010]) # 设置x轴的区间范围
plt.grid() # 添加网格线