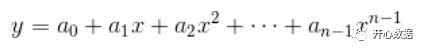eviews如何处理缺失数据填补_python数据预处理之异常值、缺失值处理方法
一、异常值
异常值是指样本中的个别值,其数值明显偏离其余的观测值。异常值也称离群点,异常值的分析也称为离群点的分析。
常用的异常值分析方法为3σ原则、箱型图分析、机器学习算法检测,一般情况下对异常值的处理都是删除和修正填补,即默认为异常值对整个项目的作用不大,只有当我们的目的是要求准确找出离群点,并对离群点进行分析时有必要用到机器学习算法,其他情况下不用费精力去分析他们,今天不讨论基于机器学习算法的离群点检测和分析,改天单独出一个。
1、3σ原则
如果数据服从正态分布,异常值被定义为一组测定值中与平均值的偏差超过3倍的值 → p(|x - μ| > 3σ) ≤ 0.003
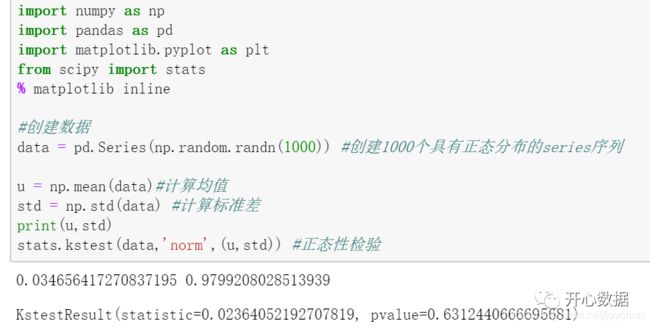
首先创建数据
对数据进行正态性检验,p值为0.63,远远大于 0.05,认为服从正态分布。
接下来绘图查看数据和异常值
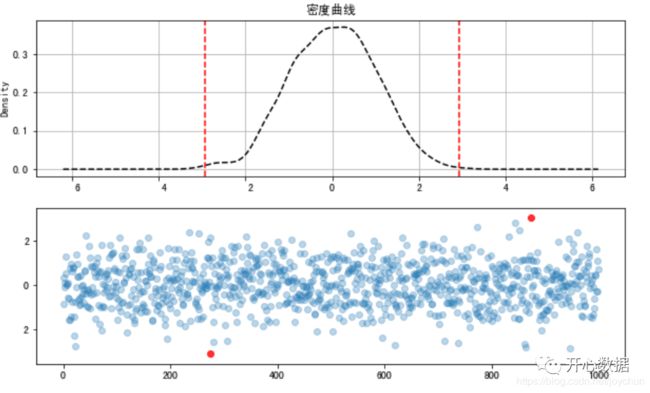
#绘制数据密度曲线fig= plt.figure(figsize=(10,6))ax1=fig.add_subplot(2,1,1)data.plot(kind='kde',style='--k',grid=True,title='密度曲线')plt.axvline(3*std,hold=None,linestyle='--',color='r')plt.axvline(-3*std,hold=None,linestyle='--',color='r') #筛选出异常值和正常值error = data[np.abs(data - u) > 3*std]data_c = data[np.abs(data - u) <= 3*std]ax2=fig.add_subplot(2,1,2)plt.scatter(data_c.index,data_c,alpha=0.3)plt.scatter(error.index,error,color='r',marker='o',alpha=0.8)图中可以看出数据服从标准正态分布,且存在两个异常值
2、箱型图分析
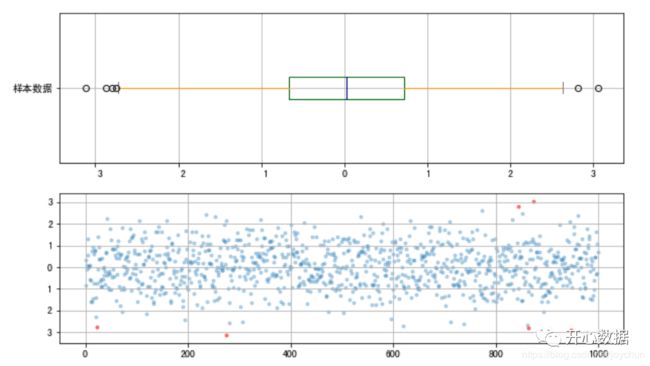
箱型图是非常适合做异常值观察的图形,箱型图的五根线分别表示最大值。最小值、上四分位、下四分位和中位数,箱型图的两个重要的概念是内限和外限,盒须的内限,最大值区间:上四分位+1.5IQR,最小值区间:下四分位-1.5IQR (IQR=上四分位-下四分位),在内限之外是中度异常,在外限之外是极度异常。下面以内限为界,查看异常数据
#箱型图fig = plt.figure(figsize = (10,6))ax1 = fig.add_subplot(2,1,1)color = dict(boxes='DarkGreen', whiskers='DarkOrange', medians='DarkBlue', caps='Gray')data.plot.box(vert=False, grid = True,color = color,ax = ax1,label = '样本数据') s = data.describe()print(s)print('------')# 基本统计量 q1 = s['25%']q3 = s['75%']iqr = q3 - q1mi = q1 - 1.5*iqrma = q3 + 1.5*iqrprint('分位差为:%.3f,下限为:%.3f,上限为:%.3f' % (iqr,mi,ma))print('------')# 计算分位差ax2 = fig.add_subplot(2,1,2)error = data[(data < mi) | (data > ma)]data_c = data[(data >= mi) & (data <= ma)]print('异常值共%i条' % len(error))# 筛选出异常值error、剔除异常值之后的数据data_c plt.scatter(data_c.index,data_c,marker='.',alpha = 0.3)plt.scatter(error.index,error,color = 'r',marker='.',alpha = 0.5)plt.grid()二、缺失值
对于缺失值最简单的处理方法便是删除,但有时不同字段存在大量不同的缺失值,处理起来比较麻烦,如果直接删除将会影响分析结果或者建模的准确率。对于特定的数据一般不直接删除,我把常用的缺失值插补方法分为两类,取名为单一插补法(均值填充、中位数填充、众数填充、特定值填充、临近值填充等)、插值法(拉格朗日插值法、多重插补法等)
1、均值/中位数/众数/特定值/临近值插补
# 创建数据s = pd.Series([1,2,3,np.nan,3,4,5,5,5,5,np.nan,np.nan,6,6,7,12,2,np.nan,3,4]) u = s.mean() # 均值me = s.median() # 中位数mod = s.mode() # 众数print('均值为:%.2f, 中位数为:%.2f' % (u,me))print('众数为:', mod.tolist())print('------')# 分别求出均值/中位数/众数 s.fillna(u,inplace = True)# 用均值填补,可换为中位数、众数或特定的数值等 s1 = pd.Series([1,2,3,np.nan,3,4,5,5,5,5,np.nan,np.nan,6,6,7,12,2,np.nan,3,4]) s1.fillna(method = 'ffill',inplace = True)# 用前值插补 ,后值为bfill2、拉格朗日插值法
拉格朗日插值法的数学原理是,平面上任意点可以拟合成下列多项式
当平面上只有两点时则是最简单的线性关系 ,三点时是二次方,为了根据新的x求出y,需要知道上述公式所有系数,因为n个点在以上多项式上,把n个点的坐标带入,可求出系数,最终求得插值。
from scipy.interpolate import lagrangex = [3, 6, 9]y = [10, 8, 4]print(lagrange(x,y))print(type(lagrange(x,y)))# 输出值为的是多项式的n个系数# 这里输出3个值,分别为a0,a1,a2# y = a0 * x**2 + a1 * x + a2 → y = -0.11111111 * x**2 + 0.33333333 * x + 10 print('插值10为:%.2f' % lagrange(x,y)(10)) # -0.11111111*100 + 0.33333333*10 + 10 = -11.11111111 + 3.33333333 +10 = 2.22222222# 插值10为:2.22下面给出拉格朗日插值法和其他插补方法对比图
data = pd.Series(np.random.rand(100)*100)data[3,6,33,56,45,66,67,80,90] = np.nan data_c = data.fillna(data.median()) # 中位数填充缺失值fig,axes = plt.subplots(1,4,figsize = (20,5))data.plot.box(ax = axes[0],grid = True,title = '数据分布')data.plot(kind = 'kde',style = '--r',ax = axes[1],grid = True,title = '删除缺失值',xlim = [-50,150])data_c.plot(kind = 'kde',style = '--b',ax = axes[2],grid = True,title = '缺失值填充中位数',xlim = [-50,150])# 密度图查看缺失值情况def na_c(s,n,k=5): y = s[list(range(n-k,n+1+k))] # 取数 y = y[y.notnull()] # 剔除空值 return(lagrange(y.index,list(y))(n))# 创建函数,做插值,由于数据量原因,以空值前后5个数据(共10个数据)为例做插值 na_re = []for i in range(len(data)): if data.isnull()[i]: data[i] = na_c(data,i) print(na_c(data,i)) na_re.append(data[i])data.dropna(inplace=True) # 清除插值后仍存在的缺失值data.plot(kind = 'kde',style = '--k',grid = True,title = '拉格朗日插值后',xlim = [-50,150])print('finished!')整体来说,缺失值和异常值的处理虽然技术不难,但要具体情况具体分析,如何进行处理就要靠日常积累的数据分析经验,以上,仅供参考。