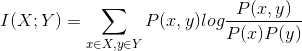信息熵与自然语言处理
本文主要观点来自吴军的《数学之美》
什么是信息熵
信息（Information）是我们天天提到的一个词，信息可以帮助我们减少事物的不确定性。我们要搞清楚一件完全不知道的事物就需要大量的信息，而搞清楚一件熟悉的事情就不需要太多的信息。
从这个角度来说，信息量就等于不确定性的大小，举个例子，假设我错过了世界杯比赛，然后我问看过比赛的人谁是冠军，这个人说让我猜，那几次才能猜中呢。
我们把32支球队从1-32进行编号，首先我猜冠军在1-16号中，如果他说对，我们继续猜冠军在1-8号中...照这样猜下去，一共需要猜5次就可以猜到冠军是谁了。
所以谁是世界杯冠军这条信息的信息量是5，在信息论中使用"比特"（Bit）来描述信息量的大小，也就是这条信息的信息量是5Bit。这是香农（Shannon）提出的信息熵（Information Entropy）概念，用来衡量信息量大小。
具体的，计算信息熵大小公式如下：
其中X是一个随机变量，比如哪只球队获得世界杯冠军。熵的值越大，不确定性就越大，我们需要更多的信息才能消除不确定性。
我们把信息熵套入谁是世界杯冠军这个问题，一共32支球队，假设每个球队获得冠军是等可能的, 
，信息熵为：
也就是当每支球队夺冠可能为等可能的时候，谁是冠军这条信息的信息熵是5比特。但是真实情况下有传统强队和弱队，中国队和德国队夺世界杯的概率肯定是不一样的，也许只猜几次强队就能猜到正确的结果。
对应上面的公式我们只需要调整
的概率就能得到对应的结果。
这就是信息熵，用来描述一个随机事件所含信息量大小。信息熵越高说明这个事件越不确定，信息熵越低说明这个事件就越确定。当随机事件的每个取值等可能发生的时候信息熵最大。
信息熵与自然语言处理
我们该如何在现实世界中使用信息熵呢？
信息熵与文字编码
假设有一本50万汉字的书，我们相对其压缩的话，这本书可以被压缩到多大呢？
我们知道常用的汉字有约7000个，如果每个汉字等可能出现的话，那么表示每个汉字需要13比特（13个二进制数表示）。但是汉字的使用频率是不均衡的，经常使用的汉字只有10%却占据90%的汉字。
如果不考虑上下文，只考虑每个字单独出现的频率，那么每个汉字需要7-8比特。如果再考虑上下文的话，每个汉字的信息熵只有5比特。
那么表示这本书的话只需要250万比特，也就是这本书可以被压缩到一个320KB的文件当中。
再考虑一下霍夫曼树（Huffman Tree）编码文字，也是根据词频大小对字进行二进制编码，这也是跟信息熵有关系。
而Word2Vector的设计也使用了Huffman树，可以看出信息熵跟自然语言处理关系十分的密切。
最大熵模型
最大熵模型可以应用于词性标注、分词等应用，而它的原理就是基于条件熵（Conditional Entropy），定义在
的条件
的熵：
假设一个分类模型的条件概率分布为
，那么
代表样本
属于类别
的概率。
最大熵模型的原理就是在满足约束条件下选择熵最大的那个
互信息
机器翻译中有一个难点是歧义性（Ambiguation），比如bush这个词，既可以表示总统布什也可以表示灌木丛，如何解决这个问题呢？这里可以使用互信息（Mutual Information）：
这是两个事件相关性的度量，就是在了解其中一个事件之后，对事件不确定性所提供的信息量。
上面公式还可以写成
我们只有从语料中计算出
就可以计算出互信息了。
再回到上面这个bush的问题，我们只需要从大量文本中找到跟总统布什互信息最大的词汇，{总统，美国，国会，华盛顿，......}， 再找到跟灌木丛互信息最大的词汇{野生，土壤，植物}，在翻译时当bush这个词出现的时候看上下文出现的哪类相关词多就可以了。
具体计算的话我们可以使用点互信息（point-wise mutual information）计算两个词的相关性
交叉熵
交叉熵（Cross Entropy）是我们在深度学习中经常使用的损失函数：
二分类的时候上述损失函数可以写成
其中
是Label，
是预测值，交叉熵可以计算两个分布的差异，比如对于一个文本二分类问题，有两个样本，他们的标签分别为
是两个模型，假设
是标签为0,反之标签为1，则
这里可以看出交叉熵的一个缺点，明明
模型预测的结果准确率只有50%，但是交叉熵损失的值却更低，Focal Loss可以改进这一缺点，有兴趣的可以自行查看。
另外要说的是，交叉熵实际来自于相对熵（KL Divergence）。
总结
信息熵用来描述事件的不确定性，熵越高，不确定性越大。信息熵的理论与自然语言处理密不可分，很多算法都是基于这一理论。
参考
吴军《数学之美》
https://spaces.ac.cn/archives/4293