机器学习(三十七)——Integrating Learning and Planning(3)
Integrating Learning and Planning
Monte-Carlo Search(续)
下面我们结合实例(下围棋)和示意图,来实际了解MCTS的运作过程。
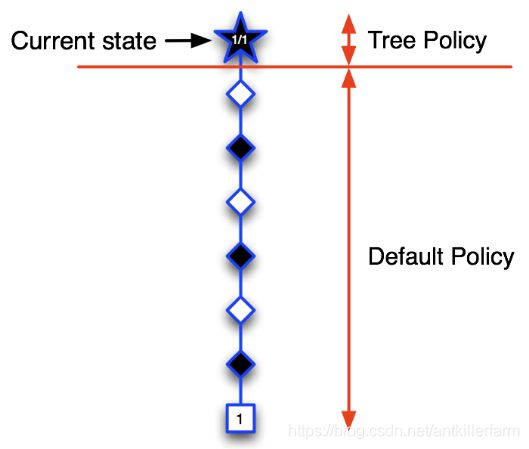
第一次迭代:五角形表示的状态是个体第一次访问的状态,也是第一次被录入搜索树的状态。我们构建搜索树:将当前状态录入搜索树中。使用基于蒙特卡罗树搜索的策略(两个阶段),由于当前搜索树中只有当前状态,全程使用的应该是一个搜索第二阶段的默认随机策略,基于该策略产生一个直到终止状态的完整Episode。图中那些菱形表示中间状态和方格表示的终止状态,在此次迭代过程中并不录入搜索树。终止状态方框内的数字1表示(黑方)在博弈中取得了胜利。此时我们就可以更新搜索树种五角形的状态价值,以分数1/1表示从当前五角形状态开始模拟了一个Episode,其中获胜了1个Episode。
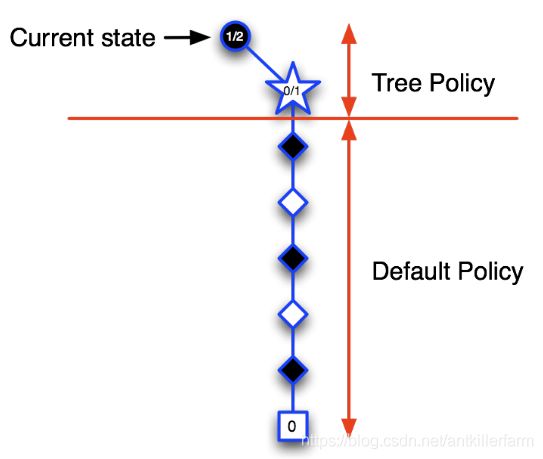
第二次迭代:当前状态仍然是树内的圆形图标指示的状态,从该状态开始决定下一步动作。根据目前已经访问过的状态构建搜索树,依据模拟策略产生一个行为模拟进入白色五角形表示的状态,并将该状态录入搜索树,随后继续该次模拟的对弈直到Episode结束,结果显示黑方失败,因此我们可以更新新加入搜索树的五角形节点的价值为0/1,而搜索树种的圆形节点代表的当前状态其价值估计为1/2,表示进行了2次模拟对弈,赢得了1次,输了1次。
经过前两次的迭代,当位于当前状态(黑色圆形节点)时,当前策略会认为选择某行为进入上图中白色五角形节点状态对黑方不利,策略将得到更新:当前状态时会个体会尝试选择其它行为。
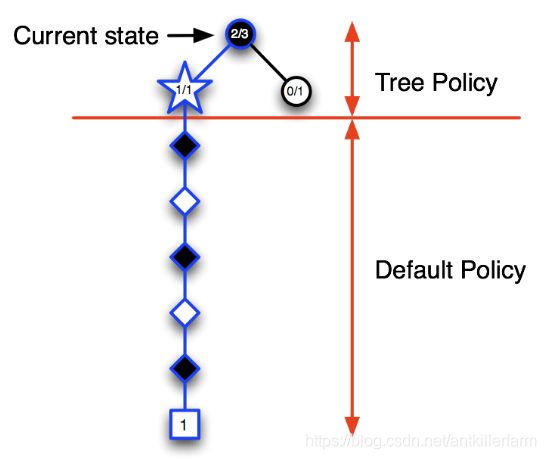
第三次迭代:假设选择了一个行为进入白色五角形节点状态,将该节点录入搜索树,模拟一次完整的Episode,结果显示黑方获胜,此时更新新录入节点的状态价值为1/1,同时更新其上级节点的状态价值,这里需要更新当前状态的节点价值为2/3,表明在当前状态下已经模拟了3次对弈,黑方获胜2次。
随着迭代次数的增加,在搜索树里录入的节点开始增多,树内每一个节点代表的状态其价值数据也越来越丰富。在搜索树内依据 ϵ \epsilon ϵ-greedy策略会使得当个体出于当前状态(圆形节点)时更容易做出到达图中五角形节点代表的状态的行为。
第四次迭代:当个体位于当前(圆形节点)状态时,树内策略使其更容易进入左侧的蓝色圆形节点代表的状态,此时录入一个新的节点(五角形节点),模拟完Episode提示黑方失败,更新该节点以及其父节点的状态价值。
第五次迭代:更新后的策略使得个体在当前状态时仍然有较大几率进入其左侧圆形节点表示的状态,在该节点,个体避免了进入刚才失败的那次节点,录入了一个新节点,基于模拟策略完成一个完整Episode,黑方获得了胜利,同样的更新搜索树内相关节点代表的状态价值。
如此反复,随着迭代次数的增加,当个体处于当前状态时,其搜索树将越来越深,那些能够引导个体获胜的搜索树内的节点将会被充分的探索,其节点代表的状态价值也越来越有说服力;同时个体也忽略了那些结果不好的一些节点(上图中当前状态右下方价值估计为0/1的节点)。需要注意的是,仍然要对这部分节点进行一定程度的探索,以确保这些节点不会被完全忽视。
MCTS的优点:
-
蒙特卡罗树搜索是具有高度选择性的(Highly selective)、导致越好结果的行为越被优先选择(best-first)的一种搜索方法。
-
它可以动态的评估各状态的价值,这种动态更新价值的方法与动态规划不同,后者聚焦于整个状态空间,而蒙特卡罗树搜索是立足于当前状态,动态更新与该状态相关的状态价值。
-
使用采样避免了维度灾难;同样由于它仅依靠采样,因此适用于那些“黑盒”模型(black-box models)。
-
MCTS是可以高效计算的、不受时间限制以及可以并行处理的。
参考:
https://mp.weixin.qq.com/s/4qeHfU9GS4aDWOHsu4Dw2g
记忆增强蒙特卡洛树搜索细节解读
https://zhuanlan.zhihu.com/p/30458774
如何学习蒙特卡罗树搜索(MCTS)
https://zhuanlan.zhihu.com/p/26335999
蒙特卡洛树搜索MCTS入门
https://zhuanlan.zhihu.com/p/25345778
蒙特卡洛树搜索(MCTS)基础
Game Tree
上面围棋示例中的搜索树,在博弈论中,也叫做博弈树(Game Tree)。
Minimax
极小化极大算法(Minimax)是零和游戏常见的策略。通俗的说法就是:选择对自己最有利,而对对手最不利的动作。
Alpha Beta pruning algorithm
在博弈过程中,我们不仅要思考自己的最优走法,还要思考对手的最优走法。而且这个过程是可以递归下去的,直到终局为止。
这样就会形成一整套如下所示的策略序列(以围棋为例,黑棋先下):
黑最优->白最优->黑最优->白最优->…
然后轮到白棋下子:
黑最优->白最优->黑最优->白最优->...
这里的红色字体表示的是已经发生的事件。
可以看的出来,在零和游戏中,我们只需要考虑一方的Game Tree就行了,另一方的Game Tree只是一个镜像而已。这样的话,搜索空间直接就只有原来的一半了。
能不能进一步裁剪呢?这里介绍一下Alpha Beta pruning algorithm。
详细的步骤参见:
http://web.cs.ucla.edu/~rosen/161/notes/alphabeta.html
Minimax with Alpha Beta Pruning
这里只提一下要点:
-
α \alpha α是指the maximum lower bound of possible solutions; β \beta β是指the minimum upper bound of possible solutions。
-
我方下棋会寻找使我方获得最大值的策略,因此叫做MAX结点;敌方下棋显然会寻找能使我方收益最小的策略,因此叫做MIN结点。从Game Tree的角度来看,就是:一层MAX结点->一层MIN结点->一层MAX结点->一层MIN结点->…
-
初始状态:根节点: α = − ∞ , β = ∞ \alpha=-\infty,\beta=\infty α=−∞,β=∞,叶子结点:包含value值。
-
深度优先遍历Game Tree,利用MAX结点的值,更新父结点的 β \beta β值,利用MIN结点的值,更新父结点的 α \alpha α值。
-
一旦出现 α > β \alpha > \beta α>β的情况,则说明遇到了异常分支,直接剪去该分支即可。
参考
https://zhuanlan.zhihu.com/p/55750669
博弈树与α-β剪枝
https://segmentfault.com/a/1190000013527949
Minimax和Alpha-beta剪枝算法简介,以及以此实现的井字棋游戏(Tic-tac-toe)
https://materiaalit.github.io/intro-to-ai-17/part2/
Games
MCTS和MC的区别
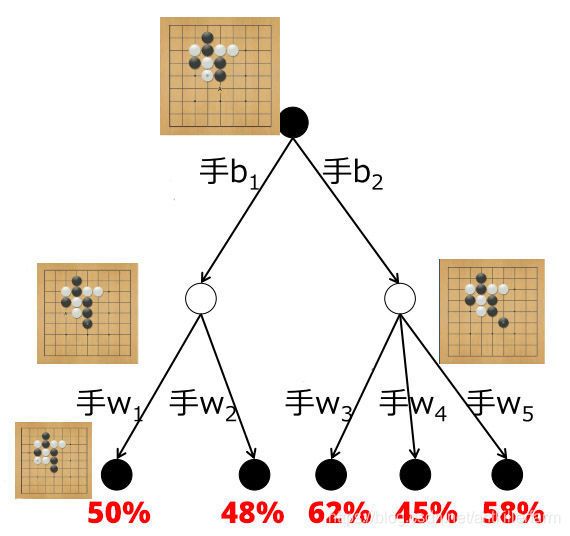
上图是一局围棋的Game Tree的局部。最下面的叶子结点给出了黑棋赢棋的百分比。现在的问题是,黑棋该如何走呢?(假设根节点为当前状态)
如果是用蒙特卡洛方法,趋近的会是其下所有胜率的平均值。例如经过蒙特卡洛模拟,会发现b1后续的胜率是49% = (50+48)/2,而b2后续的胜率是55% = (62+45+58)/3。
于是蒙特卡洛方法说应该走b2,因为55%比49%的胜率高。但这是错误的。因为如果白棋够聪明,会在黑棋走b1的时候回应以w2(尽量降低黑棋的胜率),在黑棋走b2的时候回应以w4(尽量降低黑棋的胜率)。
如果用蒙特卡洛方法做上一百万次模拟,b1和b2的胜率仍然会固定在49%和55%,不会进步,永远错误。所以它的结果存在偏差(Bias),当然,也有方差(Variance)。
而蒙特卡洛树搜索在一段时间模拟后,b1和b2的胜率就会向48%和45%收敛,从而给出正确的答案。所以它的结果不存在偏差(Bias),只存在方差(Variance)。但是,对于复杂的局面,它仍然有可能长期陷入陷阱,直到很久之后才开始收敛到正确答案。
Dyna-2
如果我们把基于模拟的前向搜索应用到Dyna算法中来,就变成了Dyna-2算法。
使用该算法的个体维护了两套特征权重:
-
一套反映了个体的长期记忆,该记忆是从真实经历中使用TD学习得到,它反映了个体对于某一特定强化学习问题的普遍性的知识、经验;
-
另一套反映了个体的短期记忆,该记忆从基于模拟经历中使用TD搜索得到,它反映了个体对于某一特定强化学习在特定条件(比如某一Episode、某一状态下)下的特定的、局部适用的知识、经验。