人工智能学习笔记 - 预备篇之中学统计学概论

这段时间复习初中和高中的数学时惊喜的看到其中有不少关于统计学的一些介绍，我已经不记得当年学习的时候是否有相关的内容了，不过这些基础的概念还是蛮不错的，所以也做了这个笔记记录下来。

统计

统计思想的基础知识能够帮助把随机性归纳于可能的规律性中。统计思想从我们如何观察事物本身如何真正发生两方面，帮助我们理解随机性和规律性的重要性。因此，统计可以看作是一项对随机性中的规律性的研究。同时也是对数据中的偏差问题的研究。

---

统计学基本概念（初中数学）

样本容量：样本中个体的数目
频数：落在不同小组的数据个数为该组的频数
频率：频数与数据总数的比为频率
组数和组距：按照一定的范围分成若干分组，分成组的个数为组数。每一组的两个端点的差叫做组距

平均数：所有样本的和除以样本容量，缺点：易受极值的影响 （也就是我们经常抱怨的“被平均”） x1+x2+x3...+xnn
加权平均数：每个样本乘以不同的权重后的和除以权重之和 x1w1+x2w2+x3w3...+xnwnw1+w2+w3...+wn (注意分母为权重之和而不是样本容量)
中位数：采用大小排列后的样本中最中间的数字为中位数，若个数为奇则取中间一个的值，若个数为偶则取中间两个值的平均值（由于平均数优势不能反映集中趋势）
众数：一组数据中出现次数最多的数据称为这组数据的众数(mode)

方差：各个数据与它们的平均数的差的平方的平均值。主要用来衡量数据的波动和离散性 s2=1n[(x1−x¯)2+(x2−x¯)2+...+(xn−x¯)2]
极差：一组数据中最大和最小值的差（受极值影响大）
平均差：每个数据与它们的平均值的差的绝对值的平均数 |x1−x¯|+|x2−x¯|+...+|xn−x¯|n
标准差：标准差是方差的算术平方根 s=(x1−x¯)2+(x2−x¯)2+...+(xn−x¯)2n−−−−−−−−−−−−−−−−−−−−√

概率 (Probability)：一般把随机事件A发生的概率记作 P(A)
概率的基本计算方法：
- 列举法：将所有的可能结果都列出然后计算概率
- 用频率估计概率：通过大量的重复实验估计概率（比如丢硬币）

---

统计学 （高中数学）

概率
事件=确定事件+随机事件
确定事件=必然事件+不可能事件
若事件A与事件B互斥，则 P(A∪B)=P(A)+P(B)
求概率的方法：
- 试验法：n次试验中事件A出现的频数，称为事件A的频率，当n足够大时，频率接近其概率
- 计算法 （古典/几何）
- 古典概率模型(classical models of probability)：所有出现的基本事件是有限的，每个级别事件出现的可能性是相同的
- 几何概率模型(geometric model of probability)：发生每个事件的概率只与构成该事件区域的长度（面积或体积）成比例

几种采样的方法
- 简单随机采样：在总体N中逐个不放回的抽取n个个体作为样本（ n≤N )，每次抽取时个体的机会相等 （包含“抽签法”和“随机数法”）
- 系统抽样：按照一定的间隔进行抽取
- 分层抽样：按照不同的组/层进行抽样 （e.g 高中组，初中组，小学组）

用样本的频率分布估计总体的分布
分组->制作频率分布表-> 制作直方图-> 连接顶点组成频率分布折线图-> 组距减小折线接近曲线-> 总体密度曲线

当样本数量比较少的情况下，可以采用茎叶图，比如

用样本的数字特征（平均值，标准差等）来估计总体的数字特征

线性回归分析
网络上有大量的关于线性回归分析的资料，主要思想就是画散点图，画回归直线，求回归方程
最小二乘法：样本数据点到回归直线的距离的平方和最小的方法
y=bx+a
考虑有随机误差，标准的线性回归模型为 y=bx+a+e (e为随机误差，e在每个点上的差称为“残差”)

变量间的相关关系
相关性的强弱公式

r=∑ni=1(xi−x¯)(yi−y¯)∑ni=1(xi−x¯)2∑ni=1(yi−y¯)2−−−−−−−−−−−−−−−−−−−−−−−√

若 r 为正数则为正相关，反之为负相关
若 r 落在[-1,-0.75] 表示负相关很强
若 r 落在[0.75,1] 表示正相关很强
若 r 落在[-0.75, -0.3] [0.3,0.75] 表示相关性一般
若 r 落在[-0.25,0.25] 表示相关性很弱

分类变量的相关性
若变量的不同值表示个体属于不同的类别，则该变量称为“分类变量”
通常用来表示两个分类变量的关系的方法是“列联表”，比如

如果没有关系的话则 aa+b≈cc+d 从而 a(c+d)≈c(a+b) 则 ad−bc≈0
ad-bc越小表示关系越弱。统一判断标准采用以下公式：

k2=(a+b+c+d)(ad−bc)2(a+b)(c+d)(a+c)(b+d)

独立性检验原理：在假设H下，如果出现一个与H相矛盾的小概率事件，就判断H不成立，且该推断犯错的概率不超过这个小概率。
反证法原理：在假设H下，如果推出一个矛盾，就证明了H不成立。

离散型随机变量和分布列
所有的取值都可以一一列出的随机变量，叫做离散型随机变量，可用分布列表示

X	x1	x2	…	xi	…	xn
P	p1	p2	…	pi	…	pn

若取 E(X)=x1p1+x2p2+...+xnpn ，称为随机变量x的均值(mean)或数学期望(mathematical expectation)
随机变量X的方差： D(X)=∑ni=1(xi−E(X))2pi

二项分布
在n次独立重复实验中，用X来表示事件A发生的次数，设每次实验事件A发生的概率为p，则满足以下分布的为二项分布：

P(X=k)=Cknpk(1−p)n−k,k=0,1,2,...,n.

正态分布
正态分布曲线

φμ.σ(x)=12π−−√σe−(x−μ)22σ2,x∈(−∞,+∞)

3σ 原则。

优选法
利用数学原理合理安排实验，以最少的实验次数迅速找到最佳点的科学实验方法
单峰函数：比如炮弹发射角度达到最远距离问题
黄金分割法：0.618：比如在一个区间内每次取中间一点则可以按照黄金分割点来取
分数法：当测试变量不连续时，无法采用黄金分割法，用分数近似达到黄金分割的效果，分数采用斐波那契数列 12,23,35,58,813,...
对分法：每次取中间值。比如电线断了，每次从中间开始定位。
黄金分割法是每次把两个试点的结果比较，而对分法是一个试点的结果和已知结果比较
分批实验法：同时进行
多峰的情景：先做均匀实验确认是否多峰
多因素情景：从横对折法和从好点出发法，平行线法，双因素盲人爬山法

正交实验与正交表

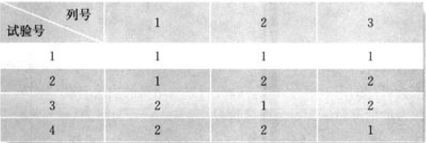
正交表一般用 L4(23) 来表示，4表示有4行即4次实验，3表示有3列即有3中因素，2表示结果值有2个，因此称为2水平正交表
对正交表的实验结果的分析一般采用“直观分析法”，对实验的结果进行求K和R，从而得到最优组合以及确定哪个因素对结果的影响最大。比如：

k1q=12(17+13)=15
k2q=12(19+10)=14.5
依次类推得到其他的K值，同时得到R值 (R值即同一因素的k值的差)， Ra=15−14.5=0.5,Rb=18−11.5=6.5,Rc=16−13.5=2.5 从而推断最优组合是 A1+B1+C2 ，其中B因素影响最大

风险与决策
计算平均损失或收益来进行决策的方法叫风险型决策

上表表示了不同方案下在不同市场情况下收入的损益情况，下表表示了不同市场情况的分布列（概率），因此可以计算平均收益或损失：
Q(d1)=12∗0.3+5∗0.5+(−4)∗0.2=5.3
Q(d2)=8∗0.3+6∗0.5+(−1)∗0.2=5.2
Q(d3)=3∗0.3+3∗0.5+2∗0.2=2.8
观察上述计算，其可转换为矩阵的计算，因此通常称之为损益矩阵
若采用树状结构来表示所有的结果和平均损益，则叫做决策树方法 (若概率的变化对最优决策的影响很大则成为敏感型)

马尔可夫型决策
马尔可夫性：在已知现在的情况下，将来的随机变化规律与过去发生的事件无关
我们称具有马尔可夫性的随机变量序列为马尔可夫链
状态从i到状态j的转移概率
可以将转移概率表示成矩阵，即马尔可夫链的转移概率矩阵
利用马尔可夫链的性质来计算各行动方案的平均收益或风险，以选择最优决策的方法称为马尔可夫决策法

---

对初高中的复习笔记整理告一段落，经历了“相逢好比初相识”，“温故而知新”，“学而时习之，不亦悦乎”的心路历程，也算是给以后辅导儿子做做准备吧：）
接下来开始对人工智能的基本概念进行整理。