cpp简单实现一下BP神经网络
激活函数
σ ( x ) = 1 1 + e − x \sigma (x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
大家都懂,非线性函数
正向传播
X i = σ ( M i ∗ X i − 1 + B i ) {\large X}_{i}=\sigma({\large M}_{i}* {\large X}_{i-1}+{\large B}_{i}) Xi=σ(Mi∗Xi−1+Bi)
简单说明一下
- X 0 X_0 X0 表示输入向量
- X i X_i Xi 表示第i层神经网络的输出向量
- M i M_i Mi表示第i层与第i-1层之间的权重矩阵
- B i B_i Bi表示第i层的偏置向量.
对这个公式进行迭代 就可以实现神经网络的正向传播啦
反向传播
就是链式法制 求一下误差对各个参数的梯度,使用梯度下降法来逼近目标
误差函数 ε = ∑ ( X i − D i ) 2 \text{误差函数}\qquad\varepsilon=\sum_{}{ {\left(X_{i}-D_{i}\right) }^2} 误差函数ε=∑(Xi−Di)2
权重矩阵的偏导 ∂ ε ∂ M i = ∂ ε ∂ X n ∂ X n ∂ X n − 1 ∂ X n − 1 ∂ X n − 2 ⋯ ∂ X i ∂ M i \text{权重矩阵的偏导}\;\frac{\partial \varepsilon}{\partial M_i}= \frac{\partial \varepsilon}{\partial X_{n}} \frac{\partial X_n}{\partial X_{n-1}}\frac{\partial X_{n-1}}{\partial X_{n-2}}\cdots \frac{\partial X_{i}}{\partial M_{i}} 权重矩阵的偏导∂Mi∂ε=∂Xn∂ε∂Xn−1∂Xn∂Xn−2∂Xn−1⋯∂Mi∂Xi
偏置的偏导 ∂ ε ∂ B i = ∂ ε ∂ X n ∂ X n ∂ X n − 1 ∂ X n − 1 ∂ X n − 2 ⋯ ∂ X i ∂ B i \text{偏置的偏导}\;\frac{\partial \varepsilon}{\partial B_i}= \frac{\partial \varepsilon}{\partial X_{n}} \frac{\partial X_n}{\partial X_{n-1}}\frac{\partial X_{n-1}}{\partial X_{n-2}}\cdots \frac{\partial X_{i}}{\partial B_{i}} 偏置的偏导∂Bi∂ε=∂Xn∂ε∂Xn−1∂Xn∂Xn−2∂Xn−1⋯∂Bi∂Xi
为了方便编码,把求偏导的过程稍微整理一下(具体变换过程就不写啦)
D i = ( M i T D i + 1 ) . ∗ X i . ∗ ( 1 − X i ) D_i=(M_i^TD_{i+1}).*X_i.*(1-X_i) Di=(MiTDi+1).∗Xi.∗(1−Xi)
∂ ε ∂ M i = D i . ∗ X i ∂ ε ∂ B i = D i \frac{\partial \varepsilon}{\partial M_i}= D_i.*X_i\qquad\frac{\partial \varepsilon}{\partial B_i}= D_i ∂Mi∂ε=Di.∗Xi∂Bi∂ε=Di
再简单说明一下
- D i D_i Di就是来累加之前的偏导数的, D i D_i Di可以递推算,不过就是要倒着算啦
- 式子中的符号 . ∗ .* .∗ 表示点乘是表示对应位置相乘
- D n D_n Dn中需要赋初值 2 ( X − D ) 2(X-D) 2(X−D)
这样反向传播学习就搞定啦,边算边更新参数就可以啦
简单说下一下代码
创建了一个Matirx矩阵的结构体 struct Matirx
然后又写一个矩阵乘法 void multi(Matirx x,Matirx y,Matirx des)
稍微写一下矩阵的运算 很简单
然后就是BP神经网络的结构体struct NerualCell
一共四个方法:分别是addLayout,bulid,run,train
addLayout:就是向网络中加一下层数,指明每层多少个节点
bulid:就是加完层数后 构建一下整个神经网络’
run:就是执行嘛 正向传播
train:就是学习 反向传播
#include训练的异或结果测试

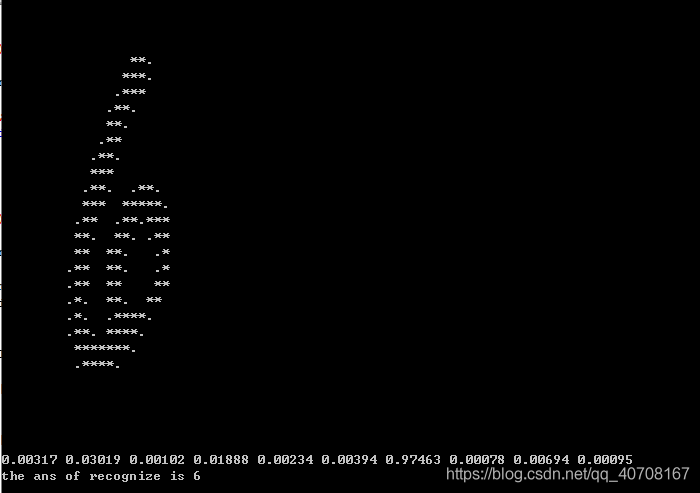
搞一下minst的库,再稍微改改BP神经网络的层数就可以跑一下手写数字的识别啦
void printImageByChar(unsigned char* s,int w,int h){
for(int i=0;i<h;i++)
{
for(int j=0;j<w;j++)
printf("%c",s[i*w+j]>200?'*':s[i*w+j]>100?'.':' ');
printf("\n");
}
}
int main()
{
BP.addLayout(784);
BP.addLayout(196);
BP.addLayout(49);
BP.addLayout(10);
BP.bulid();
FILE *File=fopen("train-images.idx3-ubyte","rb");
unsigned char* TrainImage=new unsigned char[47040020];
fread(TrainImage,1,47040020,File);
fclose(File);
File=fopen("train-labels.idx1-ubyte","rb");
unsigned char* LableImage=new unsigned char[60010];
fread(LableImage,1,60010,File);
fclose(File);
float ans[]={
0,0,0,0,0,0,0,0,0,0};
float input[784];
for(int i=0;i<10000;i++){
memset(ans,0,sizeof(ans));
ans[LableImage[8+i]]=1;
for(int j=0;j<784;j++)input[j]=TrainImage[16+i*784+j]/255.0;
for(int j=0;j<10;j++)
BP.train(input,ans);
printf("\rPlan is training %d/%d",i,10000);
}
printf("\n");
int x;
while(~scanf("%d",&x)){
memset(ans,0,sizeof(ans));
ans[LableImage[8+x]]=1;
for(int j=0;j<784;j++)input[j]=TrainImage[16+x*784+j]/255.0;
Matirx p=BP.run(input);
printImageByChar(TrainImage+16+x*784,28,28);
for(int i=0;i<10;i++)printf("%.5f%c",p.val[i][0],i==9?'\n':' ');
int maxv=0,cmaxv=1;
for(int i=1;i<10;i++){
if(p.val[i][0]>p.val[cmaxv][0])cmaxv=i;
if(p.val[cmaxv][0]>p.val[maxv][0])std::swap(cmaxv,maxv);
}
if(p.val[maxv][0]-p.val[cmaxv][0]<0.1)printf("can't recognize\n");
else printf("the ans of recognize is %d\n",maxv);
}
return 0;
}