机器学习笔记（二）—— 回归的"二三事"

什么是回归？回归的目的是在一堆看似杂乱无章的数字中发现其内在的数学逻辑规律！回归的目的什么？预测，预测明年的房价有多高，预测明年的物价有多高，预测明年的工资水平有多高！当然，在这个大数据时代，靠人脑去对数据集建立回归模型，简直是痴人说梦； 但是在智脑+算法的帮助下，这并不是天方夜谭！现在我们由易至难一一来分析各种常见的回归模型！

一、简单线性回归模型

说到回归，大家脑海中第一反应一定是线性回归了（如果你告诉我是多项式回归，我也不会承认的，我不听……）！现在让我们先从最简单的线性模型说起吧~
我一般把一元一次方程 $y=a\ast x+b$作为简单线性模型，如图1所示！

如何去解决它？很简单，如果我们能够得到a 、b 的值，那么就可以对任意的X进行预测得到y了。对于这种简单的回归模型，我们可以直接通过最小二乘法来得到a、b的值。

（一）如何评价回归模型的优劣

回到最开始的问题，回归的目的是什么？预测，我们要通过回归模型预测出一个Y值 ； 在一个训练集中，每一组数据中我们是存在一个真实的Y值的，因此评价一个回归模型是否可靠，我们可以通过比较预测的Y值与真实的Y值之间的差值的平方来实现，即 均方误差：
$$MSE=\frac{1}{m}\sum _{i=1}^m(f(x^{(i)})-y^{(i)}{)}^2$$
注：m 是数据集的数量 ； f(x) 是线性回归模型 ； y 是真实的值；
很明显可以发现，均方误差越大，则回归模型越差； 均方误差越小， 则回归模型越好！

代码：

'''均方误差（Mwan Squared Error): 用于评价回归算法的准确性'''
def Mean_Squared_Error(y_test,y_predict):
	return np.sum((y_predict-y_test)**2)/len(y_test);

（二）如何优雅地解出模型系数

现在我们有了利器均方误差可以方便我们来评价回归模型的优劣，我们也明白，如果均方误差越小，那么回归模型越好！那么很简单，假设我们建立了一个简单线性回归模型 $y=a\ast x+b$, 那么得到一个a, b值使得均方误差值最小，就可以得到我们想要的回归模型了！

1. 最小二乘法

如何计算
$$min\sum _{i=1}^m(a\ast x^{(i)}+b-y^{(i)}{)}^2$$
就是摆在我们面前的一道难题！数学的问题交给数学，首先，你是否发现这个式子和欧式距离的定义$|X-Y{|}^2$很像，那么如果存在一条直线，使得所有数据点至直线的距离之和最短，这不就是我们的均方误差的定义嘛~好的，问题解决了，这种思路就是 “最小二乘法”！
令$E(a,b)={\sum }_{i=1}^m(a\ast x^{(i)}+b-y^{(i)}{)}^2$, 使其分别对a & b 求偏导： $\frac{\partial E}{\partial a}=0$, $\frac{\partial E}{\partial b}=0$
得：
$$a=\frac{{\sum }_{i=1}^m(x^{(i)}-X_{mean})(y^{(i)}-Y_{mean})}{(x^{(i)}-X_{mean}{)}^2}$$
$$b=Y_{mean}-a\ast X_{mean}$$
所以我们根据上式进行编码就可以很简单地通过计算得想要的简单线性回归模型了！

PS ： 在这里，我想稍微提一下，在上章我们对数据进行KNN分类前，是对数据进行归一化处理过的。那么在回归问题中，数据集是否也需要进行处理呢？假设我们对房价进行预测，你觉得影响房价的各个因素是否是处于相同的数值标准下呢？好吧，如果可以的话，还是进行归一化处理一下吧，毕竟能够很好地提高你的模型准确性。

代码：

import numpy as np
from metrics import r2_score

class SimpleLinearRegression(object):
	'''初始化简单线性回归模型 '''
	def __init__(self):
		self.a_ = None;
		self.b_ = None;
	
	#拟合过程
	def fit(self,x_train,y_train):
		assert x_train.shape == y_train.shape;
		x_mean = np.mean(x_train);
		y_mean = np.mean(y_train);
		self.a_ = (x_train-x_mean).dot(y_train-y_mean)/(x_train-x_mean).dot(x_train - x_mean);      #根据最小二乘法求出相应的系数a,b ； 向量化运算
		self.b_ = y_mean - self.a_*x_mean;
		return self;
	
	#预测过程
	def predict(self,x_test):
		assert x_test.ndim==1;
		y_predict = [self._predict(single) for single in x_test];
		return np.array(y_predict);
	
	#单个样本的回归预测过程
	def _predict(self,x):
		y = self.a_*x+self.b_;
		return y;

2. 梯度下降法

其实在简单线性回归模型中使用梯度下降法，颇有点大炮打蚊子的意味！不过在这里先稍微科普一下什么是梯度下降法，好在下一章直接使用。
什么是梯度下降？这是一种求局部最优解的算法。你可以把下图当作两座山峰，你现在站在山顶上，你要到谷底去，但是你不知道下山的路怎么办？既然你在山上，你要去山底，那么你一定要往下走，所以你走出的每一步只要按照坡度最陡峭的方向向下走，你就是在逐渐靠近山底。

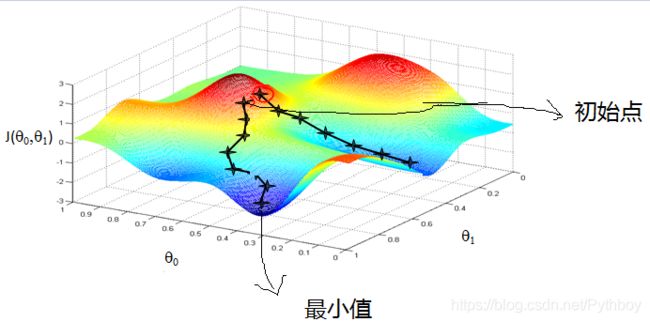
现在我们有一个多元可微函数$F(x)=5X_1+6X_2+7X_3$,则F(x)的梯度为$\nabla F(x)=<\frac{\partial F}{\partial X_1},\frac{\partial F}{\partial X_2},\frac{\partial F}{\partial X_3}>=<5,6,7>$ 。 可以看到，梯度就是分别对每一个变量进行微分处理。

• 在单变量的函数中，梯度就是函数的微分，即在某个点上的切线的斜率
• 在多变量的函数中，梯度是一个有方向的向量，即在某个点上上升的方向

那么回到下山问题，梯度的反方向就是我们在给定点上下降最快的方向，就是我们下山过程中观测到的最陡峭的地方。如果我们沿着梯度的反方向一直往下走，就能够走到局部的最低点。

OK，说了这么多，还是没介绍为什么我们可以在线性回归模型中使用梯度下降法。还记得我们建立回归模型的目标是为了尽可能地减小$E(a,b)={\sum }_{i=1}^m(a\ast x^{(i)}+b-y^{(i)}{)}^2$，现在$x^{(i)},y^{(i)}$ 我们是已知的，该方程是可微的，因此我们完全可以通过梯度下降的思路找到该可微方程的局部极小解（在这里也就是它的全局最小解）！
那么我们该如何使用这种方法呢？请往下看:)

二、线性回归模型

（一） 多样性的评价标准

在上一篇神奇的k中我们提到分类模型的评价标准有准确率、查准率、查全率、F1等，那么在回归模型中，就只有简单的均方误差一种评价标准吗？老实说，分类模型的评价标准确实要远远多于回归模型，但是回归模型的评价标准也确实做到了一招鲜吃遍天（哈哈哈哈），反正你见到的很多回归模型最开始推导的时候都是会采用均方根误差。
不过在这里我想再补充几种分类模型的评价标准，供大家参考！

1. 均方根误差

$$RMSE=\sqrt{MSE}=\sqrt{\frac{1}{m}\sum _{i=1}^m(f(x^{(i)})-y^{(i)}{)}^2}$$
很熟悉的感觉，它就是将之前的均方根误差开个根而已！

2.平均绝对误差

$$MAE=\frac{1}{m}\sum _{i=1}^m|f(x^{(i)})-y^{(i)}|$$

3.R平方

$$R^2=1-\frac{S{S}_{res}}{S{S}_{tot}}=1-\frac{{\sum }_{i=1}^m(f(x^{(i)})-y^{(i)}{)}^2}{{\sum }_{i=1}^m(Y_{mean}-y^{(i)}{)}^2}=1-\frac{MSE(Y_{predict},Y_{True})}{Var(Y_{True})}$$
我们假设这里存在两种回归模型，$f(x)$ 是我们学习建立的回归模型，$Y_{mean}$是我们假设的参考模型（即对于所有输入的X，我们都预测为统一的值$Y_{mean}$，这是一种极不靠谱极不正确的模型），参考模型的均方误差是极大的，因此如果我们建立的回归模型越好，那么$\frac{S{S}_{res}}{S{S}_{tot}}$的值越小，$R^2$也就自然更大。因此通过比较$R^2$的大小，可以定量比较两个回归模型的优劣！个人倾向于通过比较$R^2$来评价线性回归模型。

代码：

'''均方根误差( Root Mean Squared Error) : 用于评价回归算法的准确性'''
def Root_Mean_Squared_Error(y_test,y_predict):
	return sqrt(Mean_Squared_Error(y_test,y_predict));

'''平均绝对误差（Mean Absolute Error): 用于评价回归算法的准确性'''
def Mean_Absolute_Error(y_test,y_predict):
	return np.sum(np.absolute(y_predict-y_test))/len(y_test);

'''R Squared ; 评价回归算法最好的函数'''
def r2_score(y_test,y_predict):
	return 1-Mean_Squared_Error(y_test,y_predict)/np.var(y_test);

(二）求解线性回归模型

1.最小二乘法

现在对于一个多元线性回归模型$Y={\omega }_0+{\omega }_1\ast x_1+{\omega }_2\ast x_2+....+{\omega }_n\ast x_n$, 我们令$X=[1,x]$,$W=[{\omega }_0,{\omega }_1,....,{\omega }_n{]}^T$,则 $Y=XW$
现在我们需要求出合适的$W=[{\omega }_0,{\omega }_1,....,{\omega }_n{]}^T$使得回归模型的损失函数$MSE=\frac{1}{m}{\sum }_{i=1}^m(f(x^{(i)})-y^{(i)}{)}^2$最小，为了方便计算，令$E(W)=\frac{1}{2m}{\sum }_{i=1}^m(f(x^{(i)})-y^{(i)}{)}^2$。好了，现在我们要来求解$E(W)$中的W，使其最小！
$$E(W)=\frac{1}{2m}\sum _{i=1}^m(f(x^{(i)})-y^{(i)}{)}^2=\frac{1}{2m}\sum _{i=1}^m(X^{(i)}W-Y^{(i)}{)}^2=\frac{1}{2m}|XW-Y{|}^2=\frac{1}{2m}(XW-Y{)}^T(XW-Y)$$
$$=\frac{1}{2m}[W^T{X}^{T}XW-W^T{X}^{T}Y-Y^{T}XW+Y^{T}Y]=\frac{1}{2m}[W^T{X}^{T}XW-2W^T{X}^{T}Y+Y^{T}Y]$$
令$$\frac{\partial E(W)}{W}=0$$
则$$\frac{\partial E(W)}{W}=\frac{1}{2m}[W^T{X}^{T}X-2X^{T}Y]=0$$
得：
$$W=(X^{T}X{)}^{-1}{X}^{T}Y$$
好了，上式就是我们根据矩阵方法求得的线性回归系数，但是这种方法具有一定的局限性，首先是对计算量会很大，非常非常的大，如果在大规模数据下你使用该式直接计算回归系数，简直是在作死 ； 其次，上述矩阵推导是在满足可逆条件下进行的，比如说你是10元模型，你只有9条数据，hhhhhh…总之，我们还有神器~

代码：

import numpy as np

class LinearRegression(object):
	def __init__(self):
	'''初始化线性回归模型 '''
		self.coef_ = None;
		self.inter_ = None;
		self._theta = None;
		
	def fit_normal(self,X_train,y_train):
	'''通过正规方程解公式求出线性回归模型中相应的系数向量  '''
		assert len(X_train)==len(y_train);
		X_b = np.hstack([np.ones([len(X_train),1]),X_train]);
		self._theta = ((np.linalg.inv(X_b.T.dot(X_b))).dot(X_b.T)).dot(y_train);
		self.intercept_ = self._theta[0];
		self.coef_ = self._theta[1:];
		return self;
		
	def predict(self,X_test):
	'''线性回归预测结果 '''
		X_b = np.hstack([np.ones([len(X_test),1]),X_test]);
		y_predict = X_b.dot(self._theta);
		return y_predict;

2.梯度下降法

再次提到梯度下降法，没办法，谁让这是解决回归模型的不二神器呢 [摊手]。我们已经了解了什么是梯度下降，接下来我将来介绍在线性回归模型中如何使用梯度下降法！
首先，梯度下降法是用来求解某一函数的局部极小值的，那么我们是要求什么函数的极小值？是线性回归模型本身还是损失函数？当然是损失函数啦，线性回归模型怎么求极小值，会的话教教我 [认真脸]

第一步： 确定损失函数： 在线性回归模型中，损失函数为
$$E(W)=\frac{1}{2}\sum _{i=1}^m(f(x^{(i)})-y^{(i)}{)}^2=\frac{1}{2}(XW-Y{)}^T(XW-Y)$$

第二步：确定损失函数的梯度：
$$\frac{\partial E(W)}{\partial W}=X^T(XW-Y)$$

第三步：迭代求解局部极小值，更新权值W
$$W=W-\alpha \nabla E$$
还记得我们上面提到，梯度的反方向是函数在给定点上下降最快的方向吧，这就是我们为什么要使用负号的原因（PS：如果使用+，那么就是梯度上升法了）
在这里提一下 $\alpha$ 这个值，它是在线性回归模型学习过程中非常重要的超参数，称为 学习率 ；如果学习率过大，会导致迭代过快，从而有可能错过最优解； 如果学习率过小，则迭代次数太慢，很长时间内算法都无法结束。因此选择一个合适的学习率十分重要（ PS：调参虾干的就是这种事了）

核心代码：

def fit_gd(self,X_train,y_train,eta = 0.01,n_iters=1e5):#X-train,y_train是测试集数据， eta 是学习率， n_iters 是最大迭代次数
	'''批量梯度下降法 '''
		def J(theta,X_b,y):    #损失函数
			try:
				return np.sum((X_b.dot(theta)-y)**2)/len(X_b);
			except:
				return float("inf");
			
		def dJ(theta,X_b,y):      #梯度，向量化
			return ((X_b.T).dot(X_b.dot(theta)-y))*2/len(X_b);
			
		def gradientdescent(initial_theta,X_b,y,eta_1 = 0.01,epsilon = 1e-8,n_iters_1 = 1e5): 
		#后面的参数分别是学习率，误差，下降次数
			i_iters = 0;
			theta = initial_theta;
			while i_iters<n_iters_1:       #两个循环条件：一是下降次数；一是误差
				gradient = dJ(theta,X_b,y); #计算梯度
				last_theta = theta; 
				theta = theta - eta_1*gradient; #更新权值
				if abs(J(theta,X_b,y)-J(last_theta,X_b,y))<epsilon:
					break;
			return theta;
		X_b = np.hstack([np.ones([len(X_train),1]),X_train]);        #构建样本向量
		theta = np.zeros([X_b.shape[1],1]);      #初始化θ值
		y_train = y_train.reshape(len(y_train),1);      #改变结果向量的形式
		self._theta = gradientdescent(theta,X_b,y_train,eta_1=eta,n_iters_1=n_iters);   
		self._theta = self._theta.reshape(len(self._theta));    #改变θ向量的形式
		self.intercept_ = self._theta[0];    #求出截距
		self.coef_ = self._theta[1:];    #求出系数
		return self;

3.梯度下降算法的调优

思路一：
选择合适的学习率。上面提过学习率过大或过小都会对算法产生很大的影响。因此需要多次运行后才能得到一个较好的学习率的值。

思路二：
选择合适的W的初始值。由于梯度下降法求得只是局部最小值，因此初始值不同，也许你会得到不同的结果； 当然如果损失函数本身是凸函数的话局部最小解就是最优解！但是我们在很多地方都是可以用到梯度下降算法的，而它却有着局部最优解的风险，因此我们最好还是习惯性地使用不同的初始值来运行算法，减小风险。

思路三：
数据集的归一化处理。前面已经提到，样本不同特征的取值范围是不一定相同的，因此为了减少特征值的影响，对特征数据集进行归一化处理，不仅可以提高算法的准确度，而且还可大大加快迭代次数。磨刀不误砍柴工，何乐而不为呢？

思路四：
随机梯度下降法。Oh，又出现一个新的名词。我们想想，在上面的梯度下降法（又称为批量梯度下降法）中，我们使用了所有样本用于每次迭代过程，因此，加入我有一个很大规模的数据集，那么每次的迭代次数肯定是不会让人很满意的。所以我们需要对批量梯度下降法进行改进，使之在每次迭代过程中，其运算速度能够加快。因此下面我将介绍什么是随机梯度下降法。

4.随机梯度下降法

随机梯度下降法的提出是为了解决批量梯度下降法存在的两个问题：1） 收敛速度可能非常慢 2）如果损失函数存在多个局部极小值，那么不能保证获得全局最优解。
随机梯度的思想很简单，既然全部样本用于训练会过慢，那么每次迭代过程中我只使用一个单独的样本来更新权值，那么迭代次数不就增快许多了。

第一步： 确定损失函数
$$E(W)=\frac{1}{2}\sum _{i=1}^m(f(x^{(i)})-y^{(i)}{)}^2=\frac{1}{2}(XW-Y{)}^T(XW-Y)$$
第二部： 确定梯度并更新权值
1 ) 普通公式
$$W_j=W_j-\alpha (f(X^{(i)})-Y^{(i)})X_j^{(i)}$$
注： 上标 $i$ 表示表示采取第几个样本 ； 下标 $j$ 表示更新第几个权值 或 X样本的第几个特征

2 ) 矩阵形式
$$\frac{\partial E(W)}{\partial W}=X^{(i)T}(X^{(i)}W-Y^{(i)})$$
$$W=W-\alpha X^{(i)T}(X^{(i)}W-Y^{(i)})$$
注： 上标 $i$ 表示表示采取第几个样本

核心代码：

def fit_sgd(self,X_train,y_train,n_iters=5):
	'''随机梯度下降法  '''
		def learning_rate(i_iters):      #学习率
			t0 = 5;
			t1 = 50;
			return t0/(i_iters+t1);
			
		def dJ_sgd(X_b_i,y_i,theta):      
			return ((X_b_i.T).dot(X_b_i.dot(theta)-y_i))*2;

		def sgd(X_b,y,initial_theta,n_iters_1):
			theta = initial_theta;
			i_iters = 0;
			m = len(X_b);
			for i_iters in range(n_iters):
				index = np.random.permutation(m);  #目的是为了能够遍历到所有的样本
				X_b_new = X_b[index]; 
				y_new = y[index];
				for i in range(m):
					eta = learning_rate(i_iters*m+i); #学习率
					X_b_i = X_b_new[i].reshape(1,len(X_b_new[i]));
					y_i = y_new[i].reshape(1,len(y_new[i]));
					gradient = dJ_sgd(X_b_i,y_i,theta); 
					theta = theta - eta*gradient; #更新权值
			return theta;
		X_b = np.hstack([np.ones([len(X_train),1]),X_train]);
		theta = np.zeros([X_b.shape[1],1]);
		y_train = y_train.reshape(len(y_train),1);
		self._theta = sgd(X_b,y_train,theta,n_iters_1=n_iters);
		self._theta = self._theta.reshape(len(self._theta));
		self.intercept_ = self._theta[0];
		self.coef_ = self._theta[1:];
		return self;

三、非线性回归模型

前面主要讲的是线性模型，那是不是在日常使用过程中我们仅仅只会用到线性模型呢？自然不是，像什么指数回归模型、对数回归模型、多项式回归模型等都是经常被使用到的，之所以先向大家介绍线性回归模型的学习方法，只是因为非线性回归模型与线性回归模型的学习过程只隔着一堵墙——数据集的转化！OK，接下来让我们一起一一拆解日常所会接触到的非线性回归模型吧！

1.幂函数模型

一般形式： $y={\beta }_0{x}_1^{{\beta }_1}{x}_2^{{\beta }_2}\dots \dots x_n^{{\beta }_n}$

线性化： $y^{\prime }=lny,{\beta }_0=ln{\beta }_0,x_1^{\prime }=ln{x}_1\dots \dots .,x_n^{\prime }=ln{x}_n$

因此转化为线性回归模型：
$y^{\prime }={\beta }_0^{\prime }+{\beta }_1{x}_1^{\prime }+......+{\beta }_n{x}_n^{\prime }$

2.双曲线模型

一般形式： $\frac{1}{y}={\beta }_0+{\beta }_1\frac{1}{x}$

线性化： $y^{\prime }=\frac{1}{y},x^{\prime }=\frac{1}{x}$

因此转化为线性回归模型：$y^{\prime }={\beta }_0+{\beta }_1{x}^{\prime }$

3. 指数函数模型

一般形式： $y={\beta }_0{e}^{{\beta }_{1}x}$

线性化方法： $y^{\prime }=lny,{\beta }_0^{\prime }=ln{\beta }_0,x^{\prime }=x$

因此转化为线性回归模型: $y^{\prime }={\beta }_0^{\prime }+{\beta }_1{x}^{\prime }$

4. 对数函数模型

一般形式： $y={\beta }_0+{\beta }_{1}lnx$

线性化方法： $y^{\prime }=y,x^{\prime }=lnx$

因此转化为线性回归模型: $y^{\prime }={\beta }_0+{\beta }_1{x}^{\prime }$

5.多项式回归模型

简单的形式: $y={\beta }_0+{\beta }_1{x}^1+{\beta }_2{x}^2+{\beta }_3{x}^3+....+{\beta }_n{x}^n$

线性化方法：$y^{\prime }=y,x_1^{\prime }=x,x_2^{\prime }=x^2,....,x_n^{\prime }=x^n$

因此转化为线性回归模型： $y={\beta }_0+{\beta }_1{x}_1^{\prime }+{\beta }_2{x}_2^{\prime }+....+{\beta }_n{x}_n^{\prime }$

通过比较上述的非线性回归模型的学习过程，一个很重要的特征是： 线性化 ！！！ 所以当我们遇到一个熟悉或不熟悉的非线性回归模型是，重要的是对数据集的线性化处理，将其转化为我们所了然于胸的线性回归模型学习过程，就能够很自然地愉快的解决问题了！

四、欠拟合与过拟合

说了这么多回归模型的学习过程，我们是时候来讨论一下回归模型在学习过程中可能遇到的两种问题： 欠拟合 与 过拟合 ！ 这不仅仅会在回归模型中出现，甚至可以说是整个机器学习过程中都会遇到的困难！

（一） 欠拟合与过拟合

首先我们介绍一下什么是欠拟合和过拟合：
在回归模型学习过程中，我们首先是需要对训练集进行学习，但是如果在训练集的学习过程中，我们的均方误差还是非常大，说明此时的模型并没有充分学习到训练集中的数据。欠拟合通常是由于模型的学习能力低下导致的，这个很容易解决，比如增加随机梯度下降法中的迭代次数、减小学习率等。
但是我们学习一个回归模型，不仅仅是为了得到在训练集中漂亮的数字，我们更期待的是它在一个新的未知的数据集上的表现，也就是期待回归模型的泛化能力强。但是有时候，当学习器把训练样本学的太好了，很可能把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质，这样就会产生过拟合现象。
以下分别是在回归模型以及分类模型中出现的欠拟合、过拟合现象的直观图像：

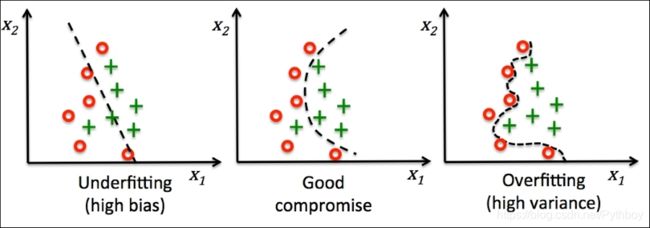
（二）偏差与方差

在上面的第二幅图中，我们出现两个新的概念： 偏差 与 方差！ 这时候你也许会产生疑惑，我们明明在讨论欠拟合与过拟合，为什么还会扯上偏差与方差？它们之间有什么必然的联系吗？
回到我们的回归模型，现在对一个测试样本$X$, 令$y_D$ 为$X$在数据集D上的标记，$y$ 为$X$的真实标记，$f(x;D)$ 为训练集D上学得模型$f$在$X$上的预测输出：
现在令训练集产生的方差为：$$var(x)=E_D[f(x;D)-f_{mean}(x){]}^2$$
噪声为：$${ϵ}^2=E_D[(y_D-y{)}^2]$$
期望输出与真实标记之间的差别称为偏差：$$bia{s}^2(x)=(f_{mean}(x)-y{)}^2$$
那么我们的回归模型的学习算法的期望预测误差为：$$E(f;D)=E_D[f(x;D)-y_D{)}^2]=E_D[f(x;D)-f_{mean}(x){]}^2+(f_{mean}(x)-y{)}^2+E_D[(y_D-y{)}^2]=var(x)+bia{s}^2(x)+{ϵ}^2$$
OK ! 现在你发现点端倪了吧，我们的回归模型的误差本身就可以分解为偏差、方差以及噪声之和！
现在我们来明确义下偏差、方差以及噪声的含义：

1.偏差： 度量学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合程度
2.方差： 度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响
3.噪声： 表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，刻画了学习任务本身的难度

下图十分形象的刻画了偏差与方差的定义：

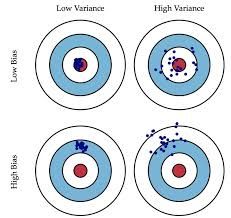
对于一个给定的学习任务，为了取得最好的泛化能力，一方面我们需要使偏差较小，即能够充分的拟合数据 ； 另一方面要使方差较小，即使得数据扰动产生的影响小。
但是很遗憾的是，偏差和方差在大多数情况下是冲突的存在，即存在如下图所示的偏差-方差窘境。假设我们现在可以控制学习算法的训练程度，如果此时我们令其训练不足，那么学习器的拟合能力较差，训练数据的扰动是不足以使学习器发生明显的变化的，此时是偏差主宰了回归误差，这时发生的是欠拟合现象 ； 如果我们此时令学习算法的拟合能力超强，使其都能够学到一些数据集中很弱的特征，那么训练数据发生的微小的扰动都会被学习器学习到，因此方差开始主导了回归误差，这种现象称之为过拟合现象。

总结：欠拟合——偏差，过拟合——方差。

（三）学习曲线

现在我们已经介绍了什么是回归模型的过拟合与欠拟合、以及回归模型的误差与偏差、方差之间的联系。那么我们如何去判断已经学习到的模型是否存在欠拟合与过拟合现象呢？这里，我将介绍一项简单的工具让您可以直观地看出自己模型所处的状态 —— 学习曲线。

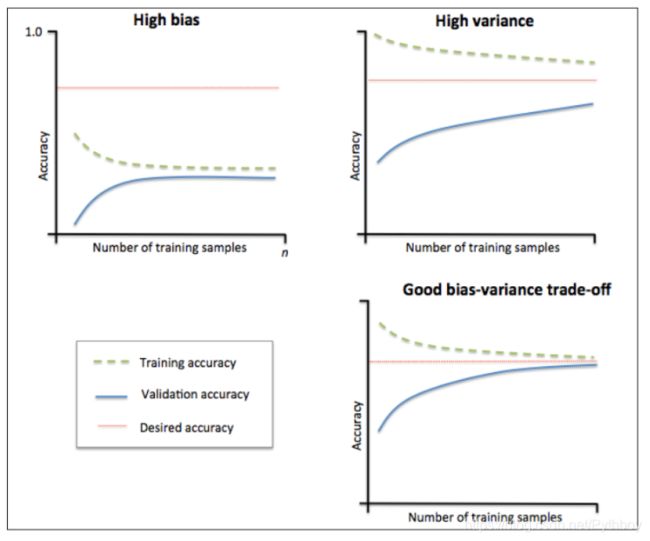
1.左上图：训练集准确率与测试集准确率收敛，但是远小于期望中的准确率，所以属于欠拟合问题（偏差）
2.右上图：训练集准确率高于期望值，测试集准确率低于期望值，二者之间存在较大间距，属于过拟合问题（方差）
3.右下图：训练集与测试集的准确率收敛于期望值，低偏差、低方差，优秀！

下面介绍学习曲线的思路：

'''
1. 首先确定训练集和测试集，然后分别从数据集中选取相同数量的样本
2. while 样本数量（从小到大）：
          使用训练集的样本训练模型，并确定模型的准确率/均方误差；使用学习好的模型用于测试集，确定准确率及均方误差；
          作图;
'''

代码：

#learning curve
def plot_learning_curve(algo,x_train,x_test,y_train,y_test):
	train_score=[];
	test_score = [];
	for i in range(1,len(x_train)+1):
		algo.fit(x_train[:i],y_train[:i]);
		y_train_predict = algo.predict(x_train[:i]);
		y_test_predict = algo.predict(x_test);
		train_score.append(mean_squared_error(y_train[:i],y_train_predict[:i]));
		test_score.append(mean_squared_error(y_test,y_test_predict));
	plt.figure()
	plt.plot([i for i in range(1,len(x_train)+1)],np.sqrt(train_score),label = "train score");
	plt.plot([i for i in range(1,len(x_train)+1)],np.sqrt(test_score),label = "test score");
	plt.legend(loc="best");
	plt.axis([0,len(x_train)+1,0,4]);
	plt.show();

（四）过拟合问题的处理方式

相对于可以简单克服的“欠拟合”问题，过拟合线性才是横亘于机器学习面前的关键障碍！
这个问题太复杂了，不是我所能掌控的，我只能简单的提供一些自己了解的思路，大家八仙过海，各显本事把 [无奈脸] :

• 重新清洗数据 ： 导致过拟合的一个原因有可能是数据不纯导致的，可以通过重新清洗数据加以检验
• 增大数据的训练量： 导致过拟合的一个原因有可能是由于我们用于训练的数据量过小导致的，因此可以尝试增大用于训练的数据量
• 采用dropout方法：这是神经网络中的常用方法，通俗原理是在使用dropout方法训练的时候让神经元在一定的概率下不进行工作。具体原理及操作请自行查询！
• 正则化方法 （包括L0正则，L1正则，L2正则），一般是在母表函数之后加上对应的范数。L0范数是指向量中非0的元素的个数 ； L1范数是指向量中各个元素绝对值之和 ； L2范数是指向量各元素的平方和然后求根，可以起到使权值$W$ 变小加剧的作用，更小的参数$W$意味着复杂度更低的学习模型，有效减弱过拟合现象，复合奥卡姆剃刀的原则。

Pay Attention ： 请各位看客一定要注意，虽然我是以回归模型为切入点来介绍欠拟合&过拟合、偏差&方差，但是这两个问题是贯穿于整个机器学习的所有模型中的，您完全可以直接套用在分类模型、聚类模型等等！！！！！

五、岭回归与LASSO回归

前面说了这么多过拟合与欠拟合的问题，也许你会不耐烦了，干啥呢？干啥呢？回归哪有这么多问题？嘿，你还别不信，在回归中，过拟合现象是十分常见的，因此针对如何处理回归模型中的过拟合现象的发生，也有系统的处理办法。还记得上一部分提到的解决过拟合现象中的一种解决思路是使用正则化方法吗？在回归模型中，针对L1正则化、L2正则化，有两个专门回归模型，分别是岭回归模型与LASSO回归模型。这就是接下来介绍的重点内容，各位看客，好戏登场！

（一）岭回归

回忆一下，在线性回归模型中，我们的目标是优化损失函数使之最小：$$min\frac{1}{m}\sum _{i=1}^m(X^{(i)}W-Y^{(i)}{)}^2$$
岭回归减小过拟合现象发生风险的方法是在上面的损失函数后面加上L2范数，使之形式变化为
$$min\frac{1}{m}\sum _{i=1}^m(X^{(i)}W-Y^{(i)}{)}^2+\lambda ||W|{|}^2(\lambda >0)$$

现在让我们按照线性回归模型推导的过程来推导一下上面的损失函数：

1.1 矩阵计算

$J(\omega )$
$=\frac{1}{2m}{\sum }_{i=1}^m(X^{(i)}W-Y^{(i)}{)}^2+\lambda ||W|{|}_2^2$
$=\frac{1}{2m}(XW-Y{)}^T(XW-Y)+\lambda W^{T}W$
$=\frac{1}{2m}(Y^{T}Y-Y^{T}XW-W^T{X}^{T}Y+W^T{X}^{T}XW)+\lambda W^{T}W$
令 $$\frac{\partial J(W)}{\partial W}=0$$
则：$$0-2X^{T}Y+2X^{T}XW+2\lambda W=0$$
得：
$$W=(X^{T}X+\lambda I{)}^{-1}{X}^{T}Y$$
单位矩阵$I$得对角线上全是1，像一条山岭一样，这就是岭回归名称的由来。同时，由于L2范数的加入，使得$(X^{T}X+\lambda I)$ 满秩，保证了可逆，但是同时也会使得回归系数$W$的估计不再是无偏估计。因此岭回归是以降低精度为代价来解决过拟合问题的一种回归方法。

1.2 梯度下降法

首先让我们愉快的求出损失函数的梯度：
$$\frac{\partial J(W)}{\partial W_j}=\frac{1}{m}\sum _{i=1}^m(X^{(i)}{W}_j-Y^{(i)})X_j^{(i)}+2\lambda W_j$$
迭代公式如下：
$$W_{j+1}=W_j-\frac{\alpha }{m}\sum _{i=1}^m(X^{(i)}{W}_j-Y^{(i)})X_j^{(i)}-2\lambda W_j$$
$$=(1-2\lambda )W_j-\frac{\alpha }{m}\sum _{i=1}^m(X^{(i)}{W}_j-Y^{(i)})X_j^{(i)}$$

是不是很精彩，一下在豁然开朗！具体的代码这里就不展示了，将最开始的线性回归代码稍微改一下就OK了，看好你哟！

1.3 $\lambda$的选择

对于岭回归的$\lambda$而言，随着$\lambda$的增大，$(X^{T}X+\lambda I{)}^{-1}$ 就越小，模型的方差也就越小，但是与此同时， 回归系数$W$的估计值也就愈加偏离真实的学习值，模型的偏差也就逐渐增大。因此岭回归实际上是一个增大偏差减小方差的回归模型，而评判岭回归是否是一个优秀的学习模型的关键在于是否能够找到一个合理的$\lambda$来平衡模型的方差和偏差。

• 岭迹法确定$\lambda$值 ： 由$W=(X^{T}X+\lambda I{)}^{-1}{X}^{T}Y$可知W是$\lambda$的函数，因此在平面坐标系中的$W$ - $\lambda$ 称为岭迹曲线。当$W$趋于稳定的点就是所要寻找的$\lambda$值
• 交叉验证法确定$\lambda$值 ：通过交叉验证的方式，训练和测试对应的一个模型及均方误差，进而得到一个平均评分。选择平均评分最高的$\lambda$值。

（二）LASSO回归

LASSO回归，全称为 Least Absolute Shrinkage and Selection Operator ，注意到Selection这个单词了吗？LASSO回归是通过L1范数来快乐风男（压缩 ? ）模型的系数，使得一些系数变小，甚至使一些绝对值较小的系数直接变为0，是一种用于估计稀疏参数的线性模型，特别适用于参数数目的数目缩减即 特征选择（注：这是岭回归无法做到的，也是二者之间最大的区别）

2.1 LASSO回归解法

首先让我们确定LASOO模型的 损失函数：
$$J(W)=\sum (XW-Y{)}^2+\alpha ||W|{|}_1$$
在这里，我们已经无法再向上面一样轻松了，因为L1范数惩罚项是绝对值形式，所以在零点处不可导，所以我们无法采用梯度下降法了[?]. 解决LASSO回归主要由两种解法： 坐标轴下降法 以及 最小角回归法！具体的推导过程太复杂了，这里就不展开了，有兴趣的看客可以自行推导！结果为：

$W_j=\frac{(m_j-\frac{\alpha }{2})}{n_j}，当m_j>\frac{\alpha }{2}$
$W_j=0,当m_j\in [-\frac{\alpha }{2},\frac{\alpha }{2}]$
$W_j=\frac{(m_j+\frac{\alpha }{2})}{n_j}，当m_j<-\frac{\alpha }{2}$

其中：$m_j={\sum }_{i=1}^n{X}_j^{(i)}(Y^{(i)}-{\sum }_{k̸=j}{W}_k{X}_k^{(i)})$ ; $n_j={\sum }_{i=1}^n{X}_j^{(i)2}$

2.2 超参数$\alpha$的选择

对于LASSO回归的算是函数而言，$\alpha$ 控制了稀疏参数估计的惩罚程度，这里提供两种常用的模型选择工具来实现$\alpha$的选择：

• 交叉验证： 交叉验证真的是万金油，在岭回归中可以使用，在LASSO回归中也能使用。方法是不变的，就看你会不会用了！
• 基于信息准则的模型选择：赤池信息量准则（AIC）：$AIC=2k-2ln(L)$ ;贝叶斯信息准则 （BIC）： $BIC=2kln(k)-2ln(L)$ ; 其中$L$为模型极大似然函数的最大值，而$k$是模型参数的个数； 优先考虑的模型应该是AIC值或BIC值最小的那一个！

难得写这么长的博客，既是对自己的总结，也是希望能够对大家有所帮助！与君共勉！