李英俊小朋友
李英俊小朋友

《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记

《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记

文章目录

  • 《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记
    • 写在前面
    • 1. 机器学习概览
    • 2. 端到端的机器学习项目
    • 3. 分类
    • 4. 训练模型
    • 5. 支持向量机
    • 6. 决策树
    • 7. 集成学习和随机森林
    • 8. 降维
    • 9. 运行TensorFlow
    • 10. 人工神经网络简介
    • 11. 训练深度神经网络
    • 12. 跨设备和服务器的分布式TensorFlow
    • 13. 卷积神经网络
    • 14. 循环神经网络
    • 15. 自动编码器
    • 16. 强化学习

写在前面

  • 本书的书评已更新，不推荐看此书，传送门

1. 机器学习概览

  1. 你会怎么定义机器学习？

    机器学习是一门能够让系统从数据中学习的计算机科学。

  2. 最常见的两个监督式任务是回归和分类。

  3. 常见的无监督式任务包括聚类、可视化、降维和关联规则学习。

  4. 在线学习系统可以进行增量学习，与批量学习系统正好相反。这使得它能够快速适应不断变化的数据和自动化系统，并且能够在大量的数据上进行训练。

  5. 核外算法可以处理计算机主内存无法应对的大量数据。它将数据分割成小批量，然后使用在线学习技术从这些小批量中学习。

  6. 模型参数与学习算法的超参数之间有什么区别？

    模型有一个或多个参数，这些参数决定了模型对新的给定实例会做出怎样的预测（比如，线性模型的斜率）。学习算法试图找到这些参数的最佳值，使得该模型能够很好的泛化至新的实例。超参数是学习算法本身的参数，不是模型的参数（比如，要应用的正则化数量）。

  7. 基于模型的学习算法搜索是什么？它们最常使用的策略是什么？它们如何做出预测？

    基于模型的学习算法搜索使模型泛化最佳的模型参数值。通常通过使成本函数最小化来训练这样的系统，成本函数衡量的是系统对训练数据的预测有多坏，如果模型有正则化，则再加上一个对模型复杂度的惩罚。学习算法最后找到的参数值就是最终得到的预测函数，只需要将实例特征提供给这个预测函数即可进行预测。

  8. 机器学习面临的一些主要挑战是：数据缺乏、数据质量差、数据不具代表性、特征不具信息量、模型过于简单对训练数据拟合不足、以及模型过于复杂对训练数据过拟合。

  9. 如果你的模型在训练数据上表现好，但是应用到新的实例上的泛化结果却很糟糕，是怎么回事？能提出三种可能的解决方案吗？

    该模型很可能过度拟合训练数据（或者在训练数据上运气太好）。

    可能的解决方案是：获取更多数据，简化模型（选择更简单的算法、减少使用的参数或特征数量、对模型正则化），或者是减少训练数据中的噪声。

  10. 验证集的目的是什么？

    验证集用来比较不同模型。它可以用来选择最佳模型和调整超参数。

  11. 如果使用测试集调整超参数会出现什么问题？

    如果使用测试集来调整超参数，会有过度拟合测试集的风险，最后测量的泛化误差会过于乐观（最后启动的模型性能比预期的要差）。

  12. 什么是交叉验证？它为什么比验证集更好？

    通过交叉验证技术，可以不需要单独的验证集实现模型比较（用于模型选择和调整超参数）。者节省了宝贵的训练数据。

2. 端到端的机器学习项目

  • 回归问题的性能指标

    • 均方根误差（RMSE）： 1 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 \sqrt {\frac{1}{m} \sum\limits_{i=1}^m ( h(x^{(i)}) - y^{(i)} ) ^2} m1​i=1∑m​(h(x(i))−y(i))2 ​，对应 l 2 l_2 l2​范数。
    • 平均绝对误差（MAE）： 1 m ∑ i = 1 m ∣ h ( x ( i ) ) − y ( i ) ∣ \frac{1}{m} \sum\limits_{i=1}^m | h( x^{(i)} ) - y^{(i)} | m1​i=1∑m​∣h(x(i))−y(i)∣，对应 l 1 l_1 l1​范数。
    • 范数指数越高，则越关注大的价值，忽略小的价值。这就是为什么RMSE比MAE对异常值更敏感。但是当异常值非常稀少（例如钟形曲线）时，RMSE的表现优异，通常作为首选。

  • df.where详解

    • 参考连接：https://blog.csdn.net/brucewong0516/article/details/80226990
      • 返回一个同样shape的df，当满足条件为TRUE时，从本身返回结果，否则从返回其他df的结果
    • df.mask使用时，结果与where相反

  • 分层抽样详解

    • sklearn.model_selection.StratifiedShuffleSplit
      • 参考链接：https://blog.csdn.net/m0_38061927/article/details/76180541

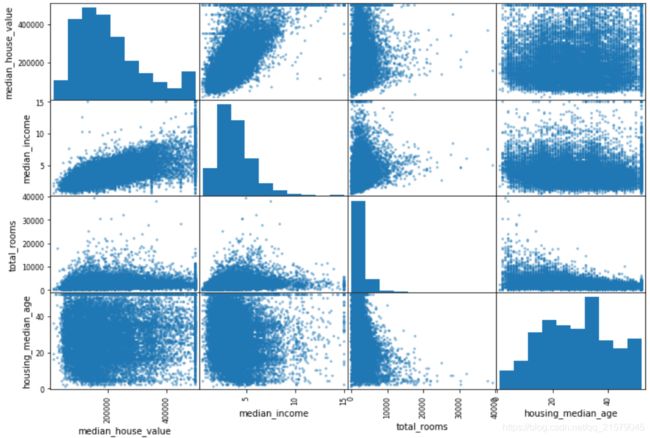
  • 检验属性之间的相关性

    • from pandas.plotting import scatter_matrix《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第1张图片

  • 缺失值处理

    • from sklearn.preprocessing import Imputer
      • 预处理数据的方法总结

  • 处理文本和分类属性

    • from sklearn.preprocessing import LabelEncoder
      • LabelEncoder
      • 这种代表方式产生的一个问题是，机器学习算法会一位两个相近的数字比两个离得较远的数字更为相似一些，然而真实情况并非如此。
    • from sklearn.preprocessing import OneHotEncoder
      • OneHotEncoder
    • from sklearn.preprocessing import LabelBinarizer
      • LabelBinarizer
      • 使用LabelBinarizer类可以一次性完成两个转换
      • 从文本类别转换为整数类别，再从整数类别转换为独热向量
      • 这时默认返回的是一个密集的Numpy数组，通过发送sparse_output=True，可以得到稀疏矩阵

  • 特征缩放

    • 最大最小缩放（归一化）：MinMaxScaler
    • 标准化：StandardScaler

  • 用numpy连接两个矩阵

    • np.c_和np.r_的用法解析
    • np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等。
    • np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等。

  • 交叉验证

    • sklearn的交叉验证功能更倾向于使用效用函数（越大越好），而不是成本函数（越小越好），所以计算分数的函数实际上是负的MSE（一个负值）函数，这就是为什么上面的代码在计算平方根之前会先计算出-scores。

3. 分类

  • MNIST数据报错：[WinError 10060] 由于连接方在一段时间后没有正确答复或连接的主机没有反应，连接尝试失败。

    参考链接：scikit-learn使用fetch_mldata无法下载MNIST数据集问题解决方法

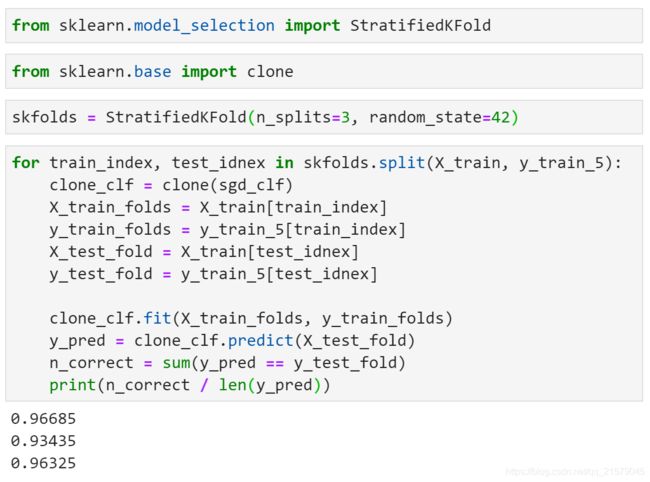
  • StratifiedKFold

    • 相比于cross_val_score()这一类交叉验证函数，该函数可以让你能控制的更多一些，你可以自行实施交叉验证。

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第2张图片

  • cross_val_predict

    • 返回的不是评估分数，而是每个折叠的预测值
    • 得到的是一维数组，你想啊，多折之后每个样本都会且仅会成为一次验证集，所以，得到的是跟原样本数量一致的预测的label

  • confusion_matrix

    • 混淆矩阵
    • 混淆矩阵中的行表示实际类别，列表示预测类别。

  • decision_function()

    • 该方法返回每个实例的分数，然后就可以根据这些分数，使用任意阈值进行预测。

    • 使用cross_val_predict()函数获取训练集中所有实例的分数

      y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")

    • 有了这些分数，可以使用precision_recall_curve()函数来计算所有可能的阈值的精度和召回率

      precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

      def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision")
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall")
    plt.xlabel("threshold")
    plt.legend(loc = "upper left")
    plt.ylim([0, 1])

plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.show()

  • roc_curve()

    • 受试者工作特征曲线

      from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--')
    plt.axis([0, 1, 0, 1])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
plot_roc_curve(fpr, tpr)
plt.show()

  • roc_auc_score()

    • 有一种比较分类器的方法是测量曲线下面积（AUC）
    • 完美的分类器的ROC AUC等于1，而纯随机分类器的ROC AUC等于0.5。
    • from sklearn.metrics import roc_auc_score

  • ROC和PR曲线的选择

    • 由于ROC曲线与精度/召回率（PR曲线）非常相似，因此你可能会问如何决定使用哪种曲线。
    • 有一个经验法则是，当正类非常少见或者你更关注假正类而不是假负类时，你应该选择PR曲线；反之则是ROC曲线。PR曲线越接近右上角越好。

  • 多类别分类器

    • sklearn可以检测到你尝试使用二元分类算法进行多类别分类任务，它会自动运行OvR(SVM分类器除外，它会使用OvO)。

    • 如果想要强制sklearn使用一对一或者一对多策略，可以使用OneVsOneClassifier或OneVsRestClassifier类。

      from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(X_train, y_train)
ovo_clf.predict([some_digit])
len(ovo_clf.estimators_)

  • 错误分析：cross_val_predict() + confusion_matrix()

4. 训练模型

  • 线性回归算法比较

    算法 m很大 是否支持核外 n很大 超参数 是否需要缩放 sklearn
    标准方程 快 否 慢 0 否 LinearRegression
    批量梯度下降 慢 否 快 2 是 n/a
    随机梯度下降 快 是 快 ≥2 是 SGDRegressor
    小批量梯度下降 快 是 快 ≥2 是 n/a

    其中，m是训练实例的数量，n是特征数量。

  • 多项式特征

    • from sklearn.preprocessing import PolynomialFeatures
    • PolynomialFeatures会在给定的多项式阶数下，添加所有的特征组合
    • 例如两个特征a，b，阶数degree=3，PolynomialFeatures不只会添加特征 a 2 a^2 a2、 a 3 a^3 a3、 b 2 b^2 b2、 b 3 b^3 b3，还会添加组合 a b ab ab、 a 2 b a^2b a2b、 a b 2 ab^2 ab2。

  • 偏差/方差权衡

    • 在统计学和机器学习领域，一个重要的理论结果是，模型的泛化误差可以被表示为三个截然不同的误差之和：
      • 偏差：错误的假设（假设数据是线性的）。
      • 方差：对数据的微小变化过度敏感（过拟合）。
      • 不可避免的误差：噪声（通过清理数据来改善噪声）。

  • 线性回归

    • 普通线性回归：from sklearn.linear_model import LinearRegression
    • 岭回归（l2范数正则化）：from sklearn.linear_model import Ridge
    • 套索回归（l1范数正则化）：from sklearn.linear_model import Lasso
    • 弹性网络（岭回归和套索回归的混合）：from sklearn.linear_model import ElasticNet

  • 练习部分摘抄

    • 如果你的训练集里特征的数值大小迥异，什么算法可能会受到影响？受影响程度如何？你应该怎么做？

      如果训练集的特征数值具有非常迥异的尺寸比例，成本函数将呈现为细长的碗状，这导致梯度下降算法将耗费很长时间来收敛。要解决这个问题，需要在训练模型之前先对数据进行缩放。值得注意的是，使用标准方程法，不经过特征缩放也能正常工作。

    • 训练逻辑回归模型时，梯度下降是否会困于局部最小值？

      不会，因为它的成本函数是凸函数。

    • 假设你使用的是批量梯度下降，并且每一轮训练都绘制出其验证误差，如果发现验证误差持续上升，可能发生了什么？你如何解决这个问题？

      可能性之一是学习率太高，算法开始发散所致。如果训练误差也开始上升，那么很明显你要降低学习率了。但是，如果训练误差没有上升，那么模型可能过度拟合训练集，应该立即停止训练。

    • 哪种梯度下降算法能最快达到最优解的附近？那种会收敛？如何使其他算法同样收敛？

      随机梯度下降的训练迭代最快，因为它一次只考虑一个训练实例，所以通常来说，它会最快到达全局最优的附近（或者是批量非常小的小批量梯度下降）。但是，只有批量梯度下降才会经过足够长时间的训练后真正收敛。对于随机梯度下降和小批量梯度下降来说，除非逐渐调低学习率，否则将一直围绕最小值上上下下。

5. 支持向量机

  • 核函数

    • linear、poly、rbf、sigmoid。
    • 有那么多核函数，该如何决定使用哪一个呢？有一个经验法则是：永远先从线性核函数开始尝试。
    • 要记住，LinearSVC比SVC(kernel=“linear”)快得多，特别是训练集非常大或者特征非常多的时候。
    • 如果训练集不大，可以试试高斯RBF核，大多数情况下它都非常好用。

  • 用于SVM分类的sklearn类的比较

    类 时间复杂度 是否支持核外 是否需要缩放 核技巧
    LinearSVC O(mxn) 否 是 否
    SGDClassifier O(mxn) 是 是 否
    SVC O( m 2 m^2 m2xn)-O( m 3 m^3 m3xn) 否 是 是

  • 练习摘抄

    • 使用SVM时，对输入值进行缩放为什么重要？

      支持向量机拟合类别之间可能的/最宽的街道，所以如果训练集不经过缩放，SVM将趋于忽略值较小的特征。

    • SVM分类器在对实例进行分类时，会输出信心分数吗？概率呢？

      支持向量机分类器能够输出测试实例与决策边界之间的距离，你可以将其作为信心分数。但是这个分数不能直接转化为类别概率的估算。如果创建SVM时，在sklearn中设置probability=True，那么训练完后，算法将使用逻辑回归对SVM分数进行校准（对训练数据额外进行5折交叉验证的训练），从而得到概率值。这会给SVM添加predict_proba()核predict_log_proba()两种方法。

    • 如果训练集有上千万个实例核几百个特征，你应该使用SVM原始问题还是对偶问题来训练模型呢？

      这个问题仅适用于线性支持向量机，因为核SVM只能使用对偶问题。对于SVM问题来说，原始形式的计算复杂度与训练实例的数量成正比，而其对偶形式的计算复杂度与某个介于 m 2 m^2 m2和 m 3 m^3 m3之间的数量成正比。所以如果实例的数量以百万计，一定要使用原始问题，因为对偶问题会非常慢。

6. 决策树

  • 决策树的可视化

    • 生成一个决策树模型tree_clf

    • 导出成dot格式的文件

      export_graphviz(
    tree_clf,
    out_file=("./iris_tree.dot"),
    feature_names=iris.feature_names[2:],
    class_names=iris.target_names,
    rounded=True,
    filled=True
)

    • dot转png

      dot -Tpng iris_tree.dot -o iris_tree.png

  • 决策树的优势

    • 需要的数据准备工作非常少。特别是，完全不需要进行特征缩放或集中。
    • sklearn使用的时CART算法，该算法仅生成二叉树。但是其他算法，比如ID3生成的决策树，其节点可以拥有两个以上的子节点。
    • CART时一种贪婪算法：从顶层开始搜索最优分裂，然后每层重复这个过程。贪婪算法通常会产生一个相当不错的解，但是不能保证是最优解。
    • 预测复杂度： O ( l o g 2 ( m ) ) O(log_2(m)) O(log2​(m))，与特征数量无关，所以即使是处理大型数据集，预测也很快。
    • 训练复杂度： O ( n ∗ m l o g ( m ) ) O(n*mlog(m)) O(n∗mlog(m))，对于小型训练集（几千个实例以内），sklearn可以通过数据预处理（设置presort=True）来加快训练，但是对于较大的训练集而言，可能会减慢训练的速度。

  • 基尼不纯度还是信息熵

    • gini不纯度 = 1 - 求和【(类别为k的训练实例的占比)^2】
    • 信息熵 = - 求和【(类别为k的训练实例占比)*log(类别为k的训练实例占比)】
    • 大多数情况下，它们并没有什么大的不同，产生的树都很相似。
    • gini不纯度计算速度略微快一些。
    • 基尼不纯度倾向于从树枝中分裂出最常见的类别。
    • 信息熵倾向于生产更平衡的树。

  • 正则化超参数

    • max_depth：最大深度
    • min_samples_split：分裂前节点必须有的最小样本数
    • min_samples_leaf：叶节点必须有的最小样本数
    • min_weight_fraction_leaf跟min_samples_leaf一样，但表现为加权实例总数的占比
    • max_leaf_nodes：最大叶节点数量
    • max_features：分裂每个节点评估的最大特征数量
    • 增大超参数min_*或是减小max_*将使模型正则化

  • 不稳定性

    • 决策树青睐正交的决策边界（所有分裂都与轴线垂直），这导致它们对训练集的旋转非常敏感。
    • 更概括的说，决策树的主要问题是它们对训练数据中的小变化非常敏感。
    • 限制这种问题的方法之一是使用PCA。
    • 随机森林也可以限制这种不稳定性。

  • 习题摘抄

    • 如果训练集有100万个实例，训练决策树（无约束）大致的深度是多少？

      一个包含m个叶节点的均衡二叉树的深度等于 l o g 2 m log_2m log2​m的四舍五入。通常来说，二元决策树训练到最后大体都是平衡的。如果不加以限制，最后平均每个叶节点一个实例。因此，如果训练集包含一百万个实例，那么决策树深度约等于 l o g 2 ( 1 0 6 ) ≈ 20 log_2(10^6)\approx 20 log2​(106)≈20层。实际上，会更多一些，因为决策树通常不可能完美平衡。

    • 通常来说，子节点的基尼不纯度是高于还是低于父节点？是通常更高/更低？还是永远更高/更低？

      一个节点的基尼不纯度通常比其父节点低。这是通过CART训练算法的成本函数确保的。该算法分裂每个节点的方法，是使其子节点的基尼不纯度的加权之和最小。但是，如果一个子节点的不纯度远小于另一个，那么也有可能使子节点的基尼不纯度比其父节点高，只要那个不纯度更低的子节点能够抵偿这个增加即可。

      举例：

      假设一个节点包含4个A类别的实例和1个B类别的实例，其基尼不纯度等于 1 − 1 5 2 − 4 5 2 = 0.32 1-\frac15^2-\frac45^2=0.32 1−51​2−54​2=0.32。现在我们假设数据使一维的，并且实例的排列顺序如下：A，B，A，A，A。你可以验证，算法将在第二个实例后拆分该节点，从而生成两个子节点所包含的实例分别为A，B和A，A，A。第一个子节点的基尼不纯度为 1 − 1 2 2 − 1 2 2 = 0.5 1-\frac12^2-\frac12^2=0.5 1−21​2−21​2=0.5，比其父节点要高。这是因为第二个子节点是纯的，所以总的加权基尼不纯度等于 2 5 ∗ 0.5 + 3 5 ∗ 0.5 = 0.2 \frac25*0.5+\frac35*0.5=0.2 52​∗0.5+53​∗0.5=0.2低于父节点的基尼不纯度。

    • 如果在包含100万个实例的训练集上训练决策树需要一个小时，那么在包含1000万个实例的训练集上训练决策树，大概需要多长时间？

      决策树的训练复杂度为 O ( n ∗ m l o g ( m ) ) O(n*mlog(m)) O(n∗mlog(m))。所以，如果将训练集大小乘以10，训练时间将乘以

      K = ( n × 10 m × l o g ( 10 m ) ) / ( n × m × l o g ( m ) ) = 10 × l o g ( 10 m ) / l o g ( m ) K=(n \times 10m \times log(10m)) / (n \times m \times log(m))=10 \times log(10m) / log(m) K=(n×10m×log(10m))/(n×m×log(m))=10×log(10m)/log(m)

      如果 m = 1 0 6 m=10^6 m=106，那么 K ≈ 11.7 K \approx 11.7 K≈11.7，所以训练1000万个实例大约需要11.7小时。

    • 如果训练集包含100000个实例，设置presort=True可以加快训练么？

      只有当数据集小于数千个实例时，预处理训练集才可以加速训练。如果包含100000个实例，设置presort=True会显著减慢训练。

  • scipy.stats.mode

    • 在Python中，我们可以用scipy.stats.mode函数寻找数组或者矩阵每行/每列中最常出现成员以及出现的次数 。
    • 参考链接：mode

7. 集成学习和随机森林

  • 投票分类器

    • 使用不同的训练方法训练同样的数据集。

    • from sklearn.ensemble import VotingClassifier：

      voting_clf = VotingClassifier(
    estimators=[
        ('lr', log_clf),
        ('rf', rnd_clf),
        ('svc', svm_clf)
    ],
    voting='hard'
)
voting_clf.fit(X_train, y_train)

  • bagging和pasting

    • 每个预测器使用的算法相同，但是在不同的训练集随机子集上进行训练。

    • 采样时样本放回：bagging(boostrap aggregating，自举汇聚法)，统计学中，放回重新采样称为自助法(bootstrapping)。

    • 采样时样本不放回：pasting。

    • from sklearn.ensemble import BaggingClassifier

      bag_clf = BaggingClassifier(
    DecisionTreeClassifier(), n_estimators=500, max_samples=100, bootstrap=True, n_jobs=-1
)
bag_clf.fit(X_train, y_train)

    • 如果想使用pasting，只需要设置bootstrap=False

    • 集成预测的泛化效果很可能比单独的分类器要好一些：二者偏差相近，但是集成的方差更小。（两边训练集上的错误数量差不多，但是集成的决策边界更规则）

    • 由于自助法给每个预测器的训练子集引入了更高的多样性，所以最后bagging比pasting的偏差略高，但这也意味着预测器之间的关联度更低，所以集成的方差降低。

    • 总之，bagging生成的模型通常更好。

  • 包外评估

    • 对于任意给定的预测器，使用bagging，有些实例可能会被采样多次，而有些实例则可能根本不被采样。

    • BaggingClassifier默认采样m个训练实例，然后放回样本(bootstrap=True)，m是训练集的大小。这意味着对于每个预测器来说，平均只对63%的训练实例进行采样。（随着m增长，这个比率接近 1 − e x p ( − 1 ) ≈ 63.212 1-exp(-1)\approx63.212% 1−exp(−1)≈63.212）。剩余37%未被采样的训练实例成为**包外(oob)**实例。注意，对所有预测其来说，这是不一样的37%。

    • 同个设置oob_score=True自动进行包外评估，通过变量oob_score_可以得到最终的评估分数。

      bag_clf = BaggingClassifier(
    DecisionTreeClassifier(), n_estimators=500, bootstrap=True, n_jobs=-1, oob_score=True
)
bag_clf.fit(X_train, y_train)
bag_clf.oob_score_

    • 每个训练实例的包外决策函数也可以通过变量oob_decision_function_获得。

      bag_clf.oob_decision_function_

  • Random Patches和随机子空间

    • BaggingClassifier也支持对特征进行抽样，这通过两个超参数控制：max_features和bootstrap_features。它们的工作方式跟max_samples和bootstrap相同，只是抽样对象不再是实例，而是特征。因此，每个预测器将用输入特征的随机子集进行训练。
    • 这对于处理高维输入特别有用（例如图像）。对训练实例和特征都进行抽样，被称为Random Patches方法。而保留所有训练实例（即bootstrap=False并且max_samples=1.0）但是对特征进行抽样（即bootstrap_features=True并且/或max_features<1.0），这被称为随机子空间法。

  • 极端随机树（Extra-Trees）

    • 随机森林里单棵树的生长过程中，每个节点在分裂时仅考虑到了一个随机子集所包含的特征。如果我们对每个特征使用随机阈值，而不是搜索得出的最佳阈值（如常规决策树），则可能让决策树生长得更加随机。
    • 这种极端随机的决策树组成的森林，被称为极端随机树（Extra-Trees）。
    • 它也是以更高的偏差换取了更低的方差。
    • 极端随机树训练起来比常规随机森林要快很多，因为在每个节点上找到每个特征的最佳阈值是决策树生长中最耗时的任务之一。
    • from sklearn.ensemble import ExtraTreesClassifier

  • 特征重要性

    • 如果你查看单个决策树会发现，重要的特征更可能出现靠近根节点的位置，而不重要的特征通常出现在靠近叶节点的位置（甚至根本不出现）。
    • 因此可以通过计算一个特征在森林中所有树上的平均深度，可以估算一个特征的重要程度。

  • 提升法（boosting）

    • 提升法（Boosting，假设提升）：是指可以将几个弱学习器结合成一个强学习器的任意集成方法。
    • 大多数boosting的总体思想是循环训练预测器，每一次都对其前序做出一些改正。
    • 可用的提升法有很多，但目前最流行的方法是AdaBoost（自适应提升法，Adaptive Boosting）和梯度提升。

  • AdaBoost（自适应提升法）

    • 新预测器对其前序进行纠正的办法之一，就是更多的关注前序拟合不足的训练实例。从而使新的预测器不断地越来越专注于难缠的问题，这就是AdaBoost使用的技术。

    • 例如，要构建一个AdaBoost分类器，首先需要训练一个基础分类器（比如决策树），用它对训练集进行预测。然后对错误分类的训练实例增加其相对权重，接着，使用这个最新的权重对第二个分类器进行训练，然后再次对训练集进行预测，继续更新权重，并不断循环向前。

    • AdaBoost这种依序循环的学习技术跟梯度下降有一些异曲同工之处，差别只在于——不再是调整单个预测器的参数使成本函数最小化，而是不断在集成中加入预测器，使模型越来越好。

    • 这种依序学习技术有一个重要的缺陷就是无法并行，因为每个预测器只能在前一个预测器训练完成并评估之后才能开始训练。因此，在扩展方面，它的表现不如bagging和pasting方法。

    • 循环过程：计算新预测器的权重，更新实例权重，然后对另一个预测器进行训练。当达到所需数量的预测器，或得到完美的预测器时，算法停止。

    • sklearn使用的时AdaBoost的一个多分类版本，叫做SAMME（基于多类指数损失函数的逐步添加模型）。当只有两个类时，SAMME即等同于AdaBoost。此外，如果预测器可以估算类别概率（即具有predict_proba()方法），sklearn会使用一种SAMME的变体，成为SAMME.R（R代表“Real”），它依赖的是类别概率而不是类别预测，通常表现得更好。

      from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
ada_clf = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1), n_estimators=200, algorithm="SAMME.R", learning_rate=0.5)
ada_clf.fit(X_train, y_train)

    • 如果你的AdaBoost集成过度拟合训练集，你可以试试减少estimator数量，或提高基础estimator的正则化程度。

  • 梯度提升（Gradient Boosting）

    • 跟AdaBoost一样，梯度提升也是逐渐在集成中添加预测器，每一个都对其前序做出改正。不同之处在于，它不是像AdaBoost那样在每个迭代中调整实例权重，而是让新的预测器针对前一个预测器的残差进行拟合。

    • 使用决策树作为基础预测器，叫做梯度提升树（GBDT）或梯度提升回归树（GBRT）。

    • GBDT中的树是回归树（不是分类树），GBDT用来做回归预测，调整后也可以用于分类。

      from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt

# 建立数据
boston = load_boston()
X = boston["data"]
y = boston["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 首先，在训练集上拟合一个DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(max_depth=2)
tree_reg1.fit(X_train, y_train)

# 现在，针对第一个预测器的残差，训练第二个DecisionTreeRegressor
y2 = y_train - tree_reg1.predict(X_train)
tree_reg2 = DecisionTreeRegressor(max_depth=2)
tree_reg2.fit(X_train, y2)

# 然后针对第二个预测器的残差，训练第三个回归器
y3 = y2 - tree_reg2.predict(X_train)
tree_reg3 = DecisionTreeRegressor(max_depth=2)
tree_reg3.fit(X_train, y3)

# 现在，我们有了一个包含3棵树的集成。它将所有树的预测相加，从而对新实例进行预测。
y_pred = sum(tree.predict(X_test) for tree in (tree_reg1, tree_reg2, tree_reg3))

plt.plot(list(range(len(y_pred))), y_pred, 'r', label="pred", alpha=0.5)
plt.plot(list(range(len(y_pred))), y_test, 'b', label="test", alpha=0.5)
plt.legend()

    • 训练GBDT集成有个简单的方法

      • from sklearn.ensemble import GradientBoostingRegressor

        from sklearn.ensemble import GradientBoostingRegressor

gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=3, learning_rate=1.0)
gbrt.fit(X_train, y_train)

      • learning_rate：对每棵树的贡献进行缩放。如果你将其设置为低值，则需要更多的树来拟合训练集，但是预测的泛化效果通常更好。这是一种被称为收缩的正则化技术。如果learning_rate较低，那么estimator太少会导致欠拟合，过多会导致过拟合。

      • 要找到树的最佳数量，可以使用早期停止法。

        • 使用staged_predict()方法：它在训练的每个阶段（一棵树，两棵树…）都对集成的预测返回一个迭代器。

          # 以下代码训练了一个拥有120棵树的GBRT集成，然后测量每个训练阶段的验证误差，从而找到树的最优数量，最后使用最优树数重新训练了一个GBRT集成。

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

X_train, X_val, y_train, y_val = train_test_split(X, y)

gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=120)
gbrt.fit(X_train, y_train)

errors = [mean_squared_error(y_val, y_pred) for y_pred in gbrt.staged_predict(X_val)]
bst_n_estimators = np.argmin(errors)

gbrt_best = GradientBoostingRegressor(max_depth=2, n_estimators=bst_n_estimators)
gbrt_best.fit(X_train, y_train)

print(bst_n_estimators)

        • 实际上，要实现早期停止法，不一定需要先训练大量的树，然后再回头找最优的数字，还可以真的提前停止训练。设置warm_state=True，当fit()方法被调用时，sklearn会保留现有的树，从而允许增量训练。比如以下代码会在验证误差连续5次迭代未改善时，直接停止训练。

          gbrt = GradientBoostingRegressor(max_depth=2, warm_start=True)

min_val_error = float("inf")
error_going_up = 0
for n_estimators in range(1, 120):
    gbrt.n_estimators = n_estimators
    gbrt.fit(X_train, y_train)
    y_pred = gbrt.predict(X_val)
    val_error = mean_squared_error(y_val, y_pred)
    if val_error < min_val_error:
        min_val_error = val_error
        error_going_up = 0
    else:
        error_going_up += 1
        if error_going_up == 5:
            # 早期停止
            break
            
print(val_error)
print(n_estimators)

      • subsample：指定用于训练每棵树的实例的比例。如果subsample=0.25，则每棵树用25%的随机选择的实例进行训练。这也是用更高的偏差换取了更低的方差，同时在相当大的程度上加速了训练。这种技术称为随机梯度提升。

      • loss：梯度提升也可以使用其他成本函数。

  • 堆叠法（stacking，层叠泛化法）

    • 它基于一个简单的思想：与其使用一些简单的函数（比如说硬投票）来聚合集成中所有预测器的预测，我们为什么不训练一个模型来执行这个聚合呢？
    • 训练混合器的常用方法是使用留存集（或者使用折外（out-of-fold）预测也可以。在某些情况下，这才被成为堆叠（stacking），而使用留存集被称为混合（blending）。但是对多数人而言，这二者是同义词。）
    • 参考链接：ensamble之stacking详介以及Python代码实现，详解stacking过程

  • 总结

  • 集成学习主要包括（Bagging，Boosting,Stacking） 众所周知，计算方法分为并行，串行，树行，他们分别对应以上三个集成方法 并行的目的在于学习模型的稳定性 串行的目的在于解决并行中出现的泛化能力差之类问题 而树形即（stacking）的思想是什么呢? 个人给出两点： 1.人解决问题的思维是树形的，将模型树行化符合问题本身的逻辑，精确率和召回率呈稳态正相关 2.stacking使模型的融合更科学化，分层预测的计算结果远优于向量均值化和投票机制。

  • 练习摘抄

    • 硬投票分类器和软投票分类器有什么区别？

      硬投票分类器只是统计每个分类器的投票，然后挑选出得票最多的类别。软投票分类器计算出每个类别的平均估算概率，然后选出概率最高的类别。它比硬投票法的表现更优，因为它给予那些高度自信的投票更高的权重。但是它要求每个分类器都能够估算出类别概率才可以正常工作。（例如，sklearn中的SVM分类器必须要设置probability=True）

    • 是否可以通过在多个服务器上并行来加速bagging集成的训练？pasting集成呢？boosting集成呢？随机森林或stacking集成呢？

      1. 对于bagging集成来说，将其分布在多个服务器上能够有效加速训练过程，因为集成中的每个预测器都是独立工作的。

      2. 同理，对于pasting集成和随机森林来说也是如此。

      3. 但是，boosting集成的每个预测器都是基于前序的结果，因此训练过程必须是有序的，将其分布在多个服务器上毫无意义。

      4. 对于stacking集成来说，某个指定层的预测器之间彼此独立，因而可以在多台服务器上并行训练，但是某一层的预测器只能在其前一层的预测器全部训练完成之后，才能开始训练。

    • 包外评估的好处是什么?

      包外评估可以对bagging集成中的每个预测器使用其未经训练的实例进行评估。不需要额外的验证集，就可以对集成实施相当公正的评估。所以，如果训练使用的实例越多，集成的性能可以略有提升。

    • 是什么让极端随机树比一般随机森林更加随机？这部分增加的随机性有什么用？极端随机树比一般随机森林快还是慢？

      随机森林在生长过程中，每个节点的分裂仅考虑了特征的一个随机子集。极限随机树也是如此，它甚至走得更远：常规随机树会搜索出特征的最佳阈值，极限随机树直接对每个特征使用随机阈值。这种极限随机性就像是一种正则化的形式：如果随机森林对训练数据出现过拟合，那么极限随机树可能执行效果更好。更甚的是，极限随机树不需要计算最佳阈值，因此它训练起来比随机森林快得多。但是，在做预测的时候，相比随机森林它不快也不慢。

    • 如果你的AdaBoost集成队训练数据拟合不足，你应该调整哪些超参数？怎么调整？

      1. 提升估算器的数量
      2. 降低基础估算器的正则化超参数
      3. 略微提升学习率

    • 如果你的梯度提升集成对训练集过度拟合，你应该提升还是降低学习率？

      降低学习率，也可以通过早停法来寻找合适的预测器数量（可能是因为预测器太多）。

8. 降维

  • 数据降维的两种主要方法

    • 投影
    • 流形学习
      • 流形假设：也称为流形假说，认为大多数现实世界的高维度数据集存在一个低维度的流形来重新表示。这个假设通常是凭经验观察的。
      • 流形假设通常还伴随着一个隐含的假设：如果能用低维空间的流形表示，手头的任务（例如分类或者回归）将变得更简单。

  • PCA

    • 主成分分析（PCA）是迄今为止最流行的降维算法。它先是识别出最接近数据的超平面，然后将数据投影其上。

    • 比较原始数据集与其轴上的投影之间的均方距离，使这个均方距离最小的轴使最合理的选择。这也正是PCA背后的简单思想。

    • 奇异值分解（SVD）

      import numpy as np

X = np.random.random((50, 2))
X_centered = X - X.mean(axis=0)
U, s, V = np.linalg.svd(X_centered)
c1 = V.T[:, 0]
c2 = V.T[:, 1]

W2 = V.T[:, :1]
W2D = X_centered.dot(W2)

    • PCA实战

      from sklearn.decomposition import PCA

pca = PCA(n_components=1)
X2D = pca.fit_transform(X)

      • components_：访问主成分（它包含的主成分使水平向量）。举例来说，第一个主成分即等于

        pca.components_.T[:, 0]

      • explained_variance_ratio_：方差解释率。它表示每个主成分轴对整个数据集方差的贡献度。

      • inverse_transform()：将压缩后的数据解压缩回到原来的shape。原始数据和重建数据（压缩之后解压缩）之间的均方距离成为重建误差。

    • 选择正确数量的维度：

      • 设置n_components=d，若d是整数，则设置为降维后的维度数；若d是小数，则表示希望保留的方差比。
      • 还可以将解释方差绘制关于维度数量的函数（绘制np.cumsum即可）。曲线通常都会有一个拐点，说明方差停止快速增长。你可以将其视为数据集的本征维数。

    • 增量PCA（IPCA）

      • 增量主成分分析

      • 可以将训练集分成一个个小批量，一次给IPCA

        import numpy as np
from sklearn.decomposition import IncrementalPCA
from sklearn.datasets import fetch_mldata

n_batches = 100
mnist = fetch_mldata('MNIST original')
X_mnist = mnist["data"]

inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_mnist, n_batches):
	inc_pca.partial_fit(X_batch)
X_mnist_reduced = inc_pca.transform(X_mnist)

      • 还可以使用Numpy的memmap类，它允许你巧妙地操控一个存储在磁盘二进制文件的大型数组，就好似它也完全在内存里一样，而这个类（memmap）仅在需要时加载内存中需要的数据。

      • 内存映射，当需要存取一个很大的文件里面的小部分的数据的时候，读入整个文件显然是非常的浪费资源的。于是要使用到内存映射的方法。

      • numpy中的numpy.memmap函数的用法

        X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n))
batch_size = m // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mm)

    • 随机PCA

      • 这是一个随机算法，可以快速找到前d个主成分的近似值。
      • 它的计算复杂度是 O ( m × d 2 ) + O ( d 3 ) O(m\times d^2) + O(d^3) O(m×d2)+O(d3)，而不是 O ( m × n 2 ) + O ( n 3 ) O(m \times n^2) + O(n^3) O(m×n2)+O(n3)。
      • 所以当d远小于n时，它比前面提到的算法要快得多。
      • 使用时，设置PCA中的参数svd_solver=“randomized”

  • 核主成分分析（kPCA）

    • 将核技巧应用于PCA，使复杂的非线性投影降维成为可能。

    • 它擅长在投影后保留实例的集群，有时甚至也能展开近似于一个扭曲流形的数据集。

      from sklearn.decomposition import KernelPCA

rbf_pca = KernelPCA(n_components=2, kernel='rbf', gamma=0.04)
X_reduced = rbf_pca.fit_transform(X)

    • 选择核函数核调整超参数

      • 使用网格搜索，kPCA搭配分类器（逻辑回归等），来找到使任务性能最佳的核和超参数。

        from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import KernelPCA
from sklearn.pipeline import Pipeline
import numpy as np

clf = Pipeline([
    ("kpca", KernelPCA(n_components=2)),
    ("log_reg", LogisticRegression())
])

param_grid = [{
           
    "kpca__gamma": np.linspace(0.03, 0.05, 10),
    "kpca__kernel": ["rbf", "sigmoid"]
}]

grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)

      • 重建原像

        • 还有一种完全不受监督的方法，就是选择重建误差最低的核和超参数。

        • 如果我们对一个已经降维的实例进行线性PCA逆转换，重建的点将存在于特征空间，而不是原始空间中。而这里特征空间是无限维度的，所以我们无法计算出重建点，因此也无法计算出真实的重建误差。

        • 我们可以在原始空间中找到一个点，使其映射接近于重建点。这被称为重建原像。

        • 一旦有了这个原像，你就可以测量它到原始实例的平方距离。最后，便可以选择使这个重建原像误差最小化的核和超参数。

        • **执行重建的方法：**训练一个监督式回归模型，以投影后的实例作为训练集，并以原始实例作为目标。（设置KernelPCA中的fit_inverse_transform=True）

          rbf_pca = KernelPCA(n_components=2, kernel="rbf", gamma=0.0433, fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)

          计算重建原像误差：

          from sklearn.metrics import mean_squared_error
mean_squared_error(X, X_preimage)

        • 现在，你可以使用交叉验证的网格搜索，来寻找使这个原像重建误差最小的核和超参数。

  • 局部线性嵌入（LLE，Locally Linear Embedding）

    • 局部线性嵌入使另一种非常强大的非线性降维（NLDR）技术，不像之前的算法依赖于投影，它是一种流形学习技术。

    • LLE首先测量每个算法如何与其最近的邻居线性相关，然后为训练集寻找一个能最大程度保留这些局部关系的低维表示。

    • 这使得它特别擅长展开弯曲的流形，特别使没有太多噪声时。

      from sklearn.manifold import LocallyLinearEmbedding

lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
X_reduced = lle.fit_transform(X)

    • 计算复杂度：

      • 寻找k个最近邻为： O ( m l o g ( m ) n l o g ( k ) ) O(m log(m)n log(k)) O(mlog(m)nlog(k))
      • 优化权重为： O ( m n k 3 ) O(mnk^3) O(mnk3)
      • 构建低维表示： O ( d m 2 ) O(dm^2) O(dm2)
      • 很不幸，最后一个表达式里的 m 2 m^2 m2说明这个算法很难扩展应用到大型数据集。

  • 其他降维技巧

    • 多维缩放（MDS）：保持实例之间的距离，降低维度。
    • 等度量映射（Isomap）：将每个实例与其最近的邻居连接起来，创建链接图形，然后保留实例之间的这个测地距离，降低维度。图中两个节点之间的测地距离是两个节点之间最短路径上的节点数。
    • t-分布随机近邻嵌入（t-SNE，T-distributed Stochastic Neighbor Embedding）：在降低维度时，试图让相近的实例彼此靠近，不相似的实例彼此远离。它主要用于可视化，尤其是将高维空间中的实例集群可视化。
    • 线性判别式分析（Linear Discriminant Analysis，LDA）：实际上是一种分类算法，但是在训练过程中，它会学习类别之间最有区别的轴，而这个轴正好可以用来定义投影数据的超平面。这样做的好处在于投影上的类别之间会尽可能的分开，所以在运行其他分类算法——比如SVM分类器之前，LDA是一个不错的降维手段。

  • 练习摘抄

    • 降低数据集维度的主要动机是什么？有什么主要弊端？

      降维的主要动机是：

      1. 为了加速后续的训练算法（在某些情况下，也可能是为了消除噪声和冗余特征，使训练算法性能更好）。
      2. 为了将数据可视化，并从中获得洞悉，了解重要的特征。
      3. 只是为了节省空间（压缩）

      主要的弊端使：

      1. 丢失部分信息，可能后续训练算法的性能降低
      2. 可能使计算密集型的
      3. 为机器学习流水线增条了些许复杂度
      4. 转换后的特征往往难以解释

    • 什么是维度的诅咒？

      维度的诅咒是指寻多在低维空间中不存在的问题，在高维空间中发生。在机器学习领域，一个常见的现象是随机抽样的高维向量通常非常稀疏，提升了过度拟合的风险，同时也使得在没有充足训练数据的情况下，要识别数据中的模式非常困难。

    • 一旦数据集被降维，是否还有可能逆转？如果有，怎么做？如果没有，为什么？

      一旦使用我们讨论的任意算法减少了数据集的维度，几乎不可能再将操作完美的逆转，因为在降维过程中必然丢失了一部分信息。虽然有一些算法（例如PCA）拥有简单的逆转换过程，可以重建出与原始数据集相似的数据集，但是也有一些算法不能实现逆转（例如t-SNE）。

    • PCA可以用来给高度非线性数据集降维么？

      对大多数数据集来说，PCA可以用来进行显著降维，即便是高度非线性的数据集，因为它至少可以消除无用的维度。但是如果不存在无用的维度（例如瑞士卷），那么使用PCA降维将会损失太多信息。你希望的是将瑞士卷展开，而不是将其压扁。

    • 常规PCA，增量PCA，随机PCA及核PCA各适用于何种情况？

      • 常规PCA是默认选择，但是它仅适用于内存足够处理训练集的时候。
      • 增量PCA对于内存无法支持的大型数据集非常有用，当时它比常规PCA要来得慢一些，所以如果内存能够支持，还是应该使用常规PCA。当你需要随时应用PCA来处理每次新增的实例时，增量PCA对于在线任务同样有用。
      • 当你想大大降低维度数量，并且内存足够支持数据集时，使用随机PCA非常有效。它比常规PCA快得多。
      • 最后对于非线性数据集，使用核化PCA行之有效。

    • 如何在你的数据集上评估降维算法的性能？

      • 直观来说，如果降维算法能够消除许多维度并且不会丢失太多信息，那么这就算是一个好的降维算法。
      • 进行衡量的方法之一是应用逆转换然后测量重建误差。
      • 然而并不是所有的降维算法都提供了逆转换。还有一种选择，如果你将降维当作一个预处理过程，用在其他机器学习算法（比如随机森林分类器）之前，那么可以通过简单的测量第二个算法的性能来进行评估。如果降维过程没有损失太多信息，那么第二个算法的性能应该跟使用原始数据集一样好。

    • 链接两个不同的降维算法有意义吗？

      链接两个不同的降维算法绝对是有意义的。常见的例子是使用PCA快速去除大量无用的维度，然后应用另一种更慢的降维算法，如LLE。这样两步走的策略产生的结果可能与仅使用LLE相同，但是时间要短得多。

9. 运行TensorFlow

  • 创建一个计算图并在会话中执行

    x = tf.Variable(3, name="x")
y = tf.Variable(4, name="y")
f = x*x*y + y + 2

sess = tf.Session()
sess.run(x.initializer)
sess.run(y.initializer)
result = sess.run(f)
print(result)
sess.close()

# 每次重复sess.run()看起来有些笨拙，好在有更好的方式
with tf.Session() as sess:
    x.initializer.run()
    y.initializer.run()
    result = f.eval()
    print(result)

    • 其中x.initializer.run()等价于tf.get_default_session().run(x.initializer)

    • 同样，f.eval()等价于tf.get_default_session().run(f)

    • 除了手工为每个变量调用初始化器之外，还可以使用global_variables_initializer()函数来完成同样的动作。注意：这个操作并不会立刻做初始化，它只是在图中创建了一个节点，这个节点会在会话执行时初始化所有变量。

      init = tf.global_variables_initializer()

with tf.Session() as sess:
    init.run()
    result = f.eval()
    print(result)

    • 在Jupyter或者Python shell中，可以创建一个InteractiveSession。它和常规会话的不同之处在于InteractiveSession在创建时会将自己设置为默认会话，因此你无须使用with块（不过需要在结束之后手动关闭会话）。

      sess = tf.InteractiveSession()
init.run()
result = f.eval()
print(result)
sess.close()

  • 管理图

    • 你创建的所有节点都会自动添加到默认图上

      x1 = tf.Variable(1)
x1.graph is tf.get_default_graph()

    • 有时候你可能想要管理多个互不依赖的图。可以创建一个新的图，然后用with块临时将它设置为默认图

      graph = tf.Graph()
with graph.as_default():
    x2 = tf.Variable(2)

x2.graph is graph
x2.graph is tf.get_default_graph()

    • 在Jupyter中，做实验时你经常会多次执行同一条命令。这样可能会在同一个图上添加了很多重复的节点。

      • 一种做法是重启Jupyter内核
      • 更方便的做法是通过tf.reset_default_graph()来重置默认图

  • 节点值的生命周期

    w = tf.constant(3)
x = w + 2
y = x + 5
z = x * 3

with tf.Session() as sess:
    print(y.eval())
    print(z.eval())

    • TensorFlow不会重复用上一步求值的w和x的结果。简而言之，w和x的值会被计算两次。

    • 在图的每次执行间，所有节点值都会被丢弃，但是变量的值不会，因为变量的值是由会话维护的（队列和阅读器也会维护一些状态）。变量的生命周期从初始化器的执行开始，到关闭会话才结束。

    • 对于上述代码，如果你不希望对y和z重复求值，那么必须告诉TensorFlow在一次图执行中就完成y和z的求值

      with tf.Session() as sess:
    y_val, z_val = sess.run([y, z])
    print(y_val)
    print(z_val)

    • 在单进程的TensorFlow中，即使它们共享同一个计算图，多个会话之间仍然互相隔离，不共享任何状态（每个会话对每个变量都有自己的拷贝）。

    • 对于分布式TensorFlow，变量值保存在每个服务器上，而不是会话中，所以多个会话可以共享同一变量。

  • TensorFlow中的线性回归

    import numpy as np
from sklearn.datasets import fetch_california_housing

housing = fetch_california_housing()
m, n = housing.data.shape
housing_data_plus_bias = np.c_[np.ones((m, 1)), housing.data]

X = tf.constant(housing_data_plus_bias, dtype=tf.float32, name="X")
y = tf.constant(housing.target.reshape(-1, 1), dtype=tf.float32, name="y")
XT = tf.transpose(X)
theta = tf.matmul(tf.matmul(tf.matrix_inverse(tf.matmul(XT, X)), XT), y)

with tf.Session() as sess:
    theta_value = theta.eval()
    print(theta_value)

  • 实现梯度下降

    • 手动计算梯度

      n_epochs = 1000
learning_rate = 0.01

X = tf.constant(scaled_housing_data_plus_bias, dtype=tf.float32, name="X")
y = tf.constant(housing.target.reshape(-1, 1), dtype=tf.float32, name="y")
theta = tf.Variable(tf.random_uniform([n+1, 1], -1.0, 1.0), name="theta")
y_pred = tf.matmul(X, theta, name="perdictions")
error = y_pred - y
mse = tf.reduce_mean(tf.square(error), name="mse")
gradients = 2/m * tf.matmul(tf.transpose(X), error)
training_op = tf.assign(theta, theta - learning_rate * gradients)

init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    
    for epoch in range(n_epochs):
        if epoch % 100 == 0:
            print("Epoch", epoch, "MSE = ", mse.eval())
        sess.run(training_op)
    
    best_theta = theta.eval()
      • 函数random_uniform()会在图中创建一个节点，这个节点会生成一个张量。函数会根据传入的形状和值域来生成随机值来填充这个张量，这和Numpy的rand()函数很相似。
      • 函数assign()创建一个为变量赋值的节点。这里，它实现了批量梯度下降。

    • 使用自动微分

      • TensorFlow的autodiff功能可以自动而且高效的算出梯度。只需要把上述例子中的对gradients的赋值的语句换成下面的代码即可。

        gradients = tf.gradients(mse, [theta])[0]

      • gradients()函数接受一个操作符（这里是mse）和一个参数列表（这里是theta）作为参数，然后它会创建一个操作符的列表来计算每个变量的梯度。所以梯度节点将计算MSE相对于theta的梯度向量。

      • TensorFlow使用了反向的autodiff算法，它非常适用于有多个输入和少量输出的场景，在神经网络中这种场景非常常见。它只需要 n o u t p u t s + 1 n_{outputs}+1 noutputs​+1次遍历，就可以求出所有输出相对于输入的偏导。

      • 四种自动计算梯度的主要方法

        方法 精确度 是否支持任意代码 备注
        数值微分 低 是 实现琐碎
        符号微分 高 否 会构建一个完全不同的图
        前向自动微分 高 是 基于二元树
        反向自动微分 高 是 由TensorFlow实现

    • 实现优化器

      • TensorFlow会帮你计算梯度，不过它还提供更容易的方法：它内置了很多的优化器，其中就包含梯度下降优化器。你只需要把上面对gradients=…和training_op=…赋值的语句修改成下面的代码即可：

        optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(mse)

      • 动量优化器（比梯度下降优化器的收敛速度快很多）

        optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9)

  • 给训练算法提供数据

    • 占位符节点

      A = tf.placeholder(tf.float32, shape=(None, 3))
B = A + 5
with tf.Session() as sess:
    B_val_1 = B.eval(feed_dict={
         A: [[1, 2, 3]]})
    B_val_2 = B.eval(feed_dict={
         A: [[4, 5, 6], [7, 8, 9]]})
    print(B_val_1)
    print(B_val_2)

    • Mini-batch Gradient Descent

      learning_rate = 0.01

X = tf.placeholder(tf.float32, shape=(None, n + 1), name="X")
y = tf.placeholder(tf.float32, shape=(None, 1), name="y")

theta = tf.Variable(tf.random_uniform([n + 1, 1], -1.0, 1.0, seed=42), name="theta")
y_pred = tf.matmul(X, theta, name="predictions")
error = y_pred - y
mse = tf.reduce_mean(tf.square(error), name="mse")
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(mse)

init = tf.global_variables_initializer()

n_epochs = 10
batch_size = 100
n_batches = int(np.ceil(m / batch_size))

def fetch_batch(epoch, batch_index, batch_size):
    np.random.seed(epoch * n_batches + batch_index)  # not shown in the book
    indices = np.random.randint(m, size=batch_size)  # not shown
    X_batch = scaled_housing_data_plus_bias[indices] # not shown
    y_batch = housing.target.reshape(-1, 1)[indices] # not shown
    return X_batch, y_batch

with tf.Session() as sess:
    sess.run(init)

    for epoch in range(n_epochs):
        for batch_index in range(n_batches):
            X_batch, y_batch = fetch_batch(epoch, batch_index, batch_size)
            sess.run(training_op, feed_dict={
         X: X_batch, y: y_batch})

    best_theta = theta.eval()

  • 保存和恢复模型

    • 保存模型：saver = tf.train.Saver()

      n_epochs = 1000                                                                       # not shown in the book
learning_rate = 0.01                                                                  # not shown

X = tf.constant(scaled_housing_data_plus_bias, dtype=tf.float32, name="X")            # not shown
y = tf.constant(housing.target.reshape(-1, 1), dtype=tf.float32, name="y")            # not shown
theta = tf.Variable(tf.random_uniform([n + 1, 1], -1.0, 1.0, seed=42), name="theta")
y_pred = tf.matmul(X, theta, name="predictions")                                      # not shown
error = y_pred - y                                                                    # not shown
mse = tf.reduce_mean(tf.square(error), name="mse")                                    # not shown
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)            # not shown
training_op = optimizer.minimize(mse)                                                 # not shown

init = tf.global_variables_initializer()
saver = tf.train.Saver()

with tf.Session() as sess:
    sess.run(init)

    for epoch in range(n_epochs):
        if epoch % 100 == 0:
            print("Epoch", epoch, "MSE =", mse.eval())                                # not shown
            save_path = saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model.ckpt")
        sess.run(training_op)
    
    best_theta = theta.eval()
    save_path = saver.save(sess, "D:/Python3Space/BookStudy/book4/model/tmp/my_model_final.ckpt")

    • 恢复模型：恢复模型同样简单，与之前一样，在构造期末尾创建一个Saver节点，不过在执行期开始的时候，不是用init节点来初始化变量，而是调用Saver对象上的restore()方法。

      with tf.Session() as sess:
    saver.restore(sess, "D:/Python3Space/BookStudy/book4/model/tmp/my_model_final.ckpt")
    best_theta_restored = theta.eval() # not shown in the book
    print(best_theta_restored)

    • 默认的，Saver会按照变量名来保留和恢复变量，不过如果你想做更多的控制，也可以在保存和恢复时自己指定名称。比如，在下面的代码中，Saver只会保存theta，并将其命名为weights：

      saver = tf.train.Saver({"weights": theta})

  • 用TensorBoard来可视化图和训练曲线

    • 开启TensorBoard：tensorboard --logdir tf_logs/

      from datetime import datetime

now = datetime.utcnow().strftime("%Y%m%d%H%M%S")
root_logdir = "D:/Python3Space/BookStudy/book4/model/tf_logs"
logdir = "{}/run-{}/".format(root_logdir, now)

n_epochs = 1000
learning_rate = 0.01

X = tf.placeholder(tf.float32, shape=(None, n + 1), name="X")
y = tf.placeholder(tf.float32, shape=(None, 1), name="y")
theta = tf.Variable(tf.random_uniform([n + 1, 1], -1.0, 1.0, seed=42), name="theta")
y_pred = tf.matmul(X, theta, name="predictions")
error = y_pred - y
mse = tf.reduce_mean(tf.square(error), name="mse")
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(mse)

init = tf.global_variables_initializer()

mse_summary = tf.summary.scalar('MSE', mse)
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph())

n_epochs = 10
batch_size = 100
n_batches = int(np.ceil(m / batch_size))

with tf.Session() as sess:                                                        # not shown in the book
    sess.run(init)                                                                # not shown

    for epoch in range(n_epochs):                                                 # not shown
        for batch_index in range(n_batches):
            X_batch, y_batch = fetch_batch(epoch, batch_index, batch_size)
            if batch_index % 10 == 0:
                summary_str = mse_summary.eval(feed_dict={
         X: X_batch, y: y_batch})
                step = epoch * n_batches + batch_index
                file_writer.add_summary(summary_str, step)
            sess.run(training_op, feed_dict={
         X: X_batch, y: y_batch})

    best_theta = theta.eval()                                                     # not shown

file_writer.close()

  • 命名作用域

    reset_graph()

now = datetime.utcnow().strftime("%Y%m%d%H%M%S")
root_logdir = "tf_logs"
logdir = "{}/run-{}/".format(root_logdir, now)

n_epochs = 1000
learning_rate = 0.01

X = tf.placeholder(tf.float32, shape=(None, n + 1), name="X")
y = tf.placeholder(tf.float32, shape=(None, 1), name="y")
theta = tf.Variable(tf.random_uniform([n + 1, 1], -1.0, 1.0, seed=42), name="theta")
y_pred = tf.matmul(X, theta, name="predictions")

with tf.name_scope("loss") as scope:
    error = y_pred - y
    mse = tf.reduce_mean(tf.square(error), name="mse")

optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(mse)

init = tf.global_variables_initializer()

mse_summary = tf.summary.scalar('MSE', mse)
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph())

n_epochs = 10
batch_size = 100
n_batches = int(np.ceil(m / batch_size))

with tf.Session() as sess:
    sess.run(init)

    for epoch in range(n_epochs):
        for batch_index in range(n_batches):
            X_batch, y_batch = fetch_batch(epoch, batch_index, batch_size)
            if batch_index % 10 == 0:
                summary_str = mse_summary.eval(feed_dict={
       X: X_batch, y: y_batch})
                step = epoch * n_batches + batch_index
                file_writer.add_summary(summary_str, step)
            sess.run(training_op, feed_dict={
       X: X_batch, y: y_batch})

    best_theta = theta.eval()

file_writer.flush()
file_writer.close()
print("Best theta:")
print(best_theta)
print(error.op.name)
print(mse.op.name)

  • 模块化

    • 一段错误的代码，这段代码中包含了一个cut-and-paste的错误

      import tensorflow as tf
import numpy as np

n_features = 3
X = tf.placeholder(tf.float32, shape=(None, n_features), name="X")

w1 = tf.Variable(tf.random_normal((n_features, 1)), name="weights1")
w2 = tf.Variable(tf.random_normal((n_features, 1)), name="weights2")
b1 = tf.Variable(0.0, name="bias1")
b2 = tf.Variable(0.0, name="bias2")

z1 = tf.add(tf.matmul(X, w1), b1, name="z1")
z2 = tf.add(tf.matmul(X, w2), b2, name="z2")

relu1 = tf.maximum(z1, 0., name="relu1")
relu2 = tf.maximum(z1, 0., name="relu2")

output = tf.add(relu1, relu2, name="output")

    • TensorFlow会让你保持DRY（Don’t Repeat Yourself，不要重复自己）原则：用一个函数来构建ReLU。

      def reset_graph(seed=42):
    tf.reset_default_graph()
    tf.set_random_seed(seed)
    np.random.seed(seed)

def relu(X):
    with tf.name_scope("relu"):
        w_shape = (int(X.get_shape()[1]), 1)
        w = tf.Variable(tf.random_normal(w_shape), name="weights")
        b = tf.Variable(0.0, name="bias")
        z = tf.add(tf.matmul(X, w), b, name="z")
        return tf.maximum(z, 0., name="relu")
    
reset_graph()
n_features = 3
X = tf.placeholder(tf.float32, shape=(None, n_features), name="X")
relus = [relu(X) for i in range(5)]
output = tf.add_n(relus, name="output")

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    result = output.eval(feed_dict={
         X: [[1, 2, 3], [4, 5, 6]]})
    print(result)
    
file_writer.close()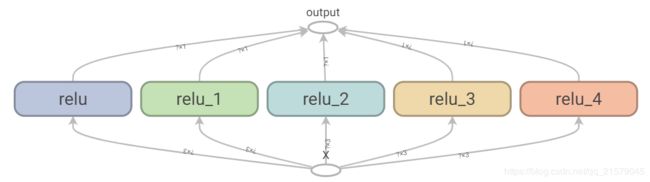

      img

  • 共享变量

    • 如果你想在图的不同组建中共享变量：最简单的做法是先创建，然后将其作为参数传递给需要它的函数。

    • TensorFlow提供另外一个选择，可以让代码更加清晰，也更加模块化。

      • 如果共享变量不存在，该方法先通过get_variable()函数创建共享变量；如果已经存在了，就复用该共享变量。期望的行为通过当前variable_scope()的一个属性来控制（创建或者复用）。

        with tf.variable_scope("relu"):
    threshold = tf.get_variable("threshold", shape=(), initializer=tf.constant_initializer(0.0))

      • 注意，如果这个变量之前已经被get_variable()调用创建过，这里会抛出一个一场。这种机制避免由于误操作而复用变量。

      • 如果要复用一个变量，需要通过设置变量作用域reuse属性为True来显示地实现（在这里，不必指定形状或初始化器）。

        with tf.variable_scope("relu", reuse=True):
    threshold = tf.get_variable("threshold")

      • 这段代码会获取既有的“relu/threshold”变量，如果该变量不存在，或者在调用get_variable()时没有创建成功，那么会抛出一个异常。

      • 另一种方式是，在调用作用域的reuse_variables()方法块中设置reuse属性为True。

        with tf.variable_scope("relu") as scope:
    scope.reuse_variables()
    threshold = tf.get_variable("threshold")

      • 一旦reuse属性设置为True之后，在该块中就不能再设置为False了。另外，如果在块中定义了另外的变量作用域，它们会自动继承resue=True。最后，只有通过get_variable()创建的变量才可以用这种方式进行复用。

    • 现在你已经看到了所有能让relu()函数无须传入参数就访问threshold变量的方法了：

      reset_graph()

def relu(X):
    with tf.variable_scope("relu", reuse=True):
        threshold = tf.get_variable("threshold")
        w_shape = int(X.get_shape()[1]), 1                          # not shown
        w = tf.Variable(tf.random_normal(w_shape), name="weights")  # not shown
        b = tf.Variable(0.0, name="bias")                           # not shown
        z = tf.add(tf.matmul(X, w), b, name="z")                    # not shown
        return tf.maximum(z, threshold, name="max")

X = tf.placeholder(tf.float32, shape=(None, n_features), name="X")
with tf.variable_scope("relu"):
    threshold = tf.get_variable("threshold", shape=(),
                                initializer=tf.constant_initializer(0.0))
relus = [relu(X) for relu_index in range(5)]
output = tf.add_n(relus, name="output")

file_writer = tf.summary.FileWriter("D:/李添的数据哦！！！/BookStudy/book4/model/logs/relu6", tf.get_default_graph())
file_writer.close()

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    result = output.eval(feed_dict={
         X: [[1, 2, 3], [4, 5, 6]]})
    print(result)

    • 通过get_variable()创建的变量总是以它们的variable_scope作为前缀来命名的（比如“relu/threshold”），对于其它节点（包括通过tf.Variable()创建的变量）变量作用域的行为就好像是一个新的作用域。具体来说，如果一个命名作用域有一个已经创建了的变量名，那么就会加上一个后缀以保证其唯一性。比如，上面的例子中的所有变量（除了threshold变量）都有一个“relu_1”到“relu_5”的前缀。

      img

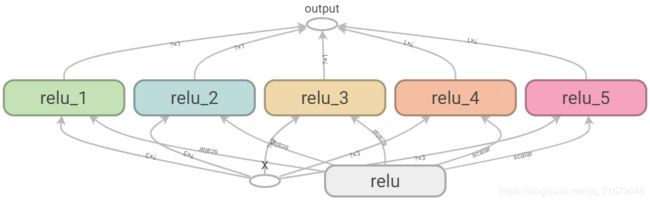
    • 遗憾的是，threshold变量必须定义在relu()函数之外，其他所有的ReLU代码都在内部。要解决这个问题，下面的代码在relu()函数第一次调用时创建了threshold变量，并在后续的调用中复用。现在relu()函数无须关注命名作用域或者变量共享问题，它只需要调用get_variable()，来创建或者复用threshold变量（无需关心到底是创建还是复用）。剩下的代码调用了relu()5次，确保第一次调用时将reuse设置为False，后续的调用将reuse设置为True。

      img

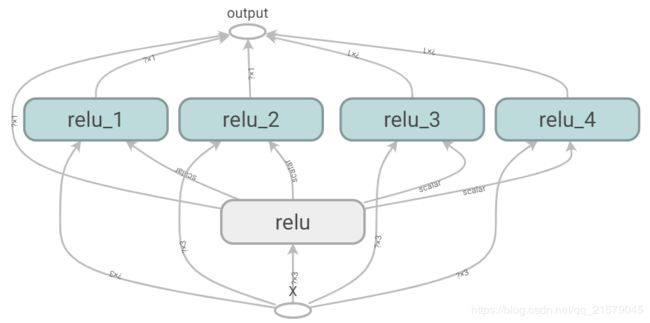
    • 结果跟之前的略有不同，因为共享变量在第一个ReLU中。

    • 方法1：

      reset_graph()

def relu(X):
    with tf.variable_scope("relu"):
        threshold = tf.get_variable("threshold", shape=(), initializer=tf.constant_initializer(0.0))
        w_shape = (int(X.get_shape()[1]), 1)
        w = tf.Variable(tf.random_normal(w_shape), name="weights")
        b = tf.Variable(0.0, name="bias")
        z = tf.add(tf.matmul(X, w), b, name="z")
        return tf.maximum(z, threshold, name="max")

X = tf.placeholder(tf.float32, shape=(None, n_features), name="X")
with tf.variable_scope("", default_name="") as scope:
    first_relu = relu(X)     # create the shared variable
    scope.reuse_variables()  # then reuse it
    relus = [first_relu] + [relu(X) for i in range(4)]
output = tf.add_n(relus, name="output")

file_writer = tf.summary.FileWriter("D:/李添的数据哦！！！/BookStudy/book4/model/logs/relu8", tf.get_default_graph())
file_writer.close()

with tf.Session() as sess:
  sess.run(tf.global_variables_initializer())
    result = output.eval(feed_dict={
         X: [[1, 2, 3], [4, 5, 6]]})
  print(result)

  • 方法2：

    ```python
reset_graph()

def relu(X):
    threshold = tf.get_variable("threshold", shape=(),
                                initializer=tf.constant_initializer(0.0))
    w_shape = (int(X.get_shape()[1]), 1)                        # not shown in the book
  w = tf.Variable(tf.random_normal(w_shape), name="weights")  # not shown
    b = tf.Variable(0.0, name="bias")                           # not shown
    z = tf.add(tf.matmul(X, w), b, name="z")                    # not shown
    return tf.maximum(z, threshold, name="max")

X = tf.placeholder(tf.float32, shape=(None, n_features), name="X")
relus = []

    for relu_index in range(5):
    with tf.variable_scope(“relu”, reuse=(relu_index >= 1)) as scope:
    relus.append(relu(X))
    output = tf.add_n(relus, name=“output”)

    file_writer = tf.summary.FileWriter("D:/李添的数据哦！！！/BookStudy/book4/model/logs/relu9", tf.get_default_graph())
file_writer.close()

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    result = output.eval(feed_dict={X: [[1, 2, 3], [4, 5, 6]]})
    print(result)
```

  • 练习摘抄

    • 语句a_val, b_val = a.eval(session=sess), b.eval(session=sess)和a_val, b_val = sess.run([a, b])等价吗？

      不等价。第一条语句会运行两次（第一次计算a，第二次计算b），而第二条语句只运行一次。如果这些操作（或者它们依赖的操作）中的任意一个具有副作用（比如，修改一个变量，向队列中插入一条记录，或者读取一个文件等），那么效果就会不同。如果操作没有副作用，那么语句会返回同样的结果，不过第二条语句会比第一条快。

    • 假设你创建了一个包含变量w的图，然后在两个线程中分别启动一个会话，两个线程都使用了图g，每个会话会有自己对w变量的拷贝，还是会共享变量？

      在本地TensorFlow中，会话用来管理变量的值，如果你创建了一个包含变量w的图g，然后启动两个线程，并在每个线程中打开一个本地的会话，这两个线程使用同一个图g，那么每个会话会拥有自己的w的拷贝。如果在分布式的TensorFlow中，变量的值则存储在由集群管理的容器中，如果两个会话连接了同一个集群，并使用同一个容器，那么它们会共享变量w。

    • 变量何时被初始化，又在何时被销毁？

      变量在调用其初始化器的时候被初始化，在会话结束的时候被销毁。在分布式TensorFlow中，变量存活于集群上的容器中，所以关闭一个会话不会销毁变量。要销毁一个变量，你需要清空它所在的容器。

    • 占位符和变量的区别是什么？

      • 变量和占位符完全不同。
      • 变量是包含一个值的操作。你执行一个变量，它会返回对应的值。在执行之前，你需要初始化变量。你可以修改变量的值（比如，通过使用赋值操作）。变量有状态：在连续运行图时，变量保持相同的值。通常它被用作保存模型的参数，不过也可以用作其他用途（比如，对全局训练的步数进行计数）。
      • 占位符则只能做很少的事儿：它们只有其所代表的张量的类型和形状的信息，但没有值。事实上，如果你要对一个依赖于占位符的操作进行求值，你必须先为其传值（通过feed_dict），否则你会得到一个异常。占位符通常在被用作在执行期为训练或者测试数据传值。在将值传递给赋值节点以更改变量的值时（例如，模型的权重），占位符也很有用。

    • 在执行期，你如何为一个变量设置任意的值？

      你可以在构造一个图时指定变量的初始值，它会在后边的执行期运行变量的初始化器的时候被初始化。如果你想在执行期修改变量的值，那么最简单的方法是使用tf.assign函数创建一个赋值节点（在图的构造器），将变量和一个占位符传入作为参数。这样，你可以在执行期运行赋值操作来为变量传入新值。

    • 反向模式autodiff需要多少次遍历图形才能计算10个变量的成本函数的梯度？正向模式autodiff怎么样？符号微分呢？

      要计算任意数量变量的成本函数的梯度，反向模式的autodiff算法（由TensorFlow实现）只需要遍历两次图。作为对比，正向模式的autodiff算法需要为每个变量运行一次（如果我们需要10个不同变量的梯度，那么就需要执行10次）。对于符号微分，它会建立一个不同的图来计算梯度，所以根本不会遍历原来的图（除了在建立新的梯度图时）。一个高度优化的符号微分系统可能只需要运行一次新的梯度图来计算和所有变量相关的梯度，但与原始图相比，新的图可能时非常复杂和低效的。

10. 人工神经网络简介

  • 感知器

    • 《行为的组织》，1949，Donald Hebb：如果一个生物神经元总是出发另外的神经元，那么这两个神经元之间的连接就会变得更强。
    • Siegrid Lowel：同时处于激活状态的细胞时会连在一起的。
    • Hebb定律（又叫Hebbian学习）：当两个神经元有相同的输出时，它们之间的连接权重就会增强。
    • 感知器收敛定理（Rosenblatt）：如果训练实例是线性可分的，这个算法会收敛到一个解。

  • 线性阈值单元（LTU）

    import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron

iris = load_iris()
X = iris.data[:, (2, 3)]
y = (iris.target == 0).astype(np.int)
per_clf = Perceptron(random_state=42)
per_clf.fit(X, y)

y_pred = per_clf.predict([[2, 0.5]])
print(y_pred)

    • 事实上，在sklearn中，Perceptron类的行为等同于使用以下超参数的SGDClassifier：

      loss="perceptron", learning_rate="constant", eta0=1（学习速率）, penalty=None（不做正则化）

    • 注意和逻辑回归分类器相反，感知器不输出某个类的概率，它只能根据一个固定的阈值来做预测。这也是更应该使用逻辑回归而不是感知器的一个原因。

    • 感知器无法处理一些很微小的问题，比如异或分类问题（XOR），不过事实证明感知器的一些限制可以通过多层感知器来解决（Multi-Layer Perceptron，MLP）

  • 多层感知器和反向传播

    • 如果一个ANN有2个及以上的隐藏层，则被称为深度神经网络（DNN）。
    • 反向自动微分的梯度下降法：对于每个训练实例，反向传播算法先做一次预测（正向过程），度量误差，然后反向的遍历每个层次来度量每个连接的误差贡献度（反向过程），最后再微调每个连接的权重来降低误差（梯度下降）。

  • 使用TensorFlow的高级API来训练MLP

    • 用DNNClassifier类来训练一个有着任意数量隐藏层，并包含一个用来计算类别概率的sofmax输出层的神经网络。

      from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf

mnist = input_data.read_data_sets("D:/李添的数据哦！！！/BookStudy/book4/MNIST_data/MNIST_data/")

X_train = mnist.train.images
X_test = mnist.test.images
y_train = mnist.train.labels.astype("int")
y_test = mnist.test.labels.astype("int")

config = tf.contrib.learn.RunConfig(tf_random_seed=42) # not shown in the config

feature_cols = tf.contrib.learn.infer_real_valued_columns_from_input(X_train)
dnn_clf = tf.contrib.learn.DNNClassifier(hidden_units=[300,100], n_classes=10,
                                         feature_columns=feature_cols, config=config)
dnn_clf = tf.contrib.learn.SKCompat(dnn_clf) # if TensorFlow >= 1.1
dnn_clf.fit(X_train, y_train, batch_size=50, steps=40000)

    • 模型评估

      from sklearn.metrics import accuracy_score

y_pred = dnn_clf.predict(X_test)
accuracy_score(y_test, y_pred['classes'])

      from sklearn.metrics import log_loss

y_pred_proba = y_pred['probabilities']
log_loss(y_test, y_pred_proba)

    • 库还包含了一些方便的函数来评估模型：

      dnn_clf.score(X_test, y_test)

  • 使用纯TensorFlow训练DNN

    1. 构建阶段

      • 创建用于输入和目标值占位符节点

        import tensorflow as tf
import numpy as np

n_inputs = 28*28
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")

      • 创建用以创建神经网络的函数，使用它创建DNN

        • 手动

          def neuron_layer(X, n_neurons, name, activation=None):
    with tf.name_scope(name):
        n_inputs = int(X.get_shape()[1])
        stddev = 2 / np.sqrt(n_inputs)
        init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
        W = tf.Variable(init, name="weights")
        b = tf.Variable(tf.zeros([n_neurons]), name="biases")
        z = tf.matmul(X, W) + b
        if activation == "relu":
            return tf.nn.relu(z)
        else:
            return z

with tf.name_scope("dnn"):
    hidden1 = neuron_layer(X, n_hidden1, "hidden1", activation="relu")
    hidden2 = neuron_layer(hidden1, n_hidden2, "hidden2", activation="relu")
    logits = neuron_layer(hidden2, n_outputs, "outputs")

        • 利用fully_connected()函数来替换自己写的neuron_layer()函数

          from tensorflow.contrib.layers import fully_connected

with tf.name_scope("dnn"):
    hidden1 = fully_connected(X, n_hidden1, scope="hidden_1")
    hidden2 = fully_connected(hidden1, n_hidden2, scope="hidden_2")
    logits2 = fully_connected(hidden2, n_outputs, scope="outputs_", activation_fn=None)

      • 定义成本函数

        with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits2)
    loss = tf.reduce_mean(xentropy, name="loss")

      • 创建优化器

        learning_rate = 0.01
with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)

      • 定义性能度量

        with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits2, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

      • 最后初始化和保存模型

        init = tf.global_variables_initializer()
saver = tf.train.Saver()

      • tf.truncated_normal((n_inputs, n_neurons), stddev=np.sqrt(n_inputs))：使用标准偏差为2/sqrt(n_inputs)的阶段正态（高斯）分布进行随机初始化。使用截断的正态分布而不是常规的正态分布，保证这里不存在任何减慢训练的大权重。使用一个指定的标准偏差会让算法收敛得更快。

      • 为所有隐藏层随机地初始化连接权重值是非常重要的，这可以避免任何可能导致梯度下降出现无法终止的对称性。

      • tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)：它会根据“logits”来计算交叉熵（比如，在通过softmax激活函数之前网络的输出），并且期望以0到分类个数减1的整数形式标记。这会计算出一个包含每个实例的交叉熵的一维张量。可以用TensorFlow的reduce_mean()函数来计算所有实例的平均交叉熵。

      • 函数sparse_softmax_cross_entropy_with_logits()与先应用softmax函数再计算交叉熵的效果是一样的，不过它更高效一些，另外它会处理一些边界值如logits等于0的情况。这也是为什么我们之前没有使用softmax激活函数的原因。此外，还有一个softmax_cross_entropy_with_logits()函数，它以one-hot的形式获取标签（而不是从0到分类数量-1）

    2. 执行阶段

      from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("D:/李添的数据哦！！！/BookStudy/book4/MNIST_data/MNIST_data/")

n_epochs = 400
batch_size = 50

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for iteration in range(mnist.train.num_examples // batch_size):
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={
         X: X_batch, y: y_batch})
        acc_train = accuracy.eval(feed_dict={
         X: X_batch, y: y_batch})
        acc_test = accuracy.eval(feed_dict={
         X: mnist.test.images, y: mnist.test.labels})
        print(epoch, "Train accuracy：", acc_train, "Test accuracy：", acc_test)
    save_path = saver.save(sess, "D:/李添的数据哦！！！/BookStudy/book4/model/my_model_final.ckpt")
      • 先打开一个TensorFlow的对话。
      • 运行初始化代码来初始化所有的变量。
      • 运行主训练循环：在每一个周期（epoch）中，迭代一组和训练集大小相对应的批次，每一个小批次通过next_batch()方法来获得，然后执行训练操作，将当前小批次的输入数据和目标传入。
      • 接下来，在每个周期阶数的时候，代码会用上一个小批次以及全量的训练集来评估模型，并打印结果。
      • 最后，将模型的参数保存到硬盘。

    3. 使用神经网络

      • 保留构建期的代码，修改执行期的代码。
      with tf.Session() as sess:
    saver.restore(sess, "D:/李添的数据哦！！！/BookStudy/book4/model/my_model_final.ckpt")
    X_new_scaled = X_test[0].reshape(1, -1)
    Z = logits.eval(feed_dict={
         X: X_new_scaled})
    y_pred = np.argmax(Z, axis=1)
      • 首先从硬盘上加载模型参数。
      • 然后加载需要被分类的新图片。
      • 然后评估logits节点。
      • 如果你想知道所有分类的概率，你可以给logits使用softmax函数，如果你只是想预测一个分类，只需要选出那个有最大的logit值即可（argmax函数）。

  • 微调神经网络的超参数

    • 利用随机搜索法
    • 使用像Oscar这样的工具

    1. 隐藏层的个数

      • 深层网络比浅层网络有更高的参数效率：深层网络可以用非常少的神经元来建模复杂函数，因此训练起来更加快速。
      • 现实世界的数据往往会按照层次结构组织，而DNN天生的就很擅长处理这种数据：低级隐藏层用以建模低层结构，中级隐藏层组合这些低层结构来建模中层结构，高级隐藏层和输出层组合这些中层结构来构建高层结构。
      • 分层的架构不仅可以帮助DNN更快的归纳出好方案，还可以提高对于新数据集的泛化能力。

    • 每个隐藏层中的神经元数

      • 输入输出层中的神经元数由任务要求的输入输出类型决定。
      • 对于隐藏层来说，一个常用的实践是以漏斗型来定义其尺寸，每层的神经元数依次减少：原因是许多低级功能可以合并成数量更少的高级功能。
      • 不过，这种实践现在也不那么常用了，你可以将所有层次定义为同一尺寸，每个隐藏层各150个神经元：这只是一个超参数调整。
      • 一个更简单的做法是使用（比实际所需）更多的层次和神经元，然后提前结束训练来避免过度拟合（以及其他的正则化技术，特别是dropout）。这被称为弹力裤方法。无须花费时间找刚好适合你的裤子，随便挑弹力裤，它会缩小到合适的尺寸。

    • 激活函数

      • 大多数情况下，你可以在隐藏层中使用ReLU激活函数（或者其变种），它比其他激活函数要快一些，因为梯度下降对于大输入值没有上限，会导致它无法终止（与逻辑函数或者双曲正切函数刚好相反，它们会在1处饱和）。
      • 对于输出层，softmax激活函数对于分类任务（如果分类是互斥的）来说是一个很不错的选择。对于回归任务，则完全可以不使用激活函数。

  • 练习摘抄

    • 为什么通常更倾向用逻辑回归分类器而不是经典的感知器？如何调整一个感知器，让它与逻辑回归分类器等价？

      经典的感知器只有在数据集是线性可分的情况下才会收敛，并且不能估计分类的概率。作为对比，逻辑回归分类器即使在数据集不是线性可分的情况下也可以很好的收敛，而且还能输出分类的概率。

      如果你将感知器的激活函数修改为逻辑激活函数（或者如果有多个神经元的时候，采用softmax激活函数），然后训练其使用梯度下降（或者使成本函数最小化的一些其他优化算法，通常使交叉熵法），那么它就会变成一个逻辑回归分类器了。

    • 为什么逻辑激活函数是训练第一个MLP的关键因素？

      因为它的导数总是非零的，所以梯度下降总是可以持续的。当激活功能是一个阶梯函数时，渐变下降就不能再持续了，因为这时候根本没有斜率。

    • 什么时反向传播，它时如何工作的？反向传播与反式自动微分有何区别？

      反向传播是一种用于训练人工神经网络的技术。它首先计算关于每个模型参数（所有的权重和偏差）的成本函数的梯度，然后使用这些梯度执行梯度下降。这种反向传播步骤通常执行数千次或数百万次，并需要多个训练批次，直到模型参数收敛到最小化成本函数的值为止。为了计算梯度，反向传播使用反向模式autodiff（尽管在反向传播被发明的时候还不叫autodiff，事实上autodiff的概念已经被重新发明了多次）。

      反向模式的autodiff会先在计算图上正向执行一次，计算按当前训练批次的每个节点的值，然后反向执行一次，一次性计算所有梯度。

      那和反向传播有什么区别呢？反向传播是指使用多个反向传播步骤来训练人工神经网络的全部过程，每个步骤计算梯度并使用它们执行梯度下降的过程。相反，反向模式autodiff只是一种简单的计算梯度的技术，只是恰好被反向传播使用了而已。

11. 训练深度神经网络

  • 梯度消失/爆炸问题

    • 梯度消失：梯度经常会随着算法进展到更低层时变得越来越小。导致的结果是，梯度下降在更低层网络连接权值更新方面基本没有改变，而且训练不会收敛到好的结果。
    • 梯度爆炸：在一些例子中会发生相反的现象，梯度越来越大，导致很多层的权值疯狂增大，使得算法发散。（经常出现在循环神经网络中）。
    • 简单来讲，深度神经网络受制于不稳定梯度，不同层可能会以完全不同的速度学习。

  • Xavier初始化和He初始化

    • 在Glorot和Bengio的论文中提出，当预测的时候要保持正向，在反向传播梯度的时保持反方向。为了让信号正确流动，作者提出需要保持每一层的输入和输出的方差一致，并且需要在反向流动过某一层时，前后的方差也要一致。事实上，这是很难保证的，除非一层有相同数量的输入和输出连接。因此它们提出了一个很好的这种方案：

    • 连接的权重必须按照以下公式进行随机初始化，其中 n i n p u t s n_{inputs} ninputs​和 n o u t p u t s n_{outputs} noutputs​是权重被初始化层的输入和输出连接数（也称为扇入和扇出）。这种初始化方法称为Xavier初始化（当使用逻辑激活函数时）。同理，ReLU激活函数的初始化方法及其变种称为He初始化。

      激活函数 均匀分布-r、r 正态分布
      逻辑函数 r = 6 n i n p u t s + n o u t p u t s r=\sqrt{ \frac{6}{n_{inputs} + n_{outputs}} } r=ninputs​+noutputs​6​ ​ σ = 2 n i n p u t s + n o u t p u t s \sigma=\sqrt{ \frac{2}{n_{inputs} + n_{outputs}} } σ=ninputs​+noutputs​2​ ​
      双曲正切函数 r = 6 n i n p u t s + n o u t p u t s 4 r=\sqrt[4]{ \frac{6}{n_{inputs} + n_{outputs}} } r=4ninputs​+noutputs​6​ ​ σ = 2 n i n p u t s + n o u t p u t s 4 \sigma=\sqrt[4]{ \frac{2}{n_{inputs} + n_{outputs}} } σ=4ninputs​+noutputs​2​ ​
      ReLU（及变种） r = 6 n i n p u t s + n o u t p u t s 2 r=\sqrt[\sqrt2]{ \frac{6}{n_{inputs} + n_{outputs}} } r=2 ​ninputs​+noutputs​6​ ​ σ = 2 n i n p u t s + n o u t p u t s 2 \sigma=\sqrt[\sqrt2]{ \frac{2}{n_{inputs} + n_{outputs}} } σ=2 ​ninputs​+noutputs​2​ ​

  • 非饱和激活函数

    • ReLU函数并不是完美的。它会出现dying ReLU问题：在训练过程中，一些神经元实际上已经死了，即它们只输出0。在训练过程中，如果神经元的权重更新到神经元输入的总权重是负值时，这个神经元就会开始输出0。当这种情况发生时，除非ReLU函数的梯度为0并且输入为负，否则这个神经元就不会再重新开始工作。

    • 要解决这个问题，可以使用ReLU函数的变种，比如leaky ReLU（带泄露线性整流函数）。这个函数定义为 L e a k y R e L U a ( z ) = m a x ( a z , z ) LeakyReLU_a(z)=max(az, z) LeakyReLUa​(z)=max(az,z)。超参数a表示函数“泄露”程度：它是函数中z<0时的坡度，这个小坡度可以保证leaky ReLU不会死，它可以进入一个很长的昏迷其，但最后还是有机会醒过来。

    • 最后，Clevert等人提出了一个新的激活函数，称为ELU（加速线性单元），它的表现优于ReLU的所有变种：训练时间减小，神经网络再测试集的表现也更好。

      E L U a ( z ) = { a ( e x p ( z ) − 1 ) z < 0 z z ≥ 0 ELU_a(z)= \begin{cases} a(exp(z)-1) & z<0 \\ z & z \geq 0 \end{cases} ELUa​(z)={ a(exp(z)−1)z​z<0z≥0​

      • 当 z ≤ 0 z \leq 0 z≤0时它的值为负，从而允许单元的平均输出接近0。这样就可以缓和梯度消失的问题。超参数a是指当z是一个极大的负数时，ELU函数接近的那个值。
      • 对于z<0有一个非零的梯度，这样就可以避免单元消失的问题。
      • 这个函数整体很平滑，包括在z=0附近，这样就可以提高梯度下降，因为在z=0的左右两边都没有抖动。
      • ELU激活函数的一个主要缺陷是计算速度比ReLU和它的变种慢（因为使用了指数函数），但是在训练过程中，可以通过更快的收敛速度来弥补。然而，测试中，ELU网络时间慢于ReLU网络。

    • 那么在你的深度神经网络的隐藏层到底应该使用哪一种激活函数呢？

      • 通常来说ELU函数>leaky ReLU函数（和它的变种）>ReLU函数>tanh函数>逻辑函数。
      • 如果你更关心运行时的性能，那你可以选择leaky ReLU函数，而不是ELU函数。
      • 如果你不想改变别的超参数，就只使用建议a的默认值（leaky ReLU函数是0.01，ELU函数是1）。
      • 如果你有多余的时间和计算能力，可以使用交叉验证去评估别的激活函数
      • 如果你的网络过拟合，可以使用RReLU函数
      • 如果针对大的训练集，可以使用PReLU函数。

    • 使用elu激活函数：hidden1 = fully_connected(X, n_hidden1, activation_fn=tf.nn.elu)

    • 使用leaky ReLU激活函数：

      def leaky_relu(z, name=None):
	return tf.maximum(0.01 * z, z, name=name)
hidden1 = fully_connected(X, n_hidden1, activation_fn=leaky_relu)

  • 批量归一化

    • 尽管使用了He初始化加ELU可以很明显地在训练初期降低梯度消失/爆炸问题，但还是不能保证在训练过程中不会再出现这些问题。
    • 用来解决梯度消失/爆炸的问题，而且每一层的输入分散问题再训练过程中更普遍，前层变量的改变（称为内部协变量转变问题）也是一样。
    • 该技术包括在每一层激活函数之前在模型里加一个操作，简单零中心化和归一化输入，之后再通过每层的两个新参数（一个为了缩放，一个为了移动）缩放和移动结果。换句话说，这个操作让模型学会了最佳规模和每层输入的平均值。
    • 整体看来，4个参数是为每一批量归一化层来学习的： γ \gamma γ（缩放）， β \beta β（偏移）， μ \mu μ（平均值）和 σ \sigma σ（标准方差）。
    • 批量归一化同时还可以进行正则化，降低其他正则化技术的需求。
    • 你会发现一开始当梯度下降再每一层搜索最佳缩放和偏移量时，训练速度会非常慢，但是一旦找到一个合适的值，训练速度就会迅速提升。

  • 无监督的预训练

    • 场景：完成一个没有太多标记训练数据的复杂任务，并且没有找到在近似任务上训练过的模型。
    • 方法：逐层训练它们，从最低层开始，然后向上，利用一种 非监督特性检测算法 ，比如 受限玻尔兹曼机（RBM） 或者 自动编码器 。
    • 另一种方法是：针对你可以很方便找到大量标记的训练数据运行一个监督任务，然后使用 迁移学习 。比如，你想要训练一个模型来识别出图片里的朋友，你可以在网上下载成千上万张脸，然后训练一个分类器来检测两张脸是否一致，之后用这个个分类器来对比新图片和每一张你朋友的图片。

  • 辅助任务中的预训练

    • 场景：构建一个人脸识别系统，但是你的样本很少。

    • 方法：在网上收集很多随机的人像图片，用他们可以训练第一个神经网络来检测两张不同的照片是否是同一个人，从而得到一个人脸特征检测器，然后重用这个网络的低层，这样就能用很少的训练数据训练出一个优质的人脸分类器。

      标记
      方法1
      标记为好
      标记为不好
      方法2
      较高的好的实例得分
      较低的坏的实例得分

  • 快速优化器

    • 四种提高训练速度的方法
      1. 在连接权重上应用一个良好的初始化策略
      2. 使用一个良好的激活函数
      3. 使用批量归一化
      4. 重用部分预处理网络
    • 常用的快速优化器
      1. Momentum（动量优化）
      2. NAG（Nesterov梯度加速）
      3. AdaGrad
      4. RMSProp
      5. Adam优化

  • 学习速率调度

    • 以一个高学习速率开始，然后一旦它停止快速过程就降低速率，那么你会获得一个比最优固定学习速率梗快速的方案。

    • 常用学习计划：

      • 预定分段常数学习速率

      • 性能调度

      • 指数调度：

        推荐，因为更容易实现、微调，且收敛到最优解的速度稍快

      • 功率调度

  • 通过正则化避免过度拟合

    • TensorFlow中常用的正则化技术有：
      1. 提前停止
      2. l 1 l1 l1和 l 2 l2 l2正则化
      3. dropout
      4. 最大范数正则化
      5. 数据扩充

12. 跨设备和服务器的分布式TensorFlow

  • 数据出队
    • 顺序执行dequeue或dequeue_many操作，只要队列里有数据就会一直成功，但当队列中元素不足时就会失败。
    • dequeue_many会丢弃队列中个数小于批量值的数据
    • dequeue_up_to会保留
  • 队列类型：
    • FIFOQueue：先进先出队列
    • RandomShuffleQueue：全数据集随机队列
    • PaddingFifoQueue：出队时，用零填充所有维度，保持和最大维度一致
  • 在TensorFLow集群上并行化神经网络
    • 图内复制与图间复制
    • 模型并行化与数据并行化
    • 同步更新和异步更新

13. 卷积神经网络

  • 利用过滤器绘制特征图

    import numpy as np
from sklearn.datasets import load_sample_images
import tensorflow as tf
import matplotlib.pyplot as plt

dataset = np.array(load_sample_images().images, dtype=np.float32)
batch_size, height, width, channels = dataset.shape

filters_test = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filters_test[:, 3, :, 0] = 1
filters_test[3, :, :, 1] = 1

X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
convolution = tf.nn.conv2d(X, filters_test, strides=[1, 2, 2, 1], padding="SAME")

with tf.Session() as sess:
    output = sess.run(convolution, feed_dict={
       X: dataset})
    plt.imshow(output[0, :, :, 1])
    plt.show()

    输出结果

    《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第3张图片

  • 常用的卷积神经网络

    • LeNet-5
    • AlexNet
    • GoogLeNet
    • ResNet
    • CGGNet
    • Inception-v4

14. 循环神经网络

  • TensorFlow中的基本RNN

    • 假设RNN只运行两个时间迭代，每个时间迭代输入一个大小为3的向量。

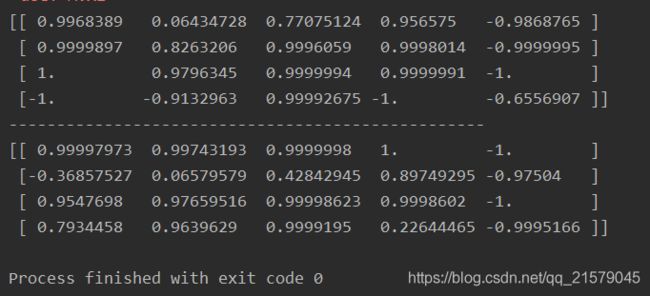
      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
    @author: Li Tian
    @contact: [email protected]
    @software: pycharm
    @file: simple_rnn.py
    @time: 2019/6/15 16:53
    @desc: 实现一个最简单的RNN网络。我们将使用tanh激活函数创建一个由5个
            神经元组成的一层RNN。假设RNN只运行两个时间迭代，每个时间迭代
            输入一个大小为3的向量。
    """
import tensorflow as tf
import numpy as np

n_inputs = 3
n_neurons = 5

x0 = tf.placeholder(tf.float32, [None, n_inputs])
x1 = tf.placeholder(tf.float32, [None, n_inputs])

Wx = tf.Variable(tf.random_normal(shape=[n_inputs, n_neurons], dtype=tf.float32))
Wy = tf.Variable(tf.random_normal(shape=[n_neurons, n_neurons], dtype=tf.float32))
b = tf.Variable(tf.zeros([1, n_neurons], dtype=tf.float32))

y0 = tf.tanh(tf.matmul(x0, Wx) + b)
y1 = tf.tanh(tf.matmul(y0, Wy) + tf.matmul(x1, Wx) + b)

init = tf.global_variables_initializer()

# Mini-batch：包含4个实例的小批次
x0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]])   # t=0
x1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]])   # t=1

with tf.Session() as sess:
    init.run()
    y0_val, y1_val = sess.run([y0, y1], feed_dict={
         x0: x0_batch, x1: x1_batch})
    print(y0_val)
    print('-'*50)
    print(y1_val)

    • 运行结果

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第4张图片

  • 通过时间静态展开

    • static_rnn()函数通过链式单元来创建一个展开的RNN网络。

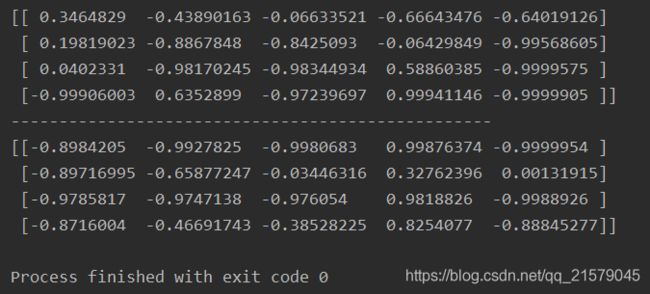
      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: simple_rnn2.py
@time: 2019/6/15 17:06
@desc: 与前一个程序相同
"""

import tensorflow as tf
from tensorflow.contrib.rnn import BasicRNNCell
from tensorflow.contrib.rnn import static_rnn
import numpy as np

n_inputs = 3
n_neurons = 5

x0 = tf.placeholder(tf.float32, [None, n_inputs])
x1 = tf.placeholder(tf.float32, [None, n_inputs])

basic_cell = BasicRNNCell(num_units=n_neurons)
output_seqs, states = static_rnn(basic_cell, [x0, x1], dtype=tf.float32)

y0, y1 = output_seqs

init = tf.global_variables_initializer()

# Mini-batch：包含4个实例的小批次
x0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]])   # t=0
x1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]])   # t=1

with tf.Session() as sess:
    init.run()
    y0_val, y1_val = sess.run([y0, y1], feed_dict={
         x0: x0_batch, x1: x1_batch})
    print(y0_val)
    print('-'*50)
    print(y1_val)

    • 运行结果

    《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第5张图片

  • 通过时间动态展开

    • 利用dynamic_rnn()和while_loop()

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: dynamic_rnn1.py
@time: 2019/6/16 13:37
@desc:  通过时间动态展开 dynamic_rnn
"""

import tensorflow as tf
from tensorflow.contrib.rnn import BasicRNNCell
import numpy as np


n_steps = 2
n_inputs = 3
n_neurons = 5

x = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
basic_cell = BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, x, dtype=tf.float32)

x_batch = np.array([
    [[0, 1, 2], [9, 8, 7]],
    [[3, 4, 5], [0, 0, 0]],
    [[6, 7, 8], [6, 5, 4]],
    [[9, 0, 1], [3, 2, 1]],
])

init = tf.global_variables_initializer()

with tf.Session() as sess:
    init.run()
    outputs_val = outputs.eval(feed_dict={
         x: x_batch})
    print(outputs_val)

    • 运行结果

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第6张图片

      这时问题来了，动态、静态这两种有啥区别呢？

      参考：tensor flow dynamic_rnn 与rnn有啥区别？

  • 处理长度可变输入序列

    #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: dynamic_rnn2.py
@time: 2019/6/17 9:42
@desc: 处理长度可变输入序列
"""

import tensorflow as tf
from tensorflow.contrib.rnn import BasicRNNCell
import numpy as np


n_steps = 2
n_inputs = 3
n_neurons = 5

seq_length = tf.placeholder(tf.int32, [None])
x = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
basic_cell = BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, x, dtype=tf.float32, sequence_length=seq_length)

# 假设第二个输出序列仅包含一个输入。为了适应输入张量X，必须使用零向量填充输入。
x_batch = np.array([
    [[0, 1, 2], [9, 8, 7]],
    [[3, 4, 5], [0, 0, 0]],
    [[6, 7, 8], [6, 5, 4]],
    [[9, 0, 1], [3, 2, 1]],
])

seq_length_batch = np.array([2, 1, 2, 2])

init = tf.global_variables_initializer()

with tf.Session() as sess:
    init.run()
    outputs_val, states_val = sess.run([outputs, states], feed_dict={
       x: x_batch, seq_length: seq_length_batch})
    print(outputs_val)
    • 运行结果

    《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第7张图片

    • 结果分析

      RNN每一次迭代超过输入长度的部分输出零向量。

      此外，状态张量包含了每个单元的最终状态（除了零向量）。

  • 处理长度可变输出序列

  • 最通常的解决方案是定义一种被称为**序列结束令牌（EOS token）**的特殊输出。

  • 训练RNN

  • 通过时间反向传播（BPTT）：梯度通过被成本函数使用的所有输出向后流动，而不是仅仅通过输出最终输出。

  • 训练序列分类器

    #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: rnn_test1.py
@time: 2019/6/17 10:28
@desc: 训练一个识别MNIST图像的RNN网络。
"""

import tensorflow as tf
from tensorflow.contrib.layers import fully_connected
from tensorflow.contrib.rnn import BasicRNNCell

from tensorflow.examples.tutorials.mnist import input_data


n_steps = 28
n_inputs = 28
n_neurons = 150
n_outputs = 10

learning_rate = 0.001

n_epochs = 100
batch_size = 150

X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.int32, [None])

basic_cell = BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)

logits = fully_connected(states, n_outputs, activation_fn=None)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)

loss = tf.reduce_mean(xentropy)
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()

# 加载MNIST数据，并按照网格的要求改造测试数据。
mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')
X_test = mnist.test.images.reshape((-1, n_steps, n_inputs))
y_test = mnist.test.labels

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for iteration in range(mnist.train.num_examples // batch_size):
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            X_batch = X_batch.reshape((-1, n_steps, n_inputs))
            sess.run(training_op, feed_dict={
       X: X_batch, y: y_batch})

        acc_train = accuracy.eval(feed_dict={
       X: X_batch, y: y_batch})
        acc_test = accuracy.eval(feed_dict={
       X: X_test, y: y_test})
        print(epoch, "Train accuracy: ", acc_train, "Test accuracy: ", acc_test)

    • 运行结果

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第8张图片

      tf.nn.in_top_k：主要是用于计算预测的结果和实际结果的是否相等，返回一个bool类型的张量，tf.nn.in_top_k(prediction, target, K):prediction就是表示你预测的结果，大小就是预测样本的数量乘以输出的维度，类型是tf.float32等。target就是实际样本类别的索引，大小就是样本数量的个数。K表示每个样本的预测结果的前K个最大的数里面是否含有target中的值。一般都是取1。

      参考链接：tf.nn.in_top_k的用法

      tf.cast：将x的数据格式转化成dtype。例如，原来x的数据格式是bool，那么将其转化成float以后，就能够将其转化成0和1的序列。反之也可以。

      cast(
    x,
    dtype,
    name=None
)

  • 训练预测时间序列

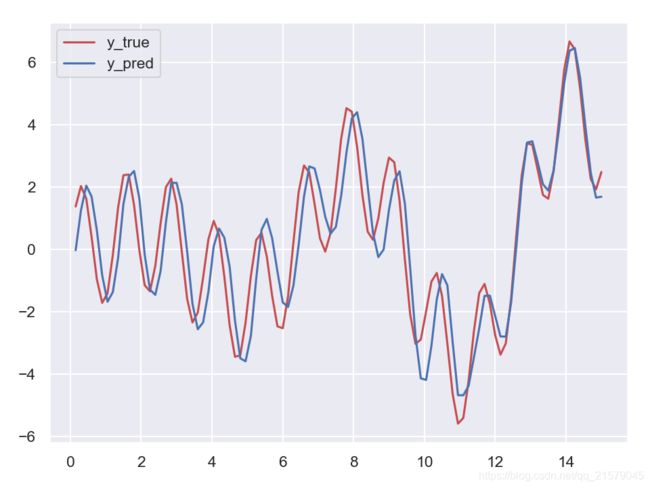
    #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: rnn_test2.py
@time: 2019/6/18 10:11
@desc: 训练预测时间序列
"""

import tensorflow as tf
import numpy as np
from tensorflow.contrib.layers import fully_connected
from tensorflow.contrib.rnn import BasicRNNCell
from tensorflow.contrib.rnn import OutputProjectionWrapper
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()


n_steps = 100
n_inputs = 1
n_neurous = 100
n_outputs = 1

learning_rate = 0.001

n_iterations = 10000
batch_size = 50

X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])

# 现在在每个时间迭代，有一个大小为100的输出向量，但是实际上我们需要一个单独的输出值。
# 最简单的解决方案是将单元格包装在OutputProjectionWrapper中。
# cell = OutputProjectionWrapper(BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu), output_size=n_outputs)

# 用技巧提高速度
cell = BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu)
rnn_outputs, states = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurous])
stacked_outputs = fully_connected(stacked_rnn_outputs, n_outputs, activation_fn=None)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])

loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

X_data = np.linspace(0, 15, 101)
with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        X_batch = X_data[:-1][np.newaxis, :, np.newaxis]
        y_batch = X_batch * np.sin(X_batch) / 3 + 2 * np.sin(5 * X_batch)
        sess.run(training_op, feed_dict={
       X: X_batch, y: y_batch})
        if iteration % 100 == 0:
            mse = loss.eval(feed_dict={
       X: X_batch, y: y_batch})
            print(iteration, "\tMSE", mse)

    X_new = X_data[1:][np.newaxis, :, np.newaxis]
    y_true = X_new * np.sin(X_new) / 3 + 2 * np.sin(5 * X_new)
    y_pred = sess.run(outputs, feed_dict={
       X: X_new})

print(X_new.flatten())
print('真实结果：', y_true.flatten())
print('预测结果：', y_pred.flatten())

fig = plt.figure(dpi=150)
plt.plot(X_new.flatten(), y_true.flatten(), 'r', label='y_true')
plt.plot(X_new.flatten(), y_pred.flatten(), 'b', label='y_pred')
plt.legend()
plt.show()

    • 运行结果

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第9张图片

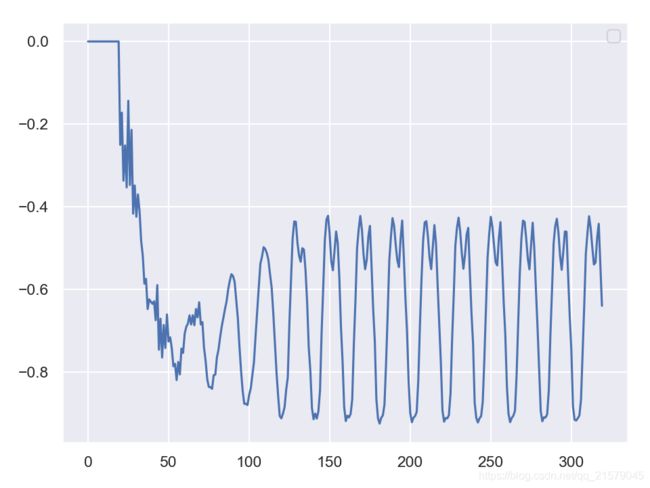
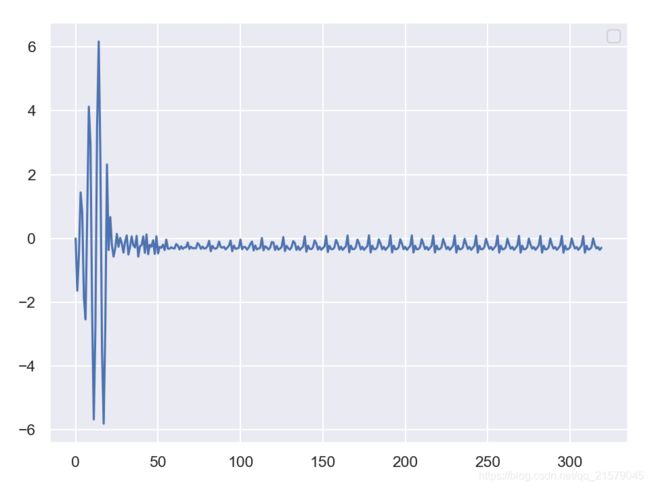
  • 创造性的RNN

    #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: rnn_test3.py
@time: 2019/6/19 8:47
@desc: 创造性RNN
"""

import tensorflow as tf
import numpy as np
from tensorflow.contrib.layers import fully_connected
from tensorflow.contrib.rnn import BasicRNNCell
from tensorflow.contrib.rnn import OutputProjectionWrapper
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()


n_steps = 20
n_inputs = 1
n_neurous = 100
n_outputs = 1

learning_rate = 0.001

n_iterations = 10000
batch_size = 50

X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])

# 现在在每个时间迭代，有一个大小为100的输出向量，但是实际上我们需要一个单独的输出值。
# 最简单的解决方案是将单元格包装在OutputProjectionWrapper中。
# cell = OutputProjectionWrapper(BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu), output_size=n_outputs)

# 用技巧提高速度
cell = BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu)
rnn_outputs, states = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurous])
stacked_outputs = fully_connected(stacked_rnn_outputs, n_outputs, activation_fn=None)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])

loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

X_data = np.linspace(0, 19, 20)
with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        X_batch = X_data[np.newaxis, :, np.newaxis]
        y_batch = X_batch * np.sin(X_batch) / 3 + 2 * np.sin(5 * X_batch)
        sess.run(training_op, feed_dict={
       X: X_batch, y: y_batch})
        if iteration % 100 == 0:
            mse = loss.eval(feed_dict={
       X: X_batch, y: y_batch})
            print(iteration, "\tMSE", mse)

    # sequence = [0.] * n_steps
    sequence = list(y_batch.flatten())
    for iteration in range(300):
        XX_batch = np.array(sequence[-n_steps:]).reshape(1, n_steps, 1)
        y_pred = sess.run(outputs, feed_dict={
       X: XX_batch})
        sequence.append(y_pred[0, -1, 0])

fig = plt.figure(dpi=150)
plt.plot(sequence)
plt.legend()
plt.show()

    • 结果1：使用零值作为种子序列

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第10张图片

    • 结果2：使用实例作为种子序列

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第11张图片

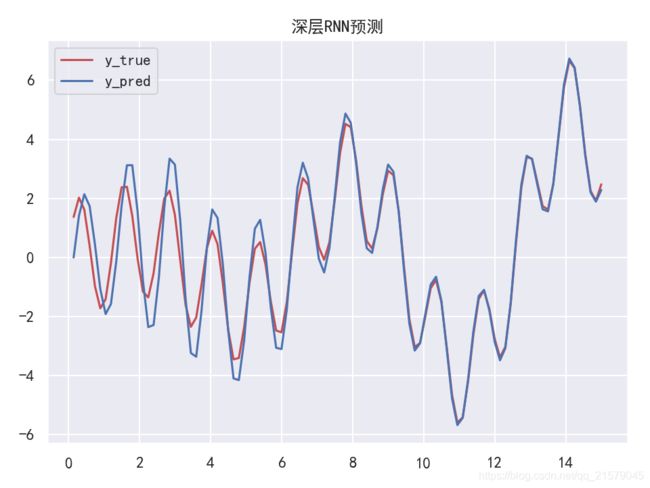
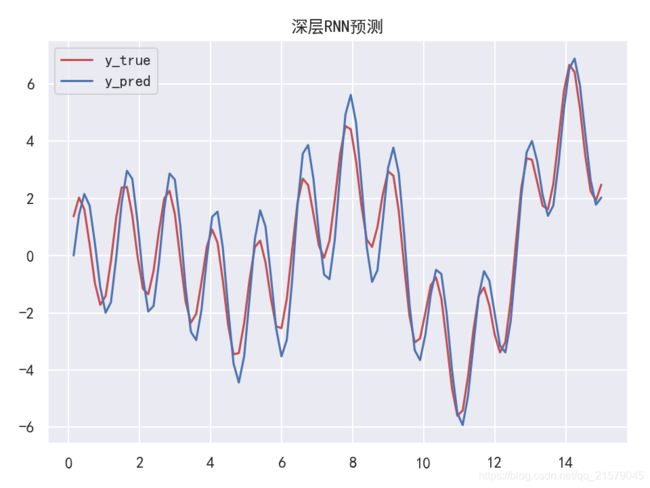
  • 深层RNN

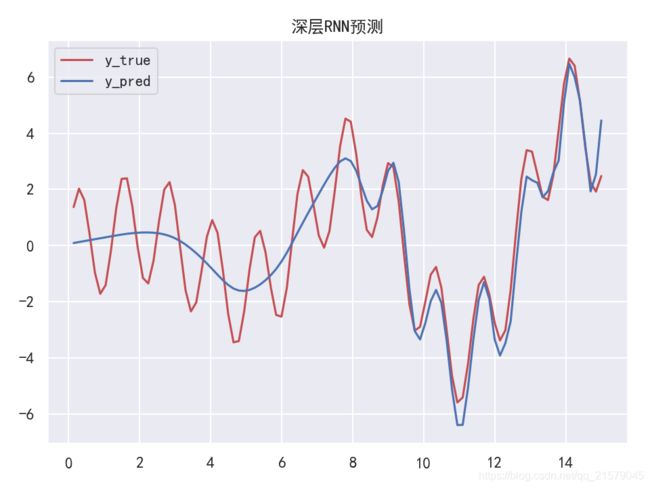
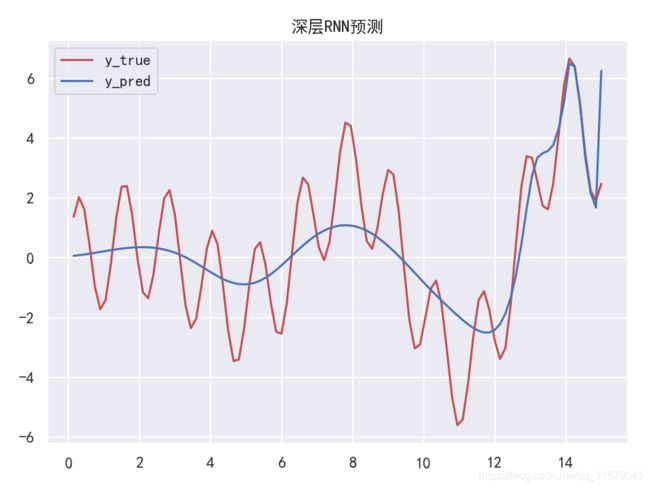
    #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: rnn_test4.py
@time: 2019/6/19 10:10
@desc: 深层RNN
"""

import tensorflow as tf
import numpy as np
from tensorflow.contrib.layers import fully_connected
from tensorflow.contrib.rnn import BasicRNNCell
from tensorflow.contrib.rnn import MultiRNNCell
from tensorflow.contrib.rnn import OutputProjectionWrapper
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()


n_steps = 100
n_inputs = 1
n_neurous = 100
n_outputs = 1

n_layers = 10

learning_rate = 0.00001

n_iterations = 10000
batch_size = 50

X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])

# 现在在每个时间迭代，有一个大小为100的输出向量，但是实际上我们需要一个单独的输出值。
# 最简单的解决方案是将单元格包装在OutputProjectionWrapper中。
# cell = OutputProjectionWrapper(BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu), output_size=n_outputs)

# 用技巧提高速度
# cell = BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu)
# multi_layer_cell = MultiRNNCell([cell] * n_layers)
layers = [BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu) for _ in range(n_layers)]
multi_layer_cell = MultiRNNCell(layers)
rnn_outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurous])
stacked_outputs = fully_connected(stacked_rnn_outputs, n_outputs, activation_fn=None)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])

loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

X_data = np.linspace(0, 15, 101)
with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        X_batch = X_data[:-1][np.newaxis, :, np.newaxis]
        y_batch = X_batch * np.sin(X_batch) / 3 + 2 * np.sin(5 * X_batch)
        sess.run(training_op, feed_dict={
       X: X_batch, y: y_batch})
        if iteration % 100 == 0:
            mse = loss.eval(feed_dict={
       X: X_batch, y: y_batch})
            print(iteration, "\tMSE", mse)

    X_new = X_data[1:][np.newaxis, :, np.newaxis]
    y_true = X_new * np.sin(X_new) / 3 + 2 * np.sin(5 * X_new)
    y_pred = sess.run(outputs, feed_dict={
       X: X_new})

print(X_new.flatten())
print('真实结果：', y_true.flatten())
print('预测结果：', y_pred.flatten())

plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig = plt.figure(dpi=150)
plt.plot(X_new.flatten(), y_true.flatten(), 'r', label='y_true')
plt.plot(X_new.flatten(), y_pred.flatten(), 'b', label='y_pred')
plt.title('深层RNN预测')
plt.legend()
plt.show()

    • 运行结果

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第12张图片

  • 在多个GPU中分配一个深层RNN

    • 并没有多个GPU，所以只是整理了一下代码。。。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: rnn_gpu.py
@time: 2019/6/19 12:11
@desc: 在多个GPU中分配一个深层RNN
"""

import tensorflow as tf
import numpy as np
from tensorflow.contrib.rnn import RNNCell
from tensorflow.contrib.rnn import BasicRNNCell
from tensorflow.contrib.rnn import MultiRNNCell
from tensorflow.contrib.layers import fully_connected

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()


class DeviceCellWrapper(RNNCell):
    def __init__(self, device, cell):
        self._cell = cell
        self._device = device

    @property
    def state_size(self):
        return self._cell.state_size

    @property
    def output(self):
        return self._cell.output_size

    def __call__(self, inputs, state, scope=None):
        with tf.device(self._device):
            return self._cell(inputs, state, scope)


n_steps = 100
n_inputs = 1
n_neurous = 100
n_outputs = 1

n_layers = 10

learning_rate = 0.00001

n_iterations = 10000
batch_size = 50

X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])


devices = ['/gpu:0', '/gpu:1', '/gpu:2']
cells = [DeviceCellWrapper(dev, BasicRNNCell(num_units=n_neurous)) for dev in devices]
multi_layer_cell = MultiRNNCell(cells)
rnn_outputs,  states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)

stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurous])
stacked_outputs = fully_connected(stacked_rnn_outputs, n_outputs, activation_fn=None)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])

loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

X_data = np.linspace(0, 15, 101)
with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        X_batch = X_data[:-1][np.newaxis, :, np.newaxis]
        y_batch = X_batch * np.sin(X_batch) / 3 + 2 * np.sin(5 * X_batch)
        sess.run(training_op, feed_dict={
         X: X_batch, y: y_batch})
        if iteration % 100 == 0:
            mse = loss.eval(feed_dict={
         X: X_batch, y: y_batch})
            print(iteration, "\tMSE", mse)

    X_new = X_data[1:][np.newaxis, :, np.newaxis]
    y_true = X_new * np.sin(X_new) / 3 + 2 * np.sin(5 * X_new)
    y_pred = sess.run(outputs, feed_dict={
         X: X_new})

print(X_new.flatten())
print('真实结果：', y_true.flatten())
print('预测结果：', y_pred.flatten())

plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig = plt.figure(dpi=150)
plt.plot(X_new.flatten(), y_true.flatten(), 'r', label='y_true')
plt.plot(X_new.flatten(), y_pred.flatten(), 'b', label='y_pred')
plt.title('深层RNN预测')
plt.legend()
plt.show()

  • 应用丢弃机制

    #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: rnn_test5.py
@time: 2019/6/19 13:44
@desc: 应用丢弃机制
"""


import tensorflow as tf
import sys
import numpy as np
from tensorflow.contrib.layers import fully_connected
from tensorflow.contrib.rnn import BasicRNNCell
from tensorflow.contrib.rnn import MultiRNNCell
from tensorflow.contrib.rnn import OutputProjectionWrapper
from tensorflow.contrib.rnn import DropoutWrapper
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()


is_training = (sys.argv[-1] == "train")
keep_prob = 0.5
n_steps = 100
n_inputs = 1
n_neurous = 100
n_outputs = 1

n_layers = 10

learning_rate = 0.00001

n_iterations = 10000
batch_size = 50


def make_rnn_cell():
    return BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu)


def make_drop_cell():
    return DropoutWrapper(make_rnn_cell(), input_keep_prob=keep_prob)


X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])

# 现在在每个时间迭代，有一个大小为100的输出向量，但是实际上我们需要一个单独的输出值。
# 最简单的解决方案是将单元格包装在OutputProjectionWrapper中。
# cell = OutputProjectionWrapper(BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu), output_size=n_outputs)

# 用技巧提高速度
layers = [make_rnn_cell() for _ in range(n_layers)]
if is_training:
    layers = [make_drop_cell() for _ in range(n_layers)]

multi_layer_cell = MultiRNNCell(layers)
rnn_outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurous])
stacked_outputs = fully_connected(stacked_rnn_outputs, n_outputs, activation_fn=None)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])

loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

X_data = np.linspace(0, 15, 101)

'''
# 应用丢弃机制
saver = tf.train.Saver()

with tf.Session() as sess:
    if is_training:
        init.run()
        for iteration in range(n_iterations):
            # train the model
        save_path = saver.save(sess, "./my_model.ckpt")
    else:
        saver.restore(sess, "./my_model.ckpt")
        # use the model
'''

with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        X_batch = X_data[:-1][np.newaxis, :, np.newaxis]
        y_batch = X_batch * np.sin(X_batch) / 3 + 2 * np.sin(5 * X_batch)
        sess.run(training_op, feed_dict={
       X: X_batch, y: y_batch})
        if iteration % 100 == 0:
            mse = loss.eval(feed_dict={
       X: X_batch, y: y_batch})
            print(iteration, "\tMSE", mse)

    X_new = X_data[1:][np.newaxis, :, np.newaxis]
    y_true = X_new * np.sin(X_new) / 3 + 2 * np.sin(5 * X_new)
    y_pred = sess.run(outputs, feed_dict={
       X: X_new})

print(X_new.flatten())
print('真实结果：', y_true.flatten())
print('预测结果：', y_pred.flatten())

plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig = plt.figure(dpi=150)
plt.plot(X_new.flatten(), y_true.flatten(), 'r', label='y_true')
plt.plot(X_new.flatten(), y_pred.flatten(), 'b', label='y_pred')
plt.title('深层RNN预测')
plt.legend()
plt.show()

    • 运行结果

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第13张图片

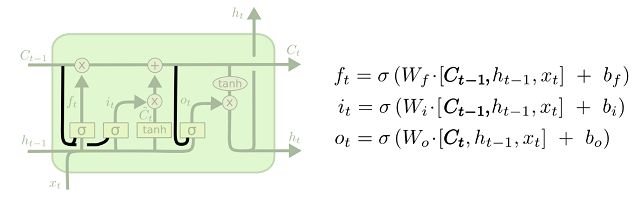
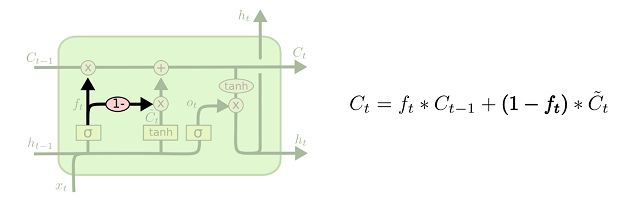
  • LSTM单元

    • 四个不同的全连接层：主层：tanh，直接输出 y t 和 h t y_t和h_t yt​和ht​；忘记门限：logitstic，控制着哪些长期状态应该被丢弃；输入门限：控制着主层的哪些部分会被加入到长期状态（这就是“部分存储”的原因）；输出门限：控制着哪些长期状态应该在这个时间迭代被读取和输出（ h t 和 y t h_t和y_t ht​和yt​）。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: lstm_test1.py
@time: 2019/6/19 14:51
@desc: LSTM单元
"""

import tensorflow as tf
import sys
import numpy as np
from tensorflow.contrib.layers import fully_connected
from tensorflow.contrib.rnn import BasicLSTMCell
from tensorflow.contrib.rnn import MultiRNNCell
from tensorflow.contrib.rnn import OutputProjectionWrapper
from tensorflow.contrib.rnn import DropoutWrapper
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()


is_training = (sys.argv[-1] == "train")
keep_prob = 0.5
n_steps = 100
n_inputs = 1
n_neurous = 100
n_outputs = 1

n_layers = 5

learning_rate = 0.00001

n_iterations = 10000
batch_size = 50


def make_rnn_cell():
    return BasicLSTMCell(num_units=n_neurous, activation=tf.nn.relu)


def make_drop_cell():
    return DropoutWrapper(make_rnn_cell(), input_keep_prob=keep_prob)


X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])

# 现在在每个时间迭代，有一个大小为100的输出向量，但是实际上我们需要一个单独的输出值。
# 最简单的解决方案是将单元格包装在OutputProjectionWrapper中。
# cell = OutputProjectionWrapper(BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu), output_size=n_outputs)

# 用技巧提高速度
layers = [make_rnn_cell() for _ in range(n_layers)]
# if is_training:
#     layers = [make_drop_cell() for _ in range(n_layers)]

multi_layer_cell = MultiRNNCell(layers)
rnn_outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurous])
stacked_outputs = fully_connected(stacked_rnn_outputs, n_outputs, activation_fn=None)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])

loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

X_data = np.linspace(0, 15, 101)

with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        X_batch = X_data[:-1][np.newaxis, :, np.newaxis]
        y_batch = X_batch * np.sin(X_batch) / 3 + 2 * np.sin(5 * X_batch)
        sess.run(training_op, feed_dict={
         X: X_batch, y: y_batch})
        if iteration % 100 == 0:
            mse = loss.eval(feed_dict={
         X: X_batch, y: y_batch})
            print(iteration, "\tMSE", mse)

    X_new = X_data[1:][np.newaxis, :, np.newaxis]
    y_true = X_new * np.sin(X_new) / 3 + 2 * np.sin(5 * X_new)
    y_pred = sess.run(outputs, feed_dict={
         X: X_new})

print(X_new.flatten())
print('真实结果：', y_true.flatten())
print('预测结果：', y_pred.flatten())

plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig = plt.figure(dpi=150)
plt.plot(X_new.flatten(), y_true.flatten(), 'r', label='y_true')
plt.plot(X_new.flatten(), y_pred.flatten(), 'b', label='y_pred')
plt.title('深层RNN预测')
plt.legend()
plt.show()

    • 运行结果

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第14张图片

  • 窥视孔连接

    • 窥视孔连接（peephole connections）：LSTM变体，当前一个长期状态 c ( t − 1 ) c_{(t-1)} c(t−1)​作为输入传入忘记门限和输入门限，当前的长期状态 c ( t ) c_{(t)} c(t)​作为输入传出门限控制器。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: lstm_test2.py
@time: 2019/6/19 16:36
@desc: 窥视孔连接
"""

import tensorflow as tf
import numpy as np
from tensorflow.contrib.layers import fully_connected
from tensorflow.contrib.rnn import LSTMCell
from tensorflow.contrib.rnn import MultiRNNCell
from tensorflow.contrib.rnn import OutputProjectionWrapper
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()


n_steps = 100
n_inputs = 1
n_neurous = 100
n_outputs = 1

n_layers = 10

learning_rate = 0.00001

n_iterations = 10000
batch_size = 50

X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])

# 现在在每个时间迭代，有一个大小为100的输出向量，但是实际上我们需要一个单独的输出值。
# 最简单的解决方案是将单元格包装在OutputProjectionWrapper中。
# cell = OutputProjectionWrapper(BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu), output_size=n_outputs)

# 用技巧提高速度
# cell = BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu)
# multi_layer_cell = MultiRNNCell([cell] * n_layers)
layers = [LSTMCell(num_units=n_neurous, activation=tf.nn.relu, use_peepholes=True) for _ in range(n_layers)]
multi_layer_cell = MultiRNNCell(layers)
rnn_outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurous])
stacked_outputs = fully_connected(stacked_rnn_outputs, n_outputs, activation_fn=None)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])

loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

X_data = np.linspace(0, 15, 101)
with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        X_batch = X_data[:-1][np.newaxis, :, np.newaxis]
        y_batch = X_batch * np.sin(X_batch) / 3 + 2 * np.sin(5 * X_batch)
        sess.run(training_op, feed_dict={
         X: X_batch, y: y_batch})
        if iteration % 100 == 0:
            mse = loss.eval(feed_dict={
         X: X_batch, y: y_batch})
            print(iteration, "\tMSE", mse)

    X_new = X_data[1:][np.newaxis, :, np.newaxis]
    y_true = X_new * np.sin(X_new) / 3 + 2 * np.sin(5 * X_new)
    y_pred = sess.run(outputs, feed_dict={
         X: X_new})

print(X_new.flatten())
print('真实结果：', y_true.flatten())
print('预测结果：', y_pred.flatten())

plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig = plt.figure(dpi=150)
plt.plot(X_new.flatten(), y_true.flatten(), 'r', label='y_true')
plt.plot(X_new.flatten(), y_pred.flatten(), 'b', label='y_pred')
plt.title('深层RNN预测')
plt.legend()
plt.show()

    • 运行结果

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第15张图片

  • GRU单元

    • GRU单元是LSTM的简化版本，其主要简化了：

      1. 两个状态向量合并为一个向量 h ( t ) h_{(t)} h(t)​。
      2. 一个门限控制器同时控制忘记门限和输入门限。如果门限控制器的输出是1，那么输入门限打开而忘记门限关闭。如果输出是0，则刚好相反。换句话说，无论何时需要存储一个记忆，它将被存在的位置将首先被擦除。这实际上是LSTM单元的一个常见变体。
      3. 没有输出门限。在每个时间迭代，输出向量的全部状态被直接输出。然而，GRU有一个新的门限控制器来控制前一个状态的哪部分将显示给主层。

  • GRU 是新一代的循环神经网络，与 LSTM 非常相似。与 LSTM 相比，GRU 去除掉了细胞状态，使用隐藏状态来进行信息的传递。它只包含两个门：更新门和重置门。

  • 更新门：更新门的作用类似于 LSTM 中的遗忘门和输入门。它决定了要忘记哪些信息以及哪些新信息需要被添加。

  • 重置门：重置门用于决定遗忘先前信息的程度。

  • GRU 的张量运算较少，因此它比 LSTM 的训练更快一下。很难去判定这两者到底谁更好，研究人员通常会两者都试一下，然后选择最合适的。

    #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: gru_test1.py
@time: 2019/6/19 17:07
@desc: GRU单元
"""

import tensorflow as tf
import numpy as np
from tensorflow.contrib.layers import fully_connected
from tensorflow.contrib.rnn import GRUCell
from tensorflow.contrib.rnn import MultiRNNCell
from tensorflow.contrib.rnn import OutputProjectionWrapper
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()


n_steps = 100
n_inputs = 1
n_neurous = 100
n_outputs = 1

n_layers = 10

learning_rate = 0.00001

n_iterations = 10000
batch_size = 50

X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])

# 现在在每个时间迭代，有一个大小为100的输出向量，但是实际上我们需要一个单独的输出值。
# 最简单的解决方案是将单元格包装在OutputProjectionWrapper中。
# cell = OutputProjectionWrapper(BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu), output_size=n_outputs)

# 用技巧提高速度
# cell = BasicRNNCell(num_units=n_neurous, activation=tf.nn.relu)
# multi_layer_cell = MultiRNNCell([cell] * n_layers)
layers = [GRUCell(num_units=n_neurous, activation=tf.nn.relu) for _ in range(n_layers)]
multi_layer_cell = MultiRNNCell(layers)
rnn_outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurous])
stacked_outputs = fully_connected(stacked_rnn_outputs, n_outputs, activation_fn=None)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])

loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

X_data = np.linspace(0, 15, 101)
with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        X_batch = X_data[:-1][np.newaxis, :, np.newaxis]
        y_batch = X_batch * np.sin(X_batch) / 3 + 2 * np.sin(5 * X_batch)
        sess.run(training_op, feed_dict={
       X: X_batch, y: y_batch})
        if iteration % 100 == 0:
            mse = loss.eval(feed_dict={
       X: X_batch, y: y_batch})
            print(iteration, "\tMSE", mse)

    X_new = X_data[1:][np.newaxis, :, np.newaxis]
    y_true = X_new * np.sin(X_new) / 3 + 2 * np.sin(5 * X_new)
    y_pred = sess.run(outputs, feed_dict={
       X: X_new})

print(X_new.flatten())
print('真实结果：', y_true.flatten())
print('预测结果：', y_pred.flatten())

plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig = plt.figure(dpi=150)
plt.plot(X_new.flatten(), y_true.flatten(), 'r', label='y_true')
plt.plot(X_new.flatten(), y_pred.flatten(), 'b', label='y_pred')
plt.title('GRU预测')
plt.legend()
plt.show()

    • 运行结果

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第16张图片

    参考链接：深入理解LSTM，窥视孔连接，GRU

    更好的参考链接：GRU与LSTM总结

  • 其他变形的LSTM网络总结

    参考链接：直观理解LSTM（长短时记忆网络）

    1. 窥视孔连接LSTM

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第17张图片

      一种流行的LSTM变种，由Gers和Schmidhuber （2000）提出，加入了“窥视孔连接”（peephole connections）。这意味着门限层也将单元状态作为输入。

    2. 耦合遗忘输入门限的LSTM

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第18张图片

      就是使用耦合遗忘和输入门限。我们不单独决定遗忘哪些、添加哪些新信息，而是一起做出决定。在输入的时候才进行遗忘。在遗忘某些旧信息时才将新值添加到状态中。

    3. 门限递归单元（GRU）

      《机器学习实战——基于Scikit-Learn和TensorFlow》学习笔记_第19张图片

      它将遗忘和输入门限结合输入到单个“更新门限”中。同样还将单元状态和隐藏状态合并，并做出一些其他变化。所得模型比标准LSTM模型要简单，这种做法越来越流行。

  • 部分课后题的摘抄

    • 在构建RNN时使用dynamic_rnn()而不是static_rnn()的优势是什么？

      1. 它基于while_loop()操作，可以在反向传播期间将GPU内存交互到CPU内存，从而避免了内存溢出。
      2. 它更加易于使用，因为其采取单张量作为输入和输出（覆盖所有时间步长），而不是一个张量列表（每个时间一个步长）。不需要入栈、出栈，或转置。
      3. 它产生的图形更小，更容易在TensorBoard中可视化。

    • 如何处理变长输入序列？变长输出序列又会怎么样？

      1. 为了处理可变长度的输入序列，最简单的方法是在调用static_rnn()或dynamic_rnn()方法时传入sequence_length参数。另一个方法是填充长度较小的输入（比如，用0填充）来使其与最大输入长度相同（这可能比第一种方法快，因为所有输入序列具有相同的长度）。

      2. 为了处理可变长度的输出序列，如果事先知道每个输出序列的长度，就可以使用sequence_length参数（例如，序列到序列RNN使用暴力评分标记视频中的每一帧：输出序列和输入序列长度完全一致）。如果事先不知道输出序列的长度，则可以使用填充方法：始终输出相同大小的序列，但是忽略end-of-sequence标记之后的任何输出（在计算成本函数时忽略它们）。

    • 在多个GPU之间分配训练和执行层次RNN的常见方式是什么？

      为了在多个GPU直接分配训练并执行深度RNN，一个常用的简单技术是将每个层放在不同的GPU上。

15. 自动编码器

  • 使用不完整的线性自动编码器实现PCA

    • 一个自动编码器由两部分组成：编码器（或称为识别网络），解码器（或称为生成网络）。

    • 输出层的神经元数量必须等于输入层的数量。

    • 输出通常被称为重建，因为自动编码器尝试重建输入，并且成本函数包含重建损失，当重建与输入不同时，该损失会惩罚模型。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_1.py
@time: 2019/6/20 14:31
@desc: 使用不完整的线性自动编码器实现PCA
"""

import tensorflow as tf
from tensorflow.contrib.layers import fully_connected
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d

# 生成数据
import numpy.random as rnd

rnd.seed(4)
m = 200
w1, w2 = 0.1, 0.3
noise = 0.1

angles = rnd.rand(m) * 3 * np.pi / 2 - 0.5
data = np.empty((m, 3))
data[:, 0] = np.cos(angles) + np.sin(angles) / 2 + noise * rnd.randn(m) / 2
data[:, 1] = np.sin(angles) * 0.7 + noise * rnd.randn(m) / 2
data[:, 2] = data[:, 0] * w1 + data[:, 1] * w2 + noise * rnd.randn(m)

# 数据标准化
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train = scaler.fit_transform(data[:100])
X_test = scaler.transform(data[100:])

# 3D inputs
n_inputs = 3
# 2D codings
n_hidden = 2

n_outputs = n_inputs

learning_rate = 0.01

n_iterations = 1000

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden = fully_connected(X, n_hidden, activation_fn=None)
outputs = fully_connected(hidden, n_outputs, activation_fn=None)

# MSE
reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))

optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(reconstruction_loss)

init = tf.global_variables_initializer()
codings = hidden

with tf.Session() as sess:
    init.run()
    for n_iterations in range(n_iterations):
        training_op.run(feed_dict={
         X: X_train})
    codings_val = codings.eval(feed_dict={
         X: X_test})

fig = plt.figure(figsize=(4, 3), dpi=300)
plt.plot(codings_val[:, 0], codings_val[:, 1], "b.")
plt.xlabel("$z_1$", fontsize=18)
plt.ylabel("$z_2$", fontsize=18, rotation=0)
plt.show()

    • 运行结果

      img

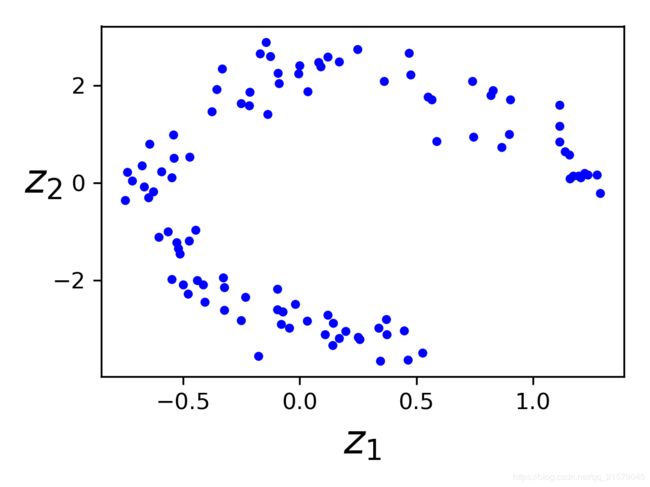
    • 画出的是中间两个神经元隐藏层。（降维）

  • 栈式自动编码器（深度自动编码器）

    • 使用He初始化，ELU激活函数，以及 l 2 l_2 l2​正则化构建了一个MNIST栈式自动编码器。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_2.py
@time: 2019/6/21 8:48
@desc: 使用He初始化，ELU激活函数，以及$l_2$正则化构建了一个MNIST栈式自动编码器
"""

import tensorflow as tf
from tensorflow.contrib.layers import fully_connected
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
import sys


n_inputs = 28 * 28      # for MNIST
n_hidden1 = 300
n_hidden2 = 150         # codings
n_hidden3 = n_hidden1
n_outputs = n_inputs

learning_rate = 0.001
l2_reg = 0.001

n_epochs = 30
batch_size = 150

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
with tf.contrib.framework.arg_scope(
    [fully_connected],
    activation_fn=tf.nn.elu,
    weights_initializer=tf.contrib.layers.variance_scaling_initializer(),
    weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg)
):
    hidden1 = fully_connected(X, n_hidden1)
    hidden2 = fully_connected(hidden1, n_hidden2)   # codings
    hidden3 = fully_connected(hidden2, n_hidden3)
    outputs = fully_connected(hidden3, n_outputs, activation_fn=None)

reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))    # MSE

reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
loss = tf.add_n([reconstruction_loss] + reg_losses)

optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()
saver = tf.train.Saver()

with tf.Session() as sess:
    mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')
    init.run()
    for epoch in range(n_epochs):
        n_batches = mnist.train.num_examples // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={
         X: X_batch})
        loss_train = reconstruction_loss.eval(feed_dict={
         X: X_batch})
        print("\r{}".format(epoch), "Train MSE:", loss_train)
        saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_all_layers.ckpt")


# 可视化
def plot_image(image, shape=[28, 28]):
    plt.imshow(image.reshape(shape), cmap="Greys", interpolation="nearest")
    plt.axis("off")


def show_reconstructed_digits(X, outputs, model_path = None, n_test_digits = 2):
    with tf.Session() as sess:
        if model_path:
            saver.restore(sess, model_path)
        X_test = mnist.test.images[:n_test_digits]
        outputs_val = outputs.eval(feed_dict={
         X: X_test})

    fig = plt.figure(figsize=(8, 3 * n_test_digits))
    for digit_index in range(n_test_digits):
        plt.subplot(n_test_digits, 2, digit_index * 2 + 1)
        plot_image(X_test[digit_index])
        plt.subplot(n_test_digits, 2, digit_index * 2 + 2)
        plot_image(outputs_val[digit_index])
    plt.show()


show_reconstructed_digits(X, outputs, "D:/Python3Space/BookStudy/book4/model/my_model_all_layers.ckpt")

    • 运行结果

    img

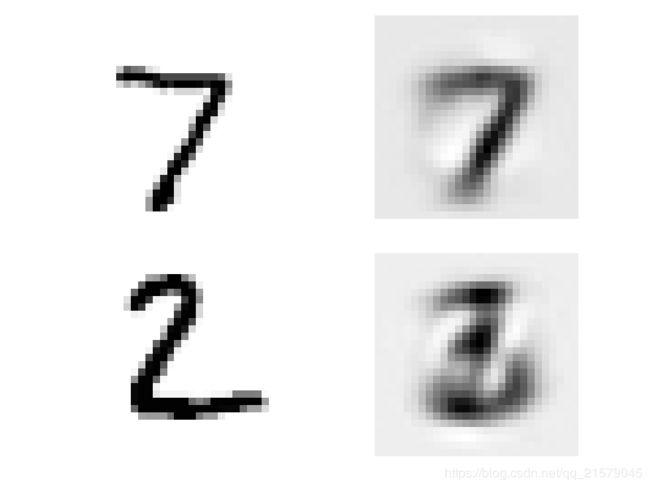
  • 权重绑定

    • 将解码层的权重和编码层的权重联系起来。 W N − L + 1 = W L T W_{N-L+1} = W_L^T WN−L+1​=WLT​

    • weight3和weights4不是变量，它们分别是weights2和weights1的转置（它们被“绑定”在一起）。

    • 因为它们不是变量，所以没有必要进行正则化，只正则化weights1和weigts2。

    • 偏置项从来不会被绑定，也不会被正则化。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_3.py
@time: 2019/6/21 9:48
@desc: 权重绑定
"""

import tensorflow as tf
from tensorflow.contrib.layers import fully_connected
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
import sys


# 在复制一遍可视化代码
def plot_image(image, shape=[28, 28]):
    plt.imshow(image.reshape(shape), cmap="Greys", interpolation="nearest")
    plt.axis("off")


def show_reconstructed_digits(X, outputs, model_path = None, n_test_digits = 2):
    with tf.Session() as sess:
        if model_path:
            saver.restore(sess, model_path)
        X_test = mnist.test.images[:n_test_digits]
        outputs_val = outputs.eval(feed_dict={
         X: X_test})

    fig = plt.figure(figsize=(8, 3 * n_test_digits))
    for digit_index in range(n_test_digits):
        plt.subplot(n_test_digits, 2, digit_index * 2 + 1)
        plot_image(X_test[digit_index])
        plt.subplot(n_test_digits, 2, digit_index * 2 + 2)
        plot_image(outputs_val[digit_index])
    plt.show()


n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 150  # codings
n_hidden3 = n_hidden1
n_outputs = n_inputs

learning_rate = 0.01
l2_reg = 0.001

n_epochs = 5
batch_size = 150

activation = tf.nn.elu
regularizer = tf.contrib.layers.l2_regularizer(l2_reg)
initializer = tf.contrib.layers.variance_scaling_initializer()

X = tf.placeholder(tf.float32, shape=[None, n_inputs])

weights1_init = initializer([n_inputs, n_hidden1])
weights2_init = initializer([n_hidden1, n_hidden2])

weights1 = tf.Variable(weights1_init, dtype=tf.float32, name='weights1')
weights2 = tf.Variable(weights2_init, dtype=tf.float32, name='weights2')
weights3 = tf.transpose(weights2, name='weights3')      # 权重绑定
weights4 = tf.transpose(weights1, name='weights4')      # 权重绑定

biases1 = tf.Variable(tf.zeros(n_hidden1), name='biases1')
biases2 = tf.Variable(tf.zeros(n_hidden2), name='biases2')
biases3 = tf.Variable(tf.zeros(n_hidden3), name='biases3')
biases4 = tf.Variable(tf.zeros(n_outputs), name='biases4')

hidden1 = activation(tf.matmul(X, weights1) + biases1)
hidden2 = activation(tf.matmul(hidden1, weights2) + biases2)
hidden3 = activation(tf.matmul(hidden2, weights3) + biases3)
outputs = tf.matmul(hidden3, weights4) + biases4

reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))
reg_loss = regularizer(weights1) + regularizer(weights2)
loss = reconstruction_loss + reg_loss

optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()
saver = tf.train.Saver()

with tf.Session() as sess:
    mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')
    init.run()
    for epoch in range(n_epochs):
        n_batches = mnist.train.num_examples // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={
         X: X_batch})
        loss_train = reconstruction_loss.eval(feed_dict={
         X: X_batch})
        print("\r{}".format(epoch), "Train MSE:", loss_train)
        saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_tying_weights.ckpt")

show_reconstructed_digits(X, outputs, "D:/Python3Space/BookStudy/book4/model/my_model_tying_weights.ckpt")

    • 运行结果

    img

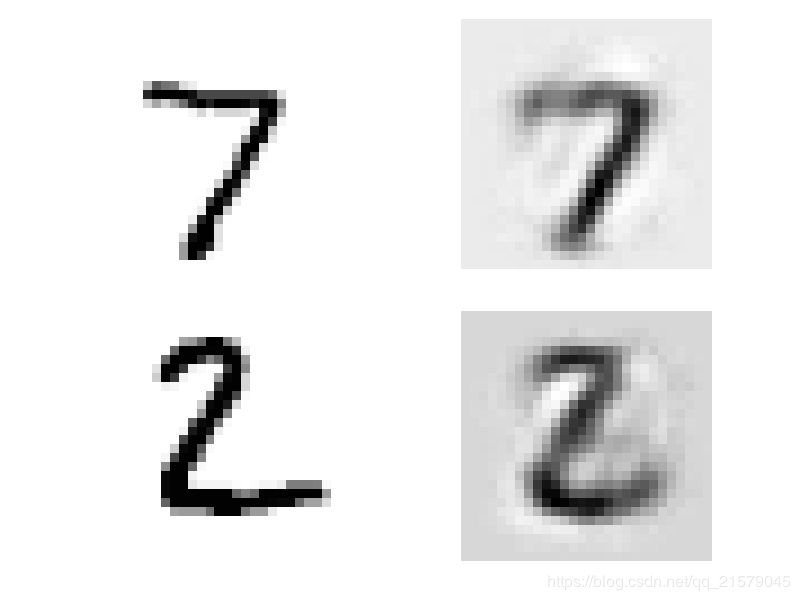
  • 在多个图中一次训练一个自动编码器

    • 有许多方法可以一次训练一个自动编码器。第一种方法是使用不同的图形对每个自动编码器进行训练，然后我们通过简单地初始化它和从这些自动编码器复制的权重和偏差来创建堆叠的自动编码器。

    • 让我们创建一个函数来训练一个自动编码器并返回转换后的训练集(即隐藏层的输出)和模型参数。

    • 现在让我们训练两个自动编码器。第一个是关于训练数据的训练，第二个是关于上一个自动编码器隐藏层输出的训练。

    • 最后，通过简单地重用我们刚刚训练的自动编码器的权重和偏差，我们可以创建一个堆叠的自动编码器。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_6.py
@time: 2019/6/24 10:29
@desc: 在多个图中一次训练一个自动编码器
"""

import tensorflow as tf
from tensorflow.contrib.layers import fully_connected
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
import sys
import numpy.random as rnd

from functools import partial


# 在复制一遍可视化代码
def plot_image(image, shape=[28, 28]):
    plt.imshow(image.reshape(shape), cmap="Greys", interpolation="nearest")
    plt.axis("off")


def show_reconstructed_digits(X, outputs, n_test_digits=2):
    with tf.Session() as sess:
        # if model_path:
        #     saver.restore(sess, model_path)
        X_test = mnist.test.images[:n_test_digits]
        outputs_val = outputs.eval(feed_dict={
         X: X_test})

    fig = plt.figure(figsize=(8, 3 * n_test_digits))
    for digit_index in range(n_test_digits):
        plt.subplot(n_test_digits, 2, digit_index * 2 + 1)
        plot_image(X_test[digit_index])
        plt.subplot(n_test_digits, 2, digit_index * 2 + 2)
        plot_image(outputs_val[digit_index])
    plt.show()


# 有许多方法可以一次训练一个自动编码器。第一种方法是使用不同的图形对每个自动编码器进行训练，
# 然后我们通过简单地初始化它和从这些自动编码器复制的权重和偏差来创建堆叠的自动编码器。
def train_autoencoder(X_train, n_neurons, n_epochs, batch_size,
                      learning_rate=0.01, l2_reg=0.0005,
                      activation=tf.nn.elu, seed=42):
    graph = tf.Graph()
    with graph.as_default():
        tf.set_random_seed(seed)

        n_inputs = X_train.shape[1]

        X = tf.placeholder(tf.float32, shape=[None, n_inputs])

        my_dense_layer = partial(
            tf.layers.dense,
            activation=activation,
            kernel_initializer=tf.contrib.layers.variance_scaling_initializer(),
            kernel_regularizer=tf.contrib.layers.l2_regularizer(l2_reg))

        hidden = my_dense_layer(X, n_neurons, name="hidden")
        outputs = my_dense_layer(hidden, n_inputs, activation=None, name="outputs")

        reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))

        reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
        loss = tf.add_n([reconstruction_loss] + reg_losses)

        optimizer = tf.train.AdamOptimizer(learning_rate)
        training_op = optimizer.minimize(loss)

        init = tf.global_variables_initializer()

    with tf.Session(graph=graph) as sess:
        init.run()
        for epoch in range(n_epochs):
            n_batches = len(X_train) // batch_size
            for iteration in range(n_batches):
                print("\r{}%".format(100 * iteration // n_batches), end="")
                sys.stdout.flush()
                indices = rnd.permutation(len(X_train))[:batch_size]
                X_batch = X_train[indices]
                sess.run(training_op, feed_dict={
         X: X_batch})
            loss_train = reconstruction_loss.eval(feed_dict={
         X: X_batch})
            print("\r{}".format(epoch), "Train MSE:", loss_train)
        params = dict([(var.name, var.eval()) for var in tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES)])
        hidden_val = hidden.eval(feed_dict={
         X: X_train})
        return hidden_val, params["hidden/kernel:0"], params["hidden/bias:0"], params["outputs/kernel:0"], params["outputs/bias:0"]


mnist = input_data.read_data_sets('F:/JupyterWorkspace/MNIST_data/')
hidden_output, W1, b1, W4, b4 = train_autoencoder(mnist.train.images, n_neurons=300, n_epochs=4, batch_size=150)
_, W2, b2, W3, b3 = train_autoencoder(hidden_output, n_neurons=150, n_epochs=4, batch_size=150)

# 最后，通过简单地重用我们刚刚训练的自动编码器的权重和偏差，我们可以创建一个堆叠的自动编码器。
n_inputs = 28*28

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden1 = tf.nn.elu(tf.matmul(X, W1) + b1)
hidden2 = tf.nn.elu(tf.matmul(hidden1, W2) + b2)
hidden3 = tf.nn.elu(tf.matmul(hidden2, W3) + b3)
outputs = tf.matmul(hidden3, W4) + b4

show_reconstructed_digits(X, outputs)

    • 运行结果

    img

  • 在一个图中一次训练一个自动编码器

    • 另一种方法是使用单个图。为此，我们为完整的堆叠式自动编码器创建了图形，但是我们还添加了独立训练每个自动编码器的操作：第一阶段训练底层和顶层(即。第一个自动编码器和第二阶段训练两个中间层(即。第二个自动编码器)。

    • 通过设置optimizer.minimize参数中的var_list，达到freeze其他权重的目的。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_7.py
@time: 2019/7/2 9:02
@desc: 在一个图中一次训练一个自动编码器
"""

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
import sys
import numpy.random as rnd

from functools import partial


n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 150  # codings
n_hidden3 = n_hidden1
n_outputs = n_inputs

learning_rate = 0.01
l2_reg = 0.0001

activation = tf.nn.elu
regularizer = tf.contrib.layers.l2_regularizer(l2_reg)
initializer = tf.contrib.layers.variance_scaling_initializer()

X = tf.placeholder(tf.float32, shape=[None, n_inputs])

weights1_init = initializer([n_inputs, n_hidden1])
weights2_init = initializer([n_hidden1, n_hidden2])
weights3_init = initializer([n_hidden2, n_hidden3])
weights4_init = initializer([n_hidden3, n_outputs])

weights1 = tf.Variable(weights1_init, dtype=tf.float32, name="weights1")
weights2 = tf.Variable(weights2_init, dtype=tf.float32, name="weights2")
weights3 = tf.Variable(weights3_init, dtype=tf.float32, name="weights3")
weights4 = tf.Variable(weights4_init, dtype=tf.float32, name="weights4")

biases1 = tf.Variable(tf.zeros(n_hidden1), name="biases1")
biases2 = tf.Variable(tf.zeros(n_hidden2), name="biases2")
biases3 = tf.Variable(tf.zeros(n_hidden3), name="biases3")
biases4 = tf.Variable(tf.zeros(n_outputs), name="biases4")

hidden1 = activation(tf.matmul(X, weights1) + biases1)
hidden2 = activation(tf.matmul(hidden1, weights2) + biases2)
hidden3 = activation(tf.matmul(hidden2, weights3) + biases3)
outputs = tf.matmul(hidden3, weights4) + biases4

reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))

optimizer = tf.train.AdamOptimizer(learning_rate)


# 第一阶段
with tf.name_scope("phase1"):
    phase1_outputs = tf.matmul(hidden1, weights4) + biases4  # bypass hidden2 and hidden3
    phase1_reconstruction_loss = tf.reduce_mean(tf.square(phase1_outputs - X))
    phase1_reg_loss = regularizer(weights1) + regularizer(weights4)
    phase1_loss = phase1_reconstruction_loss + phase1_reg_loss
    phase1_training_op = optimizer.minimize(phase1_loss)


# 第二阶段
with tf.name_scope("phase2"):
    phase2_reconstruction_loss = tf.reduce_mean(tf.square(hidden3 - hidden1))
    phase2_reg_loss = regularizer(weights2) + regularizer(weights3)
    phase2_loss = phase2_reconstruction_loss + phase2_reg_loss
    train_vars = [weights2, biases2, weights3, biases3]
    phase2_training_op = optimizer.minimize(phase2_loss, var_list=train_vars)   # freeze hidden1


init = tf.global_variables_initializer()
saver = tf.train.Saver()

training_ops = [phase1_training_op, phase2_training_op]
reconstruction_losses = [phase1_reconstruction_loss, phase2_reconstruction_loss]
n_epochs = [4, 4]
batch_sizes = [150, 150]


with tf.Session() as sess:
    mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')
    init.run()
    for phase in range(2):
        print("Training phase #{}".format(phase + 1))
        for epoch in range(n_epochs[phase]):
            n_batches = mnist.train.num_examples // batch_sizes[phase]
            for iteration in range(n_batches):
                print("\r{}%".format(100 * iteration // n_batches), end="")
                sys.stdout.flush()
                X_batch, y_batch = mnist.train.next_batch(batch_sizes[phase])
                sess.run(training_ops[phase], feed_dict={
         X: X_batch})
            loss_train = reconstruction_losses[phase].eval(feed_dict={
         X: X_batch})
            print("\r{}".format(epoch), "Train MSE:", loss_train)
            saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_one_at_a_time.ckpt")
    loss_test = reconstruction_loss.eval(feed_dict={
         X: mnist.test.images})
    print("Test MSE:", loss_test)

    • 运行结果：

      img

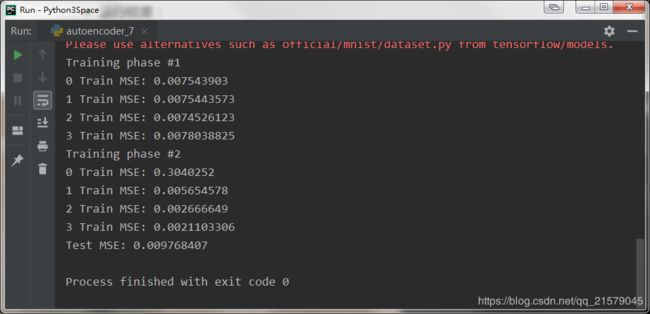
  • 馈送冻结层输出缓存

    • 由于隐藏层 1 在阶段 2 期间被冻结，所以对于任何给定的训练实例其输出将总是相同的。为了避免在每个时期重新计算隐藏层1的输出，可以在阶段 1 结束时为整个训练集计算它，然后直接在阶段 2 中输入隐藏层 1 的缓存输出。这可以得到一个不错的性能上的提升。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_8.py
@time: 2019/7/2 9:32
@desc: 馈送冻结层输出缓存
"""

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy.random as rnd
import sys


n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 150  # codings
n_hidden3 = n_hidden1
n_outputs = n_inputs

learning_rate = 0.01
l2_reg = 0.0001

activation = tf.nn.elu
regularizer = tf.contrib.layers.l2_regularizer(l2_reg)
initializer = tf.contrib.layers.variance_scaling_initializer()

X = tf.placeholder(tf.float32, shape=[None, n_inputs])

weights1_init = initializer([n_inputs, n_hidden1])
weights2_init = initializer([n_hidden1, n_hidden2])
weights3_init = initializer([n_hidden2, n_hidden3])
weights4_init = initializer([n_hidden3, n_outputs])

weights1 = tf.Variable(weights1_init, dtype=tf.float32, name="weights1")
weights2 = tf.Variable(weights2_init, dtype=tf.float32, name="weights2")
weights3 = tf.Variable(weights3_init, dtype=tf.float32, name="weights3")
weights4 = tf.Variable(weights4_init, dtype=tf.float32, name="weights4")

biases1 = tf.Variable(tf.zeros(n_hidden1), name="biases1")
biases2 = tf.Variable(tf.zeros(n_hidden2), name="biases2")
biases3 = tf.Variable(tf.zeros(n_hidden3), name="biases3")
biases4 = tf.Variable(tf.zeros(n_outputs), name="biases4")

hidden1 = activation(tf.matmul(X, weights1) + biases1)
hidden2 = activation(tf.matmul(hidden1, weights2) + biases2)
hidden3 = activation(tf.matmul(hidden2, weights3) + biases3)
outputs = tf.matmul(hidden3, weights4) + biases4

reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))

optimizer = tf.train.AdamOptimizer(learning_rate)


# 第一阶段
with tf.name_scope("phase1"):
    phase1_outputs = tf.matmul(hidden1, weights4) + biases4  # bypass hidden2 and hidden3
    phase1_reconstruction_loss = tf.reduce_mean(tf.square(phase1_outputs - X))
    phase1_reg_loss = regularizer(weights1) + regularizer(weights4)
    phase1_loss = phase1_reconstruction_loss + phase1_reg_loss
    phase1_training_op = optimizer.minimize(phase1_loss)


# 第二阶段
with tf.name_scope("phase2"):
    phase2_reconstruction_loss = tf.reduce_mean(tf.square(hidden3 - hidden1))
    phase2_reg_loss = regularizer(weights2) + regularizer(weights3)
    phase2_loss = phase2_reconstruction_loss + phase2_reg_loss
    train_vars = [weights2, biases2, weights3, biases3]
    phase2_training_op = optimizer.minimize(phase2_loss, var_list=train_vars)   # freeze hidden1


init = tf.global_variables_initializer()
saver = tf.train.Saver()

training_ops = [phase1_training_op, phase2_training_op]
reconstruction_losses = [phase1_reconstruction_loss, phase2_reconstruction_loss]
n_epochs = [4, 4]
batch_sizes = [150, 150]

with tf.Session() as sess:
    mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')
    init.run()
    for phase in range(2):
        print("Training phase #{}".format(phase + 1))
        if phase == 1:
            hidden1_cache = hidden1.eval(feed_dict={
         X: mnist.train.images})
        for epoch in range(n_epochs[phase]):
            n_batches = mnist.train.num_examples // batch_sizes[phase]
            for iteration in range(n_batches):
                print("\r{}%".format(100 * iteration // n_batches), end="")
                sys.stdout.flush()
                if phase == 1:
                    indices = rnd.permutation(mnist.train.num_examples)
                    hidden1_batch = hidden1_cache[indices[:batch_sizes[phase]]]
                    feed_dict = {
         hidden1: hidden1_batch}
                    sess.run(training_ops[phase], feed_dict=feed_dict)
                else:
                    X_batch, y_batch = mnist.train.next_batch(batch_sizes[phase])
                    feed_dict = {
         X: X_batch}
                    sess.run(training_ops[phase], feed_dict=feed_dict)
            loss_train = reconstruction_losses[phase].eval(feed_dict=feed_dict)
            print("\r{}".format(epoch), "Train MSE:", loss_train)
            saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_cache_frozen.ckpt")
    loss_test = reconstruction_loss.eval(feed_dict={
         X: mnist.test.images})
    print("Test MSE:", loss_test)

    • 运行结果：

      img

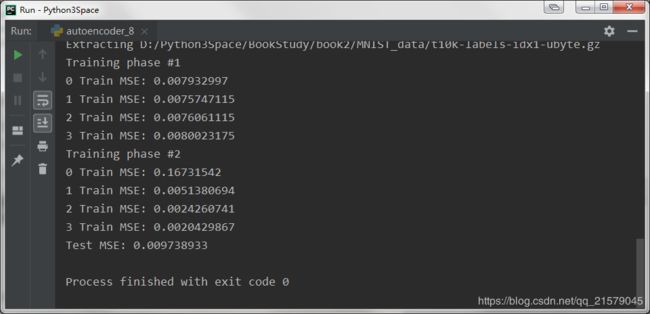
  • 重建可视化

    • 确保自编码器得到适当训练的一种方法是比较输入和输出。 它们必须非常相似，差异应该是不重要的细节。 我们来绘制两个随机数字及其重建：

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_9.py
@time: 2019/7/2 9:38
@desc: 重建可视化
"""
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt


n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 150  # codings
n_hidden3 = n_hidden1
n_outputs = n_inputs

learning_rate = 0.01
l2_reg = 0.0001

activation = tf.nn.elu
regularizer = tf.contrib.layers.l2_regularizer(l2_reg)
initializer = tf.contrib.layers.variance_scaling_initializer()

X = tf.placeholder(tf.float32, shape=[None, n_inputs])

weights1_init = initializer([n_inputs, n_hidden1])
weights2_init = initializer([n_hidden1, n_hidden2])
weights3_init = initializer([n_hidden2, n_hidden3])
weights4_init = initializer([n_hidden3, n_outputs])

weights1 = tf.Variable(weights1_init, dtype=tf.float32, name="weights1")
weights2 = tf.Variable(weights2_init, dtype=tf.float32, name="weights2")
weights3 = tf.Variable(weights3_init, dtype=tf.float32, name="weights3")
weights4 = tf.Variable(weights4_init, dtype=tf.float32, name="weights4")

biases1 = tf.Variable(tf.zeros(n_hidden1), name="biases1")
biases2 = tf.Variable(tf.zeros(n_hidden2), name="biases2")
biases3 = tf.Variable(tf.zeros(n_hidden3), name="biases3")
biases4 = tf.Variable(tf.zeros(n_outputs), name="biases4")

hidden1 = activation(tf.matmul(X, weights1) + biases1)
hidden2 = activation(tf.matmul(hidden1, weights2) + biases2)
hidden3 = activation(tf.matmul(hidden2, weights3) + biases3)
outputs = tf.matmul(hidden3, weights4) + biases4


mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')
n_test_digits = 2
X_test = mnist.test.images[:n_test_digits]

saver = tf.train.Saver()

with tf.Session() as sess:
    saver.restore(sess, "D:/Python3Space/BookStudy/book4/model/my_model_one_at_a_time.ckpt") # not shown in the book
    outputs_val = outputs.eval(feed_dict={
         X: X_test})


def plot_image(image, shape=[28, 28]):
    plt.imshow(image.reshape(shape), cmap="Greys", interpolation="nearest")
    plt.axis("off")


for digit_index in range(n_test_digits):
    plt.subplot(n_test_digits, 2, digit_index * 2 + 1)
    plot_image(X_test[digit_index])
    plt.subplot(n_test_digits, 2, digit_index * 2 + 2)
    plot_image(outputs_val[digit_index])

plt.show()

    • 运行结果：

      img

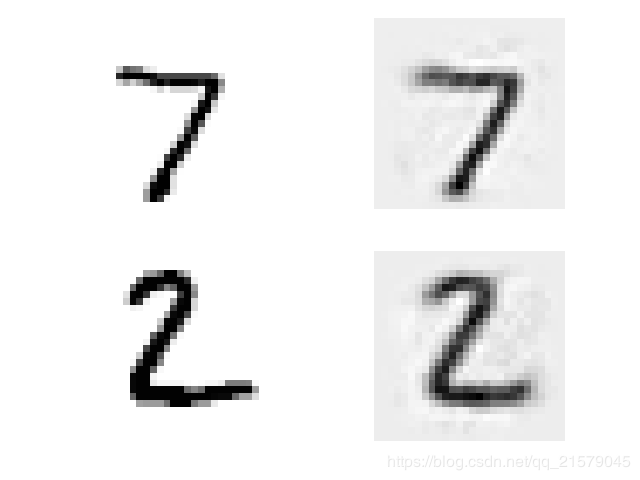
  • 特征可视化

    • 一旦你的自编码器学习了一些功能，你可能想看看它们。 有各种各样的技术。 可以说最简单的技术是在每个隐藏层中考虑每个神经元，并找到最能激活它的训练实例。

    • 对于第一个隐藏层中的每个神经元，您可以创建一个图像，其中像素的强度对应于给定神经元的连接权重。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_10.py
@time: 2019/7/2 9:49
@desc:  特征可视化
"""

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt


n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 150  # codings
n_hidden3 = n_hidden1
n_outputs = n_inputs

learning_rate = 0.01
l2_reg = 0.0001

activation = tf.nn.elu
regularizer = tf.contrib.layers.l2_regularizer(l2_reg)
initializer = tf.contrib.layers.variance_scaling_initializer()

X = tf.placeholder(tf.float32, shape=[None, n_inputs])

weights1_init = initializer([n_inputs, n_hidden1])
weights2_init = initializer([n_hidden1, n_hidden2])
weights3_init = initializer([n_hidden2, n_hidden3])
weights4_init = initializer([n_hidden3, n_outputs])

weights1 = tf.Variable(weights1_init, dtype=tf.float32, name="weights1")
weights2 = tf.Variable(weights2_init, dtype=tf.float32, name="weights2")
weights3 = tf.Variable(weights3_init, dtype=tf.float32, name="weights3")
weights4 = tf.Variable(weights4_init, dtype=tf.float32, name="weights4")

biases1 = tf.Variable(tf.zeros(n_hidden1), name="biases1")
biases2 = tf.Variable(tf.zeros(n_hidden2), name="biases2")
biases3 = tf.Variable(tf.zeros(n_hidden3), name="biases3")
biases4 = tf.Variable(tf.zeros(n_outputs), name="biases4")

hidden1 = activation(tf.matmul(X, weights1) + biases1)
hidden2 = activation(tf.matmul(hidden1, weights2) + biases2)
hidden3 = activation(tf.matmul(hidden2, weights3) + biases3)
outputs = tf.matmul(hidden3, weights4) + biases4

saver = tf.train.Saver()


# 在复制一遍可视化代码
def plot_image(image, shape=[28, 28]):
    plt.imshow(image.reshape(shape), cmap="Greys", interpolation="nearest")
    plt.axis("off")


with tf.Session() as sess:
    saver.restore(sess, "D:/Python3Space/BookStudy/book4/model/my_model_one_at_a_time.ckpt") # not shown in the book
    weights1_val = weights1.eval()

for i in range(5):
    plt.subplot(1, 5, i + 1)
    plot_image(weights1_val.T[i])

plt.show()

    • 运行结果：

      img

    • 第一层隐藏层为300个神经元，权重为[28*28, 300]。

    • 图中为可视化前五个神经元。

  • 使用堆叠的自动编码器进行无监督的预训练

    • 参考链接：Numpy.random中shuffle与permutation的区别

    • 函数shuffle与permutation都是对原来的数组进行重新洗牌（即随机打乱原来的元素顺序）；区别在于shuffle直接在原来的数组上进行操作，改变原来数组的顺序，无返回值。而permutation不直接在原来的数组上进行操作，而是返回一个新的打乱顺序的数组，并不改变原来的数组。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_4.py
@time: 2019/6/23 16:50
@desc: 使用堆叠的自动编码器进行无监督的预训练
"""

import tensorflow as tf
from tensorflow.contrib.layers import fully_connected
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
import sys
import numpy.random as rnd

n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 150
n_outputs = 10

learning_rate = 0.01
l2_reg = 0.0005

activation = tf.nn.elu
regularizer = tf.contrib.layers.l2_regularizer(l2_reg)
initializer = tf.contrib.layers.variance_scaling_initializer()

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
y = tf.placeholder(tf.int32, shape=[None])

weights1_init = initializer([n_inputs, n_hidden1])
weights2_init = initializer([n_hidden1, n_hidden2])
weights3_init = initializer([n_hidden2, n_outputs])

weights1 = tf.Variable(weights1_init, dtype=tf.float32, name="weights1")
weights2 = tf.Variable(weights2_init, dtype=tf.float32, name="weights2")
weights3 = tf.Variable(weights3_init, dtype=tf.float32, name="weights3")

biases1 = tf.Variable(tf.zeros(n_hidden1), name="biases1")
biases2 = tf.Variable(tf.zeros(n_hidden2), name="biases2")
biases3 = tf.Variable(tf.zeros(n_outputs), name="biases3")

hidden1 = activation(tf.matmul(X, weights1) + biases1)
hidden2 = activation(tf.matmul(hidden1, weights2) + biases2)
logits = tf.matmul(hidden2, weights3) + biases3

cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
reg_loss = regularizer(weights1) + regularizer(weights2) + regularizer(weights3)
loss = cross_entropy + reg_loss
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)

correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()
pretrain_saver = tf.train.Saver([weights1, weights2, biases1, biases2])
saver = tf.train.Saver()

n_epochs = 4
batch_size = 150
n_labeled_instances = 20000

with tf.Session() as sess:
    mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')
    init.run()
    for epoch in range(n_epochs):
        n_batches = n_labeled_instances // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            indices = rnd.permutation(n_labeled_instances)[:batch_size]
            X_batch, y_batch = mnist.train.images[indices], mnist.train.labels[indices]
            sess.run(training_op, feed_dict={
         X: X_batch, y: y_batch})
        accuracy_val = accuracy.eval(feed_dict={
         X: X_batch, y: y_batch})
        print("\r{}".format(epoch), "Train accuracy:", accuracy_val, end=" ")
        saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_supervised.ckpt")
        accuracy_val = accuracy.eval(feed_dict={
         X: mnist.test.images, y: mnist.test.labels})
        print("Test accuracy:", accuracy_val)

    • 运行结果

      img

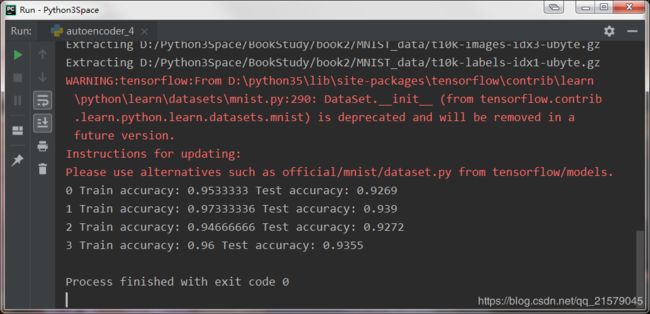
  • 去噪自动编码器

    • 另一种强制自动编码器学习有用特征的方法是在输入中增加噪音，训练它以恢复原始的无噪音输入。这种方法阻止了自动编码器简单的复制其输入到输出，最终必须找到数据中的模式。

    • 自动编码器可以用于特征提取。

    • 这里要用tf.shape(X)来获取图片的size，它创建了一个在运行时返回该点完全定义的X向量的操作；而不能用X.get_shape()，因为这将只返回部分定义的X([None], n_inputs)向量。

    • 使用高斯噪音

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_11.py
@time: 2019/7/2 10:02
@desc: 去噪自动编码器：使用高斯噪音
"""
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import sys


n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 150  # codings
n_hidden3 = n_hidden1
n_outputs = n_inputs

learning_rate = 0.01

noise_level = 1.0

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
X_noisy = X + noise_level * tf.random_normal(tf.shape(X))

hidden1 = tf.layers.dense(X_noisy, n_hidden1, activation=tf.nn.relu,
                          name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, # not shown in the book
                          name="hidden2")                            # not shown
hidden3 = tf.layers.dense(hidden2, n_hidden3, activation=tf.nn.relu, # not shown
                          name="hidden3")                            # not shown
outputs = tf.layers.dense(hidden3, n_outputs, name="outputs")        # not shown

reconstruction_loss = tf.reduce_mean(tf.square(outputs - X)) # MSE

optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(reconstruction_loss)

init = tf.global_variables_initializer()
saver = tf.train.Saver()

n_epochs = 10
batch_size = 150
mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')


with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        n_batches = mnist.train.num_examples // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={
         X: X_batch})
        loss_train = reconstruction_loss.eval(feed_dict={
         X: X_batch})
        print("\r{}".format(epoch), "Train MSE:", loss_train)
        saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_stacked_denoising_gaussian.ckpt")

    • 运行结果：

      img

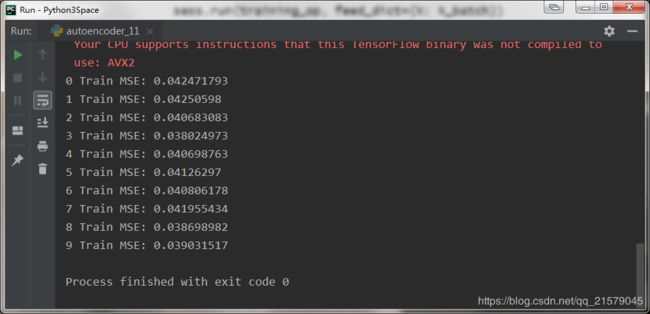
    • 使用dropout

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_12.py
@time: 2019/7/2 10:11
@desc: 去噪自动编码器：使用dropout
"""

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import sys


n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 150  # codings
n_hidden3 = n_hidden1
n_outputs = n_inputs

learning_rate = 0.01

dropout_rate = 0.3
training = tf.placeholder_with_default(False, shape=(), name='training')

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
X_drop = tf.layers.dropout(X, dropout_rate, training=training)

hidden1 = tf.layers.dense(X_drop, n_hidden1, activation=tf.nn.relu,
                          name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, # not shown in the book
                          name="hidden2")                            # not shown
hidden3 = tf.layers.dense(hidden2, n_hidden3, activation=tf.nn.relu, # not shown
                          name="hidden3")                            # not shown
outputs = tf.layers.dense(hidden3, n_outputs, name="outputs")        # not shown

reconstruction_loss = tf.reduce_mean(tf.square(outputs - X)) # MSE

optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(reconstruction_loss)

init = tf.global_variables_initializer()
saver = tf.train.Saver()

n_epochs = 10
batch_size = 150
mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')


with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        n_batches = mnist.train.num_examples // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={
         X: X_batch, training: True})
        loss_train = reconstruction_loss.eval(feed_dict={
         X: X_batch})
        print("\r{}".format(epoch), "Train MSE:", loss_train)
        saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_stacked_denoising_dropout.ckpt")

    • 运行结果：

      img

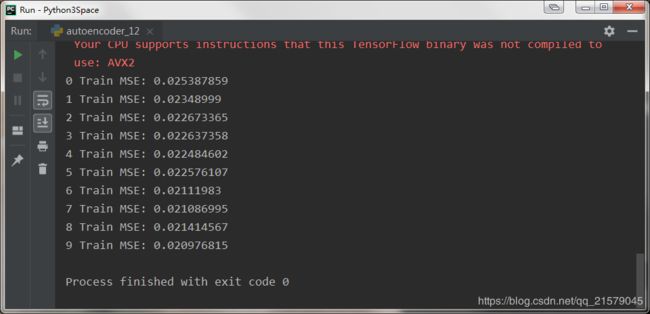
    • 在测试期间没有必要设置is_training为False，因为调用placeholder_with_default()函数时我们设置其为默认值。

  • 稀疏自动编码器

    • 通常良好特征提取的另一种约束是稀疏性：通过向损失函数添加适当的项，自编码器被推动以减少编码层中活动神经元的数量。

    • 一种方法可以简单地将平方误差添加到损失函数中，但实际上更好的方法是使用 Kullback-Leibler 散度（相对熵），其具有比均方误差更强的梯度。它表示2个函数或概率分布的差异性：差异越大则相对熵越大，差异越小则相对熵越小，特别地，若2者相同则熵为0。注意，KL散度的非对称性。

    • 一旦我们已经计算了编码层中每个神经元的稀疏损失，我们就总结这些损失，并将结果添加到损失函数中。 为了控制稀疏损失和重构损失的相对重要性，我们可以用稀疏权重超参数乘以稀疏损失。 如果这个权重太高，模型会紧贴目标稀疏度，但它可能无法正确重建输入，导致模型无用。 相反，如果它太低，模型将大多忽略稀疏目标，它不会学习任何有用的功能。

      • 参考链接：KL散度(相对熵)、交叉熵的解析
      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_13.py
@time: 2019/7/2 10:32
@desc: 稀疏自动编码器
"""
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import sys


n_inputs = 28 * 28
n_hidden1 = 1000  # sparse codings
n_outputs = n_inputs


def kl_divergence(p, q):
    # Kullback Leibler divergence
    return p * tf.log(p / q) + (1 - p) * tf.log((1 - p) / (1 - q))


learning_rate = 0.01
sparsity_target = 0.1
sparsity_weight = 0.2

X = tf.placeholder(tf.float32, shape=[None, n_inputs])            # not shown in the book

hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.sigmoid) # not shown
outputs = tf.layers.dense(hidden1, n_outputs)                     # not shown

hidden1_mean = tf.reduce_mean(hidden1, axis=0)  # batch mean
sparsity_loss = tf.reduce_sum(kl_divergence(sparsity_target, hidden1_mean))
reconstruction_loss = tf.reduce_mean(tf.square(outputs - X)) # MSE
loss = reconstruction_loss + sparsity_weight * sparsity_loss

optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()
saver = tf.train.Saver()

# 训练过程
n_epochs = 100
batch_size = 1000
mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')


with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        n_batches = mnist.train.num_examples // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={
         X: X_batch})
        reconstruction_loss_val, sparsity_loss_val, loss_val = sess.run([reconstruction_loss, sparsity_loss, loss], feed_dict={
         X: X_batch})
        print("\r{}".format(epoch), "Train MSE:", reconstruction_loss_val, "\tSparsity loss:", sparsity_loss_val, "\tTotal loss:", loss_val)
        saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_sparse.ckpt")

    • 运行结果：

      img

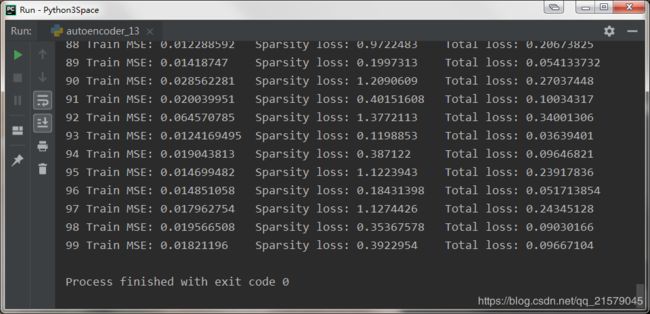
    • 一个重要的细节是，编码器激活度的值是在0-1之间（但是不等于0或1），否则KL散度将返回NaN。一个简单的解决方案是为编码层使用逻辑激活函数：hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.sigmoid)

    • 一个简单的技巧可以加速收敛：不是使用 MSE，我们可以选择一个具有较大梯度的重建损失。 交叉熵通常是一个不错的选择。 要使用它，我们必须对输入进行规范化处理，使它们的取值范围为 0 到 1，并在输出层中使用逻辑激活函数，以便输出也取值为 0 到 1。TensorFlow 的sigmoid_cross_entropy_with_logits()函数负责有效地将logistic（sigmoid）激活函数应用于输出并计算交叉熵。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_14.py
@time: 2019/7/2 10:53
@desc: 稀疏自动编码器：加速收敛方法
"""

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import sys


n_inputs = 28 * 28
n_hidden1 = 1000  # sparse codings
n_outputs = n_inputs


def kl_divergence(p, q):
    # Kullback Leibler divergence
    return p * tf.log(p / q) + (1 - p) * tf.log((1 - p) / (1 - q))


learning_rate = 0.01
sparsity_target = 0.1
sparsity_weight = 0.2

X = tf.placeholder(tf.float32, shape=[None, n_inputs])            # not shown in the book

hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.sigmoid) # not shown
logits = tf.layers.dense(hidden1, n_outputs)                     # not shown
outputs = tf.nn.sigmoid(logits)

hidden1_mean = tf.reduce_mean(hidden1, axis=0)  # batch mean
sparsity_loss = tf.reduce_sum(kl_divergence(sparsity_target, hidden1_mean))

xentropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=X, logits=logits)
reconstruction_loss = tf.reduce_mean(xentropy)
loss = reconstruction_loss + sparsity_weight * sparsity_loss

optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()
saver = tf.train.Saver()

# 训练过程
n_epochs = 100
batch_size = 1000
mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')


with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        n_batches = mnist.train.num_examples // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={
         X: X_batch})
        reconstruction_loss_val, sparsity_loss_val, loss_val = sess.run([reconstruction_loss, sparsity_loss, loss], feed_dict={
         X: X_batch})
        print("\r{}".format(epoch), "Train MSE:", reconstruction_loss_val, "\tSparsity loss:", sparsity_loss_val, "\tTotal loss:", loss_val)
        saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_sparse_speedup.ckpt")

    • 运行结果：

      img

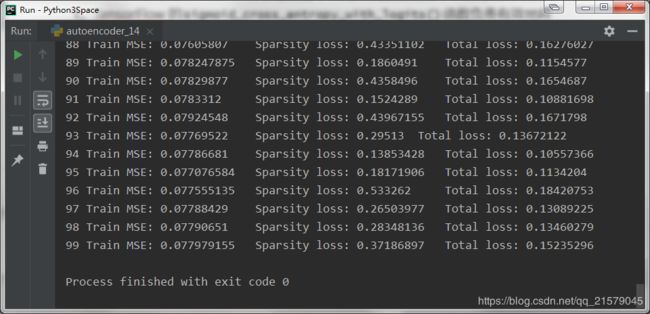
  • 变分自动编码器

    • 它和前面所讨论的所有编码器都不同，特别之处在于：

      • 它们是概率自动编码器，这就意味着即使经过训练，其输出也部分程度上决定于运气（不同于仅在训练期间使用随机性的去噪自动编码器）。

      • 更重要的是，它们是生成自动编码器，意味着它们可以生成看起来像是从训练样本采样的新实例。

      • 参考文献： 变分自编码器（一）：原来是这么一回事

      • VAE的名字中“变分”，是因为它的推导过程用到了KL散度及其性质。

        #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_15.py
@time: 2019/7/3 9:42
@desc: 变分自动编码器
"""

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import sys
from functools import partial


n_inputs = 28 * 28
n_hidden1 = 500
n_hidden2 = 500
n_hidden3 = 20  # codings
n_hidden4 = n_hidden2
n_hidden5 = n_hidden1
n_outputs = n_inputs
learning_rate = 0.001

initializer = tf.contrib.layers.variance_scaling_initializer()

my_dense_layer = partial(
    tf.layers.dense,
    activation=tf.nn.elu,
    kernel_initializer=initializer)

X = tf.placeholder(tf.float32, [None, n_inputs])
hidden1 = my_dense_layer(X, n_hidden1)
hidden2 = my_dense_layer(hidden1, n_hidden2)
hidden3_mean = my_dense_layer(hidden2, n_hidden3, activation=None)
hidden3_sigma = my_dense_layer(hidden2, n_hidden3, activation=None)
hidden3_gamma = my_dense_layer(hidden2, n_hidden3, activation=None)
noise = tf.random_normal(tf.shape(hidden3_sigma), dtype=tf.float32)
hidden3 = hidden3_mean + hidden3_sigma * noise
hidden4 = my_dense_layer(hidden3, n_hidden4)
hidden5 = my_dense_layer(hidden4, n_hidden5)
logits = my_dense_layer(hidden5, n_outputs, activation=None)
outputs = tf.sigmoid(logits)

xentropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=X, logits=logits)
reconstruction_loss = tf.reduce_sum(xentropy)

eps = 1e-10 # smoothing term to avoid computing log(0) which is NaN
latent_loss = 0.5 * tf.reduce_sum(
    tf.square(hidden3_sigma) + tf.square(hidden3_mean)
    - 1 - tf.log(eps + tf.square(hidden3_sigma)))

# 一个常见的变体
# latent_loss = 0.5 * tf.reduce_sum(
#     tf.exp(hidden3_gamma) + tf.square(hidden3_mean) - 1 - hidden3_gamma)
loss = reconstruction_loss + latent_loss

optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()
saver = tf.train.Saver()

n_epochs = 50
batch_size = 150
mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')


with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        n_batches = mnist.train.num_examples // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={
           X: X_batch})
        loss_val, reconstruction_loss_val, latent_loss_val = sess.run([loss, reconstruction_loss, latent_loss], feed_dict={
           X: X_batch})
        print("\r{}".format(epoch), "Train total loss:", loss_val, "\tReconstruction loss:", reconstruction_loss_val, "\tLatent loss:", latent_loss_val)
        saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_variational.ckpt")

      • 运行结果

        img

  • 生成数字

    • 用上述变分自动编码器生成一些看起来像手写数字的图片。我们需要做的是训练模型，然后从高斯分布中随机采样编码并对其进行解码。

      #!/usr/bin/env python
# -*- coding: UTF-8 -*-
# coding=utf-8 

"""
@author: Li Tian
@contact: [email protected]
@software: pycharm
@file: autoencoder_16.py
@time: 2019/7/3 10:12
@desc: 生成数字
"""

import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import sys
from functools import partial
import matplotlib.pyplot as plt


n_inputs = 28 * 28
n_hidden1 = 500
n_hidden2 = 500
n_hidden3 = 20  # codings
n_hidden4 = n_hidden2
n_hidden5 = n_hidden1
n_outputs = n_inputs
learning_rate = 0.001

initializer = tf.contrib.layers.variance_scaling_initializer()

my_dense_layer = partial(
    tf.layers.dense,
    activation=tf.nn.elu,
    kernel_initializer=initializer)

X = tf.placeholder(tf.float32, [None, n_inputs])
hidden1 = my_dense_layer(X, n_hidden1)
hidden2 = my_dense_layer(hidden1, n_hidden2)
hidden3_mean = my_dense_layer(hidden2, n_hidden3, activation=None)
hidden3_sigma = my_dense_layer(hidden2, n_hidden3, activation=None)
hidden3_gamma = my_dense_layer(hidden2, n_hidden3, activation=None)
noise = tf.random_normal(tf.shape(hidden3_sigma), dtype=tf.float32)
hidden3 = hidden3_mean + hidden3_sigma * noise
hidden4 = my_dense_layer(hidden3, n_hidden4)
hidden5 = my_dense_layer(hidden4, n_hidden5)
logits = my_dense_layer(hidden5, n_outputs, activation=None)
outputs = tf.sigmoid(logits)

xentropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=X, logits=logits)
reconstruction_loss = tf.reduce_sum(xentropy)

eps = 1e-10 # smoothing term to avoid computing log(0) which is NaN
latent_loss = 0.5 * tf.reduce_sum(
    tf.square(hidden3_sigma) + tf.square(hidden3_mean)
    - 1 - tf.log(eps + tf.square(hidden3_sigma)))

# 一个常见的变体
# latent_loss = 0.5 * tf.reduce_sum(
#     tf.exp(hidden3_gamma) + tf.square(hidden3_mean) - 1 - hidden3_gamma)
loss = reconstruction_loss + latent_loss

optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()
saver = tf.train.Saver()


n_digits = 60
n_epochs = 50
batch_size = 150
mnist = input_data.read_data_sets('D:/Python3Space/BookStudy/book2/MNIST_data/')


with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        n_batches = mnist.train.num_examples // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")  # not shown in the book
            sys.stdout.flush()  # not shown
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={
         X: X_batch})
        loss_val, reconstruction_loss_val, latent_loss_val = sess.run([loss, reconstruction_loss, latent_loss],
                                                                      feed_dict={
         X: X_batch})  # not shown
        print("\r{}".format(epoch), "Train total loss:", loss_val, "\tReconstruction loss:", reconstruction_loss_val,
              "\tLatent loss:", latent_loss_val)  # not shown
        saver.save(sess, "D:/Python3Space/BookStudy/book4/model/my_model_variational2.ckpt")  # not shown

    codings_rnd = np.random.normal(size=[n_digits, n_hidden3])
    outputs_val = outputs.eval(feed_dict={
         hidden3: codings_rnd})


def plot_image(image, shape=[28, 28]):
    plt.imshow(image.reshape(shape), cmap="Greys", interpolation="nearest")
    plt.axis("off")


def plot_multiple_images(images, n_rows, n_cols, pad=2):
    images = images - images.min()  # make the minimum == 0, so the padding looks white
    w,h = images.shape[1:]
    image = np.zeros(((w+pad)*n_rows+pad, (h+pad)*n_cols+pad))
    for y in range(n_rows):
        for x in range(n_cols):
            image[(y*(h+pad)+pad):(y*(h+pad)+pad+h),(x*(w+pad)+pad):(x*(w+pad)+pad+w)] = images[y*n_cols+x]
    plt.imshow(image, cmap="Greys", interpolation="nearest")
    plt.axis("off")


plt.figure(figsize=(8,50)) # not shown in the book
for iteration in range(n_digits):
    plt.subplot(n_digits, 10, iteration + 1)
    plot_image(outputs_val[iteration])
plt.show()

n_rows = 6
n_cols = 10
plot_multiple_images(outputs_val.reshape(-1, 28, 28), n_rows, n_cols)
plt.show()

    • 运行结果：

      img

  • 其他自动编码器

    • 收缩自动编码器（CAE）：该自动编码器在训练期间加入限制，使得关于输入编码的衍生物比较小。换句话说，相似的输入会得到相似的编码。
    • 栈式卷积自动编码器：该自动编码器通过卷积层重构图像来学习提取视觉特征。
    • 随机生成网络（GSN）：去噪自动编码器的推广，增加了生成数据的能力。
    • 获胜者（WTA）自动编码器：训练期间，在计算了编码层所有神经元的激活度之后，只保留训练批次中前k%的激活度，其余都置为0。自然的，这将导致稀疏编码。此外，类似的WTA方法可以用于产生稀疏卷积自动编码器。
    • 对抗自动编码器：一个网络被训练来重现输入，同时另一个网络被训练来找到不能正确重建第一个网络的输入。这促使第一个自动编码器学习鲁棒编码。

  • 部分课后题的摘抄

    1. 自动编码器的主要任务是什么？

      • 特征提取
      • 无监督的预训练
      • 降低维度
      • 生成模型
      • 异常检测（自动编码器在重建异常点时通常表现得不太好）

    2. 加入想训练一个分类器，而且有大量未训练的数据，但是只有几千个已经标记的实例。自动编码器可以如何帮助你？你会如何实现？

      首先可以在完整的数据集（已标记和未标记）上训练一个深度自动编码器，然后重用其下半部分作为分类器（即重用上半部分作为编码层）并使用已标记的数据训练分类器。如果已标记的数据集比较小，你可能希望在训练分类器时冻结复用层。

    3. 如果自动编码器可以完美的重现输入，它就是一个好的自动编码器吗？如何评估自动编码器的性能？

      完美的重建并不能保证自动编码器学习到有用的东西。然而，如果产生非常差的重建，它几乎必然是一个糟糕的自动编码器。

      为了评估编码器的性能，一种方法是测量重建损失（例如，计算MSE，用输入的均方值减去输入）。同样，重建损失高意味着这是一个不好的编码器，但是重建损失低并不能保证这是一个好的自动编码器。你应该根据它的用途来评估自动编码器。例如，如果它用于无监督分类器的预训练，同样应该评估分类器的性能。

    4. 什么是不完整和完整自动编码器？不啊完整自动编码器的主要风险是什么？完整的意义是什么？

      不完整的自动编码器是**编码层比输入和输出层小**的自动编码器。如果比其大，那就是一个完整的自动编码器。一个过度不完整的自动编码器的主要风险是：不能重建其输入。完整的自动编码器的主要风险是：它可能只是将输入复制到输出，不学习任何有用的特征。

    5. 如何在栈式自动编码器上绑定权重？为什么要这样做？

      要将自动编码器的权重与其相应的解码层相关联，你可以简单的使得解码权重等于编码权重的转置。这将使得模型参数数量减少一半，通常使得训练在数据较少时快速收敛，减少过度拟合的危险。

    6. 栈式自动编码器低层学习可视化特征的常用技术是什么？高层又是什么？

      为了可视化栈式自动编码器低层学习到的特征，一个常用的技术是通过将每个权重向量重建为输入图像的大小来绘制每个神经元的权重（例如，对MNIST，将权重向量形状[784]重建为[28, 28]）。为了可视化高层学习到的特征，一种技术是显示最能激活每个神经元的训练实例。

    7. 什么是生成模型？你能列举一种生成自动编码器吗？

      生成模型是一种可以随机生成类似于训练实例的输出的模型。

      例如，一旦在MNIST数据集上训练成功，生成模型就可以用于随机生成逼真的数字图像。输出分布大致和训练数据类似。例如，因为MNIST包含了每个数字的多个图像，生成模型可以输出与每个数字大致数量相同的图像。有些生成模型可以进行参数化，例如，生成某种类型的输出。生成自动编码器的一个例子是变分自动编码器。

16. 强化学习

  • 如代码所示

我的CSDN：https://blog.csdn.net/qq_21579045

我的博客园：https://www.cnblogs.com/lyjun/

我的Github：https://github.com/TinyHandsome

纸上得来终觉浅，绝知此事要躬行~

欢迎大家过来OB~

by 李英俊小朋友

你可能感兴趣的:(机器学习实战基于S和T,tensorflow,sklearn,机器学习,实战,学习笔记)

  • 情绪觉察日记第37天 露露_e800
    今天是家庭关系规划师的第二阶最后一天，慧萍老师帮我做了个案，帮我处理了埋在心底好多年的一份恐惧，并给了我深深的力量！这几天出来学习，爸妈过来婆家帮我带小孩，妈妈出于爱帮我收拾东西，并跟我先生和婆婆产生矛盾，妈妈觉得他们没有照顾好我…。今晚回家见到妈妈，我很欣赏她并赞扬她，妈妈说今晚要跟我睡我说好，当我们俩躺在床上准备睡觉的时候，我握着妈妈的手对她说:妈妈这几天辛苦你了，你看你多利害把我们的家收拾得
  • 芦花鞋一四 许叶晗
    又是在一个寒冷的夏日里，青铜和葵花决定今天一起去卖芦花鞋，奶奶亲手给他们做了一碗热乎乎的粥对他们说:“就靠你们两挣生活费了这碗粥赶紧趁热喝了吧！”于是青铜和葵花喝完了奶奶给她们做的粥，就准备去镇上卖卢花鞋，这回青铜和葵花穿着新的芦花鞋来到了镇上。青铜这回看到了很多人都在卖，用手势表达对葵花说:“这回有好多人在抢我们生意呢！我们必须得吆喝起来。”葵花点了点头。可是谁知他们也大声的叫，卖芦花喽！卖芦花
  • 关于沟通这件事，项目经理不需要每次都面对面进行 流程大师兄
    很多项目经理都会遇到这样的问题，项目中由于事情太多，根本没有足够的时间去召开会议，那在这种情况下如何去有效地管理项目中的利益相关者？当然，不建议电子邮件也不需要开会的话，建议可以采取下面几种方式来形成有效的沟通，这几种方式可以帮助你努力的通过各种办法来保持和各方面的联系。项目经理首先要问自己几个问题，项目中哪些利益相关者是必须要进行沟通的？可以列出项目中所有的利益相关者清单，同时也整理出项目中哪些
  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • android系统selinux中添加新属性property 辉色投像
    1.定位/android/system/sepolicy/private/property_contexts声明属性开头：persist.charge声明属性类型：u:object_r:system_prop:s0图12.定位到android/system/sepolicy/public/domain.te删除neverallow{domain-init}default_prop:property
  • 【iOS】MVC设计模式 Magnetic_h iosmvc设计模式objective-c学习ui
    MVC前言如何设计一个程序的结构，这是一门专门的学问，叫做"架构模式"（architecturalpattern），属于编程的方法论。MVC模式就是架构模式的一种。它是Apple官方推荐的App开发架构，也是一般开发者最先遇到、最经典的架构。MVC各层controller层Controller/ViewController/VC（控制器）负责协调Model和View，处理大部分逻辑它将数据从Mod
  • 一百九十四章. 自相矛盾 巨木擎天
    唉！就这么一夜，林子感觉就像过了很多天似的，先是回了阳间家里，遇到了那么多不可思议的事情儿。特别是小伙伴们，第二次与自己见面时，僵硬的表情和恐怖的气氛，让自己如坐针毡，打从心眼里难受！还有东子，他现在还好吗？有没有被人欺负？护城河里的小鱼小虾们，还都在吗？水不会真的干枯了吧？那对相亲相爱漂亮的太平鸟儿，还好吧！春天了，到了做窝、下蛋、喂养小鸟宝宝的时候了，希望它们都能够平安啊！虽然没有看见家人，也
  • UI学习——cell的复用和自定义cell Magnetic_h ui学习
    目录cell的复用手动（非注册）自动（注册）自定义cellcell的复用在iOS开发中，单元格复用是一种提高表格（UITableView）和集合视图（UICollectionView）滚动性能的技术。当一个UITableViewCell或UICollectionViewCell首次需要显示时，如果没有可复用的单元格，则视图会创建一个新的单元格。一旦这个单元格滚动出屏幕，它就不会被销毁。相反，它被添
  • element实现动态路由+面包屑 软件技术NINI vue案例vue.js前端
    el-breadcrumb是ElementUI组件库中的一个面包屑导航组件，它用于显示当前页面的路径，帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中，如果你已经安装了ElementUI，就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例：安装ElementUI（如果你还没有安装的话）:你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
  • 地推话术，如何应对地推过程中家长的拒绝 校师学
    相信校长们在做地推的时候经常遇到这种情况：市场专员反馈家长不接单，咨询师反馈难以邀约这些家长上门，校区地推疲软，招生难。为什么？仅从地推层面分析，一方面因为家长受到的信息轰炸越来越多，对信息越来越“免疫”；而另一方面地推人员的专业能力和营销话术没有提高，无法应对家长的拒绝，对有意向的家长也不知如何跟进，眼睁睁看着家长走远；对于家长的疑问，更不知道如何有技巧地回答，机会白白流失。由于回答没技巧和专业
  • 谢谢你们，爱你们！ 鹿游儿
    昨天家人去泡温泉，二个孩子也带着去，出发前一晚，匆匆下班，赶回家和孩子一起收拾。饭后，我拿出笔和本子（上次去澳门时做手帐的本子）写下了1\2\3\4\5\6\7\8\9,让后让小壹去思考，带什么出发去旅游呢？她在对应的数字旁边画上了，泳衣、泳圈、肖恩、内衣内裤、tapuy、拖鞋……画完后，就让她自己对着这个本子，将要带的，一一带上，没想到这次带的书还是这本《便便工厂》(晚上姑婆发照片过来，妹妹累得
  • C语言如何定义宏函数？ 小九格物 c语言
    在C语言中，宏函数是通过预处理器定义的，它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为，但它们不是真正的函数，因为它们在编译时不会进行类型检查，也不会分配存储空间。宏函数的定义通常使用#define指令，后面跟着宏的名称和参数列表，以及宏展开后的代码。宏函数的定义方式：1.基本宏函数：这是最简单的宏函数形式，它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
  • 微服务下功能权限与数据权限的设计与实现 nbsaas-boot 微服务java架构
    在微服务架构下，系统的功能权限和数据权限控制显得尤为重要。随着系统规模的扩大和微服务数量的增加，如何保证不同用户和服务之间的访问权限准确、细粒度地控制，成为设计安全策略的关键。本文将讨论如何在微服务体系中设计和实现功能权限与数据权限控制。1.功能权限与数据权限的定义功能权限：指用户或系统角色对特定功能的访问权限。通常是某个用户角色能否执行某个操作，比如查看订单、创建订单、修改用户资料等。数据权限：
  • 理解Gunicorn：Python WSGI服务器的基石 范范0825 ipythonlinux运维
    理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
  • 2021年12月19日，春蕾教育集团团建活动感受——黄晓丹 黄错错加油
    感受:1.从陌生到熟悉的过程。游戏环节让我们在轻松的氛围中得到了锻炼，也增长了不少知识。2.游戏过程中，我们贡献的是个人力量，展现的是团队的力量。它磨合的往往不止是工作的熟悉，更是观念上契合度的贴近。3.这和工作是一样的道理。在各自的岗位上，每个人摆正自己的位置、各司其职充分发挥才能，并团结一致劲往一处使，才能实现最大的成功。新知:1.团队精神需要不断地创新。过去，人们把创新看作是冒风险，现在人们
  • Cell Insight | 单细胞测序技术又一新发现，可用于HIV-1和Mtb共感染个体诊断 尐尐呅
    结核病是艾滋病合并其他疾病中导致患者死亡的主要原因。其中结核病由结核分枝杆菌（Mycobacteriumtuberculosis,Mtb）感染引起，获得性免疫缺陷综合症（艾滋病）由人免疫缺陷病毒（Humanimmunodeficiencyvirustype1,HIV-1）感染引起。国家感染性疾病临床医学研究中心/深圳市第三人民医院张国良团队携手深圳华大生命科学研究院吴靓团队，共同研究得出单细胞测序
  • c++ 的iostream 和 c++的stdio的区别和联系 黄卷青灯77 c++算法开发语言iostreamstdio
    在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
  • 《投行人生》读书笔记 小蘑菇的树洞
    《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
  • 如何在 Fork 的 GitHub 项目中保留自己的修改并同步上游更新？github_fork_update iBaoxing github
    如何在Fork的GitHub项目中保留自己的修改并同步上游更新？在GitHub上Fork了一个项目后，你可能会对项目进行一些修改，同时原作者也在不断更新。如果想要在保留自己修改的基础上，同步原作者的最新更新，很多人会不知所措。本文将详细讲解如何在不丢失自己改动的情况下，将上游仓库的更新合并到自己的仓库中。问题描述假设你在GitHub上Fork了一个项目，并基于该项目做了一些修改，随后你发现原作者对
  • Linux下QT开发的动态库界面弹出操作（SDL2） 13jjyao QT类qt开发语言sdl2linux
    需求：操作系统为linux，开发框架为qt，做成需带界面的qt动态库，调用方为java等非qt程序难点：调用方为java等非qt程序，也就是说调用方肯定不带QApplication::exec()，缺少了这个，QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出)；这与qt调用本身qt库是有本质的区别的思路：1.调用方缺QApplication::exec()，那么我们在接口
  • 绘本讲师训练营【24期】8/21阅读原创《独生小孩》 1784e22615e0
    24016-孟娟《独生小孩》图片发自App今天我想分享一个蛮特别的绘本，讲的是一个特殊的群体，我也是属于这个群体，80后的独生小孩。这是一本中国绘本，作者郭婧，也是一个80厚。全书一百多页，均为铅笔绘制，虽然为黑白色调，但并不显得沉闷。全书没有文字，犹如“默片”，但并不影响读者对该作品的理解，反而显得神秘，梦幻，給读者留下想象的空间。作者在前蝴蝶页这样写到：“我更希望父母和孩子一起分享这本书，使他
  • 店群合一模式下的社区团购新发展——结合链动 2+1 模式、AI 智能名片与 S2B2C 商城小程序源码 说私域 人工智能小程序
    摘要：本文探讨了店群合一的社区团购平台在当今商业环境中的重要性和优势。通过分析店群合一模式如何将互联网社群与线下终端紧密结合，阐述了链动2+1模式、AI智能名片和S2B2C商城小程序源码在这一模式中的应用价值。这些创新元素的结合为社区团购带来了新的机遇，提升了用户信任感、拓展了营销渠道，并实现了线上线下的完美融合。一、引言随着互联网技术的不断发展，社区团购作为一种新兴的商业模式，在满足消费者日常需
  • 消息中间件有哪些常见类型 xmh-sxh-1314 java
    消息中间件根据其设计理念和用途，可以大致分为以下几种常见类型：点对点消息队列（Point-to-PointMessagingQueues）：在这种模型中，消息被发送到特定的队列中，消费者从队列中取出并处理消息。队列中的消息只能被一个消费者消费，消费后即被删除。常见的实现包括IBM的MQSeries、RabbitMQ的部分使用场景等。适用于任务分发、负载均衡等场景。发布/订阅消息模型（Pub/Sub
  • ArcGIS栅格计算器常见公式（赋值、0和空值的转换、补充栅格空值） 研学随笔 arcgis经验分享
    我们在使用ArcGIS时通常经常用到栅格计算器，今天主要给大家介绍我日常中经常用到的几个公式，供大家参考学习。将特定值（-9999）赋值为0，例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值（如0）Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值，其他保留原值SetNull("raster"==
  • 水平垂直居中的几种方法（总结） LJ小番茄 CSS_玄学语言htmljavascript前端csscss3
    1.使用flexbox的justify-content和align-items.parent{display:flex;justify-content:center;/*水平居中*/align-items:center;/*垂直居中*/height:100vh;/*需要指定高度*/}2.使用grid的place-items:center.parent{display:grid;place-item
  • 【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数 广龙宇 一起学Rust#Rust设计模式rust设计模式开发语言
    提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言，它的所有特性，使其独一无二。因此，学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此，本系列文章的结构也与此书的结构相同（后续可能会调成结构），基本上分为三个部分
  • 本周第二次约练 2cfbdfe28a51
    中原焦点团队中24初26刘霞2021.12.3约练161次，分享第368天当事人虽然是带着问题来的，但是咨询过程中发现，她是经过自己不断地调整和努力才走到现在的，看到当事人的不容易，找到例外，发现资源，力量感也就随之而来。增强画面感，或者说重温，会给当事人带来更深刻的感受。
  • 放下是一段成长的修行 小莳玥
    人来到这个世界上，只有两件事：生和死。一件事已经做完了，另一件你还急什么呢?是人，都有七情六欲。是心，都有喜怒哀乐，这些再正常不过了。别总抱怨自己活得累，过得辛苦。永远记住：舒坦是留给死人的。苦，才是生活；累，才是工作；变，才是命运；忍，才是历练；容，才是智慧；静，才是修养；舍，才会得到；做，才会拥有。人生，活得太清楚，才是最大的不明白。有些事，看得很清，却说不清；有些人，了解很深，却猜不透；有些
  • 回溯 Leetcode 332 重新安排行程 mmaerd Leetcode刷题学习记录leetcode算法职场和发展
    重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets，其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从JFK开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。例如，行程[“JFK”,“LGA”]与[“JFK”,“LGB
  • Python数据分析与可视化实战指南 William数据分析 pythonpython数据
    在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
  • github中多个平台共存 jackyrong github
    在个人电脑上，如何分别链接比如oschina,github等库呢，一般教程之列的，默认 ssh链接一个托管的而已，下面讲解如何放两个文件 1） 设置用户名和邮件地址 $ git config --global user.name "xx" $ git config --global user.email "[email protected]"
  • ip地址与整数的相互转换(javascript) alxw4616 JavaScript
    //IP转成整型 function ip2int(ip){ var num = 0; ip = ip.split("."); num = Number(ip[0]) * 256 * 256 * 256 + Number(ip[1]) * 256 * 256 + Number(ip[2]) * 256 + Number(ip[3]); n
  • 读书笔记-jquey+数据库+css chengxuyuancsdn htmljqueryoracle
    1、grouping ,group by rollup, GROUP BY GROUPING SETS区别 2、$("#totalTable tbody>tr td:nth-child(" + i + ")").css({"width":tdWidth, "margin":"0px", &q
  • javaSE javaEE javaME == API下载 Array_06 java
    oracle下载各种API文档： http://www.oracle.com/technetwork/java/embedded/javame/embed-me/documentation/javame-embedded-apis-2181154.html JavaSE文档： http://docs.oracle.com/javase/8/docs/api/ JavaEE文档： ht
  • shiro入门学习 cugfy javaWeb框架
    声明本文只适合初学者，本人也是刚接触而已，经过一段时间的研究小有收获，特来分享下希望和大家互相交流学习。 首先配置我们的web.xml代码如下，固定格式，记死就成 <filter>         <filter-name>shiroFilter</filter-name> &nbs
  • Array添加删除方法 357029540 js
         刚才做项目前台删除数组的固定下标值时，删除得不是很完整，所以在网上查了下，发现一个不错的方法，也提供给需要的同学。 //给数组添加删除             Array.prototype.del = function(n){
  • navigation bar 更改颜色 张亚雄 IO
    今天郁闷了一下午，就因为objective-c默认语言是英文，我写的中文全是一些乱七八糟的样子，到不是乱码，但是，前两个自字是粗体，后两个字正常体，这可郁闷死我了，问了问大牛，人家告诉我说更改一下字体就好啦，比如改成黑体，哇塞，茅塞顿开。       翻书看，发现，书上有介绍怎么更改表格中文字字体的，代码如下    
  • unicode转换成中文 adminjun unicode编码转换
      在Java程序中总会出现\u6b22\u8fce\u63d0\u4ea4\u5fae\u535a\u641c\u7d22\u4f7f\u7528\u53cd\u9988\uff0c\u8bf7\u76f4\u63a5这个的字符，这是unicode编码，使用时有时候不会自动转换成中文就需要自己转换了使用下面的方法转换一下即可。 /** * unicode 转换成 中文
  • 一站式 Java Web 框架 firefly aijuans Java Web
    Firefly是一个高性能一站式Web框架。 涵盖了web开发的主要技术栈。 包含Template engine、IOC、MVC framework、HTTP Server、Common tools、Log、Json parser等模块。 firefly-2.0_07修复了模版压缩对javascript单行注释的影响，并新增了自定义错误页面功能。 更新日志： 增加自定义系统错误页面功能
  • 设计模式——单例模式 ayaoxinchao 设计模式
    定义          Java中单例模式定义：“一个类有且仅有一个实例，并且自行实例化向整个系统提供。”   分析          从定义中可以看出单例的要点有三个：一是某个类只能有一个实例；二是必须自行创建这个实例；三是必须自行向系统提供这个实例。   &nb
  • Javascript 多浏览器兼容性问题及解决方案 BigBird2012 JavaScript
    不论是网站应用还是学习js,大家很注重ie与firefox等浏览器的兼容性问题，毕竟这两中浏览器是占了绝大多数。 一、document.formName.item(”itemName”) 问题 问题说明：IE下，可以使用 document.formName.item(”itemName”) 或 document.formName.elements ["elementName&quo
  • JUnit-4.11使用报java.lang.NoClassDefFoundError: org/hamcrest/SelfDescribing错误 bijian1013 junit4.11单元测试
            下载了最新的JUnit版本，是4.11，结果尝试使用发现总是报java.lang.NoClassDefFoundError: org/hamcrest/SelfDescribing这样的错误，上网查了一下，一般的解决方案是，换一个低一点的版本就好了。还有人说，是缺少hamcrest的包。去官网看了一下，如下发现：    
  • [Zookeeper学习笔记之二]Zookeeper部署脚本 bit1129 zookeeper
    Zookeeper伪分布式安装脚本(此脚本在一台机器上创建Zookeeper三个进程，即创建具有三个节点的Zookeeper集群。这个脚本和zookeeper的tar包放在同一个目录下，脚本中指定的名字是zookeeper的3.4.6版本，需要根据实际情况修改)：   #!/bin/bash #!!!Change the name!!! #The zookeepe
  • 【Spark八十】Spark RDD API二 bit1129 spark
    coGroup package spark.examples.rddapi import org.apache.spark.{SparkConf, SparkContext} import org.apache.spark.SparkContext._ object CoGroupTest_05 { def main(args: Array[String]) { v
  • Linux中编译apache服务器modules文件夹缺少模块(.so)的问题 ronin47 modules
    在modules目录中只有httpd.exp，那些so文件呢？ 我尝试在fedora core 3中安装apache 2. 当我解压了apache 2.0.54后使用configure工具并且加入了 --enable-so 或者 --enable-modules=so (两个我都试过了) 去make并且make install了。我希望在/apache2/modules/目录里有各种模块，
  • Java基础-克隆 BrokenDreams java基础
            Java中怎么拷贝一个对象呢？可以通过调用这个对象类型的构造器构造一个新对象，然后将要拷贝对象的属性设置到新对象里面。Java中也有另一种不通过构造器来拷贝对象的方式，这种方式称为 克隆。         Java提供了java.lang.
  • 读《研磨设计模式》-代码笔记-适配器模式-Adapter bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ package design.pattern; /* * 适配器模式解决的主要问题是，现有的方法接口与客户要求的方法接口不一致 * 可以这样想，我们要写这样一个类（Adapter）: * 1.这个类要符合客户的要求 ---> 那显然要
  • HDR图像PS教程集锦&心得 cherishLC PS
    HDR是指高动态范围的图像，主要原理为提高图像的局部对比度。 软件有photomatix和nik hdr efex。 一、教程 叶明在知乎上的回答： http://www.zhihu.com/question/27418267/answer/37317792 大意是修完后直方图最好是等值直方图，方法是HDR软件调一遍，再结合不透明度和蒙版细调。 二、心得 1、去除阴影部分的
  • maven-3.3.3 mvn archetype 列表 crabdave ArcheType
    maven-3.3.3 mvn archetype 列表 可以参考最新的：http://repo1.maven.org/maven2/archetype-catalog.xml   [INFO] Scanning for projects... [INFO]                
  • linux shell 中文件编码查看及转换方法 daizj shell中文乱码vim文件编码
    一、查看文件编码。     在打开文件的时候输入:set fileencoding     即可显示文件编码格式。 二、文件编码转换     1、在Vim中直接进行转换文件编码,比如将一个文件转换成utf-8格式       &
  • MySQL--binlog日志恢复数据 dcj3sjt126com binlog
    恢复数据的重要命令如下 mysql> flush logs; 默认的日志是mysql-bin.000001，现在刷新了重新开启一个就多了一个mysql-bin.000002                  
  • 数据库中数据表数据迁移方法 dcj3sjt126com sql
    刚开始想想好像挺麻烦的，后来找到一种方法了，就SQL中的 INSERT 语句，不过内容是现从另外的表中查出来的，其实就是 MySQL中INSERT INTO SELECT的使用   下面看看如何使用   语法：MySQL中INSERT INTO SELECT的使用 1. 语法介绍       有三张表a、b、c，现在需要从表b
  • Java反转字符串 dyy_gusi java反转字符串
           前几天看见一篇文章，说使用Java能用几种方式反转一个字符串。首先要明白什么叫反转字符串，就是将一个字符串到过来啦，比如"倒过来念的是小狗"反转过来就是”狗小是的念来过倒“。接下来就把自己能想到的所有方式记录下来了。 1、第一个念头就是直接使用String类的反转方法，对不起，这样是不行的，因为Stri
  • UI设计中我们为什么需要设计动效 gcq511120594 UIlinux
    随着国际大品牌苹果和谷歌的引领，最近越来越多的国内公司开始关注动效设计了，越来越多的团队已经意识到动效在产品用户体验中的重要性了，更多的UI设计师们也开始投身动效设计领域。 但是说到底，我们到底为什么需要动效设计？或者说我们到底需要什么样的动效？做动效设计也有段时间了，于是尝试用一些案例，从产品本身出发来说说我所思考的动效设计。 一、加强体验舒适度 嗯，就是让用户更加爽更加爽的用
  • JBOSS服务部署端口冲突问题 HogwartsRow java应用服务器jbossserverEJB3
    服务端口冲突问题的解决方法，一般修改如下三个文件中的部分端口就可以了。   1、jboss5/server/default/conf/bindingservice.beans/META-INF/bindings-jboss-beans.xml   2、./server/default/deploy/jbossweb.sar/server.xml   3、.
  • 第三章 Redis/SSDB+Twemproxy安装与使用 jinnianshilongnian ssdbreidstwemproxy
    目前对于互联网公司不使用Redis的很少，Redis不仅仅可以作为key-value缓存，而且提供了丰富的数据结果如set、list、map等，可以实现很多复杂的功能；但是Redis本身主要用作内存缓存，不适合做持久化存储，因此目前有如SSDB、ARDB等，还有如京东的JIMDB，它们都支持Redis协议，可以支持Redis客户端直接访问；而这些持久化存储大多数使用了如LevelDB、RocksD
  • ZooKeeper原理及使用 liyonghui160com
               ZooKeeper是Hadoop Ecosystem中非常重要的组件，它的主要功能是为分布式系统提供一致性协调(Coordination)服务，与之对应的Google的类似服务叫Chubby。今天这篇文章分为三个部分来介绍ZooKeeper，第一部分介绍ZooKeeper的基本原理，第二部分介绍ZooKeeper
  • 程序员解决问题的60个策略 pda158 框架工作单元测试
    根本的指导方针 1. 首先写代码的时候最好不要有缺陷。最好的修复方法就是让 bug 胎死腹中。 良好的单元测试 强制数据库约束 使用输入验证框架 避免未实现的“else”条件 在应用到主程序之前知道如何在孤立的情况下使用   日志 2. print 语句。往往额外输出个一两行将有助于隔离问题。 3. 切换至详细的日志记录。详细的日
  • Create the Google Play Account sillycat Google
    Create the Google Play Account Having a Google account, pay 25$, then you get your google developer account. References: http://developer.android.com/distribute/googleplay/start.html https://p
  • JSP三大指令 vikingwei jsp
    JSP三大指令   一个jsp页面中，可以有0~N个指令的定义！ 1. page --> 最复杂：<%@page language="java" info="xxx"...%>   * pageEncoding和contentType：     > pageEncoding：它
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他