逻辑斯谛回归模型处理Kaggle泰坦尼克号之灾

0 前言

【声明】本文主要是实现一遍寒小阳相关博客的代码，由于原文已经有一定历史，由于版本更新，有些代码不再适用，本文在此做了修改；另外本文还对其中一些知识点做了解释和拓展。

【原文相关信息】
作者： 寒小阳
时间：2015年11月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/49797143

【背景】今天我们处理的问题是kaggle里面非常著名的泰坦尼克号之灾。
    泰坦尼克号的沉没是历史上最臭名昭著的沉船之一。1912年4月15日，泰坦尼克号从英国南安普敦(Southampton)港出发，途经法国瑟堡-奥克特维尔(Cherbourg-Octeville)以及回爱尔兰 昆士敦(Queenstown)，计划中的答目的地为美国纽约(New York)，开始了这艘“梦幻客轮”的处女航。被广泛认为是“永不沉没”的皇家邮轮“泰坦尼克号”在处女航中撞上一座冰山后沉没。不幸的是，船上没有足够的救生艇，导致2224名乘客和船员中有1502人死亡。虽然在生存中有一些运气因素，但似乎有些群体的人比其他人更有可能生存下来。在这个挑战中，我们要求你建立一个预测模型来回答以下问题:哪种人更有可能存活?使用乘客数据(如姓名、年龄、性别、社会经济阶层等)。
    数据在此，翻我牌子

【分析】

• 这就是那个大家都熟悉的『Jack and Rose』的故事，豪华游艇倒了，大家都惊恐逃生，可是救生艇的数量有限，无法人人都有，副船长发话了『lady and kid first！』，所以是否获救其实并非随机，而是基于一些背景有rank先后的。
• 训练和测试数据是一些乘客的个人信息以及存活状况，要尝试根据它生成合适的模型并预测其他人的存活状况。
• 这是一个二分类问题，我们可以思考使用常见的二分类模型处理，本文主要用Logistic Regression。

【观点】
『解决一个问题的方法和思路不止一种』
『没有所谓的机器学习算法优劣，也没有绝对高性能的机器学习算法，只有在特定的场景、数据和特征下更合适的机器学习算法。』

【经验】

• 印象中Andrew Ng老师似乎在coursera上说过，应用机器学习，千万不要一上来就试图做到完美，先撸一个baseline的model出来，再进行后续的分析步骤，一步步提高，所谓后续步骤可能包括『分析model现在的状态(欠/过拟合)，分析我们使用的feature的作用大小，进行feature selection，以及我们模型下的bad case和产生的原因』等等。

• Kaggle上的大神们，也分享过一些experience：

  • 『对数据的认识太重要了！』
  • 『数据中的特殊点/离群点的分析和处理太重要了！』
  • 『特征工程(feature engineering)太重要了！在很多Kaggle的场景下，甚至比model本身还要重要』
  • 『要做模型融合(model ensemble)啊啊啊！』

# 用于Notebook一个cell里面的多行输出
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'

import pandas as pd
import numpy as np
from pandas import Series,DataFrame

1 数据初探

【要点】首先先要学会观察数据，在Data下我们train.csv和test.csv两个文件，分别存着官方给的训练和测试数据。pandas是常用的python数据处理包，把csv文件读入成dataframe格式。
【技能点】这里主要熟悉df.info()和df.describe()两个函数来观察数据。

data_train = pd.read_csv('train.csv') 
data_train

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	male	22.0	1	0	A/5 21171	7.2500	NaN	S
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th...	female	38.0	1	0	PC 17599	71.2833	C85	C
2	3	1	3	Heikkinen, Miss. Laina	female	26.0	0	0	STON/O2. 3101282	7.9250	NaN	S
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	female	35.0	1	0	113803	53.1000	C123	S
4	5	0	3	Allen, Mr. William Henry	male	35.0	0	0	373450	8.0500	NaN	S
...	...	...	...	...	...	...	...	...	...	...	...	...
886	887	0	2	Montvila, Rev. Juozas	male	27.0	0	0	211536	13.0000	NaN	S
887	888	1	1	Graham, Miss. Margaret Edith	female	19.0	0	0	112053	30.0000	B42	S
888	889	0	3	Johnston, Miss. Catherine Helen "Carrie"	female	NaN	1	2	W./C. 6607	23.4500	NaN	S
889	890	1	1	Behr, Mr. Karl Howell	male	26.0	0	0	111369	30.0000	C148	C
890	891	0	3	Dooley, Mr. Patrick	male	32.0	0	0	370376	7.7500	NaN	Q

891 rows × 12 columns

data_train.info()

RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   PassengerId  891 non-null    int64  
 1   Survived     891 non-null    int64  
 2   Pclass       891 non-null    int64  
 3   Name         891 non-null    object 
 4   Sex          891 non-null    object 
 5   Age          714 non-null    float64
 6   SibSp        891 non-null    int64  
 7   Parch        891 non-null    int64  
 8   Ticket       891 non-null    object 
 9   Fare         891 non-null    float64
 10  Cabin        204 non-null    object 
 11  Embarked     889 non-null    object 
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB

【分析】可以看出训练集有891名乘客，12个字段，第一个PassengerId由于有index，可有可无，有11个有用字段，第一个有用字段Survived，根据题意，应该作为label，其它剩余字段作为特征。观察发现Age、Cabin、Embarked三个字段有所缺失，其中Cabin缺失极其严重。而从字段类型里面可以看出，Age、Fare字段为float64（浮点小数），连续数值型精确数据。PassengerId、Survived、Pclass、SibSp、Parch字段为int64（整型），数值型，这里需要根据经验思考下它们的具体意义，整数大小是否有数字上的比较意义，还是只代表一种类型？不难看出SibSp、Parch字段为前者，而剩余的为后者。后面剩下的字段类型Name、object，Sex、Ticket、Cabin、Embarked 是文本型特征，而后面4个是类别型文本特征。

data_train.describe()

	PassengerId	Survived	Pclass	Age	SibSp	Parch	Fare
count	891.000000	891.000000	891.000000	714.000000	891.000000	891.000000	891.000000
mean	446.000000	0.383838	2.308642	29.699118	0.523008	0.381594	32.204208
std	257.353842	0.486592	0.836071	14.526497	1.102743	0.806057	49.693429
min	1.000000	0.000000	1.000000	0.420000	0.000000	0.000000	0.000000
25%	223.500000	0.000000	2.000000	20.125000	0.000000	0.000000	7.910400
50%	446.000000	0.000000	3.000000	28.000000	0.000000	0.000000	14.454200
75%	668.500000	1.000000	3.000000	38.000000	1.000000	0.000000	31.000000
max	891.000000	1.000000	3.000000	80.000000	8.000000	6.000000	512.329200

【结论】这里可以看出，统计会把非数值型的特征忽略。mean字段告诉我们，大概0.383838的人最后获救了，2/3等舱的人数比1等舱要多，平均乘客年龄大概是29.7岁(计算这个时候会略掉无记录的)等等。

2 探索性数据分析(EDA)

【思考】怎么判断哪些属性特别重要？怎么去用它们？

【经验】

• 『对数据的认识太重要了！』
  仅仅最上面对数据的了解，依旧无法给我们提供想法和思路。我们再深入一点来看看我们的数据，看看每个/多个属性和最后的Survived之间有着什么样的关系呢。

【技能点】Pandas常用的一些统计函数，用matplotlib进行数据可视化

2.1 乘客各属性分布

import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签

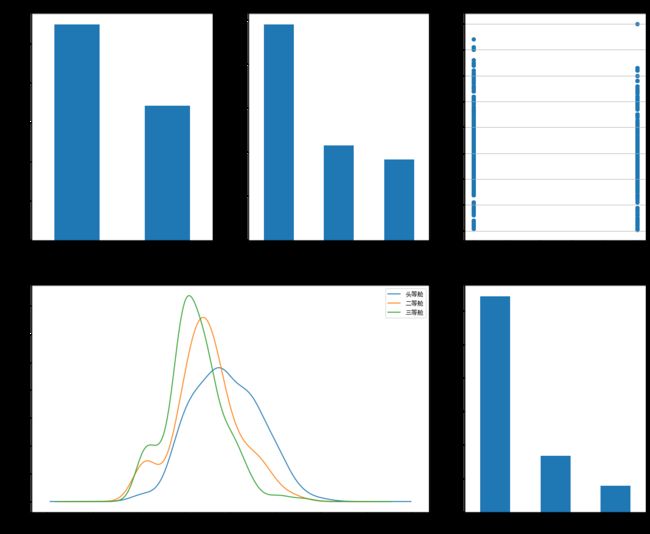
fig = plt.figure(figsize = (18,15))
fig.set()

plt.subplot2grid((2,3),(0,0))   # 在一张大图里分列几个小图
data_train['Survived'].value_counts().plot.bar()
plt.title(u'获救情况(1为获救)') # 标题
plt.ylabel(u'人数')

plt.subplot2grid((2,3),(0,1))  
data_train['Pclass'].value_counts().plot.bar()
plt.title(u'乘客等级分布')
plt.ylabel(u'人数')

plt.subplot2grid((2,3),(0,2))
plt.scatter(data_train['Survived'],data_train['Age'])
plt.title(u'按年龄看获救分布(1为获救)')
plt.ylabel(u'年龄')
plt.grid(b = True,which = 'major',axis = 'y')

plt.subplot2grid((2,3),(1,0),colspan=2) # 跨两列
data_train['Age'][data_train['Pclass'] == 1].plot.kde()
data_train['Age'][data_train['Pclass'] == 2].plot.kde()
data_train['Age'][data_train['Pclass'] == 3].plot.kde()
plt.xlabel(u'年龄')
plt.ylabel(u'密度')
plt.title(u'各等级的乘客年龄分布')
plt.legend((u'头等舱',u'二等舱',u'三等舱'),loc='best')

plt.subplot2grid((2,3),(1,2))
data_train['Embarked'].value_counts().plot.bar()
plt.title(u'人数')

【思考】从图中能得到什么信息？从中能做出什么推测吗？

【回答】
图还是比数字好看多了。所以我们在图上可以看出来，被救的人300多点，不到半数；3等舱乘客灰常多；遇难和获救的人年龄似乎跨度都很广；3个不同的舱年龄总体趋势似乎也一致，2/3等舱乘客20岁多点的人最多，1等舱40岁左右的最多(→_→似乎符合财富和年龄的分配哈，咳咳，别理我，我瞎扯的)；登船港口人数按照S、C、Q递减，而且S远多于另外俩港口。

这个时候我们可能会有一些想法了：

• 不同舱位/乘客等级可能和财富/地位有关系，最后获救概率可能会不一样
• 年龄对获救概率也一定是有影响的，毕竟前面说了，副船长还说『小孩和女士先走』呢
• 和登船港口是不是有关系呢？也许登船港口不同，人的出身地位不同？

口说无凭，空想无益。老老实实再来统计统计，看看这些属性值的统计分布吧。

2.2 属性与获救结果的关联统计

# 看看各乘客等级的获救情况
fig = plt.figure()
fig.set()

Survived_0 = data_train['Pclass'][data_train['Survived'] == 0].value_counts()
Survived_1 = data_train['Pclass'][data_train['Survived'] == 1].value_counts()
df = pd.DataFrame({
     u'未获救':Survived_0, u'获救':Survived_1})  #字典转DataFrame
df.plot.bar(stacked=True)
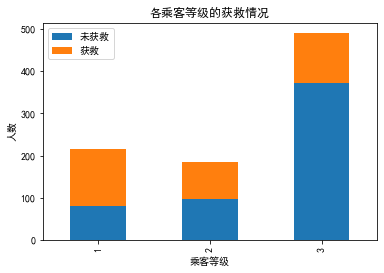
plt.title(u'各乘客等级的获救情况')
plt.xlabel(u'乘客等级')
plt.ylabel(u'人数')

【思考】舱位等级对获救情况是否有影响？

【回答】啧啧，果然，钱和地位对舱位有影响，进而对获救的可能性也有影响啊←_←
咳咳，跑题了，我想说的是，明显等级为1的乘客，获救的概率高很多。恩，这个一定是影响最后获救结果的一个特征。

# 看看各性别的获救情况
fig = plt.figure()
fig.set()

Survived_m = data_train['Survived'][data_train['Sex'] == 'male'].value_counts()
Survived_f = data_train['Survived'][data_train['Sex'] == 'female'].value_counts()
df = pd.DataFrame({
     u'男性':Survived_m, u'女性':Survived_f})  #字典转DataFrame
# data_train.groupby(['Survived','Sex'])['Survived'].count().unstack().plot(kind='bar',stacked='True')
df.plot.bar(stacked=True)
plt.title(u'各性别的获救情况（1为获救）')
plt.xlabel(u'获救情况')
plt.ylabel(u'人数')

【思考】性别对获救情况是否有影响？

【回答】歪果盆友果然很尊重lady，lady first践行得不错。性别无疑也要作为重要特征加入最后的模型之中。

 #然后我们再来看看各种舱级别情况下各性别的获救情况
fig=plt.figure(figsize=(18,12))
fig.set(alpha=0.65) # 设置图像透明度，无所谓
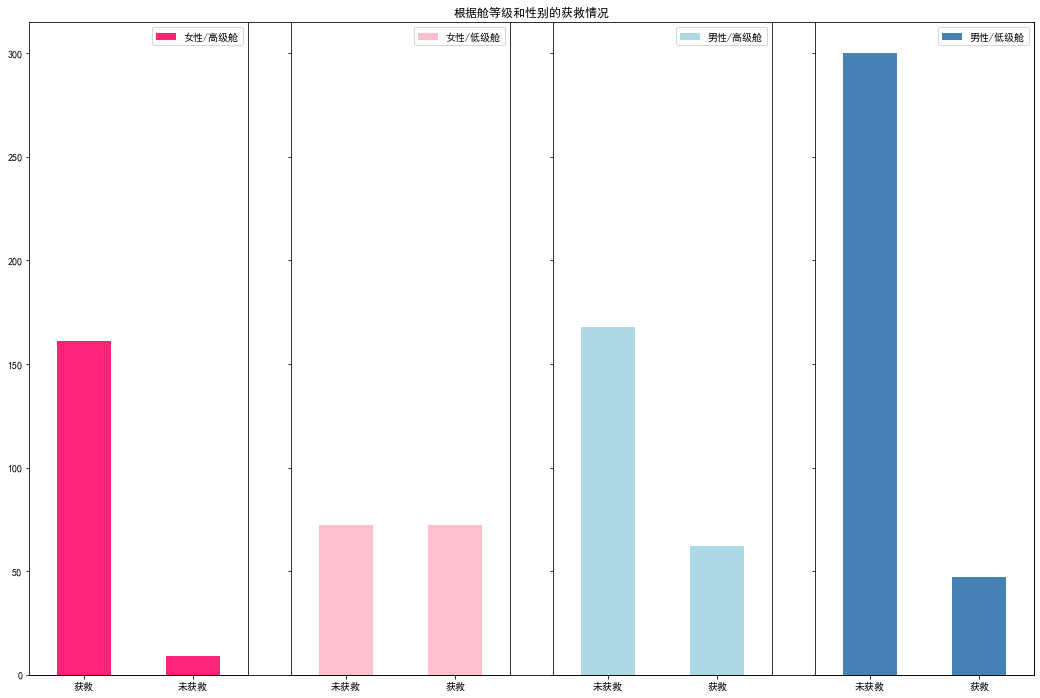
plt.title(u"根据舱等级和性别的获救情况")
plt.xticks([])  #去掉x轴
plt.yticks([])  #去掉y轴

ax1=fig.add_subplot(141)
data_train['Survived'][data_train.Sex == 'female'][data_train.Pclass != 3].value_counts().plot(kind='bar',label="female highclass", color='#FA2479')
ax1.set_xticklabels([u"获救", u"未获救"], rotation=0)
ax1.legend([u"女性/高级舱"], loc='best')

ax2=fig.add_subplot(142, sharey=ax1)
data_train.Survived[data_train.Sex == 'female'][data_train.Pclass == 3].value_counts().plot(kind='bar', label='female, low class', color='pink')
ax2.set_xticklabels([u"未获救", u"获救"], rotation=0)
plt.legend([u"女性/低级舱"], loc='best')

ax3=fig.add_subplot(143, sharey=ax1)
data_train.Survived[data_train.Sex == 'male'][data_train.Pclass != 3].value_counts().plot(kind='bar', label='male, high class',color='lightblue')
ax3.set_xticklabels([u"未获救", u"获救"], rotation=0)
plt.legend([u"男性/高级舱"], loc='best')

ax4=fig.add_subplot(144, sharey=ax1)
data_train.Survived[data_train.Sex == 'male'][data_train.Pclass == 3].value_counts().plot(kind='bar', label='male low class', color='steelblue')
ax4.set_xticklabels([u"未获救", u"获救"], rotation=0)
plt.legend([u"男性/低级舱"], loc='best')

# 我们看看各登船港口的获救情况
fig = plt.figure()
fig.set() 

Survived_0 = data_train.Embarked[data_train.Survived == 0].value_counts()
Survived_1 = data_train.Embarked[data_train.Survived == 1].value_counts()
df=pd.DataFrame({
     u'未获救':Survived_0, u'获救':Survived_1})
df.plot(kind='bar', stacked=True)
# data_train.groupby(['Embarked','Survived'])['Embarked'].count().unstack().plot(kind='bar',stacked='True')
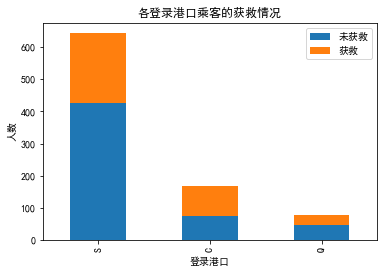
plt.title(u"各登录港口乘客的获救情况")
plt.xlabel(u"登录港口") 
plt.ylabel(u"人数") 

# 下面我们来看看 堂兄弟/妹，孩子/父母有几人，对是否获救的影响。
g = data_train.groupby(['SibSp','Survived'])
df = pd.DataFrame(g.count()['PassengerId'])
df

g = data_train.groupby(['Parch','Survived'])
df = pd.DataFrame(g.count()['PassengerId'])
df

		PassengerId
SibSp	Survived
0	0	398
	1	210
1	0	97
	1	112
2	0	15
	1	13
3	0	12
	1	4
4	0	15
	1	3
5	0	5
8	0	7

		PassengerId
Parch	Survived
0	0	445
	1	233
1	0	53
	1	65
2	0	40
	1	40
3	0	2
	1	3
4	0	4
5	0	4
	1	1
6	0	1

#ticket是船票编号，应该是unique的，和最后的结果没有太大的关系，先不纳入考虑的特征范畴把
#cabin只有204个乘客有值，我们先看看它的一个分布
data_train.Cabin.value_counts()

G6             4
B96 B98        4
C23 C25 C27    4
E101           3
F33            3
              ..
B102           1
B94            1
E34            1
D49            1
E40            1
Name: Cabin, Length: 147, dtype: int64

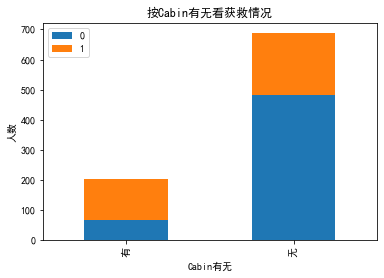
【思考】 Cabin这个属性缺失值很多，如果直接按照类目特征处理的话，太散了，估计每个因子化后的特征都拿不到什么权重。加上有那么多缺失值，要不我们先把Cabin缺失与否作为条件(虽然这部分信息缺失可能并非未登记，maybe只是丢失了而已，所以这样做未必妥当)，先在有无Cabin信息这个粗粒度上看看Survived的情况好了。

fig = plt.figure()
fig.set()  

Survived_cabin = data_train.Survived[pd.notnull(data_train.Cabin)].value_counts()
Survived_nocabin = data_train.Survived[pd.isnull(data_train.Cabin)].value_counts()
# pd.DataFrame({u'有':Survived_cabin, u'无':Survived_nocabin})
# pd.DataFrame({u'有':Survived_cabin, u'无':Survived_nocabin}).transpose()
df=pd.DataFrame({
     u'有':Survived_cabin, u'无':Survived_nocabin}).transpose() # 调换数组的行列值的索引值
df.plot(kind='bar', stacked=True)
plt.title(u"按Cabin有无看获救情况")
plt.xlabel(u"Cabin有无") 
plt.ylabel(u"人数")

【结论】有Cabin记录的似乎获救概率稍高一些

3 数据预处理

【技能点】Pandas的条件索引查找，数据凭借重构，数据类型转换，sk-learn的随机森林的使用。

【思考】

大体数据的情况看了一遍，对感兴趣的属性也有个大概的了解了。
下一步干啥？咱们该处理处理这些数据，为机器学习建模做点准备了。

对了，我这里说的数据预处理，其实就包括了很多Kaggler津津乐道的feature engineering过程，灰常灰常有必要！

『特征工程(feature engineering)太重要了！』

大体过了一遍数据，对感兴趣的属性也有大概的了解。下面该对数据进行预处理，为机器学习建模做准备。

先从最突出的数据属性开始吧，对，Cabin和Age，有丢失数据实在是对下一步工作影响太大。

先说Cabin，暂时我们就按照刚才说的，按Cabin有无数据，将这个属性处理成Yes和No两种类型吧。

再说Age：

通常遇到缺值的情况，我们会有几种常见的处理方式

1. 如果缺值的样本占总数比例极高，我们可能就直接舍弃了，作为特征加入的话，可能反倒带入noise，影响最后的结果了。（比如这里的的Cabin）
2. 如果缺值的样本适中，而该属性非连续值特征属性(比如说类目属性)，那就把NaN作为一个新类别，加到类别特征中。
3. 如果缺值的样本适中，而该属性为连续值特征属性，有时候我们会考虑给定一个step(比如这里的age，我们可以考虑每隔2/3岁为一个步长)，然后把它离散化，之后把NaN作为一个type加到属性类目中。（比如这里的Age字段）
4. 有些情况下，缺失的值个数并不是特别多，那我们也可以试着根据已有的值，拟合一下数据，补充上。（比如这里的Embarked字段或者Age字段）

我们这里用scikit-learn中的RandomForest来拟合一下缺失的年龄数据(注：RandomForest是一个用在原始数据中做不同采样，建立多颗DecisionTree，再进行average等等来降低过拟合现象，提高结果的机器学习算法）

from sklearn.ensemble import RandomForestRegressor
 
### 使用 RandomForestClassifier 填补缺失的年龄属性
def set_missing_ages(df):
    
    # 把已有的有用的数值型特征取出来丢进Random Forest Regressor中
    age_df = df[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]

    # 乘客分成已知年龄和未知年龄两部分
    known_age = age_df[age_df.Age.notnull()].values # 这会形成一个二维数组，想象成一个矩阵
    unknown_age = age_df[age_df.Age.isnull()].values

    # y即目标年龄
    y = known_age[:, 0]

    # X即特征属性值
    X = known_age[:, 1:]

    # fit到RandomForestRegressor之中
    rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)  # -1表示所有处理器并行处理
    rfr.fit(X, y)
    
    # 用得到的模型进行未知年龄结果预测
    predictedAges = rfr.predict(unknown_age[:, 1:])
    
    # 用得到的预测结果填补原缺失数据
    df.loc[ (df.Age.isnull()), 'Age' ] = predictedAges 
    
    return df, rfr

def set_Cabin_type(df):
    df.loc[ (df.Cabin.notnull()), 'Cabin' ] = "Yes"
    df.loc[ (df.Cabin.isnull()), 'Cabin' ] = "No"
    return df

data_train, rfr = set_missing_ages(data_train)
data_train = set_Cabin_type(data_train)

data_train 

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	male	22.00000	1	0	A/5 21171	7.2500	No	S
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th...	female	38.00000	1	0	PC 17599	71.2833	Yes	C
2	3	1	3	Heikkinen, Miss. Laina	female	26.00000	0	0	STON/O2. 3101282	7.9250	No	S
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	female	35.00000	1	0	113803	53.1000	Yes	S
4	5	0	3	Allen, Mr. William Henry	male	35.00000	0	0	373450	8.0500	No	S
...	...	...	...	...	...	...	...	...	...	...	...	...
886	887	0	2	Montvila, Rev. Juozas	male	27.00000	0	0	211536	13.0000	No	S
887	888	1	1	Graham, Miss. Margaret Edith	female	19.00000	0	0	112053	30.0000	Yes	S
888	889	0	3	Johnston, Miss. Catherine Helen "Carrie"	female	16.19395	1	2	W./C. 6607	23.4500	No	S
889	890	1	1	Behr, Mr. Karl Howell	male	26.00000	0	0	111369	30.0000	Yes	C
890	891	0	3	Dooley, Mr. Patrick	male	32.00000	0	0	370376	7.7500	No	Q

891 rows × 12 columns

【参考】https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html

【拓展】
Pandas数据查找常用方法

1. 选取某一整行（多个整行）或某一整列（多个整列）数据时，可以用df[]、df.loc[]、df.iloc[]，此时df[]的方法书写要简单一些。

2. 进行区域选取时，如果只能用标签索引，则使用df.loc[]或df.ix[]，如果只能用整数索引，则用df.iloc[]或df.ix[]。不过我看到有资料说，不建议使用df.ix[],因为df.loc[]和df.iloc[]更精确（有吗？我没理解精确在哪，望告知）。

3. 如果选取单元格，则df.at[]、df.iat[]、df.loc[]、df.iloc[]都可以，不过要注意参数。

4. 选取数据时，返回值存在以下情况：

   • 如果返回值包括单行多列或多行单列时，返回值为Series对象；
   • 如果返回值包括多行多列时，返回值为DataFrame对象；
   • 如果返回值仅为一个单元格（单行单列）时，返回值为基本数据类型，例如str，int等。

5. df[]的方式只能选取行和列数据，不能精确到单元格，所以df[]的返回值一定DataFrame或Series对象。

6. 当使用DataFrame的默认索引（整数索引）时，整数索引即为标签索引。例如，使用上面的data实例化一个DataFrame对象：

【参考】python数据分析之pandas数据选取：df[] df.loc[] df.iloc[] df.ix[] df.at[] df.iat[]

逻辑回归建模时，需要输入的特征都是数值型特征，我们通常会先对类目型的特征因子化。

我们使用pandas的"get_dummies"来完成这个工作，并拼接在原来的"data_train"之上，如下所示。

# One-hot encode
for feat in ['Cabin', 'Embarked', 'Sex', 'Pclass']:
    x = pd.get_dummies(data_train[feat], prefix = feat)
    data_train = pd.concat([data_train, x], axis = 1)
      
data_train.drop(['Cabin', 'Embarked', 'Sex', 'Pclass', 'Name', 'Ticket'], axis = 1, inplace = True)
data_train

	PassengerId	Survived	Age	SibSp	Parch	Fare	Cabin_No	Cabin_Yes	Embarked_C	Embarked_Q	Embarked_S	Sex_female	Sex_male	Pclass_1	Pclass_2	Pclass_3
0	1	0	22.00000	1	0	7.2500	1	0	0	0	1	0	1	0	0	1
1	2	1	38.00000	1	0	71.2833	0	1	1	0	0	1	0	1	0	0
2	3	1	26.00000	0	0	7.9250	1	0	0	0	1	1	0	0	0	1
3	4	1	35.00000	1	0	53.1000	0	1	0	0	1	1	0	1	0	0
4	5	0	35.00000	0	0	8.0500	1	0	0	0	1	0	1	0	0	1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
886	887	0	27.00000	0	0	13.0000	1	0	0	0	1	0	1	0	1	0
887	888	1	19.00000	0	0	30.0000	0	1	0	0	1	1	0	1	0	0
888	889	0	16.19395	1	2	23.4500	1	0	0	0	1	1	0	0	0	1
889	890	1	26.00000	0	0	30.0000	0	1	1	0	0	0	1	1	0	0
890	891	0	32.00000	0	0	7.7500	1	0	0	1	0	0	1	0	0	1

891 rows × 16 columns

# 另一种方法，不会覆盖data_train

# dummies_Cabin = pd.get_dummies(data_train['Cabin'], prefix= 'Cabin')

# dummies_Embarked = pd.get_dummies(data_train['Embarked'], prefix= 'Embarked')

# dummies_Sex = pd.get_dummies(data_train['Sex'], prefix= 'Sex')

# dummies_Pclass = pd.get_dummies(data_train['Pclass'], prefix= 'Pclass')

# df = pd.concat([data_train, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
# df.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)
# df

这样，看起来，是不是我们需要的属性值都有了，且它们都是数值型属性呢。

有我们还得做一些处理，仔细看看Age和Fare两个属性，乘客的数值幅度变化，也忒大了吧！！如果大家了解逻辑回归与梯度下降的话，会知道，各属性值之间scale差距太大，将对收敛速度造成几万点伤害值！甚至不收敛！ (╬▔皿▔)…所以我们先用scikit-learn里面的preprocessing模块对这俩货做一个scaling，所谓scaling，其实就是将一些变化幅度较大的特征化到[-1,1]之内。

df = data_train
import sklearn.preprocessing as preprocessing
scaler = preprocessing.StandardScaler()
age_scale_param = scaler.fit(df[['Age']]) # 注意，一个[]是series，两个是array
df['Age_scaled'] = scaler.fit_transform(df[['Age']], age_scale_param) # fit_transform(X, y=None, **fit_params)
fare_scale_param = scaler.fit(df[['Fare']])
df['Fare_scaled'] = scaler.fit_transform(df[['Fare']], fare_scale_param)
df

	PassengerId	Survived	Age	SibSp	Parch	Fare	Cabin_No	Cabin_Yes	Embarked_C	Embarked_Q	Embarked_S	Sex_female	Sex_male	Pclass_1	Pclass_2	Pclass_3	Age_scaled	Fare_scaled
0	1	0	22.00000	1	0	7.2500	1	0	0	0	1	0	1	0	0	1	-0.561380	-0.502445
1	2	1	38.00000	1	0	71.2833	0	1	1	0	0	1	0	1	0	0	0.613171	0.786845
2	3	1	26.00000	0	0	7.9250	1	0	0	0	1	1	0	0	0	1	-0.267742	-0.488854
3	4	1	35.00000	1	0	53.1000	0	1	0	0	1	1	0	1	0	0	0.392942	0.420730
4	5	0	35.00000	0	0	8.0500	1	0	0	0	1	0	1	0	0	1	0.392942	-0.486337
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
886	887	0	27.00000	0	0	13.0000	1	0	0	0	1	0	1	0	1	0	-0.194333	-0.386671
887	888	1	19.00000	0	0	30.0000	0	1	0	0	1	1	0	1	0	0	-0.781608	-0.044381
888	889	0	16.19395	1	2	23.4500	1	0	0	0	1	1	0	0	0	1	-0.987599	-0.176263
889	890	1	26.00000	0	0	30.0000	0	1	1	0	0	0	1	1	0	0	-0.267742	-0.044381
890	891	0	32.00000	0	0	7.7500	1	0	0	1	0	0	1	0	0	1	0.172714	-0.492378

891 rows × 18 columns

【参考】https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html

万事俱备，只欠建模。马上就要看到成效了，哈哈。我们把需要的属性值抽出来，转成scikit-learn里面LogisticRegression可以处理的格式。

4 逻辑斯蒂回归建模

【技能点】sklearn的线性模型Logistic Regression使用，正则表达式，Pandas的过滤提取

from sklearn.linear_model import LogisticRegression

# 用正则表达式提取出我们要的属性值
train_df = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*') # DataFrame.filter(items=None, like=None, regex=None, axis=None)
train_np = train_df.values

# y即Survival结果
y = train_np[:, 0]

# X即特征属性值
X = train_np[:, 1:]

# fit到RandomForestRegressor之中
clf = LogisticRegression(C=1.0, penalty='l1', solver='liblinear', tol=1e-6)  # 用的是L1正则化
clf.fit(X, y)

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='warn', n_jobs=None, penalty='l1',
                   random_state=None, solver='liblinear', tol=1e-06, verbose=0,
                   warm_start=False)

【参考】你是如何学会正则表达式的？
    pandas.DataFrame.filterpandas.DataFrame.filter
    https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
    Sklearn-LogisticRegression逻辑回归

"test_data"也要做和"train_data"一样的预处理

data_test = pd.read_csv("test.csv")
data_test.loc[ (data_test.Fare.isnull()), 'Fare' ] = 0
# 接着我们对test_data做和train_data中一致的特征变换
# 首先用同样的RandomForestRegressor模型填上丢失的年龄
tmp_df = data_test[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
null_age = tmp_df[data_test.Age.isnull()].values
# 根据特征属性X预测年龄并补上
X = null_age[:, 1:]
predictedAges = rfr.predict(X)
data_test.loc[ (data_test.Age.isnull()), 'Age' ] = predictedAges

data_test = set_Cabin_type(data_test)
dummies_Cabin = pd.get_dummies(data_test['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_test['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_test['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_test['Pclass'], prefix= 'Pclass')


df_test = pd.concat([data_test, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
df_test.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)
df_test['Age_scaled'] = scaler.fit_transform(df_test[['Age']], age_scale_param)
df_test['Fare_scaled'] = scaler.fit_transform(df_test[['Fare']], fare_scale_param)
df_test

	PassengerId	Age	SibSp	Parch	Fare	Cabin_No	Cabin_Yes	Embarked_C	Embarked_Q	Embarked_S	Sex_female	Sex_male	Pclass_1	Pclass_2	Pclass_3	Age_scaled	Fare_scaled
0	892	34.500000	0	0	7.8292	1	0	0	1	0	0	1	0	0	1	0.307521	-0.496637
1	893	47.000000	1	0	7.0000	1	0	0	0	1	1	0	0	0	1	1.256241	-0.511497
2	894	62.000000	0	0	9.6875	1	0	0	1	0	0	1	0	1	0	2.394706	-0.463335
3	895	27.000000	0	0	8.6625	1	0	0	0	1	0	1	0	0	1	-0.261711	-0.481704
4	896	22.000000	1	1	12.2875	1	0	0	0	1	1	0	0	0	1	-0.641199	-0.416740
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
413	1305	30.705727	0	0	8.0500	1	0	0	0	1	0	1	0	0	1	0.019545	-0.492680
414	1306	39.000000	0	0	108.9000	0	1	1	0	0	1	0	1	0	0	0.649061	1.314641
415	1307	38.500000	0	0	7.2500	1	0	0	0	1	0	1	0	0	1	0.611112	-0.507017
416	1308	30.705727	0	0	8.0500	1	0	0	0	1	0	1	0	0	1	0.019545	-0.492680
417	1309	25.783377	1	1	22.3583	1	0	1	0	0	0	1	0	0	1	-0.354050	-0.236263

418 rows × 17 columns

【建议】这里其实可以把训练集和测试集拼接在一起做预处理，然后再拆分回去。

下面就做预测取结果吧！

test = df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
predictions = clf.predict(test)
result = pd.DataFrame({
     'PassengerId':data_test['PassengerId'].values, 'Survived':predictions.astype(np.int64)})
result.to_csv("logistic_regression_predictions.csv", index=False)

result

	PassengerId	Survived
0	892	0
1	893	0
2	894	0
3	895	0
4	896	1
...	...	...
413	1305	0
414	1306	1
415	1307	0
416	1308	0
417	1309	0

418 rows × 2 columns

查看表格发现格式没问题，很好，baseline模型完成！去kaggle上提交结果。

在Kaggle的Make a submission页面，提交上结果。现在要学会科学上网才能上传，结果如下：

有点惨啊！大哥！

5 逻辑斯蒂回归系统优化

5.1 模型关联系数分析

亲，你以为结果提交上了，就完事了？
我不会告诉你，这只是万里长征第一步啊(泪牛满面)！！！这才刚撸完baseline model啊！！！还得优化啊！！！

看过Andrew Ng老师的machine Learning课程的同学们，知道，我们应该分析分析模型现在的状态了，是过/欠拟合？，以确定我们需要更多的特征还是更多数据，或者其他操作。我们有一条很著名的learning curves对吧。

不过在现在的场景下，先不着急做这个事情，我们这个baseline系统还有些粗糙，先再挖掘挖掘。

首先，Name和Ticket两个属性被我们完整舍弃了(好吧，其实是因为这俩属性，几乎每一条记录都是一个完全不同的值，我们并没有找到很直接的处理方式)。

然后，我们想想，年龄的拟合本身也未必是一件非常靠谱的事情，我们依据其余属性，其实并不能很好地拟合预测出未知的年龄。再一个，以我们的日常经验，小盆友和老人可能得到的照顾会多一些，这样看的话，年龄作为一个连续值，给一个固定的系数，应该和年龄是一个正相关或者负相关，似乎体现不出两头受照顾的实际情况，所以，说不定我们把年龄离散化，按区段分作类别属性会更合适一些。

上面只是我瞎想的，who knows是不是这么回事呢，老老实实先把得到的model系数和feature关联起来看看。

pd.DataFrame({
     "columns":list(train_df.columns)[1:], "coef":list(clf.coef_.T)})

	columns	coef
0	SibSp	[-0.34423573629293847]
1	Parch	[-0.10491571108768365]
2	Cabin_No	[0.0]
3	Cabin_Yes	[0.9021086924754858]
4	Embarked_C	[0.0]
5	Embarked_Q	[0.0]
6	Embarked_S	[-0.41726209813327236]
7	Sex_female	[1.9565685339978756]
8	Sex_male	[-0.6774231575312185]
9	Pclass_1	[0.34116093849618767]
10	Pclass_2	[0.0]
11	Pclass_3	[-1.1941287019944846]
12	Age_scaled	[-0.5237666077227154]
13	Fare_scaled	[0.08443478623821545]

【结论】
我们先看看那些权重绝对值非常大的feature，在我们的模型上：

• Sex属性，如果是female会极大提高最后获救的概率，而male会很大程度拉低这个概率。
• Pclass属性，1等舱乘客最后获救的概率会上升，而乘客等级为3会极大地拉低这个概率。
• 有Cabin值会很大程度拉升最后获救概率(这里似乎能看到了一点端倪，事实上从最上面的有无Cabin记录的Survived分布图上看出，即使有Cabin记录的乘客也有一部分遇难了，估计这个属性上我们挖掘还不够)
• Age是一个负相关，意味着在我们的模型里，年龄越小，越有获救的优先权(还得回原数据看看这个是否合理）
• 有一个登船港口S会很大程度拉低获救的概率，另外俩港口压根就没啥作用(这个实际上非常奇怪，因为我们从之前的统计图上并没有看到S港口的获救率非常低，所以也许可以考虑把登船港口这个feature去掉试试)。
• 船票Fare有小幅度的正相关(并不意味着这个feature作用不大，有可能是我们细化的程度还不够，举个例子，说不定我们得对它离散化，再分至各个乘客等级上？)

噢啦，观察完了，我们现在有一些想法了，但是怎么样才知道，哪些优化的方法是promising的呢？

因为test.csv里面并没有Survived这个字段(好吧，这是废话，这明明就是我们要预测的结果)，我们无法在这份数据上评定我们算法在该场景下的效果…

而『每做一次调整就make a submission，然后根据结果来判定这次调整的好坏』其实是行不通的…

5.2 交叉验证

重点又来了：

『要做交叉验证(cross validation)!』

恩，重要的事情说三遍。我们通常情况下，这么做cross validation：把train.csv分成两部分，一部分用于训练我们需要的模型，另外一部分数据上看我们预测算法的效果。

我们用scikit-learn的cross_validation来帮我们完成小数据集上的这个工作。

先简单看看cross validation情况下的打分

from sklearn import linear_model
from sklearn import model_selection

 #简单看看打分情况
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', solver='liblinear', tol=1e-6)
all_data = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
X = all_data.values[:,1:]
y = all_data.values[:,0]
model_selection.cross_val_score(clf, X, y, cv = 5) #5折交叉验证分数

array([0.81564246, 0.81564246, 0.78651685, 0.78651685, 0.81355932])

似乎比Kaggle上的结果略高哈，毕竟用的是不是同一份数据集评估的。

等等，既然我们要做交叉验证，那我们干脆先把交叉验证里面的bad case拿出来看看，看看人眼审核，是否能发现什么蛛丝马迹，是我们忽略了哪些信息，使得这些乘客被判定错了。再把bad case上得到的想法和前头系数分析的合在一起，然后逐个试试。

下面我们做数据分割，并且在原始数据集上瞄一眼bad case：

# 分割数据，按照 训练数据:cv数据 = 7:3的比例
# split_train, split_cv = cross_validation.train_test_split(df, test_size=0.3, random_state=0)
from sklearn.model_selection import train_test_split
split_train, split_cv = train_test_split(df, test_size=0.3, random_state=0)
train_df = split_train.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
# 生成模型
clf = linear_model.LogisticRegression(C=1.0, penalty='l1',solver='liblinear', tol=1e-6)
clf.fit(train_df.values[:,1:], train_df.values[:,0])

# 对cross validation数据进行预测

cv_df = split_cv.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
predictions = clf.predict(cv_df.values[:,1:])

origin_data_train = pd.read_csv("train.csv")
bad_cases = origin_data_train.loc[origin_data_train['PassengerId'].isin(split_cv[predictions != cv_df.values[:,0]]['PassengerId'].values)]
bad_cases

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='warn', n_jobs=None, penalty='l1',
                   random_state=None, solver='liblinear', tol=1e-06, verbose=0,
                   warm_start=False)

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
14	15	0	3	Vestrom, Miss. Hulda Amanda Adolfina	female	14.00	0	0	350406	7.8542	NaN	S
49	50	0	3	Arnold-Franchi, Mrs. Josef (Josefine Franchi)	female	18.00	1	0	349237	17.8000	NaN	S
55	56	1	1	Woolner, Mr. Hugh	male	NaN	0	0	19947	35.5000	C52	S
65	66	1	3	Moubarek, Master. Gerios	male	NaN	1	1	2661	15.2458	NaN	C
68	69	1	3	Andersson, Miss. Erna Alexandra	female	17.00	4	2	3101281	7.9250	NaN	S
85	86	1	3	Backstrom, Mrs. Karl Alfred (Maria Mathilda Gu...	female	33.00	3	0	3101278	15.8500	NaN	S
113	114	0	3	Jussila, Miss. Katriina	female	20.00	1	0	4136	9.8250	NaN	S
140	141	0	3	Boulos, Mrs. Joseph (Sultana)	female	NaN	0	2	2678	15.2458	NaN	C
204	205	1	3	Cohen, Mr. Gurshon "Gus"	male	18.00	0	0	A/5 3540	8.0500	NaN	S
240	241	0	3	Zabour, Miss. Thamine	female	NaN	1	0	2665	14.4542	NaN	C
251	252	0	3	Strom, Mrs. Wilhelm (Elna Matilda Persson)	female	29.00	1	1	347054	10.4625	G6	S
261	262	1	3	Asplund, Master. Edvin Rojj Felix	male	3.00	4	2	347077	31.3875	NaN	S
264	265	0	3	Henry, Miss. Delia	female	NaN	0	0	382649	7.7500	NaN	Q
267	268	1	3	Persson, Mr. Ernst Ulrik	male	25.00	1	0	347083	7.7750	NaN	S
271	272	1	3	Tornquist, Mr. William Henry	male	25.00	0	0	LINE	0.0000	NaN	S
279	280	1	3	Abbott, Mrs. Stanton (Rosa Hunt)	female	35.00	1	1	C.A. 2673	20.2500	NaN	S
283	284	1	3	Dorking, Mr. Edward Arthur	male	19.00	0	0	A/5. 10482	8.0500	NaN	S
293	294	0	3	Haas, Miss. Aloisia	female	24.00	0	0	349236	8.8500	NaN	S
298	299	1	1	Saalfeld, Mr. Adolphe	male	NaN	0	0	19988	30.5000	C106	S
301	302	1	3	McCoy, Mr. Bernard	male	NaN	2	0	367226	23.2500	NaN	Q
312	313	0	2	Lahtinen, Mrs. William (Anna Sylfven)	female	26.00	1	1	250651	26.0000	NaN	S
338	339	1	3	Dahl, Mr. Karl Edwart	male	45.00	0	0	7598	8.0500	NaN	S
362	363	0	3	Barbara, Mrs. (Catherine David)	female	45.00	0	1	2691	14.4542	NaN	C
390	391	1	1	Carter, Mr. William Ernest	male	36.00	1	2	113760	120.0000	B96 B98	S
402	403	0	3	Jussila, Miss. Mari Aina	female	21.00	1	0	4137	9.8250	NaN	S
447	448	1	1	Seward, Mr. Frederic Kimber	male	34.00	0	0	113794	26.5500	NaN	S
474	475	0	3	Strandberg, Miss. Ida Sofia	female	22.00	0	0	7553	9.8375	NaN	S
483	484	1	3	Turkula, Mrs. (Hedwig)	female	63.00	0	0	4134	9.5875	NaN	S
489	490	1	3	Coutts, Master. Eden Leslie "Neville"	male	9.00	1	1	C.A. 37671	15.9000	NaN	S
501	502	0	3	Canavan, Miss. Mary	female	21.00	0	0	364846	7.7500	NaN	Q
503	504	0	3	Laitinen, Miss. Kristina Sofia	female	37.00	0	0	4135	9.5875	NaN	S
505	506	0	1	Penasco y Castellana, Mr. Victor de Satode	male	18.00	1	0	PC 17758	108.9000	C65	C
564	565	0	3	Meanwell, Miss. (Marion Ogden)	female	NaN	0	0	SOTON/O.Q. 392087	8.0500	NaN	S
567	568	0	3	Palsson, Mrs. Nils (Alma Cornelia Berglund)	female	29.00	0	4	349909	21.0750	NaN	S
570	571	1	2	Harris, Mr. George	male	62.00	0	0	S.W./PP 752	10.5000	NaN	S
587	588	1	1	Frolicher-Stehli, Mr. Maxmillian	male	60.00	1	1	13567	79.2000	B41	C
642	643	0	3	Skoog, Miss. Margit Elizabeth	female	2.00	3	2	347088	27.9000	NaN	S
643	644	1	3	Foo, Mr. Choong	male	NaN	0	0	1601	56.4958	NaN	S
647	648	1	1	Simonius-Blumer, Col. Oberst Alfons	male	56.00	0	0	13213	35.5000	A26	C
654	655	0	3	Hegarty, Miss. Hanora "Nora"	female	18.00	0	0	365226	6.7500	NaN	Q
680	681	0	3	Peters, Miss. Katie	female	NaN	0	0	330935	8.1375	NaN	Q
712	713	1	1	Taylor, Mr. Elmer Zebley	male	48.00	1	0	19996	52.0000	C126	S
740	741	1	1	Hawksford, Mr. Walter James	male	NaN	0	0	16988	30.0000	D45	S
762	763	1	3	Barah, Mr. Hanna Assi	male	20.00	0	0	2663	7.2292	NaN	C
788	789	1	3	Dean, Master. Bertram Vere	male	1.00	1	2	C.A. 2315	20.5750	NaN	S
803	804	1	3	Thomas, Master. Assad Alexander	male	0.42	0	1	2625	8.5167	NaN	C
838	839	1	3	Chip, Mr. Chang	male	32.00	0	0	1601	56.4958	NaN	S
839	840	1	1	Marechal, Mr. Pierre	male	NaN	0	0	11774	29.7000	C47	C
852	853	0	3	Boulos, Miss. Nourelain	female	9.00	1	1	2678	15.2458	NaN	C
882	883	0	3	Dahlberg, Miss. Gerda Ulrika	female	22.00	0	0	7552	10.5167	NaN	S

大家可以自己跑一遍试试，拿到bad cases之后，仔细看看。也会有一些猜测和想法。其中会有一部分可能会印证在系数分析部分的猜测，那这些优化的想法优先级可以放高一些。

现在有了"train_df" 和 “vc_df” 两个数据部分，前者用于训练model，后者用于评定和选择模型。可以开始可劲折腾了。

我们随便列一些可能可以做的优化操作：

• Age属性不使用现在的拟合方式，而是根据名称中的『Mr』『Mrs』『Miss』等的平均值进行填充。
• Age不做成一个连续值属性，而是使用一个步长进行离散化，变成离散的类目feature。
• Cabin再细化一些，对于有记录的Cabin属性，我们将其分为前面的字母部分(我猜是位置和船层之类的信息) 和 后面的数字部分(应该是房间号，有意思的事情是，如果你仔细看看原始数据，你会发现，这个值大的情况下，似乎获救的可能性高一些)。
• Pclass和Sex俩太重要了，我们试着用它们去组出一个组合属性来试试，这也是另外一种程度的细化。
• 单加一个Child字段，Age<=12的，设为1，其余为0(你去看看数据，确实小盆友优先程度很高啊)
• 如果名字里面有『Mrs』，而Parch>1的，我们猜测她可能是一个母亲，应该获救的概率也会提高，因此可以多加一个Mother字段，此种情况下设为1，其余情况下设为0
• 登船港口可以考虑先去掉试试(Q和C本来就没权重，S有点诡异)
• 把堂兄弟/兄妹 和 Parch 还有自己 个数加在一起组一个Family_size字段(考虑到大家族可能对最后的结果有影响)
• Name是一个我们一直没有触碰的属性，我们可以做一些简单的处理，比如说男性中带某些字眼的(‘Capt’, ‘Don’, ‘Major’, ‘Sir’)可以统一到一个Title，女性也一样。

大家接着往下挖掘，可能还可以想到更多可以细挖的部分。我这里先列这些了，然后我们可以使用手头上的"train_df"和"cv_df"开始试验这些feature engineering的tricks是否有效了。

试验的过程比较漫长，也需要有耐心，而且我们经常会面临很尴尬的状况，就是我们灵光一闪，想到一个feature，然后坚信它一定有效，结果试验下来，效果还不如试验之前的结果。恩，需要坚持和耐心，以及不断的挖掘。

我最好的结果是在『Survived~C(Pclass)+C(Title)+C(Sex)+C(Age_bucket)+C(Cabin_num_bucket)Mother+Fare+Family_Size』下取得的，结果如下(抱歉，博主君commit的时候手抖把页面关了，于是没截着图，下面这张图是在我得到最高分之后，用这次的结果重新make commission的，截了个图，得分是0.79426，不是目前我的最高分哈，因此排名木有变…)

6 learning curves

有一个很可能发生的问题是，我们不断地做feature engineering，产生的特征越来越多，用这些特征去训练模型，会对我们的训练集拟合得越来越好，同时也可能在逐步丧失泛化能力，从而在待预测的数据上，表现不佳，也就是发生过拟合问题。

从另一个角度上说，如果模型在待预测的数据上表现不佳，除掉上面说的过拟合问题，也有可能是欠拟合问题，也就是说在训练集上，其实拟合的也不是那么好。

额，这个欠拟合和过拟合怎么解释呢。这么说吧：

• 过拟合就像是你班那个学数学比较刻板的同学，老师讲过的题目，一字不漏全记下来了，于是老师再出一样的题目，分分钟精确出结果。but数学考试，因为总是碰到新题目，所以成绩不咋地。
• 欠拟合就像是，咳咳，和博主level差不多的差生。连老师讲的练习题也记不住，于是连老师出一样题目复习的周测都做不好，考试更是可想而知了。

而在机器学习的问题上，对于过拟合和欠拟合两种情形。我们优化的方式是不同的。

对过拟合而言，通常以下策略对结果优化是有用的：

• 做一下feature selection，挑出较好的feature的subset来做training
• 提供更多的数据，从而弥补原始数据的bias问题，学习到的model也会更准确

而对于欠拟合而言，我们通常需要更多的feature，更复杂的模型来提高准确度。

著名的learning curve可以帮我们判定我们的模型现在所处的状态。我们以样本数为横坐标，训练和交叉验证集上的错误率作为纵坐标，两种状态分别如下两张图所示：过拟合(overfitting/high variace)，欠拟合(underfitting/high bias)

我们也可以把错误率替换成准确率(得分)，得到另一种形式的learning curve(sklearn 里面是这么做的)。

回到我们的问题，我们用scikit-learn里面的learning_curve来帮我们分辨我们模型的状态。举个例子，这里我们一起画一下我们最先得到的baseline model的learning curve。

import numpy as np
import matplotlib.pyplot as plt
# from sklearn.learning_curve import learning_curve 修改以fix learning_curve DeprecationWarning
from sklearn.model_selection import learning_curve

# 用sklearn的learning_curve得到training_score和cv_score，使用matplotlib画出learning curve
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=3, n_jobs=1, 
                        train_sizes=np.linspace(.05, 1., 20), verbose=0, plot=True): #注意新版默认为5，不是3
    """
    画出data在某模型上的learning curve.
    参数解释
    ----------
    estimator : 你用的分类器。
    title : 表格的标题。
    X : 输入的feature，numpy类型
    y : 输入的target vector
    ylim : tuple格式的(ymin, ymax), 设定图像中纵坐标的最低点和最高点
    cv : 做cross-validation的时候，数据分成的份数，其中一份作为cv集，其余n-1份作为training(默认为5份)
    n_jobs : 并行的的任务数(默认1)
    """
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes, verbose=verbose)
    
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    
    if plot:
        plt.figure()
        plt.title(title)
        if ylim is not None:
            plt.ylim(*ylim)
        plt.xlabel(u"训练样本数")
        plt.ylabel(u"得分")
        plt.gca().invert_yaxis()
        plt.grid()
    
        plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, 
                         alpha=0.1, color="b")
        plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, 
                         alpha=0.1, color="r")
        plt.plot(train_sizes, train_scores_mean, 'o-', color="b", label=u"训练集上得分")
        plt.plot(train_sizes, test_scores_mean, 'o-', color="r", label=u"交叉验证集上得分")
    
        plt.legend(loc="best")
        
        plt.draw()
        plt.gca().invert_yaxis() #原文这里顺序有问题
        plt.show()
    
    midpoint = ((train_scores_mean[-1] + train_scores_std[-1]) + (test_scores_mean[-1] - test_scores_std[-1])) / 2
    diff = (train_scores_mean[-1] + train_scores_std[-1]) - (test_scores_mean[-1] - test_scores_std[-1])
    return midpoint, diff

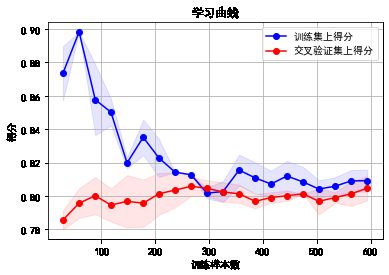
plot_learning_curve(clf, u"学习曲线", X, y)

(0.8065696844854024, 0.018258876711338634)

在实际数据上看，我们得到的learning curve没有理论推导的那么光滑哈，但是可以大致看出来，训练集和交叉验证集上的得分曲线走势还是符合预期的。

目前的曲线看来，我们的model并不处于overfitting的状态(overfitting的表现一般是训练集上得分高，而交叉验证集上要低很多，中间的gap比较大)。因此我们可以再做些feature engineering的工作，添加一些新产出的特征或者组合特征到模型中。

7 模型融合(model ensemble)

好了，终于到这一步了，我们要祭出机器学习/数据挖掘上通常最后会用到的大杀器了。恩，模型融合。

『强迫症患者』打算继续喊喊口号…
『模型融合(model ensemble)很重要！』

先解释解释，一会儿再回到我们的问题上哈。
啥叫模型融合呢，我们还是举几个例子直观理解一下好了。

大家都看过知识问答的综艺节目中，求助现场观众时候，让观众投票，最高的答案作为自己的答案的形式吧，每个人都有一个判定结果，最后我们相信答案在大多数人手里。

再通俗一点举个例子。你和你班某数学大神关系好，每次作业都『模仿』他的，于是绝大多数情况下，他做对了，你也对了。突然某一天大神脑子犯糊涂，手一抖，写错了一个数，于是…恩，你也只能跟着错了。
我们再来看看另外一个场景，你和你班5个数学大神关系都很好，每次都把他们作业拿过来，对比一下，再『自己做』，那你想想，如果哪天某大神犯糊涂了，写错了，but另外四个写对了啊，那你肯定相信另外4人的是正确答案吧？

最简单的模型融合大概就是这么个意思，比如分类问题，当我们手头上有一堆在同一份数据集上训练得到的分类器(比如logistic regression，SVM，KNN，random forest，神经网络)，那我们让他们都分别去做判定，然后对结果做投票统计，取票数最多的结果为最后结果。

bingo，问题就这么完美的解决了。

模型融合可以比较好地缓解，训练过程中产生的过拟合问题，从而对于结果的准确度提升有一定的帮助。

话说回来，回到我们现在的问题。你看，我们现在只讲了logistic regression，如果我们还想用这个融合思想去提高我们的结果，我们该怎么做呢？

既然这个时候模型没得选，那咱们就在数据上动动手脚咯。大家想想，如果模型出现过拟合现在，一定是在我们的训练上出现拟合过度造成的对吧。

那我们干脆就不要用全部的训练集，每次取训练集的一个subset，做训练，这样，我们虽然用的是同一个机器学习算法，但是得到的模型却是不一样的；同时，因为我们没有任何一份子数据集是全的，因此即使出现过拟合，也是在子训练集上出现过拟合，而不是全体数据上，这样做一个融合，可能对最后的结果有一定的帮助。对，这就是常用的Bagging。

我们用scikit-learn里面的Bagging来完成上面的思路，过程非常简单。代码如下：

from sklearn.ensemble import BaggingRegressor

train_df = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass.*|Mother|Child|Family|Title')
train_np = train_df.values

# y即Survival结果
y = train_np[:, 0]

# X即特征属性值
X = train_np[:, 1:]

# fit到BaggingRegressor之中
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
bagging_clf = BaggingRegressor(clf, n_estimators=20, max_samples=0.8, max_features=1.0, bootstrap=True, bootstrap_features=False, n_jobs=-1)
bagging_clf.fit(X, y)

test = df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass.*|Mother|Child|Family|Title')
predictions = bagging_clf.predict(test)
result = pd.DataFrame({
     'PassengerId':data_test['PassengerId'].values, 'Survived':predictions.astype(np.int32)})
result.to_csv("logistic_regression_bagging_predictions.csv", index=False)

BaggingRegressor(base_estimator=LogisticRegression(C=1.0, class_weight=None,
                                                   dual=False,
                                                   fit_intercept=True,
                                                   intercept_scaling=1,
                                                   l1_ratio=None, max_iter=100,
                                                   multi_class='warn',
                                                   n_jobs=None, penalty='l1',
                                                   random_state=None,
                                                   solver='warn', tol=1e-06,
                                                   verbose=0,
                                                   warm_start=False),
                 bootstrap=True, bootstrap_features=False, max_features=1.0,
                 max_samples=0.8, n_estimators=20, n_jobs=-1, oob_score=False,
                 random_state=None, verbose=0, warm_start=False)

pd.read_csv("logistic_regression_bagging_predictions.csv")

	PassengerId	Survived
0	892	0
1	893	0
2	894	0
3	895	0
4	896	0
...	...	...
413	1305	0
414	1306	1
415	1307	0
416	1308	0
417	1309	0

418 rows × 2 columns

然后你再Make a submission，恩，发现对结果还是有帮助的。

8 总结

文章稍微有点长，非常感谢各位耐心看到这里。
总结的部分，我就简短写几段，出现的话，很多在文中有对应的场景，大家有兴趣再回头看看。

对于任何的机器学习问题，不要一上来就追求尽善尽美，先用自己会的算法撸一个baseline的model出来，再进行后续的分析步骤，一步步提高。

在问题的结果过程中：

• 『对数据的认识太重要了！』
• 『数据中的特殊点/离群点的分析和处理太重要了！』
• 『特征工程(feature engineering)太重要了！』
• 『模型融合(model ensemble)太重要了！』

本文中用机器学习解决问题的过程大概如下图所示：