计算机图形学笔记（1）梁永栋Barsky裁剪算法

写在前面

本人刚开始学习计算机图形学小白一枚，最近刚学了梁永栋先生的经典裁剪算法，故写一篇笔记总结一下该算法，篇中如有错误之处，敬请各位指正。

基本思想

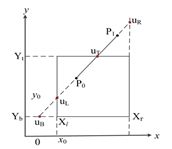
将裁剪线段及裁剪窗口均看作点集，裁剪结果即为两点集的交集，那么算法就应该从如何求交集出发。在图例中，从uB, uL和P0三点中找出最靠近P1的点P0（即求入边的终点，入边的点集的△x均大于0），然后再从uT, uR和P1中找出最靠近P0的点: uT（即求出边的起点，出边的点集的△x均小于0），最终将求出的P0，uT的u带入参数方程，就得到了P0、uT两点的坐标值，裁剪结果为线段P0 uT。

具体步骤

● 给定参数方程P0P1 : P= P0 +u*(P1 – P0)，x=x0+u△x，y=y0+u△y，△x=x1-x0 ，△y=y1-y0，设直线与裁剪窗口的4个交点为B点、L点、T点、R点。
令：
QL= -△x DL= x0-xL QR= △x DR= xR-x0
QB= -△y DB= y0-yB QT = △y DT= yT -y0
并计算参数: ui= Di / Qi (i=L,R,B,T)
● 确定始参us与终参ue : 当Qi <0时，ui为始参us；当Qi >0时，ui为终参ue；当Qi =0时，若Di <0 ,该线段不可见，舍弃该线段并结束；若Di >0 , 分析另一点的Di值。
● 最后确定交集:us=max(usx,usy,0), ue=min(uex,uey,1)，若us<=ue,则裁剪结果为区间[us, ue]，显示裁剪结果线段，否则结果为空集，则舍弃线段并结束。

图例

给定图例：

Qi =0 ,Di >0时的一种情况：

C++代码实现

#include <GL/glut.h>
#include <iostream>
/* 初始化显示窗口大小 */
GLsizei winWidth = 400, winHeight = 400;
class wcPt2D {
     
private:
	GLfloat x, y;
public:
	wcPt2D() {
     
		x = y = 0;
	}
	wcPt2D(double xd,double yd) {
     
		x = xd;
		y = yd;
	}
	void setCoords(GLfloat xCoord, GLfloat yCoord) {
     
		x = xCoord;
		y = yCoord;
	}
	GLfloat getx()const {
     
		return x;
	}
	GLfloat gety()const {
     
		return y;
	}
};
inline GLint rounds(const GLfloat a) {
     
	return GLint(a + 0.5);
}
void init() {
     
	glClearColor(1.0, 1.0, 1.0, 0.0);
	glMatrixMode(GL_PROJECTION); //将当前矩阵指定为投影矩阵 
	gluOrtho2D(-200.0, 200.0, -200.0, 200.0);
}
/*根据p、q来判断是舍弃线段还是改变交点的参数*/
GLint clipTest(GLfloat p, GLfloat q, GLfloat *u1, GLfloat *u2) {
     
	GLfloat r;
	GLint returnValue = true;
	if (p < 0.0) {
     
		r = q / p;
		if (r > *u2)
			returnValue = false;
		else if (r > *u1)
			*u1 = r;
	}
	else
		if (p > 0.0) {
     
			r = q / p;
			if (r < *u1)
				returnValue = false;
			else if (r < *u2)
				*u2 = r;
		}
		else
			if (q < 0.0)
				returnValue = false;
	return returnValue;		
}
void lineBres(int x0, int y0, int xEnd, int yEnd)
{
     
	
	glPointSize(3.0f);
	int dx = fabs(xEnd - x0);
	int dy = fabs(yEnd - y0);
	int p = 2 * dy - dy;
	int twoDy = 2 * dy, twoDyMinusDx = 2 * (dy - dx);
	int x, y;
	if (x0 > xEnd)
	{
     
		x = xEnd;
		y = yEnd;
		xEnd = x0;
	}
	else
	{
     
		x = x0;
		y = y0;
	}
	glBegin(GL_POINTS);
	glVertex2i(x, y);
	glEnd();
	while (x < xEnd)
	{
     
		x++;
		if (p < 0)
			p += twoDy;
		else
		{
     
			y++;
			p += twoDyMinusDx;
		}
		glBegin(GL_POINTS);
		glVertex2i(x, y);
		glEnd();
	}
}
//梁永栋Barsky算法主体
void lineClipLiangBarsky(wcPt2D winMin, wcPt2D winMax, wcPt2D p1, wcPt2D p2) {
     
	GLfloat u1 = 0.0, u2 = 1.0, dx = p2.getx() - p1.getx(),dy;
	GLfloat x1 = p1.getx(), y1 = p1.gety();
	GLfloat x2 = p2.getx(), y2 = p2.gety();
	if (clipTest(-dx, p1.getx() - winMin.getx(), &u1, &u2)) 
		if (clipTest(dx, winMax.getx() - p1.getx(), &u1, &u2)) {
     
			dy = p2.gety() - p1.gety();
			if (clipTest(-dy, p1.gety() - winMin.gety(), &u1, &u2) ){
     
				if (clipTest(dy, winMax.gety() - p1.gety(), &u1, &u2)) {
     
					if (u2 < 1.0) {
     
						p2.setCoords(p1.getx() + u2 * dx, p1.gety() + u2 * dy);
					}
					if (u1 > 0.0) {
     
						p1.setCoords(p1.getx() + u1 * dx, p1.gety() + u1 * dy);
					}
					glColor3f(0.0, 0.0, 0.0);
					//lineBres(rounds(p1.getx()), rounds(p1.gety()), rounds(p2.getx()), rounds(p2.gety()));
					lineBres(x1, y1, p1.getx(), p1.gety());
					lineBres(p2.getx(), p2.gety(), x2, y2);
					glColor3f(1.0, 0.0, 0.0);
					lineBres(p1.getx(), p1.gety(), p2.getx(), p2.gety());
				}
			}
			else {
     
				glColor3f(0.0, 0.0, 0.0);
				lineBres(x1, y1, x2, y2);
			}
		}
}

void displayliangBarsky(){
     
	glClear(GL_COLOR_BUFFER_BIT);
	glLineWidth(3.0);
	glColor3f(0.0, 0.0, 0.0);
	glBegin(GL_LINE_LOOP);
	   glVertex2i(100, 100);
	   glVertex2i(100, -100);
	   glVertex2i(-100, -100);
	   glVertex2i(-100, 100);
	   glEnd();
	   glPointSize(4);
    wcPt2D point1[4] = {
      {
     -100.0,-100.0},{
     100.0,100.0} ,{
     -150.0,-200.0} ,{
     200.0,120.0} };
	wcPt2D point2[4] = {
      {
     -100.0,-100.0},{
     100.0,100.0} ,{
     -150.0,-120.0} ,{
     0.0,0.0} };
	wcPt2D point3[4] = {
      {
     -100.0,-100.0},{
     100.0,100.0} ,{
     -50.0,50.0} ,{
     150.0,150.0} };
	wcPt2D point4[4] = {
      {
     -100.0,-100.0},{
     100.0,100.0} ,{
     -50.0,0.0} ,{
     60.0,50.0} };
	wcPt2D point5[4] = {
      {
     -100.0,-100.0},{
     100.0,100.0} ,{
     -170.0,-200.0} ,{
     200.0,-120.0} };
	lineClipLiangBarsky(point1[0], point1[1], point1[2], point1[3]);
	lineClipLiangBarsky(point2[0], point2[1], point2[2], point2[3]);
	lineClipLiangBarsky(point3[0], point3[1], point3[2], point3[3]);
	lineClipLiangBarsky(point4[0], point4[1], point4[2], point4[3]);
	lineClipLiangBarsky(point5[0], point5[1], point5[2], point5[3]);
	glFlush();
}
void main(int argc, char ** argv)
{
     
	glutInit(&argc, argv);  // 初始化GLUT库 
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	//单缓冲，建立RGB模式窗口 
	glutInitWindowPosition(50, 100);
	glutInitWindowSize(winWidth, winHeight);
	glutCreateWindow("梁永栋-Barsky算法");
	init();
	glutDisplayFunc(displayliangBarsky);
	glutMainLoop();
}

运行结果

参考书籍

Donald Hearn M.Pauline Baker Warren R.Carithers《计算机图形学 Computer Graphics with OpenGL 》[M].第四版.北京：电子工业出版社，2014年