计算机图形学--多边形扫瞄转换与区域填充实现
原创作品,出自 “晓风残月xj” 博客,欢迎转载,转载时请务必注明出处(http://blog.csdn.net/xiaofengcanyuexj)。
由于各种原因,可能存在诸多不足,欢迎斧正!
多边形的扫描转换与区域填充。
我选了两个算法实现:
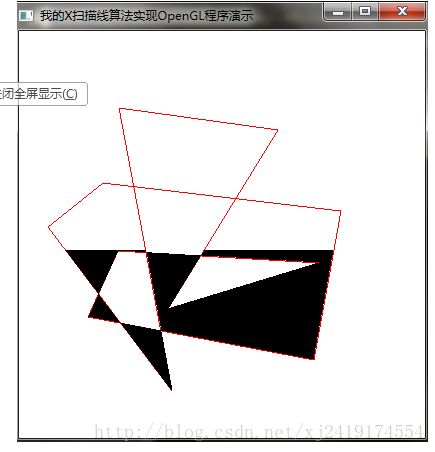
1.多边形扫描转换的X轴扫描线算法
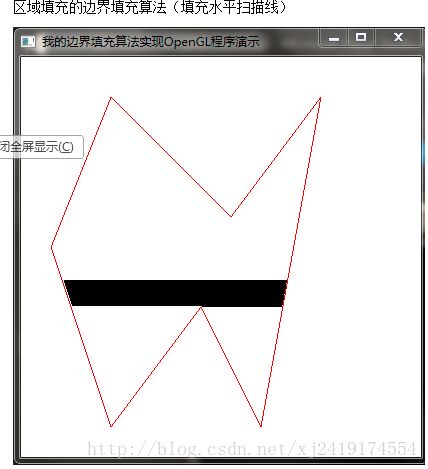
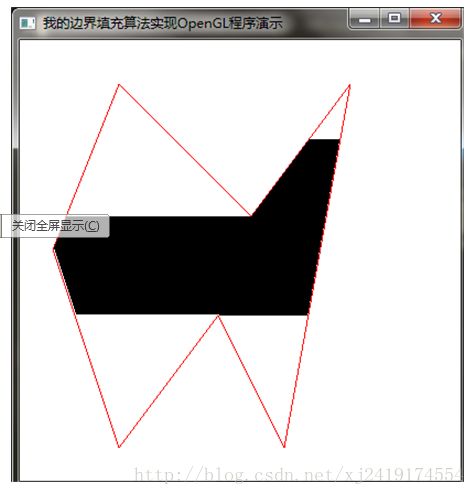
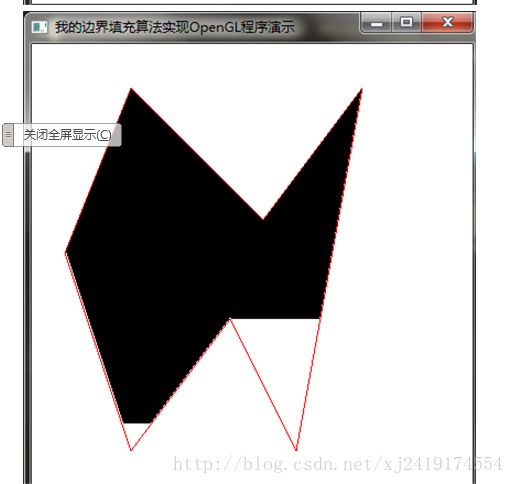
2.区域填充的边界填充算法(填充水平扫描线)。
一、设计思想
多边形扫描转换的X轴扫描线算法
基本思想:如下图所示,按扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的所有像素。
算法步骤:
(1)确定多边形所占有的最大扫描线数,得到多边形顶点的最小和最大y值(ymin和ymax)。
(2)从y=ymin到y=ymax,每次用一条扫描线进行填充。填充过程可分为四个步骤:
a.求交:计算扫描线与多边形各边的交点;
b.排序:把所有交点按照递增顺序进行排序;
c.交点配对:交点两两配对,表示扫描线与多边形的一个相交区间;
d.区间填色:将相交区间内的像素置成不同于背景色的填充色。
存在问题:当扫描线与多边形顶点相交时,交点的取舍问题。如下图所示,在扫描线y=1,y=5和y=7时,扫描线过多边形的顶点,若不加以处理,交点配对时会发生错误。
与多边形相交的交点的处理
解决方法:当扫描线与多边形的顶点相交时,若共享顶点的两条边分别落在扫描线的两边,交点只算一个;若共享顶点的两条边在扫描线的同一边,这时交点作为零个或两个。实际处理时,只要检查顶点的两条边的另外两个端点的Y值,两个Y值中大于交点Y值的个数是0,1,2,来决定取0,1,2个交点。
区域填充的边界填充算法(填充水平扫描线)
通过沿扫描线填充水平像素段,来代替处理4-邻接点和8-邻接点。
原理:扫描线通过在任意不间断扫描线区间中只取一个种子像素的方法使堆栈的尺寸极小化。不间断区间是指在一条扫描线上的一组相邻像素。
沿扫描线填充水平像素段示意图
基本过程:当给定种子点时,首先填充种子点所在的扫描线上的位于给定区域的一个区段,然后确定与这一区段相通的上下两条扫描线上位于给定区域内的区段,并依次保存下来。反复这个过程,直到填充结束。
扫描线填充水平像素段的4-连通边界填充算法步骤:
种子像素入栈;当栈非空时作如下三步操作:
(1)栈顶像素出栈;
(2)填充出栈像素所在扫描行的连续像素段,直到遇到边界像素为止,即每出栈一个像素,就对包含该像素的整个扫描线区间进行填充;
(3)在区间中检查与当前扫描线相邻的上下两条扫描线的有关像素是否全为边界像素或已填充的像素,若存在非边界、未填充边界的像素,则把每一区间的最右像素取作种子像素入栈。
二、实验特色
对于多边形扫描转换的X轴扫描线算法,我的程序结合了鼠标响应,实现了在窗口中用鼠标打点,顺次首尾相接连成直线后构成了一个多边形。然后动态演示X轴扫描线算法的实现过程。生动、直观并且可以多次绘制。
对于区域填充的边界填充算法(填充水平扫描线),我的程序可以在控制台下输入多边形的顶点,然后动态演示填充过程。
三、调试分析
首先我是验证课本上的那个多边形,可是总是不能显示出来,后来发现是图形太小,于是我所有顶点都*30,图形得以显示
四、截图
#include
#include
#include
#include
#include
#include
using namespace std;
int winWidth=400, winHeight=400;
const int INF=1<<30;
const int MAXN=400*400;
struct point
{
int x,y;
}Point[MAXN];
int numberpoint;
int MaxY,MinY;
vectorVec[MAXN]; //Vec[i]存放形如(x,i)的交点
bool Hash[MAXN]; //辅助判断顶点算几次
int id; //当前处理到的Vec[MAXN]d的最大下表
/*******************************************************
*函数名XScanAlgorithm
*无参数
*X扫描转换算法的实现,选择水平扫描线与多边形的交点
********************************************************/
void XScanAlgorithm()
{
for(int index=0,y=MinY;y<=MaxY;y++,index++)
{
memset(Hash,false,sizeof(Hash));
for(int i=0;i0)
{
Vec[index].push_back(Point[i].x);
}
}
if((Point[i].yy)||(Point[i].y>y&&Point[(i+1)%numberpoint].yMaxY-MinY)
return ;
Display();
id++;
glutTimerFunc(10,Delay,pa);
}
/*******************************************************
*函数名ChangeSize
*无参数
*窗口发生变化时完成初始化
********************************************************/
void ChangeSize(int w, int h)
{
winWidth=w;winHeight=h;
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0,winWidth,0.0,winHeight);
}
/*******************************************************
*函数名MousePlot
*鼠标按键、按键方式、对应x,y的坐标
*鼠标响应函数,左键画圆同时指定圆心,右键画直线同时指定直线的两个端点
********************************************************/
void MyMouse(GLint button, GLint action, GLint xMouse, GLint yMouse)
{
if(button==GLUT_LEFT_BUTTON&&action==GLUT_DOWN)
{
Point[numberpoint].x=xMouse;Point[numberpoint].y=winHeight-yMouse;
if(Point[numberpoint].y>MaxY)
{
MaxY=Point[numberpoint].y;
}
if(Point[numberpoint].y #include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
int winWidth=400, winHeight=400;
const int INF=1<<30;
const int MAXN=400*400;
struct point
{
int x,y;
}Point[MAXN]; //存储多边形的顶点
stackMyStack;
int numberpoint;
int MaxY,MinY;
vectorVec[MAXN];
bool Hash[1000][1000];//判断是否要填充
struct fillline
{
point start,end;
}; //待填充的扫描线
vectorFill;
/*******************************************************
*函数名XScanAlgorithm
*无参数
*X扫描转换算法的实现,选择水平扫描线与多边形的交点
********************************************************/
void XScanAlgorithm()
{
memset(Hash,false,sizeof(Hash));
Fill.clear();
for(int i=0;i0)
{
Vec[id].push_back(Point[i].x);
}
}
if((Point[i].yy)||(Point[i].y>y&&Point[(i+1)%numberpoint].y>numberpoint;
for(int i=0;i>Point[i].x>>Point[i].y;
Point[i].x*=30;Point[i].y*=30;
if(Point[i].y>MaxY)
{
MaxY=Point[i].y;
}
if(Point[i].y400-10)break;
if(Hash[tpoint.y][i])break;
Hash[tpoint.y][i]=true;
}
int right=i-1;
tline.start.y=tpoint.y; tline.start.x=right;//右边的点
for(i=tpoint.x-1;;i--)
{
if(i<10)break;
if(Hash[tpoint.y][i])break;
Hash[tpoint.y][i]=true;
}
int left=i+1;
tline.end.y=tpoint.y; tline.end.x=left;
if(!(tline.end.y==tline.start.y&&tline.end.x==tline.start.x))
Fill.push_back(tline); //左边的点
point a;
bool flag;
if(tpoint.y!=MinY)//存在一条位于下方的扫描线
{
int tmp=tpoint.y-1;
flag=false;
for(i=left;i