Matlab降维工具箱drtoolbox使用演示
学习目标:
matlab降维工具包
提取码:m6dj
里面含有两个压缩包,解压后的文件含有:
drtoolbox(1)有工具箱的使用说明pdf和工具箱的下载包:
matlab的数据是接下来演示的数据集:

学习内容:
1、 数据导入
解压后有四个MATLAB Data,直接双击导入Matlbel中,其中trainX对应unnamed,trainY对应unnamed1,testX对应unname2,testY对应unname3.这里是一个分类数据集(像trainY就是四类1,2,3,4),并且是高位数据集(trainX就是152个样本量,但是有153个属性)。


2、 pdf说明书
当时学习这个工具箱的时候找到了这本书《An Introduction to Dimensionality Reduction Using Matlab》,里面详细说明了工具箱包含的降维方法的理论原理并且有实际例子,非常适合小白学习:

3、 方法演示
1.利用intrinsic_dim(X, 'MLE')来查看此方法建议你降维至第几维
X = unnamed;%数据每个样本为一行。
labels = unnamed1;
no_dims = round(intrinsic_dim(X, 'MLE'));
disp(['MLE estimate of intrinsic dimensionality: ' num2str(no_dims)]);
这里建议降维至2维。
2.选用合适的方法
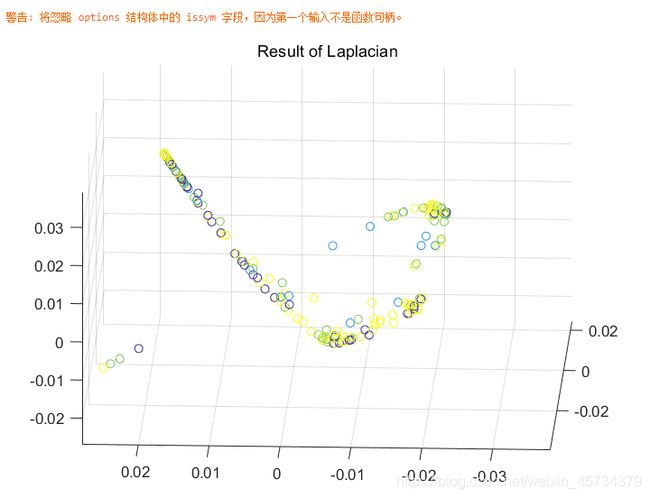
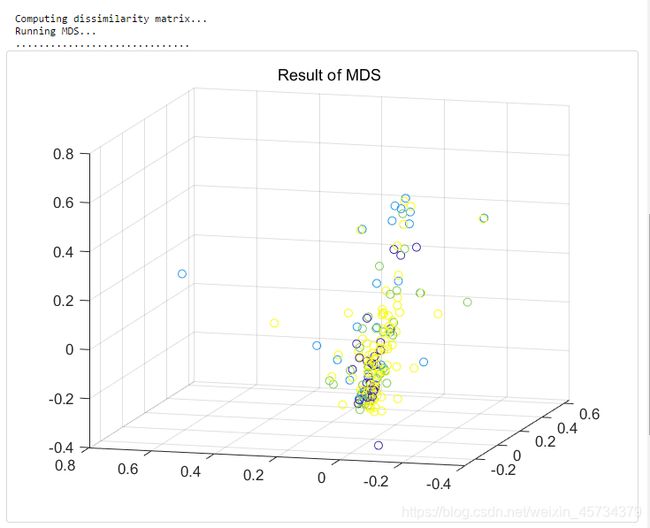
不同的降维方法适用于不同的数据集,详细学习请见《An Introduction to Dimensionality Reduction Using Matlab》,下面演示Laplacian降维和MDS降维,它们都是降至3维的演示:
X = unnamed;%数据每个样本为一行。
labels = unnamed1;
no_dims = round(intrinsic_dim(X, 'MLE'));
%disp(['MLE estimate of intrinsic dimensionality: ' num2str(no_dims)]);
%[mappedX1, mapping] = compute_mapping(X, 'Laplacian', no_dims);
[mappedX3, mapping3] = compute_mapping(X, 'Laplacian',3);
colormap(jet)
figure, scatter3(mappedX3(:,1), mappedX3(:,2), mappedX3(:,3),30, labels);
%figure, scatter(mappedX1(:,1), mappedX1(:,2),30, labels);
%xlim([-0.3,0.2]);
%ylim([-0.2,0.2]);
%zlim([-0.04,0.022]);
title('Result of Laplacian');
X = unnamed;%数据每个样本为一行。
labels = unnamed1;
no_dims = round(intrinsic_dim(X, 'MLE'));
%disp(['MLE estimate of intrinsic dimensionality: ' num2str(no_dims)]);
[mappedX1, mapping] = compute_mapping(X, 'MDS', 3);
%colormap(jet)
figure, scatter3(mappedX1(:,1), mappedX1(:,2), mappedX1(:,3),30, labels);
%figure, scatter(mappedX1(:,1), mappedX1(:,2),30, labels);
%xlim([-0.3,0.2]);
%ylim([-0.3,0.2]);
%zlim([-0.4,0.22]);
title('Result of MDS');
3.数据导出
数据便是上述代码中[mappedX1, mapping] = compute_mapping(X, 'MDS', 3);的mappedX1.
学习总结
这个降维虽然好用,但是主观性非常强,本次演示的数据其实降维效果不好,最后进一步做分类器的时候效果很差,尝试尝试各种降维方式也是受益匪浅,但是还需慎用。