第10章 PCA/SVM(人脸识别)
sklearn.decomposition.PCA
Linear dimensionality reduction using Singular Value Decomposition of the data to project it to a lower dimensional space.
PCA 用于对一组连续正交分量中的多变量数据集进行方差最大方向的分解。 在 scikit-learn 中, PCA 被实现为一个变换对象, 通过 fit 方法可以降维成 n 个成分, 并且可以将新的数据投影(project, 亦可理解为分解)到这些成分中。
人脸数据集来自英国剑桥AT&T实验室,包含40位人员照片,每个人10张。sklearn.datasets自带此数据集。下载链接:The Database of Faces_AT&T
import matplotlib.pyplot as plt
import numpy as np
import time
import logging
from sklearn.datasets import fetch_olivetti_faces
logging.basicConfig(level=logging.INFO, format='%(asctime)s %(message)s')
data_home=r'C:\Users\Qiuyi\Desktop\scikit-learn code\code\datasets\olivetti_py3'
logging.info('Start to load dataset')
faces = fetch_olivetti_faces(data_home=data_home)
logging.info('Done with load dataset')
2018-12-19 23:04:40,449 Start to load dataset
2018-12-19 23:04:40,484 Done with load dataset
logging模块使用教程
默认情况下,logging模块将日志打印到屏幕上(stdout),日志级别为WARNING(即只有日志级别高于WARNING的日志信息才会输出)。
| 日志级别 | 何时使用 |
|---|---|
| DEBUG | 详细信息,典型地调试问题时会感兴趣。 |
| INFO | 证明事情按预期工作。 |
| WARNING | 表明发生了一些意外,或者不久的将来会发生问题(如‘磁盘满了’)。软件还是在正常工作。 |
| ERROR | 由于更严重的问题,软件已不能执行一些功能了。 |
| CRITICAL | 严重错误,表明软件已不能继续运行了。 |
basicConfig关键字参数
format handler使用指明的格式化字符串。
%(asctime)s 打印日志的时间
%(message)s 打印日志信息
sklearn.datasets.fetch_olivetti_faces()
如果电脑里没有数据集也没关系,fetch_olivetti_faces()会帮你自动从网上下载并保存在get_data_home()获得的地址中。
return
- data : numpy array of shape (400, 4096)
Each row corresponds to a ravelled face image of original size 64 x 64 pixels. - images : numpy array of shape (400, 64, 64)
Each row is a face image corresponding to one of the 40 subjects of the dataset. - target : numpy array of shape (400, )
Labels associated to each face image. Those labels are ranging from 0-39 and correspond to the Subject IDs. - DESCR : string
Description of the modified Olivetti Faces Dataset.
2018-12-19 23:34:27,591 Start to load dataset
downloading Olivetti faces from https://ndownloader.figshare.com/files/5976027 to C:\Users\Qiuyi\scikit_learn_data
2018-12-19 23:35:11,625 Done with load dataset
显示数据的概要信息:
X = faces.data
y = faces.target
targets = np.unique(faces.target)
target_names = np.array(["c%d" % t for t in targets])
n_targets = target_names.shape[0]
n_samples, h, w = faces.images.shape
print('Sample count: {}\nTarget count: {}'.format(n_samples, n_targets))
print('Image size: {}x{}\nDataset shape: {}\n'.format(w, h, X.shape))
Sample count: 400
Target count: 40
Image size: 64x64
Dataset shape: (400, 4096)
观察人脸图片,随机选择n_row * n_col个人,并自动调节窗口尺寸:
def plot_gallery(images, titles, h, w, n_row=2, n_col=5):
"""显示图片阵列"""
plt.figure(figsize=(2 * n_col, 2.2 * n_row), dpi=144)
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.01)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
plt.title(titles[i])
plt.axis('off')
n_row = 2
n_col = 6
sample_images = None
sample_titles = []
for i in range(n_targets):
people_images = X[y==i]
people_sample_index = np.random.randint(0, people_images.shape[0], 1)
people_sample_image = people_images[people_sample_index, :]
if sample_images is not None:
sample_images = np.concatenate((sample_images, people_sample_image), axis=0)
else:
sample_images = people_sample_image
sample_titles.append(target_names[i])
plot_gallery(sample_images, sample_titles, h, w, n_row, n_col)
划分训练集和测试集,并用SVC训练,预测:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=4)
from sklearn.svm import SVC
start = time.clock()
print('Fitting train datasets ...')
clf = SVC(class_weight='balanced')
clf.fit(X_train, y_train)
print('Done in {0:.2f}s'.format(time.clock()-start))
Fitting train datasets …
Done in 1.21s
start = time.clock()
print("Predicting test dataset ...")
y_pred = clf.predict(X_test)
print('Done in {0:.2f}s'.format(time.clock()-start))
Predicting test dataset …
Done in 0.17s
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred, labels=range(n_targets))
print("confusion matrix:\n")
np.set_printoptions(threshold=np.nan)
#为了确保完整的输出cm数组的内容,40x40
print(cm)
confusion matrix:
[[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2]]
混淆矩阵理想的输出,是对角线上有数字,其他地方都没有数字。
再看看classification_report的结果:
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred, target_names=target_names))
precision recall f1-score support
c0 0.00 0.00 0.00 1
c1 0.00 0.00 0.00 3
c2 0.00 0.00 0.00 2
c3 0.00 0.00 0.00 1
c4 0.00 0.00 0.00 1
c5 0.00 0.00 0.00 1
c6 0.00 0.00 0.00 4
c7 0.00 0.00 0.00 2
c8 0.00 0.00 0.00 4
c9 0.00 0.00 0.00 2
c10 0.00 0.00 0.00 1
c11 0.00 0.00 0.00 0
c12 0.00 0.00 0.00 4
c13 0.00 0.00 0.00 4
c14 0.00 0.00 0.00 1
c15 0.00 0.00 0.00 1
c16 0.00 0.00 0.00 3
c17 0.00 0.00 0.00 2
c18 0.00 0.00 0.00 2
c19 0.00 0.00 0.00 2
c20 0.00 0.00 0.00 1
c21 0.00 0.00 0.00 2
c22 0.00 0.00 0.00 3
c23 0.00 0.00 0.00 2
c24 0.00 0.00 0.00 3
c25 0.00 0.00 0.00 3
c26 0.00 0.00 0.00 2
c27 0.00 0.00 0.00 2
c28 0.00 0.00 0.00 0
c29 0.00 0.00 0.00 2
c30 0.00 0.00 0.00 2
c31 0.00 0.00 0.00 3
c32 0.00 0.00 0.00 2
c33 0.00 0.00 0.00 2
c34 0.00 0.00 0.00 0
c35 0.00 0.00 0.00 2
c36 0.00 0.00 0.00 3
c37 0.00 0.00 0.00 1
c38 0.00 0.00 0.00 2
c39 0.00 0.00 0.00 2
avg / total 0.00 0.00 0.00 80
C:\Python36\lib\site-packages\sklearn\metrics\classification.py:1135: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples.
‘precision’, ‘predicted’, average, warn_for)
C:\Python36\lib\site-packages\sklearn\metrics\classification.py:1137: UndefinedMetricWarning: Recall and F-score are ill-defined and being set to 0.0 in labels with no true samples.
‘recall’, ‘true’, average, warn_for)
查准率、召回率、F1 Score全为0,可见直接预测效果非常差。
因为把每个像素都作为输入特征来处理,使数据噪声太严重。特征有4096个,比400个数据集数量还多。而且还要分出20%作为测试数据集。
因此需要使用数据降维:
from sklearn.decomposition import PCA
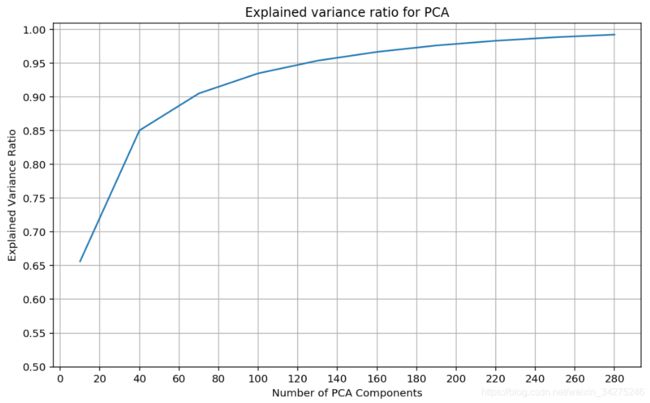
print("Exploring explained variance ratio for dataset ...")
candidate_components = range(10, 300, 30) #(10,40,70,100,...,250,280)
explained_ratios = []
start = time.clock()
for c in candidate_components:
pca = PCA(n_components=c)
X_pca = pca.fit_transform(X)
explained_ratios.append(np.sum(pca.explained_variance_ratio_))
print('Done in {0:.2f}s'.format(time.clock()-start))
Exploring explained variance ratio for dataset …
Done in 8.13s
PCA(n_components) : int, float, None or string
Number of components to keep. if n_components is not set all components are kept:
n_components == min(n_samples, n_features)
explained_variance_ratio_ : array, shape (n_components,)
经PCA处理后的数据还原率。
Percentage of variance explained by each of the selected components.
plt.figure(figsize=(10, 6), dpi=144)
plt.grid()
plt.plot(candidate_components, explained_ratios)
plt.xlabel('Number of PCA Components')
plt.ylabel('Explained Variance Ratio')
plt.title('Explained variance ratio for PCA')
plt.yticks(np.arange(0.5, 1.05, .05))
plt.xticks(np.arange(0, 300, 20));
取出之前挑选的人脸图片中的前五个,利用 pca.inverse_transform() 可视化不同 n_components 下图片的还原率:
def title_prefix(prefix, title):
return "{}: {}".format(prefix, title)
n_row = 1
n_col = 5
sample_images = sample_images[0:5]
sample_titles = sample_titles[0:5]
plotting_images = sample_images
plotting_titles = [title_prefix('orig', t) for t in sample_titles] #原始图片title
candidate_components = [140, 75, 37, 19, 8]
for c in candidate_components:
print("Fitting and projecting on PCA(n_components={}) ...".format(c))
start = time.clock()
pca = PCA(n_components=c)
pca.fit(X)
X_sample_pca = pca.transform(sample_images) #原始图片
X_sample_inv = pca.inverse_transform(X_sample_pca) #还原后的图片
plotting_images = np.concatenate((plotting_images, X_sample_inv), axis=0)
sample_title_pca = [title_prefix('{}'.format(c), t) for t in sample_titles]
plotting_titles = np.concatenate((plotting_titles, sample_title_pca), axis=0)
#测试图片title
print("Done in {0:.2f}s".format(time.clock() - start))
print("Plotting sample image with different number of PCA conpoments ...")
plot_gallery(plotting_images, plotting_titles, h, w,
n_row * (len(candidate_components) + 1), n_col)
Fitting and projecting on PCA(n_components=140) …
Done in 0.82s
Fitting and projecting on PCA(n_components=75) …
Done in 0.40s
Fitting and projecting on PCA(n_components=37) …
Done in 0.15s
Fitting and projecting on PCA(n_components=19) …
Done in 0.12s
Fitting and projecting on PCA(n_components=8) …
Done in 0.09s
Plotting sample image with different number of PCA conpoments …

可见即使在 n_components=8时,图片依然能比较清楚地反映出人物的脸部特征轮廓。
选择还原率在95%时的 n_components,即140。
n_components = 140
print("Fitting PCA by using training data ...")
start = time.clock()
pca = PCA(n_components=n_components, svd_solver='randomized', whiten=True).fit(X_train)
print("Done in {0:.2f}s".format(time.clock() - start))
print("Projecting input data for PCA ...")
start = time.clock()
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("Done in {0:.2f}s".format(time.clock() - start))
Fitting PCA by using training data …
Done in 0.87s
Projecting input data for PCA …
Done in 0.02s
GridSearchCV
用于系统地遍历多种参数组合,通过交叉验证确定最佳效果参数。
- estimator —— 分类器
- param_grid —— 字典或列表
- scoring : 评分函数,例如 scoring=‘roc_auc’,默认None
- n_jobs : 并行任务个数,int, default=1
- cv : int, 交叉验证,默认3
- verbose:int:日志冗长度,0:不输出训练过程,1:偶尔输出,>1:对每个子模型都输出。
return:
- best_params_ : dict
Parameter setting that gave the best results on the hold out data. - best_estimator_ : estimator or dict
Estimator that was chosen by the search
sklearn.model_selection.GridSearchCV
Exhaustive search over specified parameter values for an estimator.
from sklearn.model_selection import GridSearchCV
print("Searching the best parameters for SVC ...")
param_grid = {
'C': [1, 5, 10, 50, 100],
'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01]}
clf = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'),
param_grid, verbose=2, n_jobs=4)
clf = clf.fit(X_train_pca, y_train)
print("Best parameters found by grid search:")
print(clf.best_params_)
Searching the best parameters for SVC …
Fitting 3 folds for each of 25 candidates, totalling 75 fits
[Parallel(n_jobs=4)]: Done 36 tasks | elapsed: 2.2s
Best parameters found by grid search:
{‘C’: 10, ‘gamma’: 0.001}
[Parallel(n_jobs=4)]: Done 75 out of 75 | elapsed: 2.8s finished
直接用 GridSearchCV 返回的 best_estimator_ 进行预测:
start = time.clock()
print("Predict test dataset ...")
y_pred = clf.best_estimator_.predict(X_test_pca)
cm = confusion_matrix(y_test, y_pred, labels=range(n_targets))
print("Done in {0:.2f}.\n".format(time.clock()-start))
print("confusion matrix:")
np.set_printoptions(threshold=np.nan)
print(cm)
Predict test dataset …
Done in 0.01.
confusion matrix:
[[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2]]
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 0.50 1.00 0.67 1
1 1.00 0.67 0.80 3
2 1.00 0.50 0.67 2
3 1.00 1.00 1.00 1
4 1.00 1.00 1.00 1
5 1.00 1.00 1.00 1
6 1.00 0.75 0.86 4
7 1.00 1.00 1.00 2
8 1.00 1.00 1.00 4
9 1.00 1.00 1.00 2
10 1.00 1.00 1.00 1
12 1.00 1.00 1.00 4
13 1.00 1.00 1.00 4
14 1.00 1.00 1.00 1
15 1.00 1.00 1.00 1
16 0.75 1.00 0.86 3
17 1.00 1.00 1.00 2
18 1.00 1.00 1.00 2
19 1.00 1.00 1.00 2
20 1.00 1.00 1.00 1
21 1.00 1.00 1.00 2
22 0.75 1.00 0.86 3
23 1.00 1.00 1.00 2
24 1.00 1.00 1.00 3
25 0.67 0.67 0.67 3
26 1.00 1.00 1.00 2
27 1.00 1.00 1.00 2
29 1.00 1.00 1.00 2
30 1.00 1.00 1.00 2
31 1.00 1.00 1.00 3
32 1.00 1.00 1.00 2
33 1.00 1.00 1.00 2
35 1.00 1.00 1.00 2
36 1.00 1.00 1.00 3
37 1.00 1.00 1.00 1
38 1.00 1.00 1.00 2
39 1.00 1.00 1.00 2
avg / total 0.96 0.95 0.95 80
参考网址:
张洋
PCA的数学原理
孟岩
理解矩阵(一)
理解矩阵(二)
理解矩阵(三)