机器学习入门算法讲解:梯度下降、KNN、逻辑斯特回归、SVM，决策树，朴素贝叶斯

机器学习入门算法讲解:梯度下降、KNN、逻辑斯特回归、SVM，决策树，朴素贝叶斯

**引言：**2015-2020是机器学习飞速发展的几年，指纹识别，人脸识别一改传统的模板匹配算法，投入机器学习的怀抱，但许多机器学习算法都不需要我们手写代码，利用python工具可以直接在库中调用，本人结合一些数学讲解（高中水平就行），通过代码演示，给大家讲几个基础的算法供大家入门机器学习。
在介绍之前，我先给大家普及下人工智能，机器学习，神经网络，深度学习的概念，如下图：

1956年提出的’人工智能‘，是一个领域，包括推理，联想，学习等多种技术，而机器学习是在20世纪八九十年代发展起来的一个分支，主要研究如何让机器具有学习能力，越学越厉害那种。
神经网络，也叫人工神经网络，虽然提出时间比机器学习还早，但现在多指基于人工神经网络的机器学习算法，它的关键技术是反向传播算法，。深度学习指深度神经网络下的机器学习，什么叫深度呢，一般认为三层以上的神经网络就叫深度神经网络了。
为什么深度学习现在这么火呢？当然是因为人家牛逼，牛逼之处在于我们不需要关心信号中的特征，深度网络会自动学习到一种最优模式，从而使模型可以精确输出预测值。它克服了
手工特征提取这个最大的流程瓶颈。比如如何辨别人和猫，以特征提取的思想来看，人耳朵圆，鼻子大，我们将这些特征告诉机器，它才能学习并辨别人和猫，但深度学习，只要你傻瓜的扔进去一组数据，它就会自动学习特征。对时序信号同样如此。
以下步入正题：

梯度下降（Gradient Descent）

我以一个线性方程的拟合给大家介绍梯度下降，利用python生成下面一组数据：

import matplotlib.pyplot as plt
import numpy as np
X=np.arange(0,100,1)
rand=np.random.randn(100)#正态分布随机数，均值0 方差1
b=10
w=1
y=w*X+rand+b
plt.xlabel("x")
plt.ylabel("y")
plt.scatter(X,y,s=2)

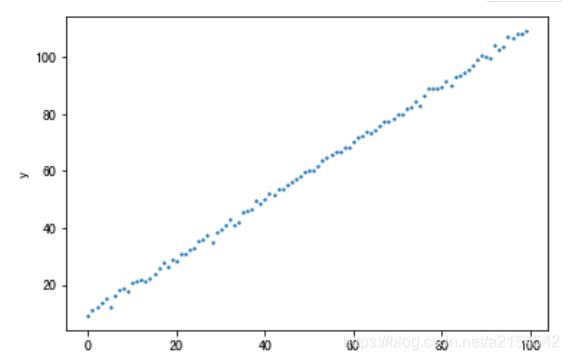
高中大家都学过最小二乘法，对线性函数进行拟合，为了拟合上图的图像，我们建立方程y=kx+b,如何判断拟合的准确程度呢，建立误差函数

之后我们观察图像，发现k应该是在[0，2]区间中，b是在[5，15]区间中，我们利用暴力穷举法对方程进行拟合：

def cost(x,y,k1,k2):
    predict=k1*x+k2
    cost=sum((predict-y)**2)/90
    return cost
Xs=np.arange(0,2,0.02)
Ys=np.arange(5,15,0.1)
Zs=np.zeros([100,100])
Xs,Ys=np.meshgrid(Xs,Ys)
k,b=[],[]
lost=[]
for i in range(100):
    for j in range(100):
        k.append(0.02*i)
        b.append(0.1*j)
        lost.append(cost(X,y,0.02*i,0.1*j))
index=np.array(lost).argmin()
print(k[index],b[index],lost[index])

from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import LinearLocator,FormatStrFormatter
import matplotlib.pyplot as plt
from matplotlib import cm
%matplotlib inline
fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.view_init(0,160)
ax.scatter(w1,w2,lost,s=10,alpha=0.02,linestyle='-')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('error')
ax.scatter(6.4,9.8,zs=cost(X_train,6.4,9.8),s=100,color='red')

输出如下

由于b值过小，可见对结果影响并不大，一般情况下该图形为碗的性质，有且仅有一个极小值点。
接着我们看梯度下降法：求梯度，类似于求导，求k和b在该图像上的偏导数，程序实现较为简单：

def Gradient(X,y,k1,k2):
    gradk1=(cost(X,y,k1+0.01,k2)-cost(X,y,k1,k2))/0.01
    gradk2=(cost(X,y,k1,k2+0.01)-cost(X,y,k1,k2))/0.01 
    return (gradk1,gradk2)
error=[]
def GradientDesent():
    k1,k2=0,0
    epoch=1000

    learning_rate=0.0001
    learning_rate2=0.01
    for i in range(epoch):
        k1=k1-learning_rate*Gradient(X,y,k1,k2)[0]
        k2=k2-learning_rate2*Gradient(X,y,k1,k2)[1]
        error.append(cost(X,y,k1,k2))#保存误差用于绘图
    print("经过梯度下降后k=%.2f b=%.2f error=%.2f"%(k1,k2,cost(X,y,k1,k2)))

GradientDesent()
最终输出为
经过梯度下降后k=0.98 b=11.13 error=1.44

由于在梯度的方向下，函数变化最快，故我们求出梯度后让参数在这个方向变化，即可快速找到函数最小值。但经过2000次循环后的数据并不是真正的极小值，我们利用如下方法找到error极小值。

plt.plot(error)
plt.xlabel("epochs")
plt.ylabel("error")
A=error.index(min(error))+1 #寻找最小值下标
print(A)

最后结果为469，即469个循环后效果才是最好的，最终输出为
经过梯度下降后k=0.99 b=10.34 error=1.16

以上就是一个基础的的梯度下降算法，也掺杂了一些模型训练的知识，其中error代表模型损失函数，learning_rate代表学习率，循环次数epoch即训练轮数

待更新。。。