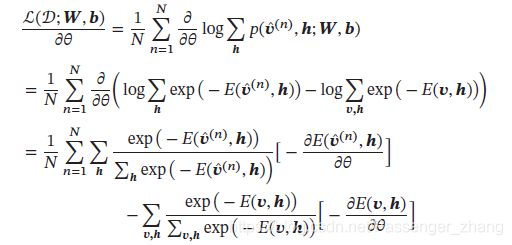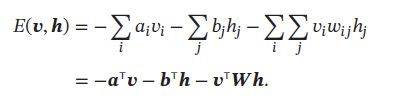《神经网络与深度学习》-深度信念网络
深度信念网络
-
- 1. 玻尔兹曼机
-
- 1.1 生成模型
- 1.2 能量最小化与模拟退火
- 1.3 参数学习
- 2. 受限玻尔兹曼机
-
- 2.1 生成模型
- 2.2 参数学习
-
- 2.2.1 对比散度学习算法
- 2.3 受限玻尔兹曼机的类型
- 3. 深度信念网络
-
- 3.1 生成模型
- 3.2 参数学习
-
- 3.2.1 逐层预训练
- 3.2.1 精调
对于复杂的数据分布,通常只能观测到有限的局部特征,且含有噪声,如要对这个数据分布进行建模,要挖掘可观测变量之间的依赖关系,以及可观测变量背后隐藏的内部表示
本文介绍可有效学习变量之间复杂依赖关系的概率图模型( 深度信念网络)以及两基础模型( 玻尔兹曼机、 受限玻尔兹曼机)。深度信念网络含很多隐变量,可有效学习数据的内部特征表示,也可以作为一种非线性降维方法,学到的特征包含了数据的更高级、有价值的信息,故十分有助于后续的分类和回归任务。
玻尔兹曼机、深度信念网络都是生成模型,借助隐变量来描述复杂的数据分布,共同问题都是推断和学习问题,常通过MCMC方法来近似估计。
1. 玻尔兹曼机
玻尔兹曼机(Boltzmann Machine)可看做一个随机动力系统(Stochastic Dynamical System)。每个变量转态以一定概率收到其他变量影响,可用概率无向图模型来描述,一个具有K个节点(变量)的玻尔兹曼机满足三个性质:
- 每个随便变量是二值的,所有随机变量可用 X ∈ { 0 , 1 } K X\in\{0,1\}^K X∈{ 0,1}K表示,其中可观测变量表示为 V \pmb{V} VVV,隐变量表示为 H \pmb{H} HHH
- 所有节点之间是全连接的,每个变量 X i X_i Xi的取值依赖于所有其他变量 X i \pmb{X}_{\\i} XXXi
- 每两个变量之间的相互影响是 ( X i → X j , X j → X i ) (X_i \to X_j ,X_j \to X_i) (Xi→Xj,Xj→Xi)对称的
包含3个可观测变量和3个隐变量的玻尔兹曼机图示:

随机向量 X \pmb{X} XXX的联合概率密度由玻尔兹曼分布得到,即:

其中 Z 为配分函数,T表示温度,能量函数 E ( x ) E(\pmb{x}) E(xxx)的定义为:

其中 w i j w_{ij} wij是两个变量 x i x_i xi和 x j x_j xj之间的连接权重, x i ∈ { 0 , 1 } x_i \in \{0,1\} xi∈{ 0,1}表示状态, b i b_i bi是变量 x i x_i xi的偏置。
如果 X i X_i Xi和 X j X_j Xj的取值都为1时,一个正的权重 w i j > 0 w_{ij}>0 wij>0会使得玻尔兹曼机的能量下降,发生的概率变大;相反,一负的权重会使得玻尔兹曼机的能量上升,发生的概率变小。故如果令玻尔兹曼机中每个变量 X i X_i Xi代表一个基本假设, 取值为1或0分别表示模型接受或拒绝该假设,那么变量之间连接的权重代表了两个假设之间的弱约束关系。连接权重可正可负的实数:正的权重表示两个假设可以相互支持,或一个假设被接受另一个也很可能被接受,相反,负的权重表示两个假设不能同时被接受。
玻尔兹曼机可用来解决两类问题:
- 搜索问题:当给定变量之间的连接权重时,需找到一组二值向量,使得整个网络的能量最低
- 学习问题:当给定变量的多组观测时,学习网络的最优权重
1.1 生成模型
在玻尔兹曼机中,配分函数Z通常难以计算,因此,联合概率分布 p ( x ) p(\pmb{x}) p(xxx)一般通过MCMC方法来近似,生成一组服从 p ( x ) p(\pmb{x}) p(xxx)分布的样本。下面介绍基于吉布斯采样的样本生成方法
全条件概率 吉布斯采样需要计算每个变量 X i X_i Xi 的全条件概率 p ( x i ∣ x i ) p(x_i|\pmb{x}_{\\i}) p(xi∣xxxi),其中 x i \pmb{x}_{\\i} xxxi表示除变量 X i X_i Xi 外其他变量的取值

吉布斯采样 玻尔兹曼机的吉布斯采样过程为:随机选择一个变量 X i X_i Xi,然后根据其全条件概率 p ( x i ∣ x i ) p(x_i|\pmb{x}_{\\i}) p(xi∣xxxi)来设置其状态,即以 p ( x i = 1 ∣ x i ) p(x_i=1|\pmb{x}_{\\i}) p(xi=1∣xxxi)的概率将变量 X i X_i Xi设为1,否则设为0.在固定温度T的情况下,在运行足够时间之后,玻尔兹曼机会达到热平衡。此时,二和全局状态的概率服从玻尔兹曼机 p ( x ) p(\pmb{x}) p(xxx),只与系统的能量有关,与初始状态无关。
要使得玻尔兹曼机到达热平衡,其收敛速度和温度T相关。
当系统温度非常高 T → ∞ T \to \infty T→∞时, p ( x i = 1 ∣ x i ) → 0.5 p(x_i=1|\pmb{x}_{\\i}) \to 0.5 p(xi=1∣xxxi)→0.5,即每个变量状态的改变十分容易,每一种系统状态都是一样的,从而很快可达到热平衡。
当系统温度非常低 T → 0 T \to 0 T→0,如果 Δ E i ( x i ) > 0 \Delta E_i(\pmb{x}_{\\i})>0 ΔEi(xxxi)>0,则 p ( x i = 1 ∣ x i ) → 1 p(x_i=1|\pmb{x}_{\\i}) \to 1 p(xi=1∣xxxi)→1;如果 Δ E i ( x i ) < 0 \Delta E_i(\pmb{x}_{\\i})<0 ΔEi(xxxi)<0,则 p ( x i = 1 ∣ x i ) → 0 p(x_i=1|\pmb{x}_{\\i}) \to 0 p(xi=1∣xxxi)→0,即:
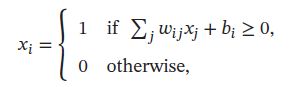
因此,当 T → 0 T\to0 T→0时,随机性方法变成了确定性方法,这时,玻尔兹曼机退化成一个Hopfield网络。
Hopfield网络是一确定性的动力系统,而玻尔兹曼机是一种随机性的动力系统,Hopfield网络的每次状态更新都会使得系统的能量降低,而玻尔兹曼机则以一定概率事系统能量上升,下图是Hopfield网络和玻尔兹曼机运行时系统能量变化对比:
1.2 能量最小化与模拟退火
在一个动力系统中,找到一个状态使系统能量最小是一个十分重要的优化问题。如动力系统是确定性的,如Hopfield网络,一个简单(但低效)的能量最小化是随机选择一个变量,其他变量保持不变,将这个能量设为使网络能量更低的状态。当每个变量 X i X_i Xi取值为 0 , 1 {0,1} 0,1时,如果能量差异 Δ E i ( x i ) > 0 \Delta E_i(\pmb{x}_{\\i})>0 ΔEi(xxxi)>0,则设 X i = 1 X_i=1 Xi=1,否则 X i = 0 X_i=0 Xi=0。
这种方法的解是局部最优的,为跳出局部最优,必须允许偶尔可以将一个变量设为使得能量变高的状态。故引入一定的随机性,以 σ ( Δ E i ( x i ) T ) \sigma(\frac{\Delta E_i (\pmb{x}_{\\i})}{T}) σ(TΔEi(xxxi))的概率将变量 X i = 1 X_i=1 Xi=1,否则 X i = 0 X_i=0 Xi=0。类似吉布斯采样过程。
要使动力系统达到热平衡,温度T选择十分关键,一个这种方法是让系统刚开始在一个比较高的温度下运行达到热平衡,然后逐渐降低,直到系统在一个比较低的温度下运行到达热平衡。这样就可以得到一个能量最小的分布。这个过程是模拟退火(Simulated Annealing)。
模拟退火是一种寻找全局最优的近似方法,名字来源于冶金学“退火”,即将材料加热后再以一定的速度退火冷却,减少晶格中的缺陷。可证明模拟退火算法所得到解依概率收敛到全局最优解。
1.3 参数学习
不失一般性,假设一个玻尔兹曼机有K个变量,包括 K v K_v Kv个可观测变量 v ∈ { 0 , 1 } K v \pmb{v}\in\{0,1\}^{K_v} vvv∈{ 0,1}Kv和 K h K_h Kh个隐变量 h ∈ { 0 , 1 } K h \pmb{h}\in\{0,1\}^{K_h} hhh∈{ 0,1}Kh。
给定一组可观测的向量 D ∈ { v ^ ( 1 ) , v ^ ( 2 ) , ⋯ , v ^ ( N ) } D\in\{\hat{\pmb{v}}^{(1)},\hat{\pmb{v}}^{(2)},\cdots,\hat{\pmb{v}}^{(N)}\} D∈{ vvv^(1),vvv^(2),⋯,vvv^(N)}作为训练集,要学习玻尔兹曼机的参数 W \pmb{W} WWW和 b \pmb{b} bbb使得训练集中所有样本的对数似然函数最大,训练集的对数似然函数定义为:

对数似然函数对参数 θ \theta θ的偏导数为:
其中 p ^ ( v ) \hat{p}(\pmb{v}) p^(vvv) 表示可观测向量在训练集上的实际经验分布, p ( h ∣ v ) p(\pmb{h}|\pmb{v}) p(hhh∣vvv)和 p ( v , h ) p(\pmb{v},\pmb{h}) p(vvv,hhh)为在当前参数 W \pmb{W} WWW, b \pmb{b} bbb条件下玻尔兹曼机的条件概率和联合概率。
根据公式:
E ( v , h ) = E ( x ) = − ( ∑ i < j w i j x i x j + ∑ i b i x i ) E(\pmb{v},\pmb{h})=E(\pmb{x})=-(\sum_{i
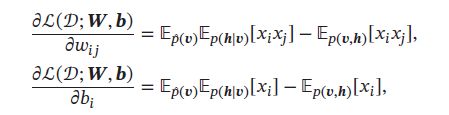
其中 i , j ∈ [ 1 , K ] i,j\in[1,K] i,j∈[1,K]。这两个公式涉及计算配分函数和期望,难精确。当K比较大时,配分函数和期望计算耗时,故玻尔兹曼机常用MCMC方法(如吉布斯采样)来近似求解。
以参数 w i j w_{ij} wij的梯度为例,公式:

中第一项在限定可观测变量 v \pmb{v} vvv为训练样本的条件下 x i x j x_ix_j xixj的期望。为了近似这个期望,可固定可观测变量 v \pmb{v} vvv,只对 h \pmb{h} hhh进行吉布斯采样。当玻尔兹曼机达到热平衡状态时,采样 x i x j x_ix_j xixj的值,在训练集上所有的训练样本重复此过程,得到 x i x j x_ix_j xixj的近似期望 ( x i x j ) d a t a (x_ix_j)_{data} (xixj)data。
以参数 b i b_{i} bi的梯度为例,公式:
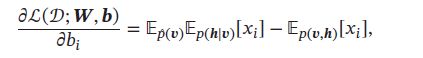
中第二项为玻尔兹曼机在没有任何限制条件下 x i x j x_ix_j xixj的期望。这时可以对所有变量进行吉布斯采样,当玻尔兹曼机达到热平衡时,采样 x i x j x_ix_j xixj的值,得到近似期望 ( x i x j ) m o d e l (x_ix_j)_{model} (xixj)model.
当采用梯度上升法,权重 w i j w_{ij} wij可用下面公式近似地更新:
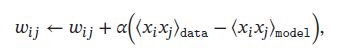
其中 α > 0 \alpha>0 α>0 为学习率,此更新方法一特点是仅仅使用了局部信息。即虽然优化目标是整个网络的能量最低,但每个权重的更新只依赖于它连接的相关变量的状态,这种学习方式和人脑神经网络的学习方式赫布规则(Hebbian Rule)十分类似
玻尔兹曼机可用于监督学习和无监督学习。监督学习中,可观测变量 v \pmb{v} vvv又可进一步分为输入和输出变量,隐变量则隐式地描述了输入和输出变量之间复杂的约束关系。无监督学习中,隐变量可看做可观测变量的内部特征表示。玻尔兹曼机也可以看做一种随机性的神经网络,是Hopfield神经网络的拓展,并且可以生成对应的Hopfield网络。没有时间限制时,玻尔兹曼机还可以用来解决复杂的组合优化问题。
2. 受限玻尔兹曼机
全连接的玻尔兹曼机太复杂,难广泛应用,虽然基于采样的方法很大程度上提高了学习效率,但每更新一次权重,就需要网络重新达到热平衡状态,过程低效。实际中,广泛应用的是一种带限制的版本,就是受限玻尔兹曼机。
受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)是一个二分图结构的无向图模型。受限玻尔兹曼机中的变量也分为隐变量和可观测变量。用可观测层和隐藏层来表示这两组变量,同一层中的节点之间没有连接,而不同层一个层中的节点与另一层中的所有节点连接,这和两层的全连接神经网络相同:

一个受限玻尔兹曼机由 K p K_p Kp个可观测变量和 K h K_h Kh个隐变量组成,定义如下:
- 可观测的随机向量 v ∈ R K v \pmb{v} \in \R^{K_v} vvv∈RKv
- 隐藏的随机向量 h ∈ R K h \pmb{h} \in \R^{K_h} hhh∈RKh
- 权重矩阵 W ∈ R K v × K h \pmb{W}\in \R^{K_v \times K_h} WWW∈RKv×Kh,其中每个元素 w i j w_{ij} wij为可观测变量 v i v_i vi和隐变量 h j h_j hj之间边的权重
- 偏置 a ∈ R K v \pmb{a} \in \R^{K_v} aaa∈RKv和 b ∈ R K h \pmb{b} \in \R^{K_h} bbb∈RKh,其中 a i a_i ai为每个可观测的变量 v i v_i vi的偏置, b i b_i bi为每个可观测的变量 h j h_j hj的偏置
受限玻尔兹曼机的联合概率分布 p ( v , h ) p(\pmb{v},\pmb{h}) p(vvv,hhh)定义为:
![]()
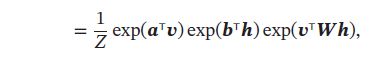
其中 Z = ∑ v , h e x p ( − E ( v , h ) ) Z = \sum_{v,h}exp(-E(\pmb{v},\pmb{h})) Z=∑v,hexp(−E(vvv,hhh))为分配函数
2.1 生成模型
在给定受限玻尔兹曼机的联合概率分布 p ( h , v ) p(\pmb{h},\pmb{v}) p(hhh,vvv)后,可以通过吉布斯采样方法生成一组服从 p ( h , v ) p(\pmb{h},\pmb{v}) p(hhh,vvv)分布的样本
全条件概率 吉布斯采样需要计算每个变量 V i V_i Vi和 H j H_j Hj的全条件概率。受限玻尔兹曼机中同层变量之间无连接,从无向图性质可知,给定可观测变量时,隐变量之间相互条件独立。同样,给定隐变量,可观测变量之间也相互条件独立,因此有:

其中 v i \pmb{v}_{\\i} vvvi为除变量 V i V_i Vi外其他可观测变量的取值, h i \pmb{h}_{\\i} hhhi为除变量 H i H_i Hi外其他隐变量的取值。因此, V i V_i Vi的全条件概率只需计算 p ( v i ∣ h ) p(v_i|\pmb{h}) p(vi∣hhh), H j H_j Hj的全条件概率只需计算 p ( h j ∣ v ) p(h_j|\pmb{v}) p(hj∣vvv)

受限玻尔兹曼机的全条件概率中,可观测变量之间相互条件独立,隐变量之间也相互条件独立。因此,首先玻尔兹曼机可以并行地对所有的可观测变量(或隐变量)同时进行采样,从而更快到达热平衡。
吉布斯采样 受限玻尔兹曼机的采样过程如下:
- 给定或随机初始化一个可观测的向量 v 0 \pmb{v}_0 vvv0,计算隐变量的概率,并从中采样一个隐变量 h 0 \pmb{h}_0 hhh0
- 基于隐变量 h 0 \pmb{h}_0 hhh0,计算可观测变量的概率,并从中采样一个可观测的向量 v 1 \pmb{v}_1 vvv1
- 重复 t 次后,获得 ( v t , h t ) (\pmb{v}_t,\pmb{h}_t) (vvvt,hhht)
- 当 t → ∞ t \to \infty t→∞, ( v t , h t ) (\pmb{v}_t,\pmb{h}_t) (vvvt,hhht)的采样服从 p ( v , h ) p(\pmb{v},\pmb{h}) p(vvv,hhh)分布
2.2 参数学习
和玻尔兹曼机一样,受限玻尔兹曼机通过最大化似然函数来找到最优的参数 W , a , b \pmb{W},\pmb{a},\pmb{b} WWW,aaa,bbb。给定一组训练样本 D = { v ^ ( 1 ) , ⋯ , v ^ ( N ) } D=\{\hat{\pmb{v}}^{(1)}, \cdots, \hat{\pmb{v}}^{(N)}\} D={ vvv^(1),⋯,vvv^(N)},其对数似然函数为:
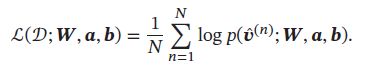
和玻尔兹曼机类似,受限玻尔兹曼机的对数似然函数 L ( D ; W , b ) L(D;\pmb{W},\pmb{b}) L(D;WWW,bbb)对参数的偏导数为:
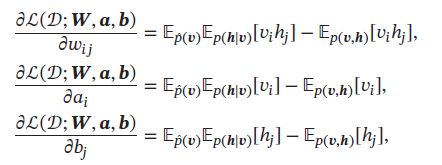
其中 p ^ ( v ) \hat{p}(\pmb{v}) p^(vvv)为训练数据集上 v \pmb{v} vvv的实际分布。
上述公式,都需要计算配分函数Z以及两个期望 E p ( h ∣ v ) E_{p(h|v)} Ep(h∣v)和 E p ( h , v ) E_{p(h,v)} Ep(h,v),因此很难计算,故用MCMC方法近似。
首先,将可观测向量 v \pmb{v} vvv设为训练样本中的值并固定,然后根据条件概率对隐向量 h \pmb{h} hhh进行采样,受限玻尔兹曼机的值记为 ( ⋅ ) d a t a (\cdot)_{data} (⋅)data。然后再不固定可观测向量 v \pmb{v} vvv,通过吉布斯采样来轮流更新 v \pmb{v} vvv和 h \pmb{h} hhh,当达到热平衡状态时,采集 v \pmb{v} vvv和 h \pmb{h} hhh的值,记为 ( ⋅ ) m o d e l (\cdot)_{model} (⋅)model
采用梯度上升方法,参数 W , a , b \pmb{W},\pmb{a},\pmb{b} WWW,aaa,bbb可利用下面公式近似更新:

其中 α > 0 \alpha > 0 α>0为学习率
根据受限玻尔兹曼机的条件独立性,可以对可观测变量和隐变量进行分组轮流采样,这样受限玻尔兹曼机的采样效率会有很大提高,但仍需经过很多步采样才可以采集到的符合真实分布的样本。
2.2.1 对比散度学习算法
由于受限玻尔兹曼机的特殊结构,因此可以使用一种吉布斯采样更有效的学习算法,即对比散度(Contrastive Divergence)。对比散度算法仅需k步吉布斯采样。
为提高效率,对比散度算法用一个训练样本作为可观测向量的初始值,然后交替对可观测向量和隐向量进行吉布斯采样,不需等到收敛,只需k步就足够。这就是CD-k算法,通常k=1就可以学得很好。对比散度的流程:

2.3 受限玻尔兹曼机的类型
实际中,处理的数据不一定是二值的,也可能是连续值,为能够处理这些数据,就需要根据输入或输出的数据类型来设计新的能量函数。
常见的受限玻尔兹曼机有三种:
-
“伯努利-伯努利”受限玻尔兹曼机(Bernoulli-Bernoulli RBM, BB-RBM):上面介绍的可观测变量和隐变量都为二值类型的受限玻尔兹曼机
-
“高斯-伯努利”尔兹曼机(Bernoulli-Bernoulli RBM, BB-RBM):可观测变量为高斯分布,隐变量为伯努利分布,其能量函数定义为:
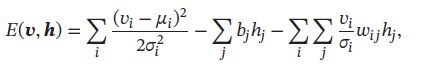
其中每个可观测变量 v i v_i vi服从 ( μ i , σ i ) (\mu_i,\sigma_i) (μi,σi)的高斯分布 -
“伯努利-高斯”受限玻尔兹曼机(Bernoulli-Gaussian RBM, BG-RBM):可观测变量为伯努利分布,隐变量为高斯分布,其能量函数定义为

其中每个隐变量 h j h_j hj服从 ( μ i , σ i ) (\mu_i,\sigma_i) (μi,σi)的高斯分布。
3. 深度信念网络
深度信念网络(Deep Belief Network,DBN)是一种深层的概率有向图模型,其图结构由多层的节点构成。每层节点的内部没有连接,相邻两层节点之间为全连接。网络的最底层为可观测变量,其它层节点为隐变量。最顶层的两层间的连接时无向的,其它层之间的连接时有向的:
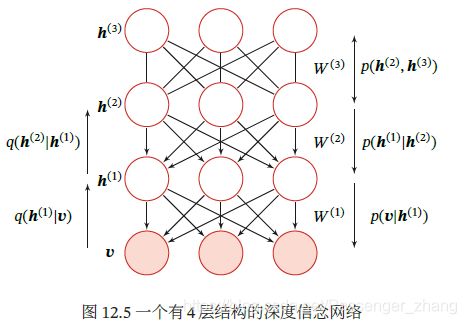
对一个有L层隐变量的深度信念网络,令 v = h ( 0 ) \pmb{v}=\pmb{h}^{(0)} vvv=hhh(0)表示最底层(0)为可观测变量, h ( 1 ) , ⋯ , h ( L ) \pmb{h}^{(1)},\cdots, \pmb{h}^{(L)} hhh(1),⋯,hhh(L)表示其余每层的变量,顶部的两层是一个无向图,可以看做是一个受限玻尔兹曼机,用来产生 p ( h ( L − 1 ) ) p(\pmb{h}^{(L-1)}) p(hhh(L−1))的先验分布。除了最顶上两层外,每一层变量 h ( l ) \pmb{h}^{(l)} hhh(l)依赖于其上一层 h ( l + 1 ) \pmb{h}^{(l+1)} hhh(l+1),即:
![]()
其中 l = { 0 , ⋯ , L − 2 } l=\{0,\cdots,L-2\} l={ 0,⋯,L−2}
深度信念网络中所有变量的联合概率可以分解为:

其中 p ( h ( l ) ∣ h ( l + 1 ) ) p(\pmb{h}^{(l)}|\pmb{h}^{(l+1)}) p(hhh(l)∣hhh(l+1))为Sigmoid型条件概率分布:
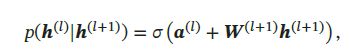
其中 σ ( ⋅ ) \sigma(\cdot) σ(⋅)为按位计算的logistic sigmoid函数, a ( l ) \pmb{a}^{(l)} aaa(l)为偏置参数, W ( l + 1 ) \pmb{W}^{(l+1)} WWW(l+1)为权重参数。每一个层可看做一个Sigmoid信念网络
3.1 生成模型
深度信念网络是一个生成模型,可用来生成符合特定分布的样本,隐变量用来描述在可观测变量之间的高阶相关性,加入训练数据服从分布 p ( v ) p(\pmb{v}) p(vvv),通过训练得到一个深度信念网络。
生成样本时,首先在最顶两层进行足够多的吉布斯采样,生成 h ( l + 1 ) \pmb{h}^{(l+1)} hhh(l+1),然后依次计算下一层隐变量的分布。因在给定上一层变量取值时,下一层的变量是条件独立的,故可独立采样。这样,从第 L − 1 L-1 L−1层开始,自顶向下进行逐层采样,最终得到可观测层的样本。
3.2 参数学习
深度信念网络最直接的训练方式是最大化可观测变量的边际分布 p ( v ) p(\pmb{v}) p(vvv)在训练集上的似然 。但是在深度信念网络中,隐变量 h \pmb{h} hhh之间的关系十分复杂,由于“贡献度分配问题”,很难直接学习。即使对于简单的单层Sigmoid信念网络:
![]()
在已知可观测变量时,其隐变量的联合后验概率 p ( h ∣ v ) p(\pmb{h}|v) p(hhh∣v)不再相互独立,因此很难估计所有隐变量的后验概率,早期深度信念网络的后验概率一般通过蒙特卡洛方法或变分方法来近似估计,但效率低,从而导致其参数学习比较困难。
为了有效训练深度信念网络,我们将每一层的Sigmoid信念网络转换为受限玻尔兹曼机,这样做的好处是隐变量的后验概率事相互独立的,从而可容易进行采样。这样,深度信念网络可看做多个受限玻尔兹曼机从下到上进行堆叠,第 l l l层受限玻尔兹曼机的隐层作为第 l + 1 l+1 l+1受限玻尔兹曼机的可观测层。进一步,深度信念网络课采用逐层训练的方式来快速训练,即从最底层开始,每次只训练一层,直到最后一层。
深度信念网络的训练过程可分为逐层预训练和精调两个阶段,先通过逐层预训练将模型的参数初始化为较优的值,然后通过传统机器学习方法对参数进行精调。
3.2.1 逐层预训练
采用逐层训练的方式,将深度信念网络的训练简化为对多个受限玻尔兹曼机的训练。
具体的逐层训练过程为自下而上依次训练每一层的首先玻尔兹曼机。假设已训练好前 l − 1 l-1 l−1层的受限玻尔兹曼机,可计算隐变量自下而上的条件概率:

这样可按照 v = h ( 0 ) → ⋯ → h ( l − 1 ) \pmb{v} = \pmb{h}^{(0)} \to \cdots \to\pmb{h}^{(l-1)} vvv=hhh(0)→⋯→hhh(l−1)的顺序生成一组 h ( l − 1 ) \pmb{h}^{(l-1)} hhh(l−1)的样本,记为 H ^ ( l − 1 ) = { h ^ ( l , 1 ) , ⋯ , h ^ ( l , M ) } \pmb{\hat{H}}^{(l-1)}=\{\pmb{\hat{h}}^{(l,1)},\cdots,\pmb{\hat{h}}^{(l,M)} \} H^H^H^(l−1)={ h^h^h^(l,1),⋯,h^h^h^(l,M)}。然后将 h ( l − 1 ) \pmb{h}^{(l-1)} hhh(l−1)和 h ( l ) \pmb{h}^{(l)} hhh(l)组成一个受限玻尔兹曼机,用 H ^ ( l − 1 ) \pmb{\hat{H}}^{(l-1)} H^H^H^(l−1)作为训练集充分训练第 l l l 层的受限玻尔兹曼机

大量时间表明,逐层预训练可以产生非常好的参数初始值,从而极大地降低了模型的学习难度。

3.2.1 精调
经过预训练,再结合具体的任务(监督或无监督学习),通过传统的全局学习算法对网络进行精调(fine-tuning),使模型收敛到更好的局部最优点。
作为生成模型的精调 除了顶层的受限玻尔兹曼机,其它层之间的权重可以被分为向上的认知权重(Recognition Weight) W ′ \pmb{W}^{'} WWW′和向下的生成权重(Generative Weight) W \pmb{W} WWW。认知权重用来计算后验概率,生成权重用来定义模型,认知权重初始值 W ′ ( l ) = W ( l ) T \pmb{W}^{'^{(l)}}=\pmb{W}^{ {(l)}^T} WWW′(l)=WWW(l)T
深度信念网络一般采用 Contrastive Wake-Sleep算法进行精调:
- Wake阶段:认知过程,通过外界输入(可观测变量)和向上的认知权重,计算每一层隐变量的后验概率并采样。修改下行的生成权重使得下一层的变量的后验概率最大。
- Sleep阶段:生成过程,通过顶层的采样和向下的生成权重,逐层计算每一层的后验概率并采样。然后,修改向上的认知权重使得上一层变量的后验概率最大。
- 交替进行Wake和Sleep过程,直到收敛
作为判别模型的精调 深度信念网络的一个应用是作为深度神经网络的预训练模型,提供神经网络的初始权重,这时只需要向上的认知权重,作为判别模型使用:
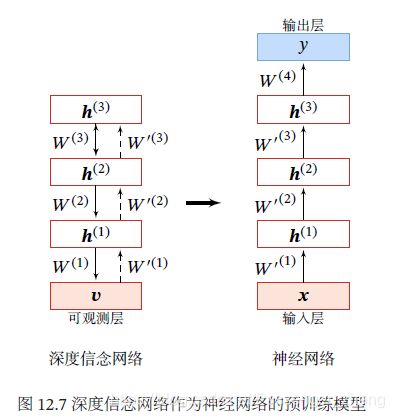
具体的精调过程为:在深度信念网络的最顶层增加一层输出层,然后使用反向传播算法对这些权重进行调优。在训练数据少时,预训练的作用非常大,因不恰当的初始化权重会显著影响最终模型的性能,而预训练获得的权重在权重空间中比随机权重更接近最优的权重,避免了反向传播算法因随机初始化权值参数而容易陷入局部最优和训练时间长的缺点。