【神经网络的训练技巧】Bag of Tricks for Image Classification with Convolutional Neural Networks

【神经网络的训练tricks】Bag of Tricks for Image Classification with Convolutional Neural Networks

用卷积神经网络进行图像分类的锦囊妙计

0.Abstract

​ 最近在图像分类研究中取得的大部分进展都可以归功于训练程序的改进，例如数据增强和优化方法的改变。然而，在文献中，大多数的改进要么作为实现细节被简要提及，要么只在源代码中可见。在本文中，我们将对这类改进的方法进行研究，并通过消融实验(控制变量法)实证评估其对最终模型精度的影响。结果表明，通过将这些改进结合在一起，我们将能够显著改善各种CNN模型。例如，我们提高ResNet-50的top-1验证精度,在ImageNet上从75.3%提高到79.29%。我们还将证明图像分类精度的改善会导致其他应用领域（如目标检测和语义分割)有更好的迁移学习性能。

1.Introduction

​ 自2012年AlexNet问世以来，深度卷积神经网络已经成为图像分类的主流方法。此后，各种新的架构被提出，包括VGG、NiN、Inception、ResNet、DenseNet和NASNet。同时，我们也看到了模型精度稳步提高的趋势。例如，ImageNet上的Top-1验证精度已经从62.5%（AlexNet）提升到82.7%（NASNet-A）。然而，这些进步并不仅仅来自于模型结构的改进。训练过程的改进，包括损失函数、数据预处理和优化方法的改变也发挥了重要作用。在过去的几年里，人们提出了大量这样的改进措施，但受到的关注相对较少。在文献中，大多数（训练技巧）只是作为实现细节被简单提及，而其他的则只能在源代码中发现。

​ 在本文中，我们将研究一系列训练过程和模型架构的改进，这些改进可以提高模型的准确率，但几乎不改变计算复杂性。其中很多都是小 “技巧”，比如修改某个卷积层的步长大小，或者调整学习率策略（learning rate schedule）。总之，它们会带来很大的改变。我们将在多个网络结构和数据集上评估它们，并报告它们对最终模型精度的影响。

​ 我们的实证评估表明，几种技巧都能带来显著的精度提升，将它们结合在一起可以进一步提升模型精度。我们将应用所有技巧后的ResNet-50与其他相关网络进行比较，见表1。请注意，这些技巧将ResNet50在ImageNet上的Top-1验证精度从75.3%提高到79.29%。它的表现也优于其他较新和改进的网络架构，如SE-ResNeXt-50。此外，我们还表明，我们的方法可以推广到其他网络（Inception V3和MobileNet）和数据集（Place365）。我们进一步表明，用我们的技巧训练的模型在其他应用领域带来了更好的迁移学习性能，如对象检测和语义分割。

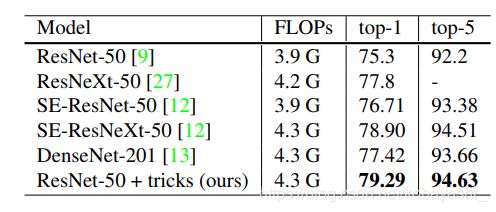
表1：不同模型的计算量和验证集精度。用我们的 "技巧 "训练出来的ResNet，能够胜过用标准pipeline训练出来的更新和改进的架构。

论文提纲：我们首先在第2节中建立了一个baseline训练流程，然后在第3节中讨论了几个在新的硬件上进行高效训练有用的技巧。在第4节中，我们回顾了ResNet的三个小的模型结构的调整，并提出了一个新改进方法。然后在第5节中讨论了四个额外的训练流程的改进。最后，我们在第6节研究这些更精确的模型是否可以帮助迁移学习。

​ 我们的模型实现和训练脚本在GluonCV中公开。

2.Training Precedures

​ 小批量随机梯度下降训练神经网络的模板如Algorithm 1所示。在每次迭代中，我们随机抽取b张图片计算梯度，然后更新网络参数，在K次通过数据集后停止。Algorithm 1中的所有函数和超参数都可以用许多不同的方式实现。在本节中，我们首先指定算法1的baseline实现。

初始化网络；

当没有到达设定的轮数：

​ 当没有遍历整个数据集：

​ 随机采样bath_size个图片；

​ 图片数据预处理；

​ 前向；

​ 计算loss；

​ 梯度反传；

​ 权重更新；

2.1 Baseline Training Procedure

我们使用一个广泛运用的ResNet的实现作为我们的baseline。训练和验证之间的预处理pipeline是不同的。在训练过程中，我们会逐一执行以下步骤:

1.随机采样一张图片，并将它编码为32-bit浮点，值域在[0,255]。

2.随机裁剪一个长宽比在[3/4.4/3]，面积占比在[8%，100%]的正方形区域，然后将该区域调整为$224\times 224$的方形图片。

3.50%概率水平翻转。

4.缩放色调、饱和度和亮度，系数统一取自[0.6，1.4]。

5.加入PCA噪声，其系数从正态分布N（0，0.1）中采样。

6.归一化RGB通道，分别先减去123.68，116.779，103.939，然后除以58.393，57.12，57.375。

​ 在验证过程中，我们先将每张图像的短边调整为256像素，同时保持其长宽比。接下来，我们裁剪出中心的$224\times 224$区域，并对RGB通道进行类似训练时候的归一化。在验证过程中，我们不进行任何随机增强。

​ 卷积层和全连接层的权重都使用Xavier¹初始化。 我们将参数的值从$[-a,a]$，其中$a=\sqrt{6/(d_{in}+d_{out})}$。这里，$d_{in},d_{out}$为输入和输出通道的大小，所有的bias设为0.对于BN层，$\gamma$初始化为1，$\beta$设置为0.

​ 训练用Nesterov加速梯度（NAG）下降。每个模型在8个Nvidia V100 GPU上训练120个epoch，总批次大小为256。学习率初始化为0.1，并在第30、60和90个epoch时除以10。

2.2 Experiment Results

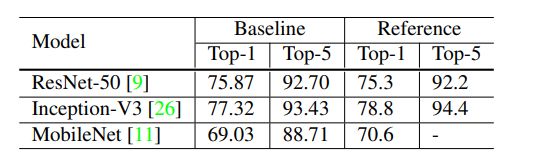
​ 我们评估了3种CNN：ResNet-50，Inception-V3和MobileNet。对于Inception-V3,我们将输入调整为了299*299。我们使用ISLVRC2012数据集，它包含有1000类的1.3百万张图片。测试精度如表2所示。可以看到，我们的ResNet-50结果比参考的结果稍微好一些，而我们的MobileNet由于不同的训练过程，精度比参考结果稍微低一些。

3.Efficient Training

​ 近年来，硬件，尤其是GPU发展迅速。因此，许多与性能相关的折衷的最佳选择已经发生了变化。例如，现在在训练过程中使用较低的数值精度和较大的批处理量更为有效。在本节中，我们回顾了各种技术，这些技术可以在不牺牲模型精度的情况下实现低精度和大批量训练。有些技术甚至可以同时提高准确性和训练速度。

3.1 Large-batch training

​ Mini-batch SGD将多个样本分组到一个minibatch中，以提高并行性，降低通信成本。然而，使用大批量尺寸可能会减慢训练进度。对于凸问题，收敛速度随着批处理量的增加而降低。对于神经网络也有类似的实验结果的证明。换句话说，在相同的Epoch下，与使用较小批量规模训练的模型相比，使用大批量规模的训练会导致模型的验证精度下降。（因为收敛也慢了）

​ 多个文章提出了解决这个问题的启发式方法。在下面的段落中，我们将研究四种有助于扩大单机训练（single machine training）批次规模的启发式方法。

Linear scaling learning rate(线性缩放学习率) 在mini-batch SGD中，梯度下降是一个随机过程，因为每个批次的样本都是随机选择的。增加批次大小不会改变随机梯度的期望值，但会降低其方差。换句话说，大的批次大小可以减少梯度中的噪声，所以我们可以提高学习率，使得梯度下降地更大（make a larger progress along the opposite of the gradient direction ）。Goyal等人证明，随着批次大小线性增加学习率，对于ResNet-50训练来说，经验上是可行的。具体来说，如果我们按照He等人[9]选择0.1作为批量大小256的初始学习率，那么当换成更大的批量大小$b$时，我们将把初始学习率提高到$0.1\times b/256$。

Learning rate warmup 在训练的初期，所有的参数都是随机初始化的，因此离最终解很远。使用一个大的学习率可能会导致数值的不稳定。在warmup启发式方法中，我们在开始时使用一个小的学习率，当训练过程稳定后再切换回初始学习率。Goyal等人提出了一种渐进式warmup策略，将学习率从0线性增加到初始学习率。换句话说，假设我们将使用前$m$个批次（如5个数据epoch）进行热身，初始学习率为$\eta$，那么在第$i$个批次，$1\le i\le m$时，我们将学习率设置为$i\eta /m$。

Zero $\gamma$ 一个ResNet网络由多个残差块组成，每个残差块由多个卷积层组成。给定输入$x$，假设$block(x)$是块中最后一层的输出，那么这个残差块输$x+block(x)$。需要注意的是，块的最后一层可以是一个批归一化（BN）层。BN层首先对其输入进行标准化，用$xˆ$表示，然后进行尺度变换$\gamma xˆ+\beta$。$\gamma$和$\beta$都是可学习的参数，分别初始化为$\gamma =1$和$\beta =0$。在零$\gamma$初始化启发式中，我们对所有位于残差块末端的BN层初始化$\gamma =0$。因此，所有残差块只是返回它们的输入，模仿层数较少的网络，在初始阶段更容易训练。

No bias decay 权重衰减通常应用于所有可学习参数，包括权重和偏置。这相当于对所有参数应用L2正则化，使其值趋向于0.但正如Jia等人所指出的，建议只对权重应用正则化，以避免过拟合。无偏置衰减启发式方法遵循这一建议，它只对卷积层和全连接层中的权重应用权重衰减。其他参数，包括BN层中的偏置和γ和β，都不进行正则化。

​ 需要注意的是，LARS提供了层间自适应学习率，并且据报道对极大的批处理量（超过16K）是有效的。而在本文中，我们只限于对单机训练的方法，在这种情况下，不超过2K的批次大小往往能带来良好的系统效率。

3.2 Low -precision training

​ 神经网络通常在32位浮点（FP32，单精度）精度下训练，也就是说，所有地数值都是以FP32格式存储的，算术运算的输入和输出也都是FP32的。不过，新的硬件可能会有针对较低精度数据类型的增强算术逻辑单元。例如，前面提到的Nvidia V100在FP32下，有14 TFLOPS，但在FP16，了超过100 TFLOPS。如表3，在V100上从FP32切换到FP16后，整体训练速度加快了2到3倍。

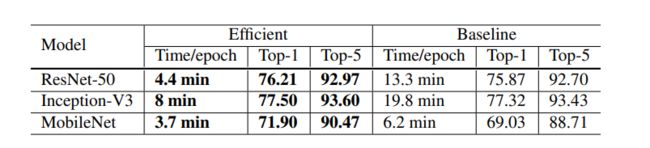
表3：ResNet-50的训练时间和验证精度在baseline（BS=256和FP32）和Efficient的方法（BS=1024和FP16）之间的比较

​ 尽管性能上有优势，但精度降低后的数值表示范围更窄，使得结果更容易偏离范围，然后对训练产生影响。Micikevicius等提出将所有参数和激活存储在FP16中，并使用FP16来计算梯度。同时，所有参数在FP32中都有一个副本，用于参数更新。此外，为了更好地将梯度的范围调整到FP16中，对loss乘以一个标量也是一种实用的解决方案。

3.3 Experiment Results

​ ResNet-50的评价结果见表3。与批次大小256和FP32的baseline相比，使用较大1024批次大小和FP16将ResNet-50的训练时间从每epoch13.3分钟缩短到每epoch4.4 min。此外，通过对大批量训练的所有启发式算法进行叠加，与基线模型相比，1024批大小和FP16训练的模型甚至略微提高了0.5%的top-1精度。

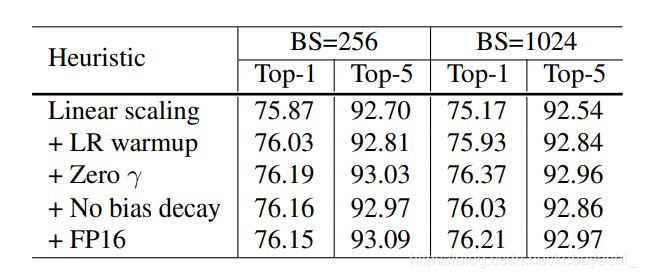
​ 所有启发式方法的消融研究如表4所示。单纯通过线性缩放学习率将批处理量从256增加到1024，导致top-1的准确率下降了0.9%，而堆叠其余三种启发式可以弥补这一差距（bridges the gap）。训练结束时从FP32切换到FP16并不影响准确率。

表4：各有效训练启发式方法对ResNet-50的效果。

4.Model Tweaks(模型调整)

pass

5.Training Refinements

​ 在这一部分，我们将描述4个训练增强的方法来进一步提高模型精度。

5.1 Cosine Learning Rate Decay

​ 学习率的调整对训练至关重要。在使用3.1节描述的学习率warmup之后，我们通常会从初始学习率稳步降低数值。被广泛使用的策略是对学习率进行指数化的衰减。He等每30个epoch以0.1的加权降低学习率，我们称之为 “阶梯式衰减”。Szegedy等人每两个epoch以0.94的加权递减学习率。

​ 与之相反，Loshchilov等人提出了余弦退火策略（consine annealing strategy）。一个简化的版本是通过遵循余弦函数将学习率从初始值降到0。假设批次总数为$T$（忽略warmup阶段），那么在批次$t$，学习率${\eta }_t$的计算公式²为：
$${\eta }_t=\frac{1}{2}(1+cos(\frac{t\pi }{T}))\eta$$
其中，$\eta$是初始学习率，我们称这种方法为余弦衰减。

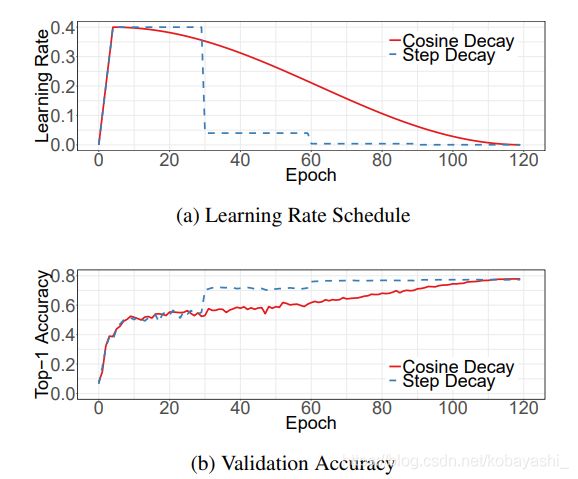
图3：可视化的使用warmup的learning rate schedule。a.批量大小1024的cosine和step schedule。b.关于两个schedule的top-1验证精度曲线。

从b可以知道，在训练的后期，lr越小，精度越高

图3a为阶跃衰减和余弦衰减的比较。可以看出，余弦衰减在开始的时候学习速度缓慢，到了中间就变得几乎是线性下降，到了最后又放慢了速度。与阶梯衰减相比，余弦衰减从一开始就开始衰减学习，但一直到阶梯衰减将学习率降低10倍时，余弦衰减的学习率仍然很大，有可能提高训练进度。

5.2 Label Smoothing

​ 图像分类网络的最后一层通常是大小等于标签数量的全连接层，用$k$表示，以输出预测的置信度得分。给定一幅图像，$z_i$表示第$i$类的预测得分，这些得分通过$softmax$算子进行归一化，转为预测概率。用$q$表示$softmax$算子的输出，$q=softmax(x)$，则第$i$类的概率$q_i$,可以通过以下方式计算：
$$q_i=\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}$$
显然，$q_i>0$且${\sum }_{i=1}^K{q}_i=1$,所以$q$是一个有效的概率分布。

​ 另一方面，假设这个图像的真实标签是$y$，我们可以构造一个真值概率分布为：如果$i=y$，则$p_i=1$，否则为0。在训练过程中，我们尽量最小化负交叉熵损失来更新模型参数，使得这两个概率分布彼此靠近。
$$l(p,q)=-\sum _{i=1}^K{q}_{i}log{p}_i$$
在$p$已知的情况下，$l(p,q)=-log{p}_y=-z_y+log({\sum }_{i=1}^K{e}^{z_i})$换句话说，最佳解是$z_y^{\ast }=inf$³,同时保持其他的足够小。换句话说，它鼓励输出得分显著不同，而这可能导致过拟合。

​ 标签平滑（label smoothin）的思想首先在Inception-v2中提出，它将真实概率的组成变为
KaTeX parse error: Unknown column alignment: 1 at position 30: …\begin{array} 1̲ 1-\epsilon\ \…
其中$ϵ$是一个小常量，现在最优解变为了
$$z_i^{\ast }=\{\begin{array}{l}log((K-1)(1-ϵ)/ϵ)ifi=y,\\ \alpha otherwise,\end{array}$$
$\alpha$是任意的实数。这样做会鼓励全连接层的输出是一个有限的值，从而获得更好的泛化性。

​ 当ε=0时，差距函数$log((K-1)(1-\epsilon )/\epsilon )$将为$\infty$，随着$\epsilon$的增大，差距（gap）减小。具体来说，当$\epsilon =(K-1)/K$时，所有最优的$z_i^{\ast }$将是相同的。图4a显示了随着我们移动$\epsilon$，给定K = 1000的ImageNet数据集的差距如何变化。

When$ ε = 0$, the gap $log((K − 1)(1 − ε)/ε) $willbe\infty andas\epsilon increases,thegapdecreases.Specificallywhen$ ε = (K − 1)/K$, all optimal $z ^∗_ i $will be identical. Figure 4a shows how the gap changes as we move ε, given K = 1000 for ImageNet dataset.

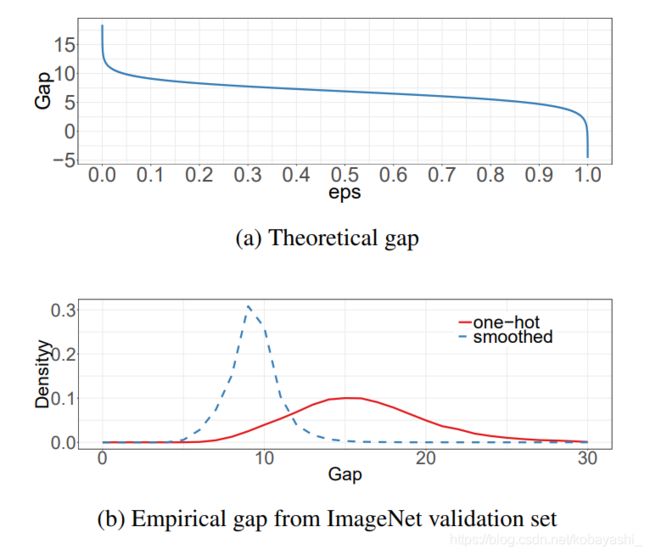
图4：可视化标签平滑技术在ImageNet上的有效性。上：$z_p^{\ast }$之间的理论差距。底：最大预测值和其余值的平均数之间的差距的经验分布。

​ 我们实证比较了两种输出值的ResNet-50-D模型，分别在有标签和无标签平滑的情况下进行训练，并分别计算最大预测值和其余的平均值之间的差距。在$\epsilon =0.1，K=1000$的情况下，理论差距约为 9.1。 图4b显示的两个模型在mageNet的验证集上进行预测差距分布情况。很明显，随着标签平滑化，分布中心趋于在理论值上且极端值较少。

5.3 Konwledge Distillation

​ 在知识蒸馏中，我们使用教师网络来帮助训练当前模型，一般称作学生网络。教师模型往往是预先训练好的模型，精度较高，通过模仿，学生模型能够在保持模型复杂度不变的情况下，提高自己的精度。一个例子是用ResNet-152作为教师模型来帮助训练ResNet-50。

​ 在训练的过程中，我们加入一个蒸馏损失来惩罚教师网络和学生网络之间的不同的softmax输出。给定一个输入，假设$p$是真实的概率分布，$z$和$r$分别是学生模型和教师模型最后一个全连接层的输出。记得之前我们用了一个负交叉熵损失$loss(p,softmax(z))$来衡量$p$和$z$之间的差异，这里我们再次在蒸馏上使用相同的损失。因此，损失改为
$$l(p,softmax(z))+T^{2}l(softmax(r/T),softmax(z/T))$$
其中，$T$是温度超参数，用于将softmax输出变得平滑，通过这样便可以从教师网络的预测中蒸馏知识⁴。

5.4 Mixup Training

​ 在2.1节中，我们介绍了如何在训练前对图像进行增强。在这里，我们考虑另一种叫做 mixup的增强方法。在 mixup 中，每次我们随机抽取两个样本$ (x_i , y_i) $和 $(x_j,y_j)$ 。然后我们通过对这两个例子进行加权线性插值形成一个新的样本：
$$\begin{gathered} \hat{x}=\lambda x_i+(1-\lambda )x_j \\ \hat{y}=\lambda y_i+(1-\lambda )y_i \end{gathered}$$
其中$\lambda \in [0，1]$是一个从$Beta(\alpha ，\alpha )$⁵分布中抽取的随机数。在混合训练中，我们只使用新的例子$（\hat{x}，\hat{y}）$。

5.4 Experiment Results

pass

总结：

---

1. http://machinelearning.wustl.edu/mlpapers/paper_files/AISTATS2010_GlorotB10.pdf ↩︎

2. 
   ,T=10，η=1，可见，t=10时,lr趋于0 ↩︎

3. $z_y^{\ast }=无穷$。一般$ϵ=0.1$标签平滑技术在知识蒸馏过程中一般不使用，硬标签会产生一个更好的教师网络。When does label smoothing help? ↩︎

4. KD也是一种标签平滑技术 ↩︎

5. 二项分布 ↩︎