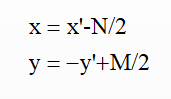Python+OpenCV图像处理（二）——几何变换

---

系列文章
Python+OpenCV图像处理（一）——OpenCV框架与图像插值算法
Python+OpenCV图像处理（二）——几何变换
Python+OpenCV图像处理（三）——彩色空间互换
Python+OpenCV图像处理（四）——图像滤波
Python+OpenCV图像处理（五）——图像阈值和二值化
Python+OpenCV图像处理（六）——边缘检测

---

二、几何变换

2.1 简介

几何变换，通常指的是对数字图像进行平移、旋转、镜像等。
通常在传统的cv领域，由于人为进行拍摄图像的时候，有很多干扰会导致拍摄角度有问题，需要对图像进行矫正处理，这个矫正的过程正是以几何变换为基础的。另外，在当下比较火热的深度学习领域，在有些情况下，由于样本数量较少，导致训练的模型不够理想，这时，需要自行得到较多的训练样本，这里就可以用到几何变换进行对图像数据进行扩增。
不同的几何变换，原理基本相似，只是变换矩阵有一定的差异。

2.2 算法理论

2.2.1 变换形式

从2.1可以知道，不同的变换形式只是变换矩阵有差异，这里先对这些差异进行研究。
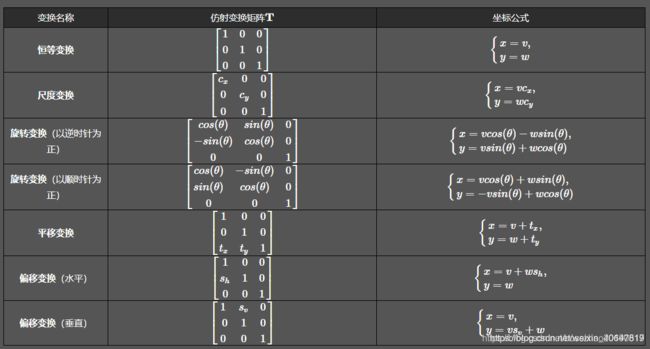
这里采用冈萨雷斯的《数字图像处理_第三版》的变换矩阵形式，与我们实现用到的OpenCV有些许差异，对于OpenCV我们可以参考它的官方文档。这里的仿射变换如下：

 

式中的T就是变换矩阵，其中 (v,w)为原坐标，(x,y) 为变换后的坐标，一些常见的变换矩阵及其对应的作用如下：

 

2.2.2 坐标系变换

我们知道，在平移和缩放的变换中，可以任意选择变换中心，然而对于旋转和偏移，则不能够随便选择了，我们一般情况下选择图像的中心点为变换中心。
然而图像坐标系和数学中的笛卡尔坐标系是不同的，在我们做几何变换的时候通常是以笛卡尔坐标系进行变换的。两种坐标系如下图：

 

具体变换是：

• 将输入原图图像坐标转换为笛卡尔坐标系；
• 进行旋转计算。旋转矩阵前面已经给出了；
• 将旋转后的图像的笛卡尔坐标转回图像坐标。

2.2.3 图像坐标系与笛卡尔坐标系转换关系

在图像中我们的坐标系通常是AB和AC方向的,原点为A，而笛卡尔直角坐标系是DE和DF方向的，原点为D，如图所示：

 

令图像表示为M×N的矩阵，对于点A而言，两坐标系中的坐标分别是(0，0)和(-N/2,M/2)，则图像某像素点(x’,y’)转换为笛卡尔坐标（x,y）转换关系为，x为列，y为行：

 

逆变换为：

 

于是，根据前面说的3个步骤（3次变换），旋转(顺时针旋转)的变换形式就为，3次变换就有3个矩阵：

 

根据上一节谈到的图像插值算法，我们这里用反向映射并通过插值得到输出图像对应未知的灰度值，即扫描输出图像的位置(x,y)，通过

 

（为T的逆矩阵）计算输入图像对应的位置 (v,w)。

2.3 OpenCV+Python实现

缩放

上节已经介绍了cv2.resize函数，这里不再详细展开。

平移

可以使用cv2.warpAffine实现几何变换，第一个参数为图片，第二个参数为变换矩阵，对于平移来说，就是平移的宽和高，第三个参数为输出图像的大小，注意行数等于高，列数等于宽。

#%%

import numpy as np
import cv2

img = cv2.imread('gogo.png',1)
#这里注意，由于图片为彩色，共三通道，所以对shape做切片操作
rows,cols = img.shape[:2]
print(rows,cols)
M = np.float32([[1,0,200],[0,1,100]])

dst = cv2.warpAffine(img,M,(cols,rows))

cv2.imshow('original img',img)
cv2.imshow('img',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

 

旋转

OpenCV提供了一个函数cv2.getRotationMatrix2D来构建旋转变换矩阵，第一参数为旋转中心；第二个参数为旋转角度，默认逆时针旋转；第三个参数为缩放比例。

#%%

import numpy as np
import cv2

img = cv2.imread('gogo.png',1)
rows,cols = img.shape[:2]

M1 = cv2.getRotationMatrix2D((cols/2.0,rows/2.0),45,0.7)
dst1 = cv2.warpAffine(img,M1,(cols,rows))

M2 = cv2.getRotationMatrix2D((cols/3.0,rows/2.0),90,0.5)
dst2 = cv2.warpAffine(img,M2,(cols,rows))

cv2.imshow('original img',img)
cv2.imshow('Rotate 45 degrees',dst1)
cv2.imshow('Rotate 90 degrees',dst2)
cv2.waitKey(0)
cv2.destroyAllWindows()

 

仿射变换

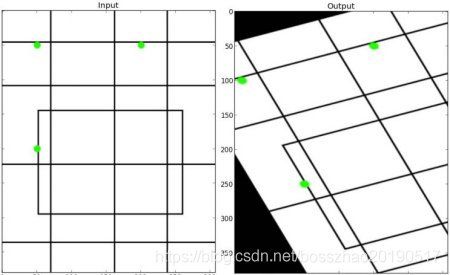
在仿射变换中，变换前后，平行之处仍然平行。为了找到变换矩阵，我们需要输入图像中的三个点及其在输出图像中的对应位置，利用cv2.getAffineTransform将创建一个2x3矩阵。图中绿点即为输入图像和输出图像对应的位置：

 

#%%

import numpy as np
import cv2
import matplotlib.pyplot as plt

img = cv2.imread('gogo.png',1)
rows,cols,channel = img.shape


pts1 = np.float32([[50,50],[400,50],[50,400]])
pts2 = np.float32([[100,200],[400,100],[40,450]])
M = cv2.getAffineTransform(pts1,pts2)
dst = cv2.warpAffine(img,M,(cols,rows))

plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()

cv2.imshow('original img',img)
cv2.imshow('affine transform',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

 

透视变换

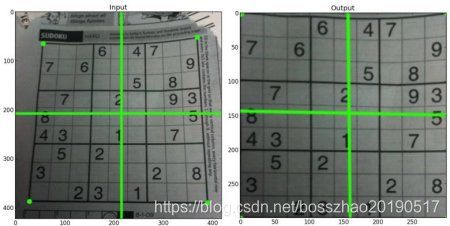
对于透视变换，需要3x3变换矩阵。转换前后，直线仍然保持直线。对于变换矩阵，需要找出输入和输出图像中对应的四个点，其中三个不能共线。通过函数cv.getPerspectiveTransform得到变换矩阵。然后用cv.warpPerspective将转换矩阵传入，原理如图：

 

#%%

import numpy as np
import cv2
import matplotlib.pyplot as plt

img = cv2.imread('gogo.png')
rows,cols,ch = img.shape
pts1 = np.float32([[200,65],[550,52],[200,600],[550,600]])
pts2 = np.float32([[0,0],[cols,0],[0,rows],[cols,rows]])
M = cv2.getPerspectiveTransform(pts1,pts2)
dst = cv2.warpPerspective(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()

cv2.imshow('original img',img)
cv2.imshow('affine transform',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()