机器学习评判指标

---

0.背景

机器学习通常评判一个算法的好坏，是基于不同场景下采用不同的指标的。通常来说，有：

• [x] 准确度；PR (Precision Recall)；
• [x] F测量；
• [ ] MCC；
• [ ] BM；
• [ ] MK；
• [ ] Gini系数；
• [x] ROC；
• [ ] Z score；
• [x] AUC ；
• [ ] Cost Curve；
• [ ] BLEU；
• [ ] Matthews correlation coefficient；
• [ ] METEOR；
• [ ] Brier score；
• [ ] NIST (metric)；
• [ ] ROUGE (metric)；
• [ ] Sørensen–Dice coefficient；
• [ ] Uncertainty coefficient, aka Proficiency；
• [ ] Word error rate (WER)；

从wiki获取一个很重要的二分类混淆矩阵来说明后续的内容。

图0.1 wiki上的图
图0.1为wiki上针对2分类的一个混淆矩阵，及对应的各种指标表示。其中：

• true condition：列表示真实类别；predicted condition：行表示预测的类别；
• 真实正类=true positive+false negative；真实负类=false positive+true negative；
• 预测的正类=true positive+false positive； 预测的负类=false negative+true negative。

1. 不同指标的含义

1.1 accuracy&Precision Recall

如图0.1所示:

• accuracy：（图0.1中ACC）即最常用的准确度，表示\(\frac{所有预测对了的样本个数}{总的样本个数}\)；
• Precision：（图0.1中PPV），精确率，表示预测的正类中预测对的样本个数比例\(\frac{true\, positive}{预测的正类}\)；
• Recall：（图0.1中TPR），召回率，表示真实正类中预测对的样本个数比例\(\frac{true\, positive}{真实正类}\).

1.2 F measure&&G measure

1.2.1 F measure

传统的F measure（balanced F score，\(F_1\) score）就是关于precision和recall的Harmonic均值（是数学上一种均值算法），其公式如下：

其中：

• 当F score为0的时候最差：即precision和recall中某个值或者都接近0，则该模型越差；
• 当F score为1的时候最好：即precision和recall同时越接近1则该模型越好。

ps：F1 score同样也被称为Sørensen–Dice coefficient或者说叫Dice similarity coefficient (DSC).

将上述式子表示成更通用的形式如下图：

其中 \(F_2\)， \(F_{0.5}\)是相对 \(F_1\)两个常用的F measure：

• 当\(\beta=2\)，则表示recall的影响要大于precision；
• 当\(\beta=0.5\)，则表示precision的影响要大于recall.

如果以图0.1中的type I error和type II error来表示F measure，则如下面式子：

1.2.2 G measure

相对于F measure 是一种Harmonic均值，G measure是一种geometric mean,同时也被称为 Fowlkes–Mallows index

即

1.3 PR Curve

针对2分类，以Recall为横轴，Precision为纵轴的曲线。如图2.1.1

1.4 Cost Curve

1.5 ROC

针对2分类，以图0.1中FPR为横轴，图0.1中TPR（也就是Recall）为纵轴的曲线。如图2.1.1

AUC：Aera under curve，即表示曲线下面积的意思

2. 不同指标之间的关系

早在1998年，Provost等人就认为简单的使用accuracy去评价算法的性能是完全不够的，因为会出现acc很高，而算法却相对是差的情况。所以他们推荐使用ROC来对算法进行评价。

2.1. PRC和ROC之间的关系

当不同类别中样本的个数差别很大的时候，ROC曲线是无法正确的描述算法性能的，假如2分类中负类特别多，那么当图0.1中FP变化很大时，在ROC上横坐标表示的FPR上表现的就不那么明显；而precision是通过FP与TP之间的对比而不是FP和TN之间的对比，从而如果FP变化很大的时候，precision就会变得很敏感了，从而能够抓取到当负类个数远大于正类时候算法性能的影响了。Jesse Davis以及前人就通过PRC来代替ROC进行算法性能描述。而这两种曲线之间一个很重要的区别就在于视觉上的体现，如图2.1.1所示。

图2.1.1 PR与ROC的曲线图
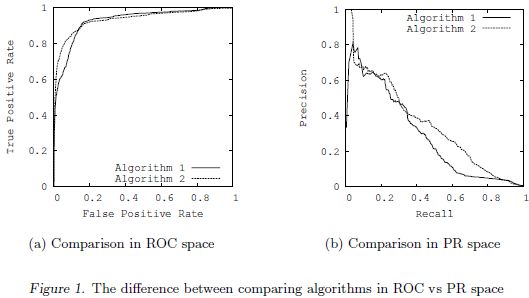
图2.1.1是基于同一个高度不平衡的数据集和同样的2个算法基础上，得到的ROC和PRC。ROC表示的算法当在拐角越接近左上角越好（即<左下-左上-右上>这样的顺序）；PRC表示的算法在拐角越接近右上角越好（即<左上-右上-右下>这样的顺序）。从中可以看出PRC更能给人以算法2要好于算法1的感觉。而ROC中虽然算法2的AUC更大，可是整体给人以这两种算法都很好了，只有细微差别的感觉。所以PRC不但可以放大2个算法之间的差别，还能看出这两种算法的发展空间还是很大的。

对于任何数据集来说（即有固定数据的正负类样本个数），基于同一个算法，PRC和ROC都包含了相同的点，也就是这两个曲线是具有等效性的，然而也保证了ROC中一个算法占优那么有且仅有该算法在PRC中也占优；可是如果一个算法在ROC中占优，却并不能保证其在PRC中也是占优的（即PRC占优可以推出该算法在ROC中也占优，而ROC中占优不代表其在PRC中占优）

2.2 ROC与CC（cost curves）之间的关系

如果不同类别中样本个数存在较大的偏差，则ROC曲线可能对算法的性能过分的乐观。Drummond等人推荐使用CC来替代ROC进行算法评价

2.3 AUC的探讨

参考文献：

1. [ROC绘制] .introduction-to-auc-and-roc
2. [F1] wiki.F1_score
3. [ROC] J. A. Hanley and B. J. McNeil. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology, 1982.
4. [ROC] Hanley J A, McNeil B J. A method of comparing the areas under receiver operating characteristic curves derived from the same cases[J]. Radiology, 1983, 148(3): 839-843.
5. [ROC] McNeil B J, Hanley J A. Statistical approaches to the analysis of receiver operating characteristic (ROC) curves[J]. Medical decision making, 1984, 4(2): 137-150.
6. [ROC] DeLong E R, DeLong D M, Clarke-Pearson D L. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach[J]. Biometrics, 1988: 837-845.
7. [ROC] Bradley, A. (1997). The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognition, 30, 1145{1159.
8. [ACC&ROC] Provost, F., Fawcett, T., & Kohavi, R. (1998). The case against accuracy estimation for comparing induction algorithms. Proceeding of the 15th International Conference on Machine Learning (pp. 445{453). Morgan Kaufmann, San Francisco, CA.
9. [ROC&CC] Chris Drummond and Robert C. Holte, ‘Explicitly representing expected cost: An alternative to roc representation’, in Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 198–207, (2000).
10. [ROC] wiki.Receiver_operating_characteristic
11. [AUC] Cortes, C., & Mohri, M. (2003). AUC optimization vs. error rate minimization. Neural Information Processing Systems 15 (NIPS). MIT Press
12. [ROC&CC] Drummond, C., & Holte, R. C. (2004). What ROC curves can't do (and cost curves can). ROCAI (pp. 19{26).
13. [ROC] Zhang, Jun; Mueller, Shane T. (2005). "A note on ROC analysis and non-parametric estimate of sensitivity". Psychometrika. 70: 203–212.
14. [ROC] Fan J, Upadhye S, Worster A. Understanding receiver operating characteristic (ROC) curves[J]. Canadian Journal of Emergency Medicine, 2006, 8(1): 19-20.
15. [ROC] Fawcett, Tom (2006). An Introduction to ROC Analysis. Pattern Recognition Letters. 27 (8): 861–874.
16. [PR&ROC] .The Relationship Between Precision-Recall and ROC Curves, Jesse Davis and Mark Goadrich, ICML 2006
17. [ROC] Brown C D, Davis H T. Receiver operating characteristics curves and related decision measures: A tutorial[J]. Chemometrics and Intelligent Laboratory Systems, 2006, 80(1): 24-38.
18. [ROC] Weng C G, Poon J. A new evaluation measure for imbalanced datasets[C]//Proceedings of the 7th Australasian Data Mining Conference-Volume 87. Australian Computer Society, Inc., 2008: 27-32.
19. [ROC] Powers, David M W (2011). Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation . Journal of Machine Learning Technologies. 2 (1): 37–63.
20. [ROC] Flach P A. ROC analysis[M]//Encyclopedia of machine learning. Springer US, 2011: 869-875.
21. [ROC] Hernandez-Orallo, J. (2013). "ROC curves for regression". Pattern Recognition. 46 (12): 3395–3411 .
22. [ROC] .Using the Receiver Operating Characteristic (ROC) curve to analyze a classification model: A final note of historical interest. Department of Mathematics, University of Utah. Department of Mathematics, University of Utah. Retrieved May 25, 2017.
23. [CC] Drummond C, Holte R C. Cost curves: An improved method for visualizing classifier performance[J]. Machine learning, 2006, 65(1): 95-130.