人们通常先在线性表尾部临时添加一个_数据结构学习笔记-线性表
我们经常会处理一系列类型相同的数据, 创建这种元素组, 读取和修改
当我们处理一个具有有穷或者无穷的元素数据集的时候, 我们需要将其作为一个整体来管理和使用, 用变量去表示它们, 传入和传出函数等等. 因此需要用一种抽象的数据类型去管理它们.
- 从实现者的角度, 需要提供一种有用而且效率高的操作, 来访问和修改这些数据. 为了实现这一目的, 必须把线性表这种数据结构组织好, 赋予一种合适的表示.
- 从使用者的角度, 能简单地去使用这种结构, 有效地实现常用的操作.
结合计算机内存的特点, 重要操作的效率, 人们提出了两种基本的实现模型
- 顺序表: 将数据按顺序连续地放在储存区里, 元素的位置关系由顺序隐式地指出
- 链表:通过链接结构将数据放在分散的位置, 元素的位置由上下文得出
顺序表的实现
设有一个顺序表, 起始的内存位置为
通常为了描述顺序表这个对象的属性, 还会赋予一块记录表属性的信息记录域, 储存最大元素容量和当前元素数.
顺序表的优缺点
- 优点: 按索引访问元素
, 储存紧凑节省空间
- 缺点: 固定大小的元素储存空间会造成内存的浪费. 插入元素的时候会移动许多元素, 效率低
顺序表得基本操作及复杂度
创建空表:
简单判断:
访问元素:
遍历操作:
查找元素:
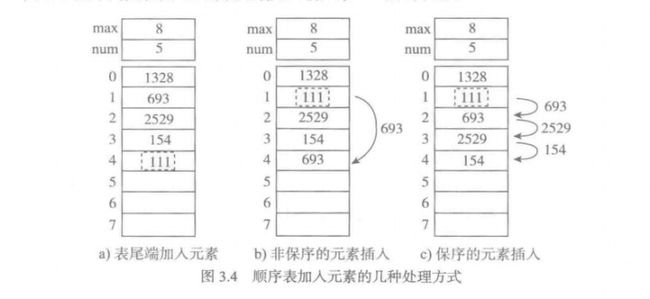
插入元素: 分情况讨论.:从表尾端插入, 非保序的插入, 保序的插入
- 尾端插入:
显然效率最高, 不需要对其他数据进行调整, 只需要保证不越界即可
- 非保序插入:
将插入位置处的数据挪到队尾, 新数据插入
- 保序插入:
调整其后所有元素的位置, 平均来看和数量成正比
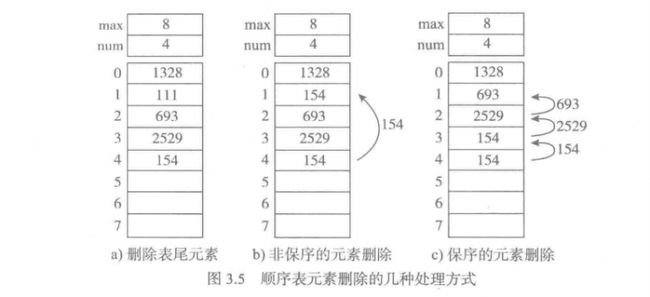
删除元素: 同样三种情况: 删除表尾, 非保序删除, 保序删除
- 特例是查询删除, 这种情况同样也是线性复杂度
动态表的实现
python中的list是动态顺序表, 面对现有的储存空间不够用的情况时采取一下策略:
- 申请更大的元素储存区
- 把现有元素复制到新空间
- 改变信息储存区对元素储存区的链接(指向)
- 加入新元素
我们可以发现一个问题, 即新申请的空间有多大. 采取翻倍增加空间, 则会将复杂度降到
python 顺序表基本操作
- 共有操作
x in s 如果有返回True, 反之False
s1 + s2 两列表合并
s * n n个s合并
s[ : : ] 切片操作
s.index(x[,i [, j ]]) 返回元素x的索引, 可以是在i之后和j之前
s.count(x) 返回x在list中的个数
len() 返回元素个数
max() 返回最大值
min() 返回最小值- 可变列表list
s[i] = x 赋值
s[i:j] = t 将可迭代对象赋值给切片
del s[i:j] 删除 等价于 s[i:j] = []
s.append(x) 尾端添加 等价于 s[len(s):len(s)] = [x] 等价于 s.insert(len(s),x)
s.insert(i,x) 位置i处插入x
s.clear() 清空 等价于 del s[:]
s.extend(t) 列表相加 等价于 s+=t
s.pop([,i]) 弹出 从s中删除最后一个,也可以是指定索引的元素, 并返回
s.remove(x) 移除指定元素
s.reverse() 反转序列 链表--单链表
所谓线性表, 就是元素的序列, 维持这元素间的线性关系, 满足能找到首元素, 从任意元素出发能找到其后的元素. 当需要将数据离散储存的时候, 我们就需要引入链表的概念. 链表中没有显式的前后关联, 但通过链接技术, 能实现元素之间的顺序关系. 基本想法是:
- 把元素储存在独立的储存块中--称为结点
- 从任意结点可以找到下一个结点
- 用链接的方式显示地记录与下一结点之间的关联
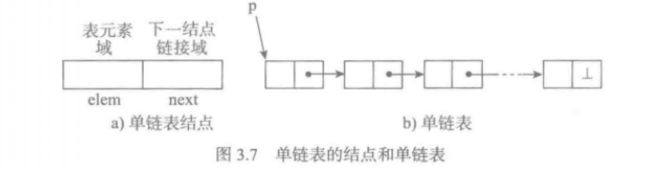
单链表
单链表的结点是一个二元组, 其表元素域elem中保存着数据项, 链接域next中保存着下一个节点的标识. 这样, 从表中任意节点开始都可以找到保存着下一个元素的结点, 即从首结点P出发能找到任何一个结点.
为了表示一个链表的开始, 只需要一个变量保存表得首结点的引用, 把这样的变量成为表头变量或者表头指针. 为了表示一个链表的结束, 只需要给链接域一个空链接, python中可以用None来表示.
基本操作
创建空列表: 只需要把相应的表头变量设置为空链接
删除列表: python中只需要将表指针赋为None, 就抛弃了所有节点, GC会自动回收储存
判断是否为空: 检查表头链接是否为None
判断是否满: 除非储存用完了所有储存空间, 否则不会满
加入元素: 创建一个新结点并存入数据; 将上一个链接指向新结点; 将新结点的链接指向下一个结点.
删除元素: 将上一结点的链接越过待删除的, 直接指向下下个结点.
由于链表的顺序隐式地有链接指明, 因此所有的查询读取操作都是需要对链表进行遍历, 时间复杂度为
循环列表则是将单链表的尾端空链接指向表头链接, 由此可以达成循环的目的.
双列表则是一个储存单元前后各有一个链接, 可以找到上一个和下一个结点