MPC

前言

  本章遵循的一般控制结构是一种级联控制方法，其中一个可靠的适用于系统的低级控制器作为内环，基于模型的轨迹跟踪控制器作为外环运行。

1. 背景 Background

1.1 滚动时域控制 Receding Horizon Control

  滚动时域控制(Receding Horizon Control, RHC)对应着控制理论的历史性发展，该理论旨在解决固定时域控制（fixed horizon control）的已知挑战。固定时域优化在时域的目的是计算未来$N$步的控制输入$\{u_0,u_1,...,u_{N-1}\}$。但是他有两个缺点：

• (a) 当控制设计阶段出现意外(未知)扰动，或控制模型与实际系统行为不同时，控制器无法对计算出的控制序列进行解释；
• (b) 在控制序列的最后一步时，由于剩下的时间较少，不能对目标函数进行求解。

为了解决这些限制，RHC提出了计算整个控制序列后，只应用它第一步的结果，然后再次迭代整个过程(滚动时域的方式)求解新的控制序列。RHC策略一般适用于非线性动力学(考虑到状态更新可用):
$$\dot{x}=f(x,u)(1)$$
其中向量$f:{\mathbb{R}}^n\times {\mathbb{R}}^m$，$x\in {\mathbb{R}}^{n\times 1}$表示状态向量，$u\in {\mathbb{R}}^{m\times 1}$表示输入向量。通常，RHC的基于状态反馈的优化问题可以定义如下。
$$\begin{gathered} \begin{array}{rl}& \underset{z}{\min }F(x_{t+N})+\sum _{k=0}^{N-1}{\Vert x_{t+k}-x_{t+k}^{ref}\Vert }_{\ell }+{\Vert u_{t+k}\Vert }_{\ell }\\ & s.t.\end{array} \\ \begin{array}{rl}{x}_{t+k+1}=f(x_{t+k},u_{t+k})& \\ u_{t+k}\in {\mathfrak{U}}_C& \\ x_{t+k}\in {\mathfrak{X}}_C& \\ x_t=x(t)& \end{array}(2) \end{gathered}$$
其中$z=\{u_t,u_{t+1},......u_{t+N-1}\}$是优化变量，$\ell$表示用于每级的权重(惩罚的度量)，$F(x_{t+N})$表示最终状态的权重，$x_{t+k}^{ref}$表示参考信号，下标$t+k$表示一个信号在当前时间$t$之后$k$步处的采样(使用固定的采样时间$T_s$)，而$t+k+1$则是其下一步的变化，${\mathfrak{U}}_C$表示输入约束集，${\mathfrak{X}}_C$表示状态约束集，$x(t)$是当前RHC迭代开始时的状态向量的值。这个优化问题的解也是一个最优控制序列$\{u_t^{\ast },u_{t+1}^{\ast },......u_{t+N-1}^{\ast }\}$，只使用第一步的控制量$x_t^{\ast }$作为当前的输入，第二步的输入需要再次迭代后获取（白话：每次求解都可以获得一系列包含未来$N$步的最优控制输入，但是实际使用的时候只取第一个，后面的舍弃）。

  在公式1中，$F(x_{t+N})$在闭环稳定中起到了至关重要的作用。它迫使系统状态在预测期结束时在一个特定的集合内取值，可以使用李亚普诺夫稳定性来分析、证明每次局部迭代的稳定性。例如对于一个监管问题（$x_{t+k}^{ref}=0fork=0,...,N-1$），和一个“衰减”因子$\ell$。上述优化问题的解使得系统在$x_t=0$, $u_t=0$处稳定，也就意味着系统的终端约束 （terminal constraint）为 $x_{t+k}=0$，如图1所示。然而，全局的稳定性是没有保证的。为此，必须考虑引入terminal cost和terminal constraint。 但是，仅添加terminal constraints可能不可行，而且一般添加约束的优化问题可能会很难解决。 在许多实际情况下，在控制设计过程中不强制执行terminal constraints，而是验证了后验（如果不满足的话，则可以增加预测范围）。

图1 llustration of the terminal constraint set(Ω)

  此外，RHC的最大挑战就是递归可行性。尽管从理论角度绝对推荐，但由于理论或实践的影响，并不能确保可以构建预先保证递归可行性的RHC。一般来说，RHC策略缺乏递归可行性，因此即使有可能找到可行的状态，但最优控制动作将状态向量移动到RHC优化问题不可行的点。虽然一般的可行性分析方法是非常具有挑战性的，但对于特定的情况可能存在强大的工具可以用来求解。例如对于线性系统，可以使用Farkas的引理与双层编程（bilevel programming）结合来搜索缺乏递归可行性的有问题的初始状态。

1.2 线性模型预测控制 Linear Model Predictive Control

  在本小节中，我们简要介绍了线性系统MPC背后的理论。 给出了输入变量和状态变量均为线性约束的线性系统的最优控制问题。此外，我们还讨论了线性和二次成本函数情况下的控制输入特性，稳定性和可行性。 为了在考虑干扰的情况下实现无偏移跟踪，我们在系统模型中增加了额外的干扰状态$d(t)$来表示模型的误差。 利用观测器（observer）对稳态下的扰动进行估计。本小节将简要讨论观测器的设计和干扰模型。

$$\begin{array}{rl}\min & J_0(x_0,U,X^{ref},U^{ref})\\ \text{subject to }& x_{k+1}=A{x}_k+B{u}_k+B_d{d}_k;\\ & d_{k+1}=d_k,k=0,\dots ,N-1\\ & x_k\in {\mathfrak{X}}_C,u_k\in {\mathfrak{U}}_C\\ & x_N\in {\mathfrak{X}}_{CN}\\ & x_0=x(t_0),d_0=d(t_0)\end{array}(3)$$

  在线性状态和输入约束下实现无偏置状态跟踪的最优控制问题如公式3所示，其中$J_0$是代价函数，$X^{ref}=\{x_0^{ref},\cdots ,x_N^{ref}\}$是参考状态序列，$U^{ref}=\{u_0^{ref},\cdots ,u_{N-1}\}$和$U^{ref}=\{u_0^{ref},\cdots ,u_{N-1}^{ref}\}$分别是控制输入序列和稳态输入序列，$B_d$是扰动模型，$d_k$是外部干扰，${\mathfrak{X}}_C、{\mathfrak{U}}_C$和${\mathfrak{X}}_{CN}$是正多面体（polyhedra）。扰动模型的选择不是一项简单的任务，它取决于所考虑的系统和预期扰动的类型。优化问题定义为

$$\begin{array}{rl}{J}_0(x_0,U,X^{ref},U^{ref})& =\sum _{k=0}^{N-1}\left(\begin{array}{rl}& {(x_k-x_k^{ref})}^T{Q}_x(x_k-x_k^{ref})\\ & +{(u_k-u_k^{ref})}^T{R}_u(u_k-u_k^{ref})\\ & +{(u_k-u_{k-1}^{})}^T{R}_{\Delta }(u_k-u_{k-1}^{})\end{array}\right)\\ & +{(x_N-x_N^{ref})}^{T}P(x_N-x_N^{ref})\end{array}(4)$$

其中$Q_x⪰0$是对状态错误的惩罚，$R_u⪰0$是对控制输入的惩罚，$R_{\Delta }⪰0$是对控制变化率的惩罚，$P$是对终端状态误差的惩罚。

  一般而言，除了一些特殊情况而言，其稳定性和可行性难以保证，例如二次调节器的无限时域控制问题(Linear Quadratic Regulator, LQR)。当预测的步长为$N$步时，其稳定性和可行性保证是值得商榷的。理论上，随和预测步长的增加，有利于提高控制器的稳定性和可行性，但计算量会随之增加，而对于空中机器人应用来说，需要在计算能力有限的平台上进行计算，并对机器人进行快速控制。可以通过选择终端代价$P$和终端约束${\mathfrak{X}}_{CN}$来确保闭环的稳定性和可能性。在本章中，我们更多的关注终端权值P的选择，因为它比较容易计算，而终端约束通常比较困难，其在有足够长的预测范围的情况下可以实现实际的稳定性。

  注意，为了保证输入的平滑、避免不必要的震荡，在成本函数(4)中控制输入率$\Delta u_k$。在成本函数中
(4)，$u_{-1}$为上一个时间步长应用于系统的实际控制输入。

  如前所述，通过对系统模型加入扰动$d_k$来捕获建模误差，可以实现无偏置参考跟踪（offset-free reference tracking）。假设我们想跟踪系统输出$y_k=C{x}_k$，实现稳态偏移无偏置追踪$y_{\infty }=r_{\infty }$。可以用下面这个简单的观察者来估计这种干扰

$$\left[\begin{array}{c}{\hat{x}}_{k+1}\\ {\hat{d}}_{k+1}\end{array}\right]=\left[\begin{array}{cc}A& B_d\\ 0& I\end{array}\right]\left[\begin{array}{c}{\hat{x}}_k\\ {\hat{d}}_k\end{array}\right]+\left[\begin{array}{c}B\\ 0\end{array}\right]u_k+\left[\begin{array}{c}{L}_x\\ L_d\end{array}\right](C{\hat{x}}_k-y_{m,k})(5)$$

其中$\hat{x}$和$\hat{d}$分别是状态和外部干扰的预估，$L_x$和$L_d$是观测器增益，$y_{m,k}$是时间$k$时的测量输出。

  在稳定观测器的假设下，通过求解以下线性方程组，可以计算出在稳定状态$x^{ref}$和稳定状态时输入$u^{ref}$的状态：
$$\left[\begin{array}{cc}A-1& B\\ C& 0\end{array}\right]\left[\begin{array}{c}{x}^{ref,k}\\ u^{ref,k}\end{array}\right]=\left[\begin{array}{c}-B_d{\hat{d}}_k\\ r_k\end{array}\right](6)$$

1.3 非线性模型预测控制 Nonlinear Model Predictive Control

  飞行器的行为可以用一组非线性微分方程来更好地描述，以便更好的捕捉空气动力和耦合效应。因此，在本小节中，我们将介绍非线性MPC背后的理论，其涉及整个系统动力学，并且在轨迹追踪方面表现出更好的效果。非线性MPC的优化问题如式(7)所示。

$$\begin{array}{rl}& \min {\int }_{t=0}^T{{\Vert h\left(x(t),u(t)\right)-y^{ref}(t)\Vert }_Q^{2}dt+\Vert m\left(x(T)\right)-y^{ref}(T)\Vert }_P^2\\ & \begin{array}{rl}\text{s}\text{.t}\text{.}& \dot{x}=f\left(x(t),u(t)\right);\\ & u(t)\in {\mathfrak{U}}_C\\ & x(t)\in {\mathfrak{X}}_C\\ & x(0)=x(t_0).\end{array}\end{array}(7)$$

  多重映射技术(multiple shooting technique)可以用来解决最优控制问题(Optimal Control Problem, OCP)。在这种方法中，系统动力学通过时间网格$t_0,\cdots ,t_N$进行离散化处理。不等式约束和控制动作在同一时间网格上离散化。在每次迭代中求解一个附加的连续性约束的边值问题(Boundary Value Problem, BVP)。由于系统动力学的性质和施加的约束，优化问题成为一个非线性程序(NLP)。该问题的求解采用序列二次规划(Sequential Quadratic Programming, SQP)技术，其中二次规划(Quadratic Programs, QPs)的求解采用主动集方法，使用qpOASES求解器。

1.4 线性鲁棒模型预测控制 Linear Robust Model Predictive Control

  尽管MPC公式具有鲁棒性，但是存在存在鲁棒控制变量时需要进一步的鲁棒性保证。线性鲁棒模型预测控制(Robust Model Predictive Control, RMPC)问题可以表述为一个明确求解的极大极小优化问题。作为一个最优度量，我们可以选择最小峰值性能度量(MPPM)的已知鲁棒性。图2概述了相关的构建块。

图2 Overview of the explicit RMPC optimization problem functional components

  在这种RMPC方法中，可以考虑以下系统动力学的线性时不变表示:

$$\begin{array}{rl}& x_{k+1}=A{x}_k+B{u}_k+G{w}_k\\ & y_{k+1}=C{x}_k\end{array}(8)$$
其中$x_k\in X$、$u_k\in U$干扰$w_k\in W$是已知且有界的。本文中考虑有界的干扰($W_{\infty }=\{w:||x|{|}_{\infty }\le 1\}$)。因此，针对上述的系统和外加干扰，可以定义成RMPC问题。下面表示所预测的输出、状态、输入和干扰的串联版本，其中$[k+i|k]$表示从时间$k$开始的时间$k+i$的值。
$$\mathcal{Y}=(y_{k|k}^T{y}_{k+1|k}^T\cdots y_{k+N-1|k}^T)(9)$$
$$\mathcal{X}=(x_{k|k}^T{x}_{k+1|k}^T\cdots x_{k+N-1|k}^T)(10)$$
$$\mathcal{U}=(u_{k|k}^T{u}_{k+1|k}^T\cdots u_{k+N-1|k}^T)(11)$$
$$\mathcal{W}=(w_{k|k}^T{w}_{k+1|k}^T\cdots w_{k+N-1|k}^T)(12)$$
其中$\mathcal{X}\in {\mathbb{X}}^N=X\times X\cdots \times X$，$\mathcal{U}\in {\mathbb{U}}^N=U\times U\cdots \times U$，$\mathcal{W}\in {\mathbb{W}}^N=W\times W\cdots \times W$。预测的状态和输出与当前状态、未来的控制输入和干扰呈线性相关，因此如下所示:
$$\begin{array}{rl}& \mathcal{X}=\mathcal{A}{x}_{k|k}+\mathcal{B}\mathcal{U}+\mathcal{G}\mathcal{W}\\ & \mathcal{Y}=\mathcal{C}\mathcal{X}\end{array}(13)$$
其中$\mathcal{A}$、$\mathcal{B}$、$\mathcal{C}$和$\mathcal{G}$是堆叠的状态向量矩阵。因此，基于MPPM的RMPC问题(MPPM - RMPC)可表述为:
$$\begin{array}{rl}\underset{u}{\min }\underset{w}{\max }& {\Vert Y\Vert }_{\infty },{\Vert Y\Vert }_{\infty }=\max {\Vert y_{k+j|k}\Vert }_{\infty }\\ \text{subject to }& u_{k+j|k}\in U,\forall w\in W\\ & x_{k+j|k}\in X,\forall w\in W\\ & w_{k+j|k}\in W\end{array}(14)$$

1.4.1 反馈预测 Feedback Predictions

  按照上述公式，优化问题将趋于保守，因为优化本质上计算的是开环控制序列。反馈预测是一种对遵循后退时域方法的知识进行编码的方法。为了将它们合并，必须假定一种反馈控制结构。在已知导致凸问题空间的反馈参数化中，选择如下:

1.4.2 鲁棒不确定不等式 Robust Uncertain Inequalities Satisfaction

2. 用于多旋翼系统的基于模型的轨迹跟踪控制器 Model-Based Trajectory Tracking Controller for Multi-rotor System

  在本节中，我们提出一个多转子系统的简化模型，可用于基于模型的控制来实现轨迹跟踪，并提出一个线性和非线性的模型预测控制器来实现轨迹跟踪。

2.1 多旋翼系统模型 Multirotor System Model

  多旋翼系统的6DoF位姿可以通过固定惯性坐标系$W$（世界坐标系）和机身坐标系$B$来定义，如图3所示。我们用$p$表示坐标系$W$中坐标系$B$的原点位置，用$R$表示坐标系$W$中坐标系$B$的旋转矩阵。此外，我们用$\phi$、$\theta$和$\psi$来表示飞行器的横摇、俯仰和偏航角。在该模型中，我们假设一个低级的姿态控制器能够跟踪期望的横摇和俯仰${\phi }_d$、${\theta }_d$角，并具有一阶行为。一阶内环近似为MPC提供了充分的信息来考虑低电平控制器的行为。通过经典的系统辨识技术，可以辨识出回路的一阶参数。用于多转子系统轨迹跟踪的非线性模型如式(37)所示。

图3 Illustration of the Firefly hexacopter from Ascending Technologies with attached body fixed frame B and inertial frame W

$$\begin{array}{rl}& \dot{p}(t)=v(t)\\ & \dot{v}(t)=R(\psi ,\theta ,\varphi )\left(\begin{array}{c}0\\ 0\\ T\end{array}\right)+\left(\begin{array}{c}0\\ 0\\ -g\end{array}\right)-\left(\begin{array}{ccc}{A}_x& 0& 0\\ 0& A_y& 0\\ 0& 0& A_z\end{array}\right)v(t)+d(t)\\ & \dot{\varphi }(t)=\frac{1}{{\tau }_{\varphi }}\left(K_{\varphi }{\varphi }_d(t)-\varphi (t)\right)\\ & \dot{\theta }(t)=\frac{1}{{\tau }_{\theta }}\left(K_{\theta }{\theta }_d(t)-\theta (t)\right)\end{array}(37)$$
其中$v$代表无人机的速度，$g$是重力加速度，$T$是质量标准化推力，$A_x$、$A_y$和$A_z$表示质量归一化阻力系数，$d$是外部干扰，${\tau }_{\phi }$、$K_{\phi }$和${\tau }_{\theta }$、$K_{\theta }$分别为滚转角和俯仰角内环行为的时间常数和增益。

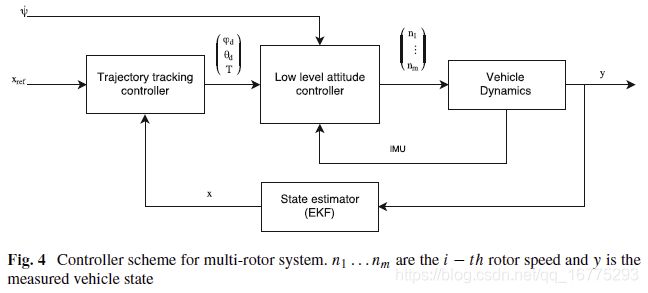
  本章假设的级联控制器结构如图4所示。

图4 Controller scheme for multi-rotor system. n1 . . . nm are the i − th rotor speed and y is the measured vehicle state

2.2 Linear MPC

  在本小节中，我们将展示如何制定一个线性MPC来实现多旋翼系统的轨迹跟踪，并将其集成到ROS中。利用CVXGEN框架生成c代码求解器，求解式(3)中的优化问题。CVXGEN利用问题结构生成了一个求解凸优化问题的高速求解器。为了清晰起见，我们在这里重写了优化问题，并展示了如何使用CVXGEN生成自定义求解器。优化问题定义如下：

$$\begin{array}{rl}\underset{u}{\min }& \sum _{k=0}^{N-1}\left(\begin{array}{rl}& {(x_k-x_k^{ref})}^T{Q}_x(x_k-x_k^{ref})\\ & +{(u_k-u_k^{ref})}^T{R}_u(u_k-u_k^{ref})\\ & +{(u_k-u_{k-1}^{})}^T{R}_{\Delta }(u_k-u_{k-1}^{})\end{array}\right)+{(x_N-x_N^{ref})}^{T}P(x_N-x_N^{ref})\\ \text{subject to}& x_{k+1}=A{x}_k+B{u}_k+B_d{d}_k；\\ & d_{k+1}=d_k,k=0,\dots ,N-1\\ & u_k\in {\mathfrak{U}}_C\\ & x_0=x(t_0),d_0=d(t_0)\end{array}(38)$$

为生成上述优化问题的求解器，CVXGEN中使用了以下问题描述。

dimensions
  m = 3 # dimension of i n p u t s .
  nd = 3 # dimension of d i s t u r b a n c e s .
  nx = 8 # dimension of s t a t e ve c t o r .
  T = 18 # horizon − 1 .
  end
 
  parameters
  A (nx,nx) # dynamics mat r ix .
  B (nx,m) # t r a n s f e r matrix .
  Bd ( nx , nd ) # di s t u r b a n c e t r a n s f e r mat r ix
  Q_x ( nx , nx ) psd # s t a t e cost , p o s i t i v e semidi f ined .
  P (nx,nx) psd # f i n a l s t a t e penal ty , p o s i t i v e semidi f ined .
  R_u (m,m) psd # input penal ty , p o s i t i v e semidi f ined .
  R_delta (m,m) psd # de l t a input penal ty , p o s i t i v e semidi f ined .
  x [0] ( nx ) # i n i t i a l s t a t e .
  d (nd) # di s t u r b a n c e s .
  u_prev (m) # previous input applied to the system .
  u_max (m) # input ampl i tude l i m i t .
  u_min (m) # input ampl i tude l i m i t .
  x_ss [ t ] ( nx ) , t =0. .T+1 # r e f e r e n c e s t a t e .
  u_ss [ t ] (m) , t =0. .T # r e f e r enc e input .
end

variables
  x [ t ] ( nx ) , t =1. .T+1 # s t a t e .
  u [ t ] (m) , t =0. .T # input .
  end
 
  minimize
  quad ( x[0]−x_ss [0] , Q_x) + quad ( u[0]−u_ss [0] , R_u) + quad ( u [0] −
u_prev , R_del ta ) + sum[ t =1 . .T] ( quad ( x [ t ]−x_ss [ t ] , Q_x) + quad (
u [ t ]−u_ss [ t ] , R_u) + quad ( u [ t ] − u [ t −1] , R_delta ) )+quad ( x [T+1]−
x_ss [T+1] , P)
  s u b j e c t to
  x [ t +1] == A∗x [ t ] + B∗u [ t ] + Bd∗d , t=0..T # dynamics
  u_min <= u [ t ] <= u_max , t = 0 . .T # input c o n s t r a i n t .
end

  在将生成的求解器集成到ROS中之前，我们讨论了如何估计姿态环参数${\tau }_{\phi }$，$K_{\phi }$，${\tau }_{\theta }$，$K_{\theta }$，以及离散系统模型A,B,Bd的推导。

3.2.1 姿态环参数辨识 Attitude Loop Parameters Identification

  如果不了解无人机上上使用的姿态控制器，则建议进行姿态环识别。 许多市售平台就是这种情况。 姿态命令和实际无人机姿态（使用运动捕捉系统（如果可用）或惯性测量单元（IMU）估算）均带有准确的时间戳记。 通常收集两个数据集，一个用于参数估计，另一个用于验证目的。

  要使用可用脚本进行参数识别，请遵循以下步骤:

1. 准备系统，并确保您能够记录带时间戳的姿态命令和实际无人机姿态。
2. 执行飞行，将命令和无人机姿态记录在包文件中。 在飞行过程中，尽可能的激活无人机的每个轴。
3. 重复飞行测试以收集验证数据集。
4. 在提供的脚本中设置正确的包文件名和主题名称，然后运行它。
5. 控制器参数将以确认百分比显示在屏幕上，以确认标识的有效性。

3.2.2 线性化、解耦和离散化 Linearization, Decoupling and Discretization

  在设计控制器时，可以假定无人机以小姿态角、飞行器航向与惯性坐标系x轴对齐(即$\psi =0$)的情况下，这时可以近似计算悬停状态下的飞行器动力学。围绕悬停状态的线性化方程组可以写成

$$\dot{x}(t)=\left(\begin{array}{rlrlrlrl}0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& -Ax& 0& 0& g& 0\\ 0& 0& 0& 0& -Ay& 0& 0& -g\\ 0& 0& 0& 0& 0& -Az& 0& 0\\ 0& 0& 0& 0& 0& 0& -\frac{1}{{\tau }_{\varphi }}& 0\\ 0& 0& 0& 0& 0& 0& 0& -\frac{1}{{\tau }_{\theta }}\end{array}\right)x(t)+\left(\begin{array}{rlr}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ \frac{K_{\varphi }}{\tau \varphi }& 0& 0\\ 0& \frac{K_{\theta }}{{\tau }_{\theta }}& 0\end{array}\right)u(t)+\left(\begin{array}{rlr}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)d(t)(39)$$
其中状态向量$x=\{p^T,v^T,{}^W\varphi ,{}^W\theta {\}}^T$，输入向量$u=\{{}^W{\varphi }_d,{}^W{\theta }_d,T{\}}^T$，干扰向量$d=(d_x,d_y,d_z{)}^T$。公式（38）中三个矩阵分别对应连续时间模型中的$A_c$、$B_c$和$B_{d,c}$。注意，在这个线性化中，我们将姿态标记为在惯性坐标系$W$，以消除模型中的偏航角$\psi$。在惯性坐标系中计算姿态控制动作$W_{{\phi }_d}$、$W_{{\theta }_d}$，然后绕$z$轴旋转将姿态控制动作转化为机体框架。机体框架$B$中的控制作用为

$$\left(\begin{array}{c}{\varphi }_d\\ {\theta }_d\end{array}\right)\text{=}\left(\begin{array}{cc}\cos \psi & \sin \psi \\ -\sin \psi & \cos \psi \end{array}\right)\left(\begin{array}{c}{}^W{\varphi }_d\\ {}^W{\theta }_d\end{array}\right)(40)$$

  在计算控制输入后，建议加入前馈项来补偿耦合效应，以获得更好的跟踪性能。为了补偿非零姿态对推力的影响，实现更好的动态轨迹跟踪，采用了以下补偿方案。

$$\begin{array}{rl}& \tilde{T}\text{=}\frac{T+g}{\cos \varphi \cos \theta }+{}^B{\ddot{z}}_d\\ & {\tilde{\varphi }}_d\text{=}\frac{g{\varphi }_d-{}^B{\ddot{y}}_d}{\tilde{T}}\\ & {\tilde{\theta }}_d\text{=}\frac{g{\theta }_d+{}^B{\ddot{x}}_d}{\tilde{T}}\end{array}(41)$$
其中${}^B{\ddot{x}}_d$、${}^B{\ddot{y}}_d$和${}^B{\ddot{z}}_d$是机体坐标系下期望轨迹加速度，带波浪符号的量是实际应用的控制输入。

  由于控制器是在离散时间内实现的，因此有必要对系统动力学进行离散化(39)。这可以如下所示
$$\begin{array}{rl}& A=e^{A_c{T}_s}\\ & B={\int }_0^{T_s}{e}^{A_c\tau }d\tau B_c\\ & B_d={\int }_0^{T_s}{e}^{A_c\tau }d\tau B_{d,c}\end{array}(42)$$
其中$T_s$为采样时间。终端代价$P$矩阵的计算是通过迭代求解代数Riccati方程来完成的。

2.2.3 ROS集成 ROS Integration

  在ROS中集成求解器时，通常需要创建一个ROS节点来将控制器连接到ROS环境，而控制器、估计器和其他组件实现为c++共享库，在编译时链接到节点。控制器节点将无人机状态作为nav里程计消息，并封装成自定义消息类型RollPitchYawRateThrust。规划出的轨迹可以发送到ROS主题MultiDOFJointTrajectory上，也可以作为单个PoseStamped类型的轨迹点。将整个预期轨迹传递给单个点的优势在于，MPC可以考虑未来的预期轨迹并做出相应的反应。图5通过ros图概述了节点和话题之间的通信关系。

图5 ROS graph diagram showing various nodes and topics to control multi-rotor system

  控制器每次接收到新的里程计消息时，就计算并发布一个控制动作。因此，这就需要状态估计器以期望的控制速率发布里程测量信息。我们推荐控制器使用多传感器融合的模块化框架(Modular Framework for MultiSensor Fusion)。在实现这种控制器时，需要尽可能地减少循环中的延迟。例如可以通过ROS:: transporthents()和ros::TransportHints()来发送数据给里程计话题的订阅者。

  控制器节点发送以下消息：

1. Current desired reference as tf.

图6 Through dynamic reconfiguration it is possible to change the controller parameters online for tuning purposes

2. Desired trajectory as rviz marker.
3. Predicted vehicle state as rviz marker.

可以通过修改图6中的参数来动态修改控制器的参数。控制器的开源代码连接为https://github.com/ethz-asl/mav_control_rw.

图7 Aggressive trajectory tracking performance using linear MPC controller running onboard of Firefly hexacopter from Ascending Technologies

2.2.4 实验结果 Experimental Results

为了验证控制器的性能，我们追踪一段轨迹。控制器运行在上Ascending Technologies (AscTec)的一架Firefly六轴无人机上，机载一台NUC i7计算机。采用外部运动捕捉系统Vicon作为姿态传感器，利用多传感器融合框架(MSF)将其与车载仿真系统融合。控制器运行在100Hz，预测的时长为20步。图7展示了控制器的追踪性能。

2.3 Nonlinear MPC

  在本小节中，我们利用无人机的非线性模型设计连续时间非线性模型预测控制器。用于生成非线性求解器的工具包是ACADO，它能够为一般的最优控制问题OCP（optimal control problems）快速生成C语言求解器。优化问题可以写成

$\begin{array}{rl}\underset{U}{\min }& {\int }_{t=0}^T{\left(x(t)-x^{ref}(t)\right)}^T{Q}_x\left(x(t)-x^{ref}(t)\right)+\left(u(t)-u^{ref}(t)\right)R_u\left(u(t)-u^{ref}(t)\right)dt\\ & +\left(x(T)-x^{ref}(T)\right)P\left(x(T)-x^{ref}(T)\right)\\ & \begin{array}{rl}\text{s}\text{.t}\text{.}& \dot{x}=f\left(x,u\right);\\ & u(t)\in {\mathfrak{U}}_C\\ & x(0)=x(t_0).\end{array}\end{array}(43)$

  为了生成上述优化问题的求解器，在ACADO的Matlab界面中使用下面的问题描述。

1 c l c ;
2 c l e a r a l l ;
3 close a l l ;
4
5 Ts = 0 . 1 ; %sampling time
6 EXPORT = 1 ;
7
8 D i f f e r e n t i a l S t a t e p o s i t i o n (3) ve l o c i t y (3) r o l l p i t c h yaw;
9 Control r o l l _ r e f p i t c h _ r e f t h r u s t ;
10
11 %online data r epr e s ent data t h a t can be pa s s ed to the s o l v e r online .
12 OnlineData r o l l _ t a u ;
13 OnlineData r o l l _ g a i n ;
14 OnlineData p i t c h _ t a u ;
15 OnlineData pi t c h _ g a i n ;
16 Onl ineData yaw_rate_command ;
17 OnlineData dr a g _ c o e f f i c i e n t (3) ;
18 OnlineData e x t e r n a l _ d i s t u r b a n c e s (3) ;
19
20 n_XD = length ( d i f f S t a t e s ) ;
21 n_U = length ( c o n t r o l s ) ;
22
23 g = [ 0 ; 0 ; 9 . 8 0 6 6 ] ;
24
25 %% Di f f e r e n t i a l Equation
26
27 %de f ine v e h i c l e body z−axi s expres sed in i n e r t i a l frame .
28 z_axis = [ ( cos (yaw) ∗ s i n ( p i t c h ) ∗cos ( r o l l )+s i n (yaw) ∗ s i n ( rol l ) ) ; . . .
29 ( s i n (yaw) ∗ s i n ( p i t c h ) ∗cos ( r o l l )−cos (yaw) ∗ s i n ( rol l ) ) ; . . .
30 cos ( p i t c h ) ∗cos ( r o l l ) ] ;
31
32 d r o l l = (1/ r o l l _ t a u ) ∗( r o l l _ g a i n ∗ r o l l _ r e f − r o l l ) ;
33 dpitch = (1/ p i t c h _ t a u ) ∗( pi t c h _ g a i n ∗ p i t c h _ r e f − p i t c h ) ;
34
35 f = dot ( [ p o s i t i o n , ve loc i ty ; r o l l ; p i t c h ; yaw] ) == . . .
36 [ ve l o c i t y . . . ;
37 z_axis ∗ t h r u s t − g − diag ( dr a g _ c o e f f i c i e n t ) ∗ v e l o c i t y +
e x t e r n a l _ d i s t u r b a n c e s ; . . .
38 d r o l l ; . . .
39 dpitch ; . . .
40 yaw_rate_command ] ;
41
42 h = [ p o s i t i o n ; ve l o c i t y ; r o l l ; p i t c h ; r o l l _ r e f ; p i t c h _ r e f ; z_axis (3) ∗
t h r u s t −g (3) ] ;
43
44 hN = [ p o s i t i o n ; ve l o c i t y ] ;
45
46
47 %% NMPCexport
48 acadoSet ( ’ problemname ’ , ’ nmpc_trajectory_tracking ’ ) ;
49
50 N = 20;
51 ocp = acado .OCP( 0.0 , N∗Ts , N ) ;
52
53 W_mat = eye ( length ( h ) ) ;
54 WN_mat = eye ( length (hN) ) ;
55 W = acado . BMatrix (W_mat ) ;
56 WN = acado . BMatrix (WN_mat) ;
57
58 ocp . minimizeLSQ ( W, h ) ;
59 ocp . minimizeLSQEndTerm ( WN, hN ) ;
60 ocp . subjectTo(−deg2rad (45) <= [ r o l l _ r e f ; p i t c h _ r e f ] <= deg2rad (45) ) ;
61 ocp . subjectTo ( g (3) /2.0 <= t h r u s t <= g (3) ∗1.5) ;
62 ocp . setModel ( f ) ;
63
64 mpc = acado . OCPexport ( ocp ) ;
65 mpc . s e t ( ’HESSIAN_APPROXIMATION’ , ’GAUSS_NEWTON’ ) ;
66 mpc . s e t ( ’DISCRETIZATION_TYPE ’ , ’MULTIPLE_SHOOTING’ ) ;
67 mpc . s e t ( ’SPARSE_QP_SOLUTION’ , ’FULL_CONDENSING_N2’ ) ;
68 mpc . s e t ( ’INTEGRATOR_TYPE’ , ’INT_IRK_GL4 ’ ) ;
69 mpc . s e t ( ’NUM_INTEGRATOR_STEPS’, N ) ;
70 mpc . s e t ( ’QP_SOLVER’ , ’QP_QPOASES’ ) ;
71 mpc . s e t ( ’HOTSTART_QP’ , ’NO’ ) ;
72 mpc . s e t ( ’LEVENBERG_MARQUARDT’, 1e−10 ) ;
73 mpc . s e t ( ’LINEAR_ALGEBRA_SOLVER’ , ’GAUSS_LU’ ) ;
74 mpc . s e t ( ’IMPLICIT_INTEGRATOR_NUM_ITS’, 4 );
75 mpc . s e t ( ’CG_USE_OPENMP’ , ’YES’ ) ;
76 mpc . s e t ( ’CG_HARDCODE_CONSTRAINT_VALUES’ , ’NO’ ) ;
77 mpc . s e t ( ’CG_USE_VARIABLE_WEIGHTING_MATRIX’ , ’NO’ ) ;
78
79
80
81 i f EXPORT
82 mpc . exportCode ( ’mav_NMPC_trajectory_tracking ’ ) ;
83
84 cd mav_NMPC_trajectory_tracking
85 make_acado_solver ( ’ . . / mav_NMPC_trajectory_tracking ’ )
86 cd . .
87 end

2.3.1 ROS集成 ROS Integration

  非线性控制器的ROS集成遵循先前介绍的线性MPC的相同准则。 可以在此处找到先前介绍的控制器的开源实现 https://github.com/ethz-asl/mav_control_rw。

2.3.2 实验结果 Experimental Results

  非线性MPC的设置方式与线性MPC相同， 唯一的不同是，我们目前正在以更具波动性的（aggressive）轨迹评估控制器，如图8所示。

图8 Aggressive trajectory tracking performance using nonlinear MPC controller running onboard of Firefly hexacopter from Ascending Technologies

3 结论 Conclusion

在这一章中，我们概述了多种类型的无人机基于模型的控制策略。提出了多旋翼系统的鲁棒MPC、多旋翼系统的线性MPC和多旋翼系统及固定翼无人机的非线性MPC策略。这些控制策略在实际实验中进行了评价，本章给出了性能评价。所提出的控制器可作为开放源码ROS包在https://github.com/ethz-asl/mav_control_rw和https:// github.com/ethz-asl/mav_control_fw，前者是多旋翼，后者是固定翼。

原文献

• Kamel, M. , Stastny, T. , Alexis, K. , & Siegwart, R. . (2017). Model Predictive Control for Trajectory Tracking of Unmanned Aerial Vehicles Using Robot Operating System. Robot Operating System (ROS) The Complete Reference, Volume 2. Springer International Publishing.